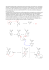Na czym polega metoda obrazów w elektrostatyce?

Na czym polega metoda obrazów w elektrostatyce?
Wyjaśnijmy to na przykładzie zadania
Punktowy ładunek q umieszczono w odległości h od uziemionej, nieskończonej, metalowej płyty. Znajdź potencjał pola w części przestrzeni, w której znajduje się ładunek punktowy.
ROZWIĄZANIE
Z pozoru zadanie jest proste. Z ładunkami punktowymi mieliśmy często do czynienia.
Uczyliśmy się jak rozwiązywać zadania polegające na wyznaczaniu pola, gdy dane są
wszystkie źródła pola. Czy tak jest i w tym zadaniu? Nie! Wiecie , że obecność przewodników, nawet nie naładowanych, w pobliżu źródeł pola, zmienia potencjał i natężenie. Zmiana ta jest spowodowana tym, że ładunki w przewodniku, które pozostawały w idealnej
równowadze, gdy nie było zewnętrznego pola, w jego obecności przemieszczają się i same stają się źródłem dodatkowego pola, które dodaje się do już istniejącego. Kłopot polega na tym, że to dodatkowe źródło pola nie jest znane. Nie wiemy jakie ładunki wyindukują
się na przewodniku, jak będą na nim rozłożone. Oczywiście są metody, by się tego
wszystkiego dowiedzieć, ale nie są one proste. Jedną z nich, jest metoda obrazów. To
zadanie jest pretekstem, by was z nią zapoznać. Nie jest ona aż tak skomplikowana, by
nie była dostępna licealiście, no może nie każdemu.
q
h
Ładunki
wyindukowane
Zaczniemy od uwagi, że skoro płyta jest uziemiona to jej potencjał jest równy zero. Potencjał całej płyty. W jakiej jeszcze sytuacji potencjał jest równy zeru na płaszczyźnie? Przypomnijmy sobie układ jednakowych co do wartości bezwzględnej lecz przeciwnego znaku
ładunków.
Zielona linia jest płaszczyzną symetralną odcinka łączącego ładunki. Jaki jest potencjał na
tej symetralnej? Odległości każdego punktu symetralnej od obu ładunków są jednakowe.
kq
kq
dla
od dodatniego i −
r
r
ujemnego. Całkowity potencjał jest równy zero! Tak jak w naszym zadaniu na płycie. Wobec tego można zastąpić układ ładunek – płyta (z ładunkiem wyindukowanym), układem
ładunek – ładunek do niego przeciwny. Ten drugi ładunek (wyobrażony) jest jak gdyby
obrazem ładunku rzeczywiście istniejącego. Stąd nazwa metody. Naszym zadaniem jest
obliczenie potencjału w półprzestrzeni zawierającej ładunek punktowy. Chyba nie unikniemy wprowadzenia układu współrzędnych. Po to by móc powiedzieć jaki jest potencjał w
różnych punktach przestrzeni musimy umieć je odróżniać, a to najlepiej robić za pomocą
układu współrzędnych.
Zatem potencjały od ładunków na symetralnej wynoszą:
z
P (x,y,z)
r1
z=h
r2
y
x
z=-h
-q
Potencjał w dowolnym punkcie P (x,y,z) jest oczywiście równy
kq kq
V=
−
r1
r2
Dalsze rozwiązanie polega na wyrażeniu r1 i r2 poprzez współrzędne punktu P i h. To proste
2
r12 = x 2 + y 2 + (z − h )
r 22 = x 2 + y 2 + (z + h )
2
r1 = x 2 + y 2 + (z − h )
2
2
r 2 = x 2 + y 2 + (z + h )
Zatem potencjał
kq
kq
V ( x, y , z ) =
−
2
2
x 2 + y 2 + (z − h )
x 2 + y 2 + (z + h )
Przy okazji spróbujcie odpowiedzieć na pytanie: jaka siła działa między ładunkiem punktowym a wyindukowanym ładunkiem na płycie?
A co z potencjałem po drugiej stronie płyty?
A jak zrobić metodą obrazów następujące zadanie?
Punktowy ładunek q umieszczono wewnątrz uziemionego, nieskończonego, metalowego
kąta dwuściennego złożonego z dwóch prostopadłych do siebie płyt. Ładunek znajduje się
w odległościach a i b od płyt. Znajdź potencjał pola w części przestrzeni, w której znajduje
się ładunek punktowy.