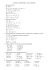TRENING PRZED SPRAWDZIANEM 1.Oblicz: a) 5 1 2: 2 1 16 17 5 4
Transkrypt
TRENING PRZED SPRAWDZIANEM 1.Oblicz: a) 5 1 2: 2 1 16 17 5 4
TRENING PRZED SPRAWDZIANEM
1.Oblicz:
2
3 4
2
3 1
1
1
1 2 3 4
10 2 3 2
2
3
4 5
2
5
4 5
a)
; b)
1 1
1 1
17 16 : 2
33 : 16 : 2
2 5
2 5
2.Dana jest funkcja y = -3x + l.
a) Czy funkcja ta jest rosnąca, czy malejąca?
b) Narysuj wykres tej funkcji.
c) Oblicz miejsce zerowe.
d) Podaj współrzędne punktów przecięcia wykresu funkcji z osiami układu współrzędnych.
e) Dla jakich argumentów funkcja przyjmuje wartości dodatnie?
f) Dla jakich argumentów funkcja przyjmuje wartości ujemne?
g) Oblicz wartość funkcji dla argumentu x = -12.
h) Dla jakiego argumentu funkcja przyjmuje wartość 20?
i) Dla jakich argumentów funkcja przyjmuje wartości mniejsze od -l?
j) Dla jakich argumentów funkcja przyjmuje wartości nie mniejsze od 6?
3. Poniżej podany jest dobowy wykres temperatury.
Odpowiedz na pytania:
a) W jakich godzinach dokonywano pomiaru?
b) W jakim przedziale mieszczą się zanotowane temperatury?
c) W jakich godzinach temperatura wyniosła 0?
d) W jakich godzinach temperatura była dodatnia, a w jakich ujemna?
e) W jakich godzinach temperatura rosła, a w jakich malała?
f) Jaką wartość miała temperatura w godzinach 12, 14?
g) Jaką najniższą wartość wskazał termograf?
4. Wartość podwojonej różnicy kwadratów liczb 13 i 3 wynosi:
A) 8
B) 16
C) 44 12 3
5. Podwojony kwadrat sumy liczb
A) 18 4 5
B) 18
D) 6
5 i 2 ma wartość:
C) 14
D) 18 8 5
6. Iloraz sumy liczb 7 i 2 2 przez ich różnicę ma wartość:
A) 30 8 14
B) 30 8 14
C) 30 8 14
7.Usuń niewymierność z mianownika ułamka:
8. Liczbą odwrotną do liczby
A)
B)
2 3
1 2
D) 30 8 14
.
jest:
C)
D)
1
9. Porównaj liczby 6 5 oraz 6 5 .
10. Cenę produktu zmniejszono o 10%, a potem podwyższono o 10% i wynosi ona 49,50 zł. Jaką
cenę miał produkt przed tymi zmianami?
11. Liczba 6,5 stanowi 175% liczby a. Sprawdź, czy liczba a należy do przedziału (-6; 3 .
12. Rozwiąż nierówność: x 3 2 . Zaznacz zbiór rozwiązań na osi liczbowej,
a następnie wskaż wśród rozwiązań nierówności
a) liczby naturalne
b) najmniejszą liczbę pierwszą
13. Rozwiązanie nierówności x 4 1
A) jest takie samo jak suma rozwiązań dwóch nierówności: x 5 lub x 4 .
B) to przedział <3; 5>
C) to zbiór liczb mniejszych od 5
D) to zbiór liczb większych od 3.
14. Rozwiąż równania i nierówności.
a) x 2 3
b) 5x 3 2
c) x 3 2
e) 3x 3 2
f) x 5
g) x 1 8
d) 10 x 4 0
h) 3 7 x 10
4
15. Liczba 33 3 9 3 27 1,5 jest równa
A) 3
1
2
3
B)
3
1
C)
3
1
2
16. Liczba x jest równa 49, gdy
( 7 )6
A) x =
B) x = 7-6∙492∙73
( 7 ) 2
D)
3
3
75 7 2 6 76
C) x =
74
17. Wyznacz zbiory A B, C D, A – D, jeśli:
A = { –3, –2, –1, 3, 4 }, B = { –2, 0, 1, 3 },
C = –1, 4 , D = ( 0 , 7
18. Wyznacz zbiory A B, A B, A B oraz B A , jeśli:
a/ A 2,1,0,1,5, B 1,3,8
b/ A 1,2,3,4,5, B 5,4,3,2,1
c/ A 5,7,9,11, B 7,9
d/ A 3,4,5, B 3,4,5,6,7
e/ A 1,2,3, B 1,2,3
f/ A 5,3,1,1,3,5, B 1,2,3,4,5
D) x = - 72