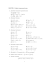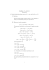1. Na płaszczyźnie zespolonej naszkicować zbiór: z ∈ C : Re 1 ¯z

A
1. Na płaszczyźnie zespolonej naszkicować zbiór:
z ∈ C : Re
1
z̄ − 2i
>1 .
Rozwiązanie: Podstawiając z = x + iy, x, y ∈ R, otrzymujemy:
1
1
1
x + i(y + 2)
x + i(y + 2)
=
=
·
= 2
z̄ − 2i
x − iy − 2i
x − iy − 2i x + i(y + 2)
x + (y + 2)2
Wtedy nierówność Re
1
z̄−2i
> 1 przyjmuje postać
x
> 1,
x2 + (y + 2)2
czyli x > x2 + (y + 2)2 , co po przekształceniach daje x2 − x + (y + 2)2 < 0 i ostatecznie
(x − 12 )2 + (y + 2)2 < 14 . Jest to wnętrze koła o środku 21 − 2i i promieniu 12 .
√
2. Wyznaczyć 3 i (elementy podać w postaci algebraicznej).
Rozwiązanie: i = cos π2 + i sin π2 , więc elementami pierwiastka są:
√
π
3 1
π
+ i
w0 = cos + i sin =
6
6
2
2
√
π
π
+
2π
+
2π
5π
5π
3 1
+ i sin 2
= cos
+ i sin
=−
+ i
w1 = cos 2
3
3
6
6
2
2
π
π
+
4π
+
4π
9π
9π
w2 = cos 2
+ i sin 2
= cos
+ i sin
= −i
3
3
6
6
B
1. Na płaszczyźnie zespolonej naszkicować zbiór:
n
o
z ∈ C : Im z 6 > 0 .
Rozwiązanie: Wykorzystamy postać trygonometryczną: z = r(cos ϕ + i sin ϕ).
Ze
6
6
6
wzoru de Moivre’a mamy wtedy z = r (cos 6ϕ + i sin 6ϕ), a nierówność Im z > 0
sprowadza się do r sin 6ϕ > 0. Ponieważ r = |z| jest nieujemne, mamy warunek
sin 6ϕ > 0, co daje 6ϕ ∈ (0, π), czyli:
π
π π
2π 5π
7π
4π 3π
5π 11π
ϕ ∈ (0, ) ∪ ( , ) ∪ ( , ) ∪ (π, ) ∪ ( , ) ∪ ( ,
).
6
3 2
3 6
6
3 2
3
6
Na rysunku jest to sześć sektorów kątowych o rozpiętości π6 .
√
2. Wyznaczyć 3 8 (elementy podać w postaci algebraicznej).
Rozwiązanie: 8 = 8(cos 0 + i sin 0), więc elementami pierwiastka są:
w0 = 2(cos 0 + i sin 0) = 2
√
2π
2π
w1 = 2 cos
+ i sin
= −1 + i 3
3
3
√
4π
4π
w2 = 2 cos
+ i sin
= −1 − i 3
3
3