Kurs Wybranego Języka Programowania (ADA)

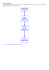
Kurs Wybranego Języka
Programowania (ADA)
Lista 0.5
(podstawy języka)
Przemysław Kobylański
Wstęp
Drzewem binarnym nazywać będziemy strukturę dynamiczną, której każdy węzeł
jest rekordem o dwóch polach zawierających odpowiednio wskazanie na lewe i prawe
poddrzewo. Wskazaniem na drzewo binarne jest wskazanie na węzeł znajdujący się w
jego korzeniu.
Pustym drzewem binarnym jest struktura niezawierająca żadnego węzła i wskazaniem na puste drzewo binarne jest null.
Przykład drzewa binarnego o czterech węzłach:
null
null
null
null
null
Rozpatrzmy następujące trzy sposoby generowania losowych drzew binarnych o
n węzłach:
• początkowo drzewo jest puste a następnie n-krotnie powtarza operację polegającą na wyborze, z jednostajnym prawdopodobieństwem, pola zawierającego
wskazanie null i zastąpieniu go wskazaniem na poddrzewo z dokładnie jednym węzłem, przy czym za każdym razem każde pole zawierające null ma
to samo prawdopodobieństwo wyboru (w przykładowym drzewie są już cztery węzły zawierające łącznie pięć pól ze wskaźnikami null więc pole takie
zacznie wskazywać nowy węzeł z prawdopodobieństwem 1/5).
• początkowo drzewo jest puste a następnie n-krotnie powtarza się operację polegającą na losowym błądzeniu w drzewie od korzenia w dół do wskazania
na puste poddrzewo, przy czym wybór między lewym a prawym poddrzewem odbywa się z jednakowym prawdopodobieństwem 1/2, i zastąpienie go
wskazaniem na nowe poddrzewo złożone z jednego węzła (w tym przypadku prawdopodobieństwo wyboru pola zawierającego null nie jest jednakowe i
zależy od głębokości węzła).
1
• generuje się losową permutację liczb od 1 do n a następnie tworzy się drzewo
binarne o strukturze odpowiadającej binarnemu drzewu poszukiwania uzyskanemu przez wstawianie do niego kolejnych liczb losowej permutacji (w przykładowym drzewie struktura odpowiada drzewu przeszukiwania dla permutacji
h2, 1, 4, 3i).
Zadanie
Napisz w języka Ada pakiet dostarczający typy, procedury i funkcje umożliwiające, między innymi, tworzenie losowych drzew binarnych oraz liczenie ich wysokości.
Wykorzystaj stworzony pakiet do eksperymentalnego badania jak wysokość losowo zbudowanego drzewa zależy od liczby jego elementów przy różnych sposobach
konstrukcji.
Przeprowadź odpowiednie eksperymenty i przygotuj wykres zależności oczekiwanej wysokości losowo zbudowanego drzewa binarnego w zależności od liczby jego
węzłów (od 10 do 1000 co 10) i sposobu jego generowania.
Zaprezentuj swój program (dostarcz dokumentację w HTML wygenerowaną programem GPS) i przedstaw wyniki eksperymentów.
2