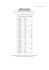Metoda simpleks

Wprowadzone oznaczenia:
 y00 
c B −1b  y10 
y0 ≡  B −1  ≡  
 B b   M 
 
 ym 0 
gdzie
a j , j ∈ RN
 y0 j 
c B −1a − c j   y1 j 
y j ≡  B −1 j
≡ 
 B a j
  M 
 ymj 
oraz
oznaczają kolumny macierzy N.
Funkcja celu x0
∑y
x0 = y00 −
Poszukiwanie rozwiązań bazowych
dopuszczalnych
xj
0j
j∈RN
m funkcji ograniczeń
x Bi = yi 0 −
∑y
ij
x j , dla i = 1,..., m
j∈R N
Wydział
Wydział Elektroniki studia I st.
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Postać początkowej tablicy simpleksowej
Postać początkowej tablicy simpleksowej dla omawianego
przykładu
− xN
x0
xB
cB B −1b cB B −1 N − c N
−1
−1
B b
B N
cB = 0
Kierunek Elektronika III r.
x0
xB
− xN
0 − cN
b N
dla przypadku gdy cB=0 tzn. pierwsze rozwiązanie bazowe dopuszczalne odpowiada za
punkt wierzchołkowy x
x = [0,...,0]T .
Wydział
Wydział Elektroniki studia I st.
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Kierunek Elektronika III r.
x1 + x2 ≤ 5




X =  x : − x1 + x2 ≤ 0 , x ≥ 0
 6 x + 2 x ≤ 21

1
2


max x0 = 2x1 + 1x 2
x∈ X
max x0 = 2x1 + 1x2 + 0 x3 + 0 x4 + 0 x5
x∈ X
x1 +
x 2 + x3 +


X =  x : − x1 + x 2 + 0 +

 6 x1 + 2 x 2 + 0 +
0+
x4 +
0+
0= 5

0= 0
x5 = 21
 x3 
x3
x 
xB = x4
4

x
 
x5
x =  B  =  x5  ≥ 0
 xN   x 
 1
x 
xN =  1 
 x2 
x2 
xN
xB
x1
x2
-2
-1
x0
0
x3
5
1
1
x4
0
-1
1
x5
21
6
2
Wydział
Wydział Elektroniki studia I st.
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Kierunek Elektronika III r.
Polepszanie bazowego rozwiązania dopuszczalnego
Polepszanie rozwiązania bazowego dopuszczalnego
θ rk = min ( yi 0 / yik , yik > 0).
i =1,...,m
x0 = y 00 −
∑
y0 j x j
Gdy mamy nie-zdegenerowane rozwiązanie bazowe dopuszczalne takie, Ŝe
j∈R N
y0 j < 0 dla pewnego j = k , k ∈ RN oraz yik > 0
dla przynajmniej jednego i wówczas moŜna z niego otrzymać lepsze bazowe
rozwiązanie dopuszczalne przez wymianę jednej z kolumn macierzy B na kolumnę
macierzy N.
zawsze x j ≥ 0,
zatem gdy xk ↑ to równieŜ x0 ↑ gdy y0 k ≤ 0
x Bi = yi 0 −
∑y
ij
xk =
x j , dla i = 1,..., m
j∈R N
Element centralny yrk leŜy na przecięciu wybranego wiersza xbr i
wybranej kolumny xk.
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Wydział
Wydział Elektroniki studia I st.
Kierunek Elektronika III r.
yr 0
−
y rk
y rj
∑{ } y
j ∈R N − k

y y 
x Bi =  yi 0 − ik r 0  −
y rk 

xj −
rk

∑{ } y
j∈R N − k
ij
−
1
x Br
y rk
yik y rj 
y
 x j + ik x Br
y rk 
y rk
Element centralny yrk leŜy na przecięciu wybranego wiersza xBr i wybranej kolumny xk.
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Wydział
Wydział Elektroniki studia I st.
Kierunek Elektronika III r.
Optymalne rozwiązanie zadania programowania liniowego PL metodą
simpleks
Pierwsza tablica simpleks-I rozwiązanie bazowe dopuszczalne
Kryterium
y0 j ≥ 0 dla ∀j ∈ RN
optymalności
......
x
y
0
00...
x
y
x0 0 y0000 ...
......
xBi xBiy yiO iO y...
iO...
xBi
j
−...−x xj −j x......
...
y
0
j
y
...
y0 j0 j ...
...
......
...y y y...
ij ...
−...−xkxk− x...k...
...
k...
y0yk0 k y0...
...
......
...y y yik......
......
dla i ∈ {1,..., m}
r 0...
xBr xBryry0r 0 y...
xBr
......
x x x Bm
y y ym...0...
...
......
...y y y...
rj ...
rj rj
...
......
...
y y ymj......
...
Twierdzenie 4.5
Rozwiązanie bazowe dopuszczalne układu równań Ax=b
Kryterium
jest rozwiązaniem optymalnym zadania PL, jeśli są spełnione dwa warunki:
dopuszczalności
yio ≥ 0
(i) Warunek prymalnej dopuszczalności:
yi 0 ≥ 0 dla i ∈ {1,..., m}
(ii) Warunek optymalności
y 0 j ≥ 0 dla ∀j ∈ RN
Bm
Bm
Wydział
Wydział Elektroniki studia I st.
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Kierunek Elektronika III r.
xk
yr 0 / yrk
yrj / yrk
...
...
...... ...
...y y yrk...... ...
rkrk
...
...... ...
...
ymk ymk
ymk
...... ...
mjmj
Wydział
Wydział Elektroniki studia I st.
Kierunek Elektronika III r.
Algorytm simpleks dla ograniczeń mniejszościowych
Krok 1. (start). Rozpoczynamy algorytm od znalezienia pierwszego rozwiązania
− xj
...
... − xBr ...
x0 y00 − ( y0k yr 0 / yrk ) ... y0 j − ( y0k yrj / yrk ) ... − y0k / yrk
...
...
...
xBi yi0 − ( yik yr 0 / yrk ) ... yij − ( yik yrj / yrk )
− yik / yrk
...
... 1 / yrk
...
ik ik
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Polepszona tablica simpleks odpowiada za następne rozwiązanie bazowe
dopuszczalne o większej wartości funkcji celu.
...
...
m 0m 0
ij ij
...
bazowego dopuszczalnego. NaleŜy sprawdzić dopuszczalność
rozwiązania: czy yi 0 ≥ 0 dla i = 1,..., m Tak - idź do kroku 2, Nie – STOP.
y0 j ≥ 0 dla kaŜdego
Krok 2. (test optymalności). Czy
j ∈ RN ?
• Tak - to aktualne rozwiązanie jest optymalne.
• Nie -
...
...
idź do kroku 3.
Krok 3. (Wybór zmiennej wchodzącej do bazy). Wybierz jako zmienną wchodzącą
bazy taką zmienną x k , k ∈ R N dla której
Typową regułą jest wybór zmiennej
y0k =
xk
y0 k < 0.
do
jest reguła dla której:
min {y
0j
}
, y0 j ≤ 0
j ∈R N
IdŜ do kroku 4.
Wydział
Wydział Elektroniki studia I st.
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Kierunek Elektronika III r.
Wydział
Wydział Elektroniki studia I st.
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Kierunek Elektronika III r.
Algorytm simpleks (prymalny) c.d.
Schemat reguły przeliczenia współczynników w tablicy simpleks
wg metody eliminacji Gauss’a
Krok 4. (wybór zmiennej usuwanej z bazy). Wybierz jako zmienną usuwaną z bazy
taką zmienną
x , dla której
Br
θ rk = min ( yi 0 / yik , yik > 0).
i =1,...,m
Jeśli wiele zmiennych spełnia ten warunek, wybierz arbitralnie jedną z nich.
p - element centralny (główny)
q – dowolny element w wierszu centralnym (głównym)
r – dowolny element w kolumnie centralnej (głównej)
s – dowolny pozostały element
IdŜ do kroku 5.
Krok 5. (eliminacja Gauss’a). Wyznacz
x j , j ∈ RN − {k }
Podstaw
oraz zmiennej
xk
 1
p q   p
r s  ⇒  − r

 
 p
oraz x Bi , i ≠ R N , względem zmiennych
xBr zgodnie z wyprowadzonym wzorem.
x j = 0, j ∈ R N − {k } i x Br = 0 , wyznacz pozostałe elementy tablicy
xij
q 
p 

rq
s− 
p 
aby otrzymać nowe rozwiązanie bazowe dopuszczalne.
Idź do kroku 2.
Krok ten czasami nazywa się wymianą zmiennej bazowej ( piwotyzacją).
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Wydział
Wydział Elektroniki studia I st.
Kierunek Elektronika III r.
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Wydział
Wydział Elektroniki studia I st.
Kierunek Elektronika III r.
Przykład zadania programowania liniowego – metoda prymalna simpleks
- I rozw. bazowe dopuszczalne.
Krok 1. (start). Rozpoczynamy algorytm od znalezienia pierwszego rozwiązania bazowego
dopuszczalnego. NaleŜy sprawdzić dopuszczalność rozwiązania.
Przykład zadania programowania liniowego – metoda prymalna simpleks cd.
- II rozw. bazowe dopuszczalne.
Krok 5. (eliminacja Gauss’a). Wyznacz
idź do Kroku 3 – wybrano x2, Krok 4 –
wybrano x3, Krok 5 - metoda eliminacji Gauss’a.
Krok 2. (test optymalności).
y 0 j ≥ 0 dla ∀j ∈ RN
Nie spełniony test optymalności - idź do Kroku 3.
x5
x2
x0
7
1/3
-1/3
x3
3/2
-1/6
2/3
∧
x4
7/2
1/6
4/3
x0 = 0
x1
7/2
1/6
1/3
Krok 4. (wybór zmiennej usuwanej z bazy) - - zmienna x5 . IdŜ do kroku 5.
Rozwiązanie bazowe dopuszczalne:
x0
0
nowa tablicę simpleksów. Idź do kroku 2.
Krok 2. (test optymalności). Nie spełniony -
Tak - idź do kroku 2,
X1
x2
Wartość funkcji celu:
-2
-1
x = [ x3 , x4 , x5 , x1.x2 ]T = [5, 0, 21, 0, 0]T
x3
5
1
1
x4
0
-1
1
x5
21
6
2
∧
3 7 7
x = [ x3 , x4 , x1 , x5 .x2 ]T = [ , , , 0, 0]T
2 2 2
x0 = 7
Rozwiązanie bazowe dopuszczalne:
Zmienna x3: 5/1
Zmienna x4: nie
Zmienna x5: 21/6
min dla x5
Element centralny yrk – w
kolorze zielonym
Wartość funkcji celu:
Element centralny yrk – w kolorze zielonym
Wydział
Wydział Elektroniki studia I st.
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Kierunek Elektronika III r.
Przykład zadania programowania liniowego – metoda prymalna simpleks cd.
- III rozw. bazowe dopuszczalne = rozwiązanie optymalne.
Wydział
Wydział Elektroniki studia I st.
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Kierunek Elektronika III r.
Zadanie programowania liniowego PL dla ograniczeń mniejszościowych
ZałoŜenia:
1. Zbiór X rozwiązań dopuszczalnych
Krok 2. (test optymalności).
Tak - to aktualne rozwiązanie jest optymalne.
X ≠0
2. algorytm simpleks startuje z bazowego dopuszczalnego rozwiązania oraz w
trakcie jego realizacji nie występuje degeneracja
I. Zadanie programowania liniowego PL posiada jedno rozwiązanie
x5
x3
x0
31/4
1/4
1/2
x2
9/4
-1/4
3/2
x4
1/2
1/2
-2
x1
Rozwiązanie bazowe optymalne:
Wartość optymalna funkcji celu:
11/4
∧
1/4
x0
II. Zadanie programowania liniowego – zadanie PL nieograniczone
Twierdzenie 4.2
Jeśli zadanie PL jest nieograniczone, to istnieją rozwiązania
bazowe dopuszczalne xB oraz wektor y K taki, Ŝe:
y0 k < 0 i yik ≤ 0 dla i = 1,..., m
Wówczas zbiór rozwiązań jest pusty.
x1 , x2 ≥ 0
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
x1
x2
-2
2
-1
1
9
-1
3
x0
7
x5
x2
x5
x3
1/3
-1/3
x0
31/4
1/4
1/2
9/4
-1/4
3/2
5
1
1
x3
3/2
-1/6
2/3
x4
0
-1
1
x4
7/2
1/6
4/3
x4
1/2
1/2
-2
x5
21
6
2
x1
7/2
1/6
1/3
x1
11/4
1/4
-1/2
Wartość optymalna funkcji celu:
Przypadki szczególne cd.
-1
x2
-1
Rozwiązanie bazowe optymalne:
Kierunek Elektronika III r.
0
x1
-2
∧
Wydział
Wydział Elektroniki studia I st.
− x1 + x2 ≤ 2
− x1 + 3x2 ≤ 9
0
x2
x3
-1/2
9 1 11
x = [ x2 , x4 , x1 , x5 .x3 ] = [ , , , 0, 0]T
4 2 4
∧
31
x0 =
4
T
min x0 = − x1 − 2 x2 ,
x∈ X
Przykład:
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
Przykład:
x1 + x2 ≤ 5




X =  x : − x1 + x2 ≤ 0 , x ≥ 0
 6 x + 2 x ≤ 21

1
2


max x0 = 2x1 + 1x2
y 0 j ≥ 0 dla ∀j ∈ RN
Wydział
Wydział Elektroniki studia I st.
Kierunek Elektronika III r.
Technika optymalizacji
Dr inŜ. Ewa Szlachcic
11 9
1
x = [ x1 , x2 , x3 , x4 .x5 ]T = [ , , 0, , 0]T
4 4
4
31
x0 =
4
Wydział
Wydział Elektroniki studia I st.
Kierunek Elektronika III r.