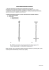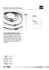Linia dwuprzewodowa [ ] [ ] [ ]

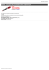
Linia dwuprzewodowa
Obliczanie pojemności linii dwuprzewodowej
1. Wstęp
Pojemność kondensatora można obliczyć w prosty sposób znając wartości
zgromadzonego na nim ładunku i napięcia między okładkami:
C=
Q
.
U
(1)
Skorzystamy z tej zależności, aby obliczyć pojemność linii dwuprzewodowej. Okładkami
kondensatora będą w takim przypadku przewody, o których założymy że są nieskończenie
długie, mają przekrój kołowy i są równoległe do siebie (Rys. 1a).
(b)
(a)
Rys. 1 Linia dwuprzewodowa (a) oraz kabel z powłoką przewodzącą (b)
Ponieważ pojemność zależy tylko od geometrii linii, możemy umieścić na niej
dowolny ładunek, obliczyć wytwarzany przez niego na każdym przewodzie potencjał,
a następnie napięcie – jako różnicę potencjałów (V1 – V2) między przewodami. Jako że
rozpatrujemy linię nieskończenie długą, to będziemy się posługiwać nie ładunkiem, lecz
gęstością liniową ładunku τ (C/m), a obliczymy wartość względną pojemności Cl
– przypadającą na jednostkę długości linii:
C
τ 
 F  C [ F]
m .
Cl   =
=
 m  l [ m ] V1 − V2 [ V ]
(2)
2. Pole cienkich osi obdarzonych ładunkiem
W celu wyznaczenia pojemności układu dwóch nieskończenie długich walców
rozpatrzymy najpierw pole elektrostatyczne dwóch nieskończonych osi (o zerowym
przekroju), na których ładunek rozłożony jest ze stałą gęstością liniową τ i -τ (Rys. 2).
Wykażemy, że pole elektryczne takich obdarzonych ładunkiem nieskończenie cienkich
osi jest równoważne polu wytworzonemu przez przewody o niezerowych przekrojach.
Rys. 2 Nieskończone osie z równomiernie rozłożonym ładunkiem
Potencjał elektryczny w punkcie P obliczamy jako superpozycję potencjałów
pochodzących od obu osi i możemy wyrazić go wzorem:
V ( P) = −
r
τ
τ
τ
τ
ln r1 +
ln r2 =
ln 2 =
ln a ,
2πε
2πε
2πε r1 2πε
(3)
gdzie r1 i r2 są odległościami punktu P od osi:
r1 =
y2 + ( x − b) ,
2
r2 =
y2 + ( x + b) .
2
(4)
Linie ekwipotencjalne tworzą punkty, w których V(P) = const. Z równania (3) możemy
wyznaczyć zależność, jaką linie te są opisywane :
r2
= a = const
r1
(5)
i jak łatwo wykazać są one okręgami o równaniu:
y2 + ( x − h) = R2 ,
2
(6)
gdzie:
h=
2
a2 + 1
b,
a2 −1
R=
2ab
a2 −1
.
(7)
3. Pole linii dwuprzewodowej
W elektrostatyce powierzchnia przewodnika jest powierzchnią ekwipotencjalną. Dla
układu złożonego z dwóch przewodów o przekroju kołowym potencjał na powierzchni
każdego przewodu również będzie stały. Na powierzchniach przewodów i w ich otoczeniu
(na zewnątrz przewodów) potencjał można opisać równaniem (3), czyli takim samym jak
dla linii z nieskończenie cienkich, naładowanych osi. Możemy więc tak dobrać położenia
osi (parametr b), aby ich pole było równoważne polu przewodów o przekroju kołowym.
Linie ekwipotencjalne wyznaczone dla nieskończenie cienkich, naładowanych osi –
okręgi pokazane na Rys. 2 – są więc równoważne powierzchniom przewodów
o niezerowym przekroju poprzecznym.
Pomiędzy wielkością b charakteryzującą położenie osi elektrycznej a wielkością h
charakteryzującą położenie osi geometrycznej powierzchni ekwipotencjalnej zachodzi
związek:
b2 = h2 − R 2 .
(8)
Parametr a, przy którym linie ekwipotencjalne wyznaczają powierzchnie przewodników
wyraża się wzorem:
a=
h+b
h+b
R
,
=
=
h−b
h−b
R
(9)
w którym h i R oznaczają położenie na osi X i promień przewodu. Podstawiając h = h1
i R = R1 oraz h = h2 i R = R2 otrzymamy dwie wartości a – dla dwóch przewodów: a1 > 1,
gdy r2 > r1 (prawa strona na Rys. 2 – dla dodatnich x) oraz a2 < 1, gdy r2 < r1 (lewa strona
na Rys. 2 – dla ujemnych x). Wielkości h1, h2 i b wyznacza się z zależności:
b 2 = h12 − R12 = h22 − R22 ,
h1 − h2 = D
(10)
( R1 ≥ R2 ) ,
(11)
gdzie D jest odległością między osiami walców.
Po przekształceniach otrzymujemy:
h1 =
D 2 + R12 − R22
R 2 − R22 − D 2
, h2 = 1
.
2D
2D
(12)
Pojemność na jednostkę długości układu dwóch walców:
Cl =
τ
2πε
2πε
=
=
V1 − V2
a
 R h −b
ln 1
ln  1 ⋅ 2
 R h −b
a2
 2 1



=
2πε
 R h +b
ln  2 ⋅ 1
 R h +b
 1 2



.
(13)
3
4. Pole kabla niewspółosiowego
Te same zależności można zastosować gdy chcemy obliczyć pojemność
jednożyłowego kabla z przewodzącą powłoką (Rys. 1b). Podstawiając we wzorach (12)
i (13) wartość D spełniającą warunek:
0 ≤ D < R1 – R2
(14)
otrzymamy położenia osi geometrycznych przewodów h1 i h2 o tym samym znaku (leżące
na tej samej połowie osi X) oraz wartość pojemności dla kabla.
5. Przypadki szczególne
Możemy teraz rozpatrywać przypadki szczególne, w których wzór (13) zapiszemy
w uproszczonych postaciach.
Linia dwuprzewodowa, o takich samych przewodach:
R1 = R2 ⇒
h1 =
D
D
, h2 = −
2
2
Cl =
πε
2
 D

 D 

ln
+ 
−1 

 2R

 2R 


;
(15)
Kabel koncentryczny (idealnie symetryczny):
D =0⇒
h1 , h2 → ∞
Cl =
2πε
;
R1
ln
R2
(16)
Linia dwuprzewodowa, o przewodach dużo cieńszych niż odległość między przewodami:
R1 , R2 << D ⇒
b≈
D
2
Cl ≈
πε
D
ln
R1 R2
.
(17)
Ostatni wzór można wyprowadzić zakładając, że oś elektryczna pokrywa się z osią
geometryczną przewodu. Wówczas:
V1 ≈ −
τ
τ
τ
D
ln R1 +
ln D =
ln ,
2πε
2πε
2πε R1
(18)
V2 ≈ −
R
τ
τ
τ
ln D +
ln R2 =
ln 2 ,
2πε
2πε
2πε D
(19)
τ
D2
τ
D
ln
=
ln
.
2πε R1 R2 πε
R1 R2
(20)
V1 − V2 ≈
4
6. Linia dwuprzewodowa nad ziemią
Pojemność linii dwuprzewodowej zawieszonej nad ziemią można obliczyć stosując
metodę odbić zwierciadlanych. Zakładamy, że przewody mają takie same promienie R,
wielokrotnie mniejsze od odległości między przewodami D (Rys. 3).
Rys. 3 Linia dwuprzewodowa zawieszona nad ziemią
Obliczając potencjał dla każdego z przewodów musimy jeszcze uwzględnić przewody
„zwierciadlane”:
h1 = h,
h2 = h + D sin α ,
(21)
V1 =
2h D
τ
τ
( − ln R + ln 2h1 + ln D − ln r ) = ln 1 ,
2πε
2πε
rR
(22)
V2 =
τ
τ
rR
.
( ln R − ln D − ln 2h2 + ln r ) = ln
2πε
2 πε 2h2 D
(23)
Po przekształceniach otrzymujemy wartość pojemności linii na jednostkę długości:
Cl =
πε

D

1 + sin α
D

h
ln  ⋅
2
R
D D

1
+
 2h  + h sin α

 








.
(24)
5
Literatura
1. Ryszard Sikora, Teoria Pola Elektromagnetycznego, Wydawnictwa NaukowoTechniczne, 1997, wydanie trzecie zmienione, str. 83–119
2. Maciej Krakowski, Elektrotechnika Teoretyczna t.2, Wydawnictwa Naukowe PWN,
1999, wydanie szóste, str. 52–55, 58–59, 65–69
3. David J. Griffiths, Podstawy Elektrodynamiki, Wydawnictwa Naukowe PWN, 2001
wydanie pierwsze, str. 120–133, 146–152
4. Markus Zahn, Pole Elektromagnetyczne, Państwowe Wydawnictwo Naukowe, 1989,
str. 68–77, 104–113
Równania (13), (16) i (24) jako funkcje w języku MATLAB
równanie (13)
function [C,a1,a2,h1,h2,b] = r13(D,R1,R2,epsilon)
h1
h2
b
a1
a2
=
=
=
=
=
(D.^2+R1.^2-R2.^2)./2./D;
(-D.^2+R1.^2-R2.^2)./2./D;
sqrt(h1.^2 - R1.^2);
abs(b+h1)./R1;
abs(b+h2)./R2;
C = abs(2*pi*epsilon/log(a1/a2));
równanie (16)
function C = r16(D,R1,R2,epsilon)
C = abs(2*pi*epsilon./log(R1./R2));
równanie (24)
function C = r24(D,R,h,alfa,epsilon)
C = abs(...
pi*epsilon...
./(log(D./R)...
.*sqrt((1+D./h.*sin(alfa))...
./(1+(D./2./h).^2+(D./h).*sin(alfa)))));
6
Zadania
Używając funkcji em1_linia2p należy rozwiązać przedstawione poniżej zadania.
Na podstawie wprowadzonych danych wejściowych funkcja rozpoznaje, który przypadek
jest rozpatrywany i oblicza pojemność linii na jednostkę długości. Rozwiązując zadanie 1
i 2 należy podać przy wywołaniu funkcji: odległość D między osiami przewodów (lub
między osiami żyły i powłoki) oraz promienie R1 i R2 przewodów (lub odpowiednio
promień żyły i promień powłoki):
C = em1_linia2p(D,R1,R2);
Rozwiązując zadanie 3 należy wprowadzić: odległość D między osiami przewodów,
promień R (jednakowy dla obu przewodów), wysokość h zawieszenia linii nad ziemią
oraz kąt α opisujący rozmieszczenie przewodów (wyrażony w radianach):
C = em1_linia2p(D,R,h,alfa);
Wprowadzenie
nieprawidłowych danych
powoduje
wyświetlenie
komunikatu
o błędzie. Pojawia się on, gdy z podanych wartości (D, R1 i R2) lub (D, R, h, i α) nie
można stworzyć prawidłowej geometrii linii. Podanie prawidłowych wartości powoduje
wyświetlenie rysunku przedstawiającego geometrię linii oraz wyniki. Jako dane należy
wprowadzać tylko liczby, które są rozumiane jako wartości odpowiednich parametrów
wyrażone w jednostkach SI. Dane należy wprowadzać w takiej kolejności, w jakiej
przedstawiono je powyżej.
1) Linia dwuprzewodowa
a) Dla danych wartości R1, R2, i D obliczyć dokładną (z funkcji em1_linia2p)
i przybliżoną (z wzoru 17) wartość pojemności układu.
Dane:
D = 20 mm
R1 = 1,5 mm
R2 = 3,5 mm
b) Obliczyć pojemności (dokładną i przybliżoną) dla kilku innych (większych)
wartości D.
c) Obliczyć pojemności (dokładną i przybliżoną) dla kilku innych wartości R1.
Dla wyników uzyskanych w punktach a, b i c wyznaczyć błąd jaki popełniamy
korzystając ze wzoru przybliżonego (17) zamiast dokładnego (13) – wyznaczyć błąd
względny obliczania pojemności i wyrazić go w procentach.
7
2) Kabel niewspółosiowy
a) Dla danych wartości R1, R2, i D obliczyć dokładną (z funkcji em1_linia2p)
i przybliżoną (z wzoru 16) wartość pojemności układu.
Dane:
D = 0,2 mm
R1 = 2 mm
R2 = 30 mm
b) Obliczyć pojemności (dokładną i przybliżoną) dla kilku innych (większych)
wartości D.
c) Obliczyć pojemności (dokładną i przybliżoną) dla kilku innych wartości R1.
Dla wyników uzyskanych w punktach a, b i c wyznaczyć błąd obliczania pojemności
jaki popełniamy korzystając ze wzoru przybliżonego (16) zamiast dokładnego (13).
Określić kiedy możemy korzystać ze wzoru przybliżonego. Dla jakiego przypadku
stosując ten wzór otrzymujemy dokładne wyniki?
3) Linia dwuprzewodowa zawieszona nad ziemią
a) Dla danych wartości R, D, h i α obliczyć pojemność linii (korzystając z funkcji
em1_linia2p).
Dane:
D = 15 mm
R = 2 mm
h = 2,5 mm
α = π/6
b) Zbadać jaki wpływ na pojemność wywiera wysokość h zawieszenia linii nad
ziemią oraz rozmieszczenie przewodów (α).
c) Jaki błąd jest popełniany, jeżeli nie uwzględnia się wpływu ziemi na pojemność
linii dwuprzewodowej?
W sprawozdaniu z ćwiczenia należy umieścić
przeprowadzonych obliczeń (pojemności dokładnej i
wyniki wszystkich
przybliżonej, błędu
popełnianego przy korzystaniu z wzoru przybliżonego zamiast dokładnego) zebrane
w tabelach i przedstawione na wykresach. Sprawozdanie musi również zawierać
wnioski (na podstawie wyników).
(ks) 2009-03-10, popr. 2014-10-01
8