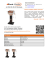Pole powierzchni całkowitej stożka jest równe 81 π cm2

Zadanie: Pole powierzchni całkowitej stożka jest równe 81 π cm2 , a jego objętość wynosi
81 π cm3 . Oblicz miarę kata rozwarcia stożka. Wynik podaj z dokładnością do 1◦ .
Oznaczenia (patrz rysunek)
Szukane:
H - wysokość stożka
r - promień podstawy stożka
L - długość tworzącej
S - pole powierzchni bocznej
V - objętość stożka
S = 81 cm2
V = 81 cm3
Kąt α będący kątem wierzchołkowym w równoramiennym trójkącie tworzonym przez przecięcie stożka płaszczyzną prostopadłą do podstawy i przechodzącą
przez wierzchołek. Kąt β jest połową kąta α
Objętość stożka:
1
V = πr2 H = 81π
3
(1)
S = πrL + πr2 = 81π
(2)
Pole powierzchni całkowitej:
Dodatkowo z twierdzenia Pitagorasa wiem, że
L2 = r 2 + H 2
(3)
Nie rozwiązuję tego układu równań ogólnie (choć jest to wykonalne, ale skomplikowane), tylko
używam danych z zadania: S = 81π, V = 81π. Zaznaczam, że fizyczne wymiary w równaniach
mogą się pozornie nie zgadzać, ponieważ pominąłem centymetry sześcienne i kwadratowe.
Dążę do znalezienia r oraz H. Wtedy
r
(4)
H
W równaniu (2) dzielę obie strony przez π, następnie przez r, następnie odejmuję r od obu
stron. Dostaję:
81
−r =L
(5)
r
Podnoszę obie strony równania (5) do kwadratu i podstawiam kwadrat L z równania (3)
tg β =
81
812
−2
r + r2 = r2 + H 2
2
r
r
Upraszczam kwadrat r oraz r w środkowym ułamku Obliczam kwadrat r.
812
− 162 = H 2
r2
zatem
r2 =
812
H 2 + 162
(6)
(7)
Wstawiam kwadrat r do równania (1), upraszczam w nim π i mnożę przez 3.
812
H = 3 · 81
H 2 + 162
(8)
Dzielę obie strony przez 3*81, mnożę przez mianownik. Dostaję równanie kwadratowe na H.
27H = H 2 + 162
zatem
H 2 − 27H + 162 = 0
Rozwiązuję równanie (9) Wyróżnik ∆ = 272 − 4 · 162 = 81 = 92 . Wobec tego:
H1 = (27 − 9)/2 = 9 oraz H2 = (27 + 9)/2 = 18.
(9)
Wartości H podstawiam do równania (7) i obliczam kwadrat r. Otrzymuję dwa rozwiązania:
812
812
27
2
=
27
oraz
r
=
=
(10)
2
2
2
9 + 162
18 + 162
2
q
√
Wynika z tego, że r jest równe 3 3 lub 3 3/2. Podstawiam pary (H, r) do równania (4) (patrz
poprzednia strona).
r12 =
q
√
3 3
1
tg β1 =
=√
9
3
oraz
tg β2 =
3 3/2
9
s
=3
3
2
(11)
Pierwsze rozwiązanie odpowiada kątowi β1 = 30◦ , drugie kątowi około β2 ≈ 74.8◦
Szukany kąt rozwarcia stożka α jest podwojonym katem β. Zadanie ma więc dwa rozwiązania:
α1 = 60◦ lub α2 ≈ 150◦
Sprawdzę jeszcze, czy dostaję właściwe pole powierzchni i objętość.
q
√
√
√
Dla H = 9, r = 3 3 dostaję L = 92 + (3 3)2 = 6 3
√
√
√
S = π · 3 3 · 6 3 + π · (3 3)2 = 81π
√
1
V = π · 9 · (3 3)2 = 81π
3
r
q
Dla H = 18, r = 3 3/2 dostaję L =
q
q
q
92 + (3 3/2)2 = 15 3/2
q
q
S = π · 3 3/2 · 15 3/2 + π · (3 3/2)2 = 81π
q
1
V = π · 18 · (3 3/2)2 = 81π
3