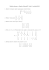3. Elementy odwrotne

ARYTMETYKA MODULARNA
Grzegorz Szkibiel
Wiosna 2014/15
Spis tre±ci
1 Denicja kongruencji i jej podstawowe wªasno±ci
3
2 Systemy pozycyjne
8
3 Elementy odwrotne
12
4 Pewne zastosowania elementów odwrotnych
17
5 Maªe Twierdzenie Fermata
19
6 Twierdzenie Eulera
22
7 Twierdzenie Lagrange'a
26
8 Chi«skie Twierdzenie o Resztach
29
9 RSA i gra w orªa i reszk¦ przez telefon
34
10 Kongruencje wy»szych stopni
38
11 Liczby pseudopierwsze
44
12 Pierwiastki pierwotne
49
13 Istnienie pierwiastków pierwotnych
53
14 Logarytm dyskretny
58
15 Pewne zastosowania pierwiastków pierwotnych
61
2
Wykªad 3
Elementy odwrotne
Jak do tej pory, zauwa»yli±my, »e kongruencje mo»na dodawa¢, odejmowa¢ i
mno»y¢ stronami. Zauwa»yli±my te», »e, ogólnie, nie mo»na dzieli¢ kongruencji stronami. Co wi¦cej, nie zachodzi te» prawo skracania: 4 ≡ 12 (mod 8),
ale 1 ̸≡ 3 (mod 8).
3.1 Twierdzenie.
Przypu±¢my, »e
bc (mod m) dla pewnych liczb a, b
m
encja a ≡ b (mod NWD(m,
).
c)
c
jest dodatni¡ liczb¡ caªkowit¡ oraz
oraz
m > 0.
ac ≡
Wówczas zachodzi kongru-
Oznaczmy d = NWD(m, c) i zapiszmy c = dc′ , m = dm′ . Wówczas
′
′
′
NWD(c , m ) = 1. Z drugiej strony, m | c(a − b), czyli dm | dc (a − b), st¡d
m′ | c′ (a − b). Poniewa» NWD(c′ , m′ ) = 1, wi¦c m′ | a − b. Skoro jednak
m′ = md , wi¦c mamy tez¦.
Dowód.
′
Wracaj¡c do przykªadu poprzedzaj¡cego powy»sze twierdzenie, docelowa kongruencja, to 1 ≡ 3 (mod 2), poniewa» 8/NWD(4, 8) = 4. Zauwa»my
jeszcze dwa nast¦puj¡ce fakty.
1. Ka»d¡ kongruencj¦ mo»na skraca¢ przez liczb¦ wzgl¦dnie pierwsz¡ z moduªem, np. wiadomo, »e 48 ≡ 12 (mod 9), wówczas 12 ≡ 3 (mod 9).
2. Je±li moduª dzieli si¦ przez liczb¦, przez któr¡ chcemy skróci¢ kongruencj¦, to równie» skracamy moduª, np. wiadomo, »e 48 ≡ 12 (mod 9),
wówczas 16 ≡ 4 (mod 3).
Cz¦sto si¦ zdarza, »e trzeba ª¡czy¢ kongruencje o ró»nych moduªach. Je±li
a ≡ b (mod m) oraz a ≡ b (mod n), to nie musi koniecznie zachodzi¢ kongruencja a ≡ b (mod mn). Na przykªad, 2 ≡ 10 (mod 8), 2 ≡ 10 (mod 4),
ale 2 ̸≡ 10 (mod 32). Potrzebne jest tu dodatkowe zaªo»enie.
12
3.2 Twierdzenie.
a ≡ b (mod m)
Przypu±¢my, »e
oraz
NWD
(m, n) = 1.
a ≡ b (mod n)
Wówczas
⇔
a ≡ b (mod mn).
⇒. Poniewa» m | a − b, wi¦c istnieje taka liczba caªkowita k , »e
mk = a − b. Skoro n | mk oraz NWD(m, n) = 1, wi¦c n | k . Zatem istnieje
taka liczba k1 , »e nk1 = k . St¡d mnk1 = a − b, czyli a ≡ b (mod mn).
⇐. Skoro a ≡ b (mod mn), wi¦c a ≡ b (mod d) dla dowolnego dzielnika d
liczby mn. W szczególno±ci dla m oraz n.
Dowód
Powy»sze twierdzenie pozwala rozbija¢ kongruencje o du»ych zªo»onych
moduªach na kongruencje o ni»szych moduªach pierwszych. Jest to o tyle
istotne, »e ªatwiej jest wydedukowa¢ co± na temat podzielno±ci przez liczb¦
pierwsz¡ ni» przez liczb¦ zªo»on¡. Na przykªad, aby sprawdzi¢, czy 1729
przystaje do 1 modulo 12, wystarczy sprawdzi¢, czy zachodz¡ kongruencje
1729 ≡ 1 (mod 3) oraz 1729 ≡ 1 (mod 4). Jest to ªatwe, poniewa» cechy
podzielno±ci przez 3 i 4 s¡ ªatwe w zastosowaniu. Poniewa» liczba 1728 dzieli
si¦ zarówno przez 3 jak i przez 4, wi¦c wspomniane kongruencje zachodz¡.
Podobnie jak równania mo»na te» rozwi¡zywa¢ kongruencje. Generalnie,
je»eli dany jest moduª m oraz funkcja f okre±lona w zbiorze liczb caªkowitych i o warto±ciach caªkowitych, to pytamy jak znale¹¢ x, aby speªniona
byªa kongruencja f (x) ≡ 0 (mod m). W tym podrozdziale zajmiemy si¦
kongruencjami liniowymi, czyli takimi, dla których f (x) = ax + b, gdzie a
oraz b s¡ liczbami caªkowitymi. Aby upro±ci¢ zapis b¦dziemy dalej pisa¢
kongruencje liniowe w postaci
ax ≡ b (mod m)
(3.1)
Przypomnijmy, »e w zbiorze liczb rzeczywistych, aby rozwi¡za¢ równanie
ax = b, mno»ymy obie jego strony przez liczb¦ odwrotn¡ do a (o ile taka
istnieje, a nie istnieje tylko dla a = 0). Podobnie b¦dziemy post¦pujemy
w przypadku kongruencji liniowych. Dlatego zajmiemy si¦ teraz liczbami
odwracalnymi modulo m.
Liczb¦ a nazywamy odwracaln¡ modulo m je»eli istnieje taka liczba a′ , »e
aa′ ≡ 1 (mod m).
3.3 Przykªad. Poniewa» 2 · 6 ≡ 1
(3.2)
(mod 11), wi¦c liczby 6 oraz 2 s¡ odwra-
calne modulo 11. Zauwa»my, »e tak»e liczby ró»ni¡ce si¦ od 2 i 6 o wielokrotno±¢ 11 s¡ odwracalne modulo 11. Istotnie, mamy
2 · (6 + 11k) ≡ 2 · 6 ≡ 1
13
(mod 11).
Liczba 2 nie jest odwracalna modulo 8, poniewa» je±li 2a′ ≡ 1 (mod 8), to
oznacza to, »e 8 | 2a′ − 1, czyli 8 dzieli liczb¦ nieparzyst¡, co nie jest prawd¡.
Liczby odwracalne modulo m maj¡ bardzo wygodn¡ charakteryzacj¦ przedstawion¡ w twierdzeniu 3.5. Dowód tego twierdzenia dostarcza nam te» metody, jak szuka¢ elementu a′ . Potrzebny nam jednak b¦dzie lemat.
3.4 Lemat.
»e
Je±li
ax + by = d.
d=
NWD
(a, b),
to istniej¡ liczby caªkowite
Odwrotnie, dla dowolnych liczb caªkowitych
NWD
x oraz y ,
x oraz y ,
takie
(a, b) | ax + by.
Oznaczmy S = {am + bn : m, n ∈ Z}. Zauwa»my, »e w zbiorze S s¡
liczby dodatnie. Zatem, zgodnie z zasad¡ minimum, istnieje w S najmniejsza
liczba dodatnia. Oznaczmy j¡ przez q . Poka»emy, »e q jest dzielnikiem a.
Istotnie, zapiszmy a = eq + t, gdzie 0 ≤ t < q . Poniewa» q = am0 + bn0 dla
pewnych m0 , n0 , wi¦c t = (1 − em0 )a + (−n0 )b ∈ S . Zatem t = 0 gdy» w
przeciwnym wypadku mieliby±my sprzeczno±¢ z wyborem liczby q . Podobnie
pokazujemy, »e t | b.
Zauwa»ymy teraz, »e q jest najwi¦kszym wspólnym dzielnikiem liczb a i b.
W tym celu przypu±¢my, »e c > 0, c | a oraz c | b. Wówczas c | am + bn dla
dowolnych m i n, wi¦c w szczególno±ci, c | q . Zatem c ≤ q . W ostateczno±ci,
q = NWD(a, b) i q ∈ S co dowodzi pierwszej cz¦±ci twierdzenia.
Z drugiej strony, skoro NWD(a, b) jest dzielnikiem a oraz b, wi¦c jest te»
dzielnikiem dowolnego elementu zbioru S .
Dowód.
3.5 Twierdzenie. Liczba caªkowita a jest odwracalna modulo m wtedy i tylko
wtedy, gdy
NWD
(a, m) = 1.
⇒. Skoro istnieje taka liczba a′ , »e aa′ ≡ 1 (mod m), to istnieje te»
taka liczba caªkowita k , »e aa′ − 1 = km, albo aa′ − km = 1. Z poprzedniego
lematu wynika, »e NWD(a, m) = 1.
⇐. Je±li NWD(a, m) = 1, to istniej¡ liczby caªkowite x oraz y takie, »e
ax + my = 1, czyli m | ax − 1. Zatem a jest odwracalna modulo m.
Dowód
Aby obliczy¢ liczb¦ odwrotn¡ do a′ , nale»y znale¹¢ takie liczby x oraz y ,
»eby zachodziªa równo±¢ ax + my = 1. Liczby te znajdujemy stosuj¡c algorytm Euklidesa. Wówczas a′ = x. Dla przykªadu, znajd¹my 11′ modulo 31.
W tym celu wykonujemy nast¦puj¡ce obliczenia:
31 = 3 · 11 − 2
11 = 5 · 2 + 1
2 = 3 · 11 − 31
1 = 11 − 5 · 2.
14
Tak wi¦c 1 = 11 − 5 · 2 = 11 − 5 · (3 · 11 − 31) = 5 · 31 − 14 · 11. Zatem
11′ = −14 + 31 = 17.
Zauwa»my, »e je±li liczba caªkowita a jest odwracalna modulo m, to istnieje niesko«czenie wiele liczb a′ , które speªniaj¡ kongruencj¦ (3.2). Mówi¡c o
elementach odwracalnych, chcieliby±my tak»e zdeniowa¢ element odwrotny
do danego. Nale»y wi¦c wyró»ni¢ jeden z elementów a′ . Poka»emy, »e w zbiorze wszystkich elementów a′ speªniaj¡cych (3.2) zachodzi pewna regularno±¢.
3.6 Twierdzenie.
′
a
i
′′
a
ró»ni¡ si¦ o
aa′ ≡ 1 (mod m),
wielokrotno±¢ m.
Je±li
oraz
aa′′ ≡ 1 (mod m),
to liczby
Przypu±¢my, »e a′ − a′′ = qm + r dla q ∈ Z oraz 0 ≤ r ≤ m − 1.
Mamy aa′ − aa′′ = aqm + ar, albo aa′ − aa′′ ≡ ar (mod m). Zatem zachodzi
0 ≡ ar (mod m), czyli m | ar. Skoro jednak NWD(a, m) = 1, wi¦c m | r, a to
oznacza, »e r = 0.
Dowód.
Z powy»szego twierdzenia wynika, »e je±li liczba a jest odwracalna modulo m, to mo»emy mówi¢ o elemencie odwrotnym do a modulo m. Tak
wi¦c, je±li a ∈ Z jest odwracalny modulo m, to elementem odwrotnym do a
modulo m nazywamy liczb¦ b ∈ {0, 1, . . . , m − 1}, tak¡ »e ab ≡ 1 (mod m).
B¦dziemy przy tym pisa¢ b = a−1 mod m.
Zdeniujmy dodawanie +m oraz ·m modulo m w nast¦puj¡cy sposób:
a +m b = a + b mod m,
a ·m b = a · b mod m.
Z tak zdeniowanymi dziaªaniami dodawania i mno»enia, zbiór Zm speªnia
wszystkie aksjomaty ciaªa z wyj¡tkiem szóstego. Aksjomat szósty (istnienie
elementu odwrotnego do ka»dego niezerowego elementu ciaªa) jest speªniony
tylko dla liczb pierwszych m, co wynika z twierdzenia 3.5. Zatem zbiór Zp z
dziaªaniami +m i ·m jest ciaªem.
Wró¢my teraz do kongruencji (3.1). Ma ona rozwi¡zanie, je±li liczba a
jest odwracalna modulo m. Aby znale¹¢ to rozwi¡zanie, nale»y pomno»y¢
obie strony kongruencji (3.1) przez liczb¦ odwrotn¡ do a.
3.7 Przykªad. Rozwi¡»emy
3x ≡ 5 (mod 13). Wykorzystuj¡c algorytm
Euklidesa, otrzymujemy 3 · 9 − 13 · 2 = 1. Zatem 9 jest liczb¡ odwrotn¡ do 3
modulo 13. Mno»¡c obie strony naszej kongruencji przez 9 otrzymujemy
x ≡ 9 · 5 ≡ 6 (mod 13). Zatem 6 (i ka»da liczba, która si¦ ró»ni od 6
o wielokrotno±¢ 13) jest rozwi¡zaniem naszej kongruencji.
15
Je±li nie b¦dzie powiedziane inaczej, to od tej chwili b¦dziemy rozwa»a¢
tylko te rozwi¡zania kongruencji (3.1), które nale»¡ do Zm = {0, 1, . . . , m − 1}.
Je±li w tym zbiorze jest tylko jedno rozwi¡zanie, to mówimy, »e jest ono jednoznaczne lub jednoznaczne modulo m.
Je»eli a nie jest odwracalna modulo m, to rozwi¡zanie te» mo»e istnie¢.
Przedstawimy teraz twierdzenie, które mówi o istnieniu i jednoznaczno±ci
rozwi¡za«.
3.8 Twierdzenie.
za« je±li
d|b
Kongruencja (3.1) ma dokªadnie
oraz nie ma rozwi¡zania je±li
rozwi¡zaniem, to
d ró»nych
i ∈ {0, 1, . . . , d − 1}.
d - b.
d=
(a, m) rozwi¡d | b oraz x0 jest
x0 + md i mod m dla
NWD
Je»eli
rozwi¡za« wyra»a si¦ wzorem
Je±li d = 1, to jak ju» zauwa»yli±my, kongruencja (3.1) ma rozwi¡zanie. Aby pokaza¢ jego jednoznaczno±¢, przypu±¢my, »e x1 oraz x2 s¡ dwoma
rozwi¡zaniami (3.1). Zatem ax1 ≡ ax2 (mod m). Z twierdzenia 3.2 wynika
kongruencja x1 ≡ x2 (mod m), czyli x1 = x2 .
Zaªó»my teraz, »e d ̸= 1. Je±li d - b, to poniewa» d | a, wi¦c d - ax − b
dla »adnego x ∈ Z, a co za tym idzie, m - ax − b dla »adnej liczby x. Zatem
kongruencja (3.1) nie ma rozwi¡zania.
Przypu±¢my wi¦c, »e d ̸= 1 oraz d | b. Rozwa»my kongruencj¦
Dowód.
Skoro
(a
)
a
b
x≡
d
d
(mod
m
)
d
(3.3)
= 1, wi¦c kongruencja (3.3) ma rozwi¡zanie x0 . Zapiszmy
− =
dla pewnej liczby caªkowitej k . Mno»¡c obie strony tego
równania przez d otrzymujemy, »e x0 jest rozwi¡zaniem kongruencji (3.1).
Ale x0 jest rozwi¡zaniem (3.3), a ka»de dwie liczby speªniaj¡ce t¦ kongruencj¦ ró»ni¡ si¦ o wielokrotno±¢ md . Zatem w Zm jest tych rozwi¡za«
dokªadnie d i ka»de z nich mo»emy zapisa¢ w postaci x0 + md i mod m dla
i ∈ {0, 1, . . . , d − 1}. S¡ to wi¦c wszystkie rozwi¡zania kongruencji (3.1).
a
x
d 0
NWD
b
d
d
m
d
m
k
d
,
Tak wi¦c kongruencja z przykªadu 3.7 ma dokªadnie jedno rozwi¡zanie.
Podamy jeszcze jeden przykªad ilustruj¡cy powy»sze twierdzenie.
3.9 Przykªad. Rozwi¡»emy kongruencj¦
Poniewa»
NWD(4, 30) = 2 oraz 2 | 10, wi¦c nasza kongruencja ma dwa rozwi¡zania. Redukujemy caª¡ kongruencj¦ przez 2 otrzymuj¡c 2x ≡ 5 (mod 15), a nast¦pnie
znajdujemy liczb¦ odwrotn¡ do 2 modulo 15. jest ni¡ 8. Otrzymujemy wi¦c
x0 = 10. Jest to pierwsze rozwi¡zanie. Drugim jest x1 = 10 + 15 = 25.
16
4x ≡ 10 (mod 30).