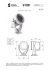Układy prądowe dokonujące konwersji liczb z - kik

Magdalena Rajewska
Oleg Maslennikow
Robert Berezowski
Wydział Elektroniki i Informatyki
Politechnika Koszalińska
ul. Śniadeckich 2, 75-453 Koszalin
[email protected]
[email protected]
[email protected]
Układy prądowe dokonujące konwersji liczb
z systemu binarnego do systemu RNS
i odwrotnie
Słowa kluczowe: bramki prądowe, resztowy system
wielowartościowa, arytmetyka resztowa, układy konwersji
liczbowy
RNS,
logika
STRESZCZENIE
W pracy przedstawiono metody konwersji liczb z systemu binarnego do systemu resztowego RNS
i odwrotnie. Zaprezentowano układy realizujące omawiane konwersje. Proponowane układy zostały zbudowane
w oparciu o bramki prądowe. Wyróżniającą cechą opracowanych układów jest znacznie mniejsza liczba
połączeń w porównaniu do konwerterów zbudowanych w oparciu o klasyczne bramki napięciowe. Do
zweryfikowania poprawności działania zaprojektowanych układów w środowisku ActiveHDL, stworzono
bibliotekę napisaną w języku opisu sprzętu VHDL. Zawiera ona opis podstawowych bramek prądowych
i elementów oraz tablicę rezolucji sygnałów prądowych.
1.
WPROWADZENIE
Resztowe systemy liczbowe RNS (ang. Residue Number System) stają się coraz
bardziej popularne ze względu na charakterystyczne właściwości, jakie są z nimi związane:
zrównoleglenie operacji, modułowość, brak przeniesienia pomiędzy cyframi. RNS dobrze
pasuje do systemów cyfrowego przetwarzania sygnałów (CPS), szczególnie do konstruowania
jednostek przetwarzających tych systemów. Ze względu na pewną złożoność systemów
resztowych pożądana jest konwersja z oraz do systemu dziesiętnego i binarnego. Oczywiście
ważne jest żeby konwersja ta była maksymalnie efektywna.
W 1998 roku na Politechnice Koszalińskiej opracowano pierwsze bramki prądowe [1],
w których poziomy logiczne odpowiadają ustalonym wartościom prądu. Od tego czasu
bramki te zostały poddane wielu modyfikacjom [2,3]. Obecnie zdefiniowana logika bramek
prądowych jest w pewnym stopniu logiką wielowartościową [3]. Dzięki tej właściwości
bramek prądowych możliwe jest konstruowanie układów cyfrowych działających w logice
wielowartościowej z podstawą N>2 lub w arytmetyce resztowej (opartej o arytmetykę
modulo N). Wartość zmiennej albo funkcji logicznej Y na wyjściu dowolnej bramki prądowej
należy do zbioru Y∈{-N, N}, natomiast wartość zmiennej (albo funkcji) logicznej, która może
się pojawić na wejściu bramki, np. jako wynik operacji dodawania lub odejmowania prądów,
teoretycznie należy do przedziału (-L, R). Dodatkową wyróżniającą cechą bramek prądowych
IX Projekty finansowane przez MNiI
— 591 —
jest stała wartość prądu pobieranego ze źródła zasilania w różnych trybach ich pracy
(np. w stanach logicznego zera i jedynki). Z tego powodu cechują się one znacznie mniejszym
poziomem pasożytniczych sprzężeń podłożowych, stąd w mniejszym stopniu (do 10 razy,
w zależności od wartości prądu odpowiadającego jedynce logicznej, i od wymaganej
szybkości działania) zakłócają układy analogowe w porównaniu z układami napięciowymi.
Oprócz tego, wcześniejsze badania sposobów projektowania cyfrowych układów
prądowych [1] wykazały, że standardowe układy cyfrowe (np. sumatory, multipleksery,
dekodery, bloki operacyjne ALU, liczniki itd.) zbudowane w oparciu o bramki prądowe są
prostszymi logicznie (pod względem ilości wykorzystanych bramek do 35%) od ich
prototypów zbudowanych w oparciu o klasyczne bramki napięciowe [4].
X
Y1
Y2
Y3
Y4
X
I
Y1
AI
Y2
K1
X
K1
I
I
I
AI
4
Y3
AI
X
K2
I
K3
I
Y1
Y2
AI
AI
Y4
Rys. 1. Przykładowa realizacja wielowyjściowej
bramki prądowej (N=2)
Y1
Y2
I
Rys. 2. Przykładowa realizacja dwuwyjściowej bramki
prądowej (N=4)
Charakterystyczną cechą budowy bramek prądowych jest modułowość i regularność ich
budowy. Oznacza to, że schemat bramki składa się z prostych bloków kilku różnych typów,
mianowicie bloków K, I i AI, których liczba zależy od wartości podstawy N systemu
liczbowego. Każda bramka zawiera obwod wejściowy przedstawiający sobą N-1 szeregowo
połączonych komparatorów K oraz jednego lub kilku (w zależności od liczby wyjść bramki)
obwodów wyjściowych typu inwerter I lub anty-inwerter AI. Przykład realizacji bramki
prądowej z wyjściami wszystkich czterech typów (inwerter, anty-inwerter, podwójny
inwerter, anty-podwójny inwerter) przedstawiono, dla N=2, na rys. 1. W przypadku większej
wartości N, realizacja jednego wyjścia typu inwerter wymaga podłączenia osobnego bloku I
do wyjścia każdego komparatora K. Wyjścia wszystkich (N-1) bloków I są połączone w jeden
węzeł reprezentujący wyjście bramki. Sposób realizacji bramki z wyjściem typu inwerter
i wyjściem typu anty-inwerter przedstawiono (dla N=4) na rys. 2. Szczegółowy opis bramek
prądowych przedstawiony jest w pracy [3].
2.
SYSTEM RESZTOWY RNS
W arytmetyce modulo N zapis liczby jest uzależniony od podstawy N systemu
i pozwala na przedstawienie w sposób jednoznaczny N-1 liczb. Zapis większych od podstawy
systemu N liczb sprowadza się do wyliczenia reszty z dzielenia tej liczby przez jego
podstawę. Ważną zaletą arytmetyki modulo N jest brak przeniesienia przy wykonywaniu
operacji dodawania, odejmowania i mnożenia.
System resztowy używa G pojedynczych arytmetyk modulo Nj, pozwalając na
jednoznaczny zapis liczb z zakresu od 0 do N1 * N2…Nj (j=1,2,…,G). Przykładowo liczba
1710 zapisana w 3-cyfrowym (G=3) systemie resztowym RNS(N1|N2|N3)=RNS(5|3|2) będzie
oznaczona jako (2|2|1)RNS(5|3|2). Jednoznacznie dla tego przykładu możemy zapisać liczby
z zakresu od 0 do (2*3*5-1=29). Istotnym elementem jest dobór poszczególnych podstaw
w systemie resztowym. Powinien on spełniać dwa warunki: pozwolić na objęcie swoim
zakresem całego zbioru liczb, na którym operuje system CPS oraz podstawy powinny
spełniać warunek: NWW(Ni,Nj)=Ni▪Nj (najmniejsza wspólna wielokrotność każdej pary liczb
reprezentujących podstawy systemów jest równa iloczynowi tych liczb). Ze względu na brak
przeniesienia przy wykonywaniu podstawowych operacji arytmetycznych, wykonywane one
mogą być równolegle na wszystkich cyfrach systemu, niezależnie od siebie. Zwiększa to
szybkość działania układu, głównie tam gdzie wykorzystywane są podstawowe operacje
— 592 —
matematyczne (filtry cyfrowe, FFT). Przykładowo dodając liczbę 17 do liczby 4 otrzymujemy
(2|2|1)RNS(5|3|2)+(4|1|0)RNS(5|3|2)=(1|0|1)RNS(5|3|2), odpowiednio modyfikując poszczególne cyfry
wyniku, które przekraczają określoną podstawę systemu.
3.
MODELOWANIE UKŁADÓW PRĄDOWYCH
Rosnąca liczba bramek prądowych w realizowanych układach wymaga środowiska,
w którym można realizowany układ testować. Język VHDL został stworzony przede
wszystkim do opisu cyfrowych układów w technologii napięciowej. Biblioteka IEEE1164
(jest ona elementem składowym symulatora ActiveHDL) zawiera opis VHDL podstawowych
bramek napięciowych i określa 9 poziomów logicznych w pełni opisujących standardową
logikę binarną. W celu testowania układów zbudowanych w oparciu o bramki prądowe
opracowano bibliotekę nstd_logic_2003 [5]. Wprowadzenie większej liczby poziomów oraz
nowych elementów związanych z systemami resztowymi o podstawach większych niż 10
wymusiło stworzenie nowej wersji biblioteki o nazwie current_pk. W bibliotece
zadeklarowano wartości od „m30” do „p30” odpowiadające poziomom logicznym od -30 do
+30 oraz tablicę rezolucji sygnałów (Tab. 1) z uwzględnieniem algebry prądowej.
Tabela 1. Przykładowy wycinek tablicy rezolucji sygnałów w algebrze prądowej z biblioteki current_pk
U X m3 m2 m1 p0 p1 p2 P3
U U U U U U U U U U
X U X X X X X X X X
m3 U X m6 m5 m4 m3 m2 m1 p0
m2 U X m5 m4 m3 m2 m1 p0 p1
m1 U X m4 m3 m2 m1 p0 p1 p2
p0 U X m3 m2 m1 p0 p1 p2 p3
p1 U X m2 m1 p0 p1 p2 p3 p4
p2 U X m1 p0 p1 p2 p3 p4 p5
p3 U X p0 p1 p2 p3 p4 p5 p6
Poszczególne poziomy określają wartość
przez węzeł.
4.
U – poziom logiczny niezainicjowany
X – poziom logiczny sygnalizujący błąd
m3 – poziom logiczny minus „3”
m2 – poziom logiczny minus „2”
m1 – poziom logiczny minus „1”
p0 – poziom logiczny „0”
p1 – poziom logiczny „1”
p2 – poziom logiczny „2”
p3 – poziom logiczny „3”
i kierunek natężenia prądu przepływającego
KONWERSJA LICZB Z SYSTEMU BINARNEGO DO SYSTEMU
RESZTOWEGO
Konwersja P-bitowej liczby binarnej Y = ( yP −1 , yP − 2 ,..., y0 ) BIN do systemu RNS
X = ( xG , xG −1 ,..., x1 ) RNS wyrażona jest wzorem (1):
xj = (yP−1, yP−2 ,...,y0 )BIN N = yP−12P−1 + yP−2 2P−2 +...+ y0 20
j
gdzie reszta: x j = Y
Nj
= Y mod N j
Nj
= yP−12P−1 + yP−2 2P−2 + y0 20
Nj
Nj
Nj
(1)
Nj
(2)
Na rys. 3 przedstawiono ogólny schemat układu do konwersji liczb z systemu binarnego
na system modulo Nj. Kolejne bity liczby binarnej Y = ( yP −1 , yP − 2 ,..., y0 ) BIN sterują
buforami B, które przekazują stałe |2p-1|Nj , |2p-2|Nj,…,|20|Nj na wejścia sumatorów ΣmodNj.
Np., jeżeli na wejściu yi pojawi się wartość „1” bufor B przekaże wartość odpowiedniej stałej
|2i|Nj do układu sumatorów modulo Nj. Tab. 2 zawiera wartości stałych |2i|Nj dla różnych
podstaw Nj, które zostały wyznaczone na podstawie wzoru (1). W przypadku konwersji
P-bitowej liczby binarnej do G-cyfrowego systemu RNS o podstawach N1,..., NG wymagane
jest wykorzystanie G niezależnie działających układów konwertera (przedstawionego na
IX Projekty finansowane przez MNiI
— 593 —
Tabela 2. Pomocnicza tabela do konwersji liczb z systemu
binarnego na system resztowy
Nj
2
3
5
7
9
11
13
17
0
1
2
3
4
5
6
7
y0
|20|Nj
8
y1
y2
yg-1
B
∑
∑
|2 |Nj |2 |Nj |2 |Nj |2 |Nj |2 |Nj |2 |Nj |2 |Nj |2 |Nj |2 |Nj |2 |
B
1
0
0
0
0
0
0
0
0
|2 |
B
1
2
1
2
1
2
1
2
1
∑
1
2
4
3
1
2
4
3
1
(X) mod Nj
|2 |
B
1
2
4
1
2
4
1
2
4
1
2
4
8
7
9
1
2
4
P buforów
P-1 sumatorów mod Nj
1
2
4
8
5
10 9
7
3 Rys. 3. Ogólny schemat konwertera liczb
1
2
4
8
3
6
12 11 9
z systemu binarnego do liczb
w arytmetyce resztowej modulo Nj
1
2
4
8
16 15 13 9
1
Mod
Nj
1
Mod
Nj
Nj
2
Nj
Mod
Nj
n-1
Nj
rys.3), w których sumatory resztowe muszą działać w arytmetyce z odpowiednią podstawą Nj.
Rys.4 zawiera przykładowy schemat konwertera 6-bitowych liczb binarnych do systemu
resztowego RNS(7|3|2). Składa się on z trzech niezależnych od siebie konwerterów (schemat
ogólny pojedynczego konwertera pokazano na rys. 3). Wartości na wejściach |2p-1|Nj ,
|2p-2|Nj,…,|20|Nj oraz układy sumatorów modulo Nj zostały dostosowane do odpowiednich
arytmetyk modulo Nj (N3=7, N2=3, N1=2), z których składa się prezentowany system resztowy
Ze względu na charakterystyczne wartości w Tab. 2 dla arytmetyki modulo 2 (podobnie dla
arytmetyk: modulo 4, modulo 8, itd.) schemat konwertera został uproszczony i składa się
jedynie z bufora. Schematy sumatorów modulo Nj przedstawione zostały na rys. 5, 6. Na
rys. 7 przedstawiono wyniki symulacji opisanego powyżej konwertera. Zgodnie z założeniem
jednoznacznie można określić wartość z zakresu od 0DEC do 41DEC. Dla wartości 42DEC na
wyjściu pojawia się wartość (0|0|0)RNS(7|3|2), która odpowiada wartości 0DEC.
y0
1
1
(x1)N=2
B
B
ADDRNS3
B
1
ADDRNS3
(x2)N=3
ADDRNS3
y1
2
B
B
2
3
ADDRNS7
y2
1
B
ADDRNS3
B
4
-2
ADDRNS7
ADDRNS7
(x3)N=7
y3
2
B
B
1
ADDRNS7
y4
1
B
Rys. 5. Sumator resztowy modulo 3
– ADDRNS3
7
ADDRNS3
B
2
-6
y5
2
4
B
B
ADDRNS7
Rys. 4. Konwerter liczb z systemu binarnego do systemu resztowego
RNS(7|3|2) zbudowany w oparciu o bramki prądowe
Rys. 6. Sumator resztowy modulo 7
– ADDRNS7
Rys. 7. Wyniki symulacji konwertera liczb z systemu binarnego do RNS(7|3|2) w środowisku ActiveHDL
— 594 —
5.
KONWERSJA LICZB Z SYSTEMU RESZTOWEGO DO SYSTEMU
BINARNEGO
W literaturze [6] opisane są dwa sposoby konwersji liczb z systemu resztowego do
systemu binarnego. Jedna z metod oparta jest na przejściowej konwersji do systemu MRS
(Mixed Radix form System), a następnie do systemu binarnego. Druga metoda wykorzystuje
Chińskie twierdzenie o resztach (CRT).
Do projektowania konwertera wykorzystano pierwszą metodę. Konwersja liczb
z systemu RNS do systemu dziesiętnego sprowadza się do wyznaczenia odwrotności
multiplikatywnej αj (3) dla każdej podstawy systemu Nj.
⎛
⎞
⎜α j ⋅ N ⎟ = 1 ,
⎜
N j ⎟⎠
⎝
Nj
(3)
G
gdzie N = ∏ N j , Nj – podstawa j-tej cyfry układu RNS.
j =1
Liczbę w kodzie dziesiętnym można obliczyć korzystając ze wzoru (4):
G ⎛
N ⎞⎟
DEC = ∑ ⎜ x j ⋅ α j ⋅
⎜
N j ⎟⎠
j =1 ⎝
N
(4)
Przykładowo podano obliczenia dla systemu RNS(5|3).
N1 = 5, N 2 = 3 → N = 15
⎛
N⎞
⎜⎜ α1 ⋅ ⎟⎟ = 1 → α1 = 2 ,
N1 ⎠ N
⎝
1
DEC = x2 ⋅ α 2 ⋅
⎛
N ⎞
⎜⎜ α 2 ⋅
⎟ = 1 → α2 = 2 .
N 2 ⎟⎠ N
⎝
2
N
15
15
N
+ x1 ⋅ α1 ⋅ = x2 ⋅ 2 ⋅ + x1 ⋅ 2 ⋅ = 6 ⋅ x2 + 10 ⋅ x1
n2
n1
5
3
(5)
Wykorzystując wzór (5) zaprojektowano konwerter liczb z systemu RNS(5|3) do
systemu dziesiętnego zbudowanego w oparciu o bramki prądowe (rys. 10). Schemat
konwertera jest praktyczną realizacją wzoru (5). Składa się z układów mnożących oraz
układów sumatorów (rys. 11) działających w arytmetyce resztowej modulo N (w omawianym
przykładzie N=N1*N2=15). Wyniki symulacji przedstawione są na rys. 8.
Drugim etapem jest konwersja liczb z systemu dziesiętnego na liczbę w systemie
binarnym. Przykładowa realizacja konwertera pokazana jest na rys. 14. Wadą tego układu jest
czas propagacji sygnału wejściowego zależny od ilości bitów. Wyniki symulacji
przedstawione są na rys. 9.
Rys. 8. Wyniki symulacji układu konwertującego liczbę z systemu resztowego RNS(5|3) do systemu
dziesiętnego
Rys. 9. Wyniki symulacji układu konwertującego liczbę z systemu dziesiętnego do systemu binarnego
IX Projekty finansowane przez MNiI
— 595 —
(x 1) N=3
S
3
K0
-14
K1
B
10
15
IN1+IN2
B
10
ADDRNS15
ADDRNS15
DEC
15
Rys. 11. Sumator resztowy modulo 15 –
ADDRNS15
S
(x 2)N=5
IN1+IN2
5
-1
K0
6
K1
K2
K3
B
Rys. 12. Sumator wielowartościowy
o podstawie 2- ADDMVL2
ADDRNS15
B
6
S
B
6
-3
Rys. 10. Konwerter liczb z systemu RNS(5|3) do systemu
dziesiętnego zbudowany w oparciu o bramki prądowe
ADDMVL2
ADDMVL4
ADDMVL8
y0
C
Rys. 13. Sumator wielowartościowy
o podstawie 4- ADDMVL4
S
IN1+IN2
8
y1
y2
-7
y3
Rys. 14. Konwerter liczb z systemu dziesiętnego do systemu
binarnego zbudowany w oparciu o bramki prądowe
6.
4
IN1+IN2
B
6
DEC
C
C
Rys. 15. Sumator wielowartościowy
o podstawie 8- ADDMVL8
WNIOSKI
W pracy zaprezentowano układy zbudowane z bramek prądowych, konwertujące liczby
z systemu binarnego na system resztowy i odwrotnie. Zaprezentowano bibliotekę napisaną
w języku opisu sprzętu VHDL, którą wykorzystano do symulacji zaprojektowanych układów
w środowisku ActiveHDL. Wyniki symulacji potwierdziły poprawność działania układów.
Otwartym problemem zostaje minimalizacja czasu opóźnienia układu konwertera
z systemu dziesiętnego na system binarny.
BIBLIOGRAFIA
[1] D. Gretkowski, R. Berezowski, N. Maslennikowa, „Opis i modelowanie cyfrowych układów prądowych
z wykorzystaniem języka VHDL”, Mat. II Konferencji Krajowej “Reprogramowalne układy cyfrowe”,
RUC’99, Szczecin 1999, str. 165-172
[2] Maslennikow O., Gretkowski D., Pawłowski P. „Current-Mode Circuits for Multiple- Valued Logic and
Residue Number System Arithmetic”, Proc. of the 10-th Int. Conf. on Mixed Design, MIXDES’2003,
pp. 182-187
[3] O. Maslennikow, „Podstawy teorii zautomatyzowanego projektowania reprogramowalnych równoległych
jednostek przetwarzających dla jednoukładowych systemów czasu rzeczywistego”, Wydawnictwo
Uczelniane Politechniki Koszalińskiej, Koszalin 2004, pp. 148-196
[4] W. Traczyk, “Układy cyfrowe. Podstawy teoretyczne i metody syntezy”, WNT Warszawa, 1986
[5] M. Białko, M. Rajewska, R. Berezowski, „Wykorzystanie języka VHDL do modelowania układów
pracujących w logice wielowartościowej i w arytmetyce resztowej”, Prace X Konferencji Krajowej
„Komputerowe wspomaganie badań naukowych”, KOWBAN’2003
[6] S. J. Piestrak, „Design of High-Speed Residue-to-Binary Number System Converter Based on Chinese
remainder theorem”, Proc. ICCD’94, Int. Conf. on Computer Design: VLSI in Computers and Processors,
Cambridge, MA Oct. 10-12.1994, pp. 508-511
Praca jest wykonana w ramach grantu KBN 3T11B05926
— 596 —