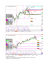PDF file

Wyznaczenie charakterystyk
statystycznych modelu DLL
(Dynamic Lattice Liquid) dla
układów stopów polimerowych
Model DLL to model sieci, gdzie węzły są zajęte przez
elementy kinetyczne (koraliki) drgające z określoną
częstotliwością termiczną.
Warunek ciągłości masy: wszystkie
węzły sieci są zajęte przez koraliki
∂ρ/∂t + ∇ J = 0
Układ polimerowy - koraliki połączone
nierozerwalnymi wiązaniami odpowiadającymi
łańcuchowi głównemu polimeru. W układach
rozcieńczonych - pojedyncze koraliki
odpowiadają cząsteczkom rozpuszczalnika.
Algorytm ruchu kooperatywnego
1. tworzenie pola wektorowego reprezentującego próby ruchu
2. eliminacja nieskutecznych prób
3. kooperatywne przesunięcie koralików wzdłuż zamkniętych
pętli.
4. rejestracja aktualnej konfiguracji
Procedura ta rozpatrywana jest w pojedynczych krokach
czasowych τ ν z częstością odpowiadającą średniej częstości
drgań termicznych (ν= 1/τ ν).
Algorytm jest dokładnie powtarzany w kolejnych krokach
czasowych z nowym losowym polem kierunków prób.
Koraliki, które nie wnoszą udziału do kooperatywnych ruchów nie są
przesuwane, tj. w przypadkach:
(1) ruch dwóch sąsiednich koralików w kierunku do siebie
(2) ruch w przypadku, gdy żaden z sąsiednich koralików nie wykonuje ruchu
na jego miejsce
(3) ruch prowadzący do zerwania łańcucha polimeru
Dosem.exe
Prawdopodobieństwo, że element kinetyczny bierze udział w
n-elementowej pętli
M
P( n ) =
∑ N ( n)
i =1
i
M ⋅R
gdzie: M- ilość losowań, R-ilość koralików w matrycy
Prawdopodobieństwo, że element kinetyczny zostanie
przesunięty
nmax
Ptot = ∑ n ⋅ P( n )
n =3
Łańcuchy 20 matryca 40x40
Ptot
0,0022
0,002
0,0018
automat
0,0016
ręcznie
0,0014
0,0012
0,001
0
200000
400000
600000
800000
czas
1000000 1200000 1400000
Łańcuchy 20
0,0021
0,002
0,00195
0,002
0,0019
Matryca 80x80
Matryca 100x100
0,00185
0,0019
0,0018
0,00175
0,0018
0,0017
0,0017
0,00165
0,0016
0,0016
0,00155
0,0015
0,0015
0
50000
100000
150000
200000
250000
300000
350000
0
400000
50000
100000
150000
200000
250000
300000
350000
400000
Łańcuchy 40
0,0021
0,0021
0,002
0,002
Matryca 80x80
0,0019
0,0019
0,0018
0,0018
0,0017
0,0017
0,0016
0,0016
Matryca 120x120
0,0015
0,0015
0
50000
100000
150000
200000
250000
300000
0
50000
100000
150000
200000
250000
P( n ) = Bn µ
−h
B. D. Hughes,
n
Random Walk and Random
Environments
(Clarendon, Oxford,1995)
B – stała zależna od sieci
µ – efektywna liczba koordynacyjna
h – wykładnik
0
-2 2
-4
3
4
5
6
7
8
9
10 11 12 13 14 15 16
n
N=20
-6
N=40
-8
ln(P(n))
h = 2,93
N=10
B = 1,07
Polan
-10
µ = 0,71
-12
-14
-16
-18
-20
-22
-24
0
20
n 40
60
0
100
200
rozmiar
300
Pojedyncze kulki
Łańcuchy o długości 20
h = 2,93
5
B = 1,07
4,5
µ = 0,71
4
3,5
B
h
3
2,5
µ
2
Łańcuchy
h = 4,01
1,5
B = 0,63
1
µ = 0,39
0,5
0
0
20
40
60
rozmiar matrycy
80
100
120
łańcuchy o długości 40
4,5
4
3,5
3
B
h
2,5
µ
2
1,5
1
0,5
0
0
20
40
60
rozmiar matrycy
80
100
120
Funkcja autokorelacji pozycji segmentu (ρ s) charakteryzuje lokalną ruchliwość układów
N
1
ρ S (t ) =
ci (t )ci (0)
∑∑
Nn n i
Gdzie ci = 1 dla elementu kinetycznego przyjmującego tę samą pozycję w czasie t=0 i t oraz
ci = 0 kiedy element kinetyczny jest przesunięty z pozycji zerowej
(N=długość łańcucha, n=ilość łańcuchów w układzie),
ρ R (t ) = A exp(−
Matryca 80x80
t
τ R1
) + B exp(−
t
τ R2
)
Czas relaksacji łańcuchów:
1
1
t
2
ρ R (t ) = ∑ Rn (t0 ) ⋅ Rn (t ) = ∑ Rn (t0 ) ⋅ exp(− )
n n
n n
τR
gdzie R są wektorami koniec-koniec łańcucha w chwili t=t0 i t
1
2
< r (t ) >= ∑ [ rcm (t ) − rcm (t0 )] = 4 Dt
n n
2
0,06
0,05
0,04
0,03
y = 1E-06x
R2 = 0,9588
0,02
0,01
0
0
5000
10000
15000
20000
25000
30000
35000
40000
45000
50000