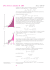Co można, a czego nie można zrobić z nierównością i

Co można, a czego nie można zrobić z nierównością i dlaczego?
Każda operacja na nierówności to tak naprawdę jedno z dwojga:
1. „zadziałanie” na obydwie strony nierówności pewną funkcją, albo
2. opuszczenie po obydwu stronach nierówności znaku pewnej funkcji.
Powyższe zdanie dotyczy wszystkich operacji wykonywanych na nierównościach, także tych,
które uczeń poznaje już w szkole podstawowej i gimnazjum, jak pomnożenie obydwu stron
nierówności przez liczbę różną od zera, czy dodanie do obydwu stron nierówności dowolnego
wyrażenia.
Przykłady:
3
Mamy równanie: (LewaStrona ) < (Pr awaStrona )
Równanie ma postać f (LewaStrona ) < f (Pr awaStrona ) , gdzie f ( x ) = x 3
Opuszczając znak tej funkcji otrzymujemy: LewaStrona < Pr awaStrona
Mamy równanie: LewaStrona < Pr awaStrona
Działając na obydwie strony równania funkcją f ( x) = 5x otrzymujemy:
f (LewaStrona ) = f (Pr awaStrona ) , tzn.
5 ⋅ LewaStrona < 5 ⋅ Pr awaStrona
Zadziałanie na obydwie strony równania podaną funkcją, to pomnożenie obydwu stron przez
liczbę 5.
3
Niektóre z takich operacji wykonywanych na nierównościach są poprawne, tzn. po ich
wykonaniu nie zmieni się zbiór rozwiązań nierówności (mówimy wtedy, że otrzymaliśmy
nierówność równoważną nierówności wyjściowej).
Niektóre jednak zmieniają zbiór rozwiązań – tych nie należy wykonywać.
Przykład użycia błędnej operacji
Nierówność wyjściowa: x < 2
Zbiorem rozwiązań tej nierówności jest przedział (− ∞ , 2) .
Bierzemy funkcję f ( x ) = x 2 i wykonujemy operację f ( x) < f ( 2) , w efekcie czego
otrzymamy: x 2 < 4 .
Zbiorem rozwiązań tej ostatniej nierówności jest przedział (− 2 , 2) , czyli zbiór rozwiązań
nierówności zmienił się.
Sztuka rozwiązywania nierówności polega więc na wykonywaniu na nich takich
operacji, które nie zmieniają zbioru rozwiązań, a jedynie zmieniają postać nierówności –
najlepiej w kierunku jej maksymalnego uproszczenia.
Powstaje pytanie: które operacje są dopuszczalne, a które nie?
Odpowiedź na to pytanie jest ukryta w definicji funkcji monotonicznych:
„Funkcję f(x) nazywamy rosnącą, jeżeli dla dowolnych argumentów x 1 , x 2 zachodzi:
x 1 < x 2 ⇔ f (x 1 ) < f (x 2 ) ”,
„Funkcję f(x) nazywamy malejącą, jeżeli dla dowolnych argumentów x 1 , x 2 zachodzi:
x 1 < x 2 ⇔ f (x 1 ) > f (x 2 ) ”.
Jak widać w definicjach tych wyraźnie zapisano, że jeżeli funkcja jest rosnąca, to
nierówności f (x 1 ) < f (x 2 ) oraz x 1 < x 2 są równoważne (czytaj: mają taki sam zbiór
rozwiązań).
Jeżeli natomiast funkcja jest malejąca, to nierówności f (x 1 ) > f (x 2 ) oraz x 1 < x 2 są
równoważne (czytaj: mają taki sam zbiór rozwiązań).
Nie zmieniamy więc zbioru rozwiązań nierówności w dwóch przypadkach:
1. Gdy zadziałamy na obydwie strony nierówności funkcją rosnącą (albo opuścimy
po obu stronach znak takiej funkcji).
2. Gdy zadziałamy na obydwie strony nierówności funkcją malejącą (albo opuścimy
po obu stronach znak takiej funkcji), zmieniając jednocześnie znak nierówności
na przeciwny.
W poniższej tabeli przedstawiono wykaz najczęściej używanych, poprawnych operacji na
równaniach:
Operacja
Podniesienie obydwu stron
nierówności do nieparzystej
potęgi (albo opuszczenie po
obydwu stronach takiej potęgi)
Przykład
Uzasadnienie poprawności
x3 > 23
x>2
Funkcje f ( x ) = x 3 , f ( x ) = x 5 ,
Podniesienie obydwu stron
nierówności do parzystej potęgi
(albo opuszczenie po obydwu
stronach takiej potęgi), lecz
jedynie w przypadku , gdy:
---obydwie strony nierówności
są nieujemne, albo
--- obydwie strony nierówności
są niedodatnie (tu będzie
zmiana znaku nierówności na
przeciwny)
x 2 + 3 ≤ 2x 2 + 1
f ( x ) = x 7 ,... są rosnące
obydwie strony nierówności są
nieujemne, więc:
(x
2
+3
)
2
jest parzyste
≤ 2x 2 + 1
− 3 > − 2x 2 + 8
obydwie strony nierówności są
niedodatnie, więc:
(− 3)2 < (−
2x 2 + 8
)
2
x 5 ≥ −32
Pierwiastkowanie obydwu stron
nierówności pierwiastkiem
stopnia nieparzystego
5
x 5 ≥ 5 − 32
x ≥ −2
x 4 > 16
jak
Logarytmowanie obydwu stron
nierówności (lub opuszczenie
logarytmów po obydwu
stronach), gdy obydwie strony
nierówności są dodatnie
Malejące są funkcje:
f ( x ) = x n , x ∈ − ∞ ,0 , gdy n
(
jest parzyste
Funkcje f ( x ) = n x ,
n ∈ {3,5,7,9,...}
są rosnące
x 4 > 4 16
>
Pierwiastkowanie obydwu stron
x >2
nierówności pierwiastkiem
stopnia parzystego, lecz tylko
x > 2 lub x < −2
wtedy, gdy obydwie strony
Uwaga: 4 x 4 = x , podobnie
nierówności są nieujemne
4
Rosnące są funkcje:
f ( x ) = x n , x ∈ 0, ∞ ) , gdy n
Funkcje f ( x ) = n x , x ≥ 0 ,
n ∈ {2,4,6,8,...}
są rosnące
x2 = x
log 3 (x − 2) < log 3 8
Dziedzina równania: x > 2
Opuszczamy logarytmy:
x−2<8
Wszystkie funkcje
logarytmiczne o podstawie
większej od 1 są rosnące.
Wszystkie funkcje
logarytmiczne o podstawie z
przedziału (0 , 1) są malejące.
Opuszczenie znaku funkcji
wykładniczej lub użycie tej
funkcji
(0,5)
> (0,5)
4x − 2 < 3
4x−2
3
Wszystkie funkcje wykładnicze
o podstawie większej od 1 są
rosnące. Wszystkie funkcje
wykładnicze o podstawie z
przedziału (0 , 1) są malejące.
Parę przykładów błędnych operacji na nierównościach:
Operacja
Przykład
Uzasadnienie
x2 + 1 < x − 1 / 2
x 2 + 1 < ( x − 1) 2
x 2 + 1 < x 2 − 2x + 1
2x < 0
x<0
Podniesienie obydwu stron
Wynik jest błędny, gdyż dla
nierówności do potęgi
liczb x < 0 lewa strona
parzystej, bez badania znaku
nierówności jest nieujemna, a
obydwu stron nierówności
prawa strona – ujemna.
Liczba nieujemna nie może
być mniejsza od liczby
ujemnej, czyli żadna z liczb
x < 0 nie jest rozwiązaniem
nierówności
π
sin x ≤ sin
2
π
x<
2
Opuszczenie znaku funkcji
π
trygonometrycznej
sin = 1 , a wiadomo, że
2
sin x ≤ 1 dla wszystkich liczb
rzeczywistych. Rozwiązanie
jest błędne.
Funkcja f ( x ) = x 2 nie jest
rosnąca
Funkcje trygonometryczne
nie są monotoniczne.
Rozwiążemy teraz przykładowe zadanie z wykorzystaniem omówionych zasad rządzących
rozwiązywaniem nierówności.
4−x > x−2
Wyznaczamy dziedzinę nierówności:
4−x ≥ 0 ⇔ x ≤ 4
Dla x ∈ (− ∞ ,4 lewa strona nierówności jest nieujemna.
Co natomiast dzieje się z prawą stroną?
x − 2 ≥ 0 ⇔ x ≥ 2 , czyli prawa strona nierówności jest nieujemna dla x ∈ 2,4 , natomiast
dla x < 2 jest ujemna.
Wobec tego w dziedzinie nierówności obydwie strony nierówności nie są tego samego
znaku (obie nieujemne lub obie niedodatnie), więc nie można nierówności podnieść
obustronnie do kwadratu.
Wydaje się, że sytuacja jest bez wyjścia. Tak jest tylko pozornie – wystarczy bowiem
przeprowadzić następujące rozumowanie:
1. Dla x < 2
Lewa strona nierówności jest nieujemna, a prawa ujemna, czyli nierówność jest spełniona
(liczba nieujemna jest większa od liczby ujemnej). Dlatego te wartości x są rozwiązaniami
nierówności. Mamy już więc część zbioru rozwiązań: x ∈ (− ∞ , 2)
2. Dla x ∈ 2,4
Obie strony nierówności są nieujemne – można nierówność podnieść obustronnie do
kwadratu:
(
)
4 − x > (x − 2)
Pamiętamy jednak, że te obliczenia dotyczą tylko liczb z przedziału 2,4
2
2
4 − x > x 2 − 4x + 4
x 2 − 3x < 0
x( x − 3) < 0
Rozwiązaniem tej nierówności kwadratowej jest: x ∈ (0 , 3) .
Ponieważ rozpatrujemy przedział 2,4 , więc rozwiązaniem przypadku 2 jest: x ∈ 2 , 3)
Ostatecznie rozwiązaniem nierówności jest zbiór: (− ∞ , 2) ∪ 2 , 3) = (− ∞ , 3)
Dla lepszej ilustracji tego zadania przedstawmy w jednym układzie współrzędnych wykresy
funkcji y = 4 − x oraz y = x − 2 :
Rozwiązując nierówność 4 − x > x − 2 , szukamy odpowiedzi na pytanie: dla jakich x
wykres funkcji y = 4 − x leży nad wykresem funkcji y = x − 2 .
Z wykresu odczytujemy, że dla x < 3 - takie właśnie rozwiązanie nierówności otrzymaliśmy.
autor: Tadeusz Socha
http://matura.webd.pl