porównanie metod aproksymacji pochodnych rozwiązań

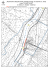
MODELOWANIE INŻYNIERSKIE
44, s. 29-36, Gliwice 2012
ISSN 1896-771X
PORÓWNANIE METOD APROKSYMACJI POCHODNYCH
ROZWIĄZAŃ OTRZYMYWANYCH ZA POMOCĄ METODY PURC
W ZAGADNIENIACH BRZEGOWYCH
AGNIESZKA BOŁTUĆ, EUGENIUSZ ZIENIUK
Wydział Matematyki i Informatyki, Uniwersytet w Białymstoku
e-mail: [email protected], [email protected]
Streszczenie. W pracy zaprezentowano technikę aproksymacji pochodnych
rozwiązań zagadnień brzegowych otrzymywanych za pomocą metody PURC.
Celem jej opracowania było uniknięcie obliczania tych pochodnych analitycznie
(co jest dość skomplikowane, a nawet niemożliwe) lub numerycznie w
konkretnych punktach (ze względu na czasochłonność i nieefektywność).
Efektywność zaproponowanej techniki polega na obliczaniu pochodnych w
sposób ciągły i w dowolnych punktach na brzegu oraz w obszarze za pomocą
otrzymanych szeregów aproksymujących. Wiarygodność i dokładność strategii
została przetestowana na przykładach z rozwiązaniami analitycznymi.
1. WSTĘP
Parametryczny układ równań całkowych (PURC) [4] jest metodą od lat rozwijaną jako
efektywna alternatywa dla klasycznych metod elementowych [2], służących do
rozwiązywania różnorodnych zagadnień brzegowych. Jego główne zalety to: brak
dyskretyzacji brzegu i obszaru modelowanego zagadnienia, wysoka dokładność
otrzymywanych rozwiązań oraz mniejsze wykorzystanie zasobów komputerowych. Zalety te
potwierdziły się, gdy wzięto pod uwagę przetestowane dotychczas zagadnienia brzegowe
modelowane różnymi równaniami różniczkowymi [4,5,6]. Pozostaje jednak wciąż szereg
problemów i pytań, na które należy odpowiedzieć, aby potwierdzić uniwersalność
i efektywność PURC w porównaniu z metodami klasycznymi.
Podobnie jak w przypadku klasycznych metod elementowych aktualnym problemem
pozostaje efektywne obliczanie pochodnych cząstkowych funkcji będących rozwiązaniem
zagadnienia brzegowego. Pochodne te są potrzebne w wielu zagadnieniach brzegowych, np.
w zagadnieniach teorii sprężystości do obliczenia odkształceń czy naprężeń. Potrzeba
obliczania pochodnych występuje też w wielu zagadnieniach dotyczących identyfikacji bądź
optymalizacji, a także w zagadnieniach plastycznych, co było głównym bodźcem do badań.
Przy ich rozpatrywaniu należy wielokrotnie obliczać naprężenia, które są niezbędne
w procesie iteracyjnym zastosowanym do rozwiązania tego typu zagadnień.
W przypadku klasycznych metod numerycznych problem ten był rozwiązywany różnymi
technikami. W MEB próbowano stosować różniczkowanie analityczne, w wyniku czego była
otrzymana tożsamość całkowa, która ostatecznie wymagała całkowania numerycznego w celu
obliczenia pochodnych w wybranych punktach obszaru. W zagadnieniach plastycznych
30
A. BOŁTUĆ, E. ZIENIUK
funkcje podcałkowe w tożsamości całkowej okazały się jednak silnie osobliwe, co znacząco
utrudniało proces obliczeniowy. Innym sposobem było bezpośrednie różniczkowanie funkcji
kształtu zastosowanych do aproksymacji rozwiązań na poszczególnych elementach.
Stosowano też numeryczne obliczanie pochodnych polegające na wykorzystaniu znanych
rozwiązań w blisko oddalonych od siebie punktach. Wspomniane techniki dają wartości
pochodnych w poszczególnych, wcześniej zadeklarowanych węzłach. Istnieje możliwość ich
bezpośredniego zastosowania także w metodzie PURC i zdaniem autorów mogą one być
skuteczne, jednak są też czasochłonne. Bardziej efektywnym i uniwersalnym sposobem
byłoby obliczanie pochodnych na podstawie bezpośredniego podstawienia punktów
(współrzędnych) do otrzymanych wyrażeń matematycznych aproksymujących pochodne
cząstkowe wymaganego rzędu.
Celem pracy jest uzyskanie matematycznych wyrażeń aproksymujących pochodne
cząstkowe pierwszego i drugiego rzędu. Zostały one otrzymane na bazie uogólnienia
wcześniej przetestowanych wyrażeń aproksymujących zastosowanych do uzyskania
rozwiązań (funkcji brzegowych) w metodzie PURC. Wyrażeniami tymi są uogólnione na
dwie zmienne szeregi aproksymujące, dające możliwość efektywnego obliczenia pochodnych
w obszarze i na jego brzegu. Ponadto wiarygodność otrzymanej aproksymacji przetestowana
została na konkretnych przykładach, a wyniki porównano z wynikami analitycznymi.
2. ALGORYTM APROKSYMACJI POCHODNYCH ROZWIĄZAŃ
Proponowana w pracy aproksymacja pochodnych rozwiązań bazuje na wykorzystaniu i
uogólnieniu na większą liczbę zmiennych szeregów (z funkcjami wielomianowymi)
stosowanych w PURC do aproksymacji rozwiązań na brzegu. W odróżnieniu od
wspomnianych szeregów będą to jednak szeregi zależne od dwóch zmiennych, a za ich
pomocą będą interpolowane rozwiązania na brzegu oraz w obszarze. W ich przypadku bez
problemów można analitycznie obliczyć pochodne wymaganego rzędu względem wszystkich
zmiennych. Ostatecznie otrzymuje się wyrażenie na podstawie którego, w sposób ciągły,
można wyznaczać pochodne rozwiązań w dowolnych punktach obszaru i brzegu.
Algorytm aproksymacji zademonstrowano na przykładach płaskich zagadnień teorii
sprężystości. Kolejne etapy realizacji omawianej techniki można opisać w sposób
następujący:
KROK 1: rozwiązanie PURC dla zadanego kształtu obszaru oraz warunków brzegowych i
uzyskanie rozwiązań na brzegu.
Sposób modelowania kształtu brzegu oraz numerycznego rozwiązywania PURC dla
zagadnień sprężystych opisano m.in. w [6].
KROK 2: uzyskanie rozwiązań w obszarze na podstawie tożsamości całkowej.
W przypadku prezentowanej techniki najważniejszym elementem jest wybranie
odpowiednich punktów z obszaru i/lub brzegu, na bazie których będą interpolowane
rozwiązania. Na podstawie otrzymanego wyrażenia będą następnie aproksymowane pochodne
w sposób ciągły w całym obszarze wraz z brzegiem. Rozmieszczenie wspomnianych punktów
ma istotny wpływ na dokładność dokonywanej aproksymacji.
KROK 3: zastosowanie odpowiedniego wariantu doboru punktów, w których uzyskujemy
rozwiązania (rozpatrywane warianty opisano ze szczegółami w punkcie 3. pracy).
KROK 4: wybranie i zastosowanie określonego wariantu rozmieszczenia punktów dobranych
do
otrzymania
rozwiązań
w
kroku
3.
KROK 5: uogólnienie szeregu interpolującego z jedną zmienną na szereg z dwiema
PORÓWNANIE METOD APROKSYMACJI POCHODNYCH ROZWIĄZAŃ OTRZYMYWANYCH … 31
zmiennymi; przykładowo w zagadnieniach płaskiej teorii sprężystości dla przemieszczeń u x
jest on przedstawiany w następującej postaci
k 1 k 1
S ux ( x, y )   a jk lT j ( x)Tl ( y ) ,
(1)
j 0 l 0
gdzie k jest liczbą punktów (pokazanych na Rys. 1a), w których brane są rozwiązania.
T j ( x), Tl ( y ) to dowolne wielomianowe funkcje bazowe. W pracy wykorzystano wielomiany
Czebyszewa I rodzaju, które są zdefiniowane w postaci rekurencyjnej [1]
T0 ( x )  1, T1 ( x)  x, T j ( x)  2 xT j 1 ( x )  T j  2 ( x),
(2)
zaś a j  k  l są niewiadomymi współczynnikami w szeregu S u x ( x, y ) (1). Wspomniane
współczynniki otrzymywane są na podstawie rozwiązania układu równań (3). Powstaje on w
wyniku zapisania szeregu (1) w odpowiednio dobranych i rozmieszczonych n  k 2 punktach
obszaru i/lub brzegu i przyrównaniu szeregów do rozwiązań w tych punktach (uzyskanych za
pomocą PURC i tożsamości całkowej)
 T0 ( x0 )T0 ( y0 ) ... T0 ( x0 )Tk 1 ( y0 ) ... Tk 1 ( x0 )T0 ( y0 ) ... Tk 1 ( x0 )Tk 1 ( y0 ) 
 T ( x )T ( y )
... T0 ( x1 )Tk 1 ( y1 )
... Tk 1 ( x1 )T0 ( y1 )
... Tk 1 ( x1 )Tk 1 ( y1 ) 
 0 1 0 1



...
...
...
...
...
...
...


T0 ( xn1 )T0 ( yn1 ) ... T0 ( xn1 )Tk 1 ( yn1 ) ... Tk 1 ( xn1 )T0 ( yn1 ) ... Tk 1 ( xn1 )Tk 1 ( y n1 )
, (3)
 a0   u x 0 ( x0 , y0 ) 
 a   u (x , y ) 
x1 1
1

 1   
 ...  

...

 

 an1  u xn1 ( xn1 , yn1 )
gdzie u x 0 ( x0 , y 0 ), u x1 ( x1 , y1 ),..., u xn1 ( x n1 , y n1 ) to wspomniane rozwiązania, w tym
przypadku są to wartości przemieszczeń u x uzyskane w n punktach ( xi , y i ), i  0,1,..., n  1 .
Zastosowanie tej techniki jest równoważne z otrzymaniem wyrażenia matematycznego
aproksymującego rozwiązania w obszarze i na brzegu. Innymi słowy otrzymano szereg
interpolujący rozwiązania, będący wielomianową funkcją dwóch zmiennych łatwo
różniczkowalną.
KROK 6: bezpośrednie zróżniczkowanie szeregów interpolujących rozwiązania względem
poszczególnych zmiennych w efekcie prowadzi do otrzymania szeregów aproksymujących
pochodne rozwiązań np.
Su x ( x, y ) k 1 k 1
 2 Su x ( x, y ) k 1 k 1
T j ( x )
 2T j ( x)
  a j  k  l
Tl ( y ),
  a j  k  l
Tl ( y ),
x
x
x 2
x 2
j 0 l 0
j 0 l 0
(4)
 2 S u x ( x , y ) k 1 k 1
T j ( x) Tl ( y )
  a j  k  l
.
xy
x
y
j 0 l  0
Za pomocą szeregów (4) można obliczyć pochodne rozwiązań w sposób ciągły w
dowolnych punktach obszaru i/lub brzegu. Niezbędne jest jednak wyznaczenie pochodnych
cząstkowych wielomianów Czebyszewa względem poszczególnych zmiennych. W tym celu
można wykorzystać następujące wzory rekurencyjne [1]
T j ( x)
 2T j ( x)
( j  1)T j ( x)  U j ( x)
 jU j 1 ( x),
 j
,
(5)
2
x
x
x2  1
gdzie T j (x ) - to wielomiany Czebyszewa I rodzaju, zaś U j (x) - to wielomiany Czebyszewa
II rodzaju [1].
32
A. BOŁTUĆ, E. ZIENIUK
Pokazany na przykładzie przemieszczeń u x algorytm może być stosowany analogicznie
dla dowolnych poszukiwanych rozwiązań.
3. TECHNIKI DOBORU I ROZMIESZCZANIA PUNKTÓW DO INTERPOLACJI
Jak już wspomniano we wcześniejszej części pracy, istotnym elementem algorytmu jest
odpowiednie dobieranie punktów, w których będą otrzymywane rozwiązania. W związku z
tym zachodziła potrzeba przetestowanie różnych wariantów, w zależności od potrzeb
związanych z rozpatrywanym zagadnieniem. W pracy zastosowano i przebadano trzy
warianty dobierania punktów, w których niezbędne są dyskretne rozwiązania do aproksymacji
pochodnych: 1) tylko w obszarze, 2) na brzegu i w obszarze, 3) tylko na brzegu. Wariant
trzeci był wprowadzony na potrzeby aproksymacji pochodnych jedynie na brzegu. Biorąc pod
uwagę dwa pozostałe warianty możliwym jest otrzymywanie pochodnych rozwiązań w
dowolnych punktach obszaru i brzegu. Warto jednak podkreślić, iż w przypadku
rozpatrywania punktów tylko z obszaru, pochodne na brzegu otrzymujemy w wyniku
ekstrapolacji.
Kolejnym problemem było zastosowanie odpowiedniej techniki rozmieszczania punktów
w ramach wybranego, opisanego powyżej wariantu ich dobierania. Powstawało pytanie czy
będzie to miało wpływ na dokładność uzyskiwanych wartości pochodnych. W pracy wybrano
i zbadano trzy warianty rozmieszczenia punktów zaprezentowane na rys.1 (na przykładzie
n  81 dla 1 wariantu doboru punktów). Początkowo punkty rozmieszczono w sposób
najbardziej intuicyjny, a mianowicie równomiernie (rys.1a). Następnie rozpatrywano
rozmieszczanie punktów w miejscach odpowiadających miejscom zerowym wielomianów
Czebyszewa I rodzaju n-tego stopnia (rys.1b). Takie rozmieszczenie jest znane jako
optymalne rozmieszczenie punktów w jednowymiarowych zagadnieniach interpolacji,
pozwalające na uniknięcie efektu Rungego. Jako trzeci wariant wybrano rozmieszczenie
punktów w węzłach odpowiadających pierwiastkom wielomianu Legendre’a n-tego stopnia
(rys. 1c).
a)
b)
c)
Rys.1. Warianty rozmieszczenia punktów: a) równomierne, b) Czebyszewa, c) Legendre’a
W przypadku rozmieszczeń punktów w miejscach pierwiastków wielomianów
Czebyszewa lub Legendre’a są one zagęszczone przy krawędziach obszaru i rzadziej, ale
równomiernie rozłożone w jego środku. Przy czym w przypadku wielomianów Czebyszewa
skrajne punkty są bliżej krawędzi brzegu aniżeli w przypadku wielomianów Legendre’a
(rys.1b,c), dlatego też zdecydowano się na przetestowanie obu wariantów rozmieszczeń.
Ostatnim krokiem związanym z tym etapem algorytmu jest automatyczne odwzorowanie
wybranego rozmieszczenia punktów, wygenerowanego dla obszaru kwadratowego 1 1 , na
dowolnie zmodyfikowany kształt obszaru (rys. 2).
PORÓWNANIE METOD APROKSYMACJI POCHODNYCH ROZWIĄZAŃ OTRZYMYWANYCH … 33
Rys.2. Odwzorowanie rozmieszczenia punktów na dowolnie zmodyfikowany obszar
4. ANALIZA REZULTATÓW
Wiarygodność i dokładność zaproponowanej aproksymacji pochodnych została pokazana
na przykładach z zakresu teorii sprężystości. Obliczano naprężenia na brzegu i w obszarze.
Wymagało to znajomości odkształceń, które są pochodnymi cząstkowymi przemieszczeń. W
tym celu wykorzystywane są równania konstytutywne [2]
2Gv
2Gv
 x  2G x 
( x   y   z ),  y  2G y 
( x   y   z ),  y  2G xy , (6)
1  2v
1  2v
oraz geometryczne [4] opisujące stan izotropowego, jednorodnego ciała liniowo-sprężystego
u
u
u
u
v
 x  x ,  y  y ,  xy  0.5( x  y ), PSO :  z  0, PSN :  z 
( x   y ),
(7)
x
y
y
x
1 v
gdzie G to moduł Kirchhoffa, zaś  to współczynnik Poissona. Uzyskane za pomocą
zaprezentowanej techniki naprężenia porównano z rozwiązaniami analitycznymi.
W przykładzie pierwszym rozważono kwadratową tarczę 2x 2 obciążoną siłą zginającą
przyłożoną wzdłuż jednego z boków (rys.3a). Zagadnienie rozwiązano w PSO, zaś użyte do
obliczeń stałe materiałowe to E  1 oraz współczynnik Poissona   0.3 .
a)
b)
Rys.3. Rozważane geometrie: a) kwadratowa tarcza, b) obszar nieregularny
Rozwiązania analityczne [3] przedstawione są za pomocą następujących wzorów
u x  0.195 x 2  0.455( y  1) 2 , u y  0.91x( y  1),  x  0,  y  x .
(8)
Na podstawie dostępnych rozwiązań dokładnych (8) wyznaczono wartości błędów
względnych dla naprężeń  y na brzegu (w 40 punktach, po 10 na każdym boku) i w obszarze
w wybranym przekroju poziomym  1  x  1 oraz y  0.7 . Do otrzymania wyników
aproksymacji pochodnych uwzględniano 16 punktów z obszaru oraz brzegu (wariant 2) i
wszystkie sposoby ich rozmieszczenia. Rezultaty analizy dla naprężeń w obszarze
zaprezentowano na rys.4. W przypadku naprężeń na brzegu średni błąd względny wyniósł
0.039% (dla rozmieszczenia równomiernego).
34
A. BOŁTUĆ, E. ZIENIUK
Jak wynika z rys.4 najbardziej efektywnym jest równomierne rozmieszczanie punktów do
interpolacji rozwiązań, gdyż błąd, jakim są obarczone naprężenia, jest minimalny dla różnej
liczby tych punktów. W przypadku rozmieszczeń charakteryzujących się zagęszczeniem
punktów przy brzegach błąd rośnie wraz ze wzrostem liczby punktów przyjętych do
interpolacji. Bardzo mały jest jedynie dla 16 punktów, zaś przy większej ich liczbie rośnie
diametralnie, szczególnie w przypadku rozmieszczenia w miejscach pierwiastków
wielomianów Czebyszewa. Wynika to z faktu, iż skrajne punkty dobrane do interpolacji
znajdują się w bardzo bliskiej odległości od brzegu (rys.1b). Ma to wpływ na większy błąd
jakim są obarczone rozwiązania uzyskane w tych punktach, co przekłada się na błąd
aproksymacji pochodnych. W przypadku rozmieszczenia w miejscach pierwiastków
wielomianów Legendre’a rozwiązania są nieco lepsze, jednak również mamy do czynienia ze
wzrostem błędu wraz ze wzrostem liczby punktów przyjętych do interpolacji rozwiązań.
Rys.4. Średnie błędy względne dla naprężeń  y w rozpatrywanym przekroju
Podsumowując, technika z doborem punktów na brzegu i w obszarze do interpolacji
rozwiązań (zastosowanych następnie do aproksymacji pochodnych) dała zadowalające wyniki
(wartości naprężeń) dla wszystkich wariantów rozmieszczenia punktów przy małej ich
liczbie. W przypadku stosowania większej liczby punktów najlepszy okazał się wariant
rozmieszczania równomiernego.
W przykładzie drugim rozważono obszar nieregularny pokazany na rys.3b. Zadanie
rozwiązano w PSO, biorąc pod uwagę wartości stałych materiałowych, takie jak w
przykładzie pierwszym. Warunki brzegowe zadano na podstawie bardziej złożonych niż
poprzednio rozwiązań analitycznych dla pola przemieszczeń
u x  6 xy 2  2 y 3 , u y  6 x 2 y  2 x 3 .
(9)
Na ich podstawie wyznaczono pole naprężeń wykorzystując wzory (6,7)
 x  24Gxy ,  y  24Gxy,  xy  12G ( x 2  y 2 ) .
(10)
W przykładzie przebadano wszystkie warianty dobierania punktów do interpolacji
rozwiązań oraz ich rozmieszczenia. Pierwszy etap dotyczył analizy naprężeń  x w
dziewięciu punktach przekroju 0.5  x  4.5 oraz 3  y  5 , zaś wyniki tej analizy dla dwóch
wariantów dobierania punktów do interpolacji przedstawiono na rys. 5.
Zaprezentowane na rys. 5 rezultaty potwierdziły wnioski wyciągnięte w poprzednim
przykładzie. Ponownie najbardziej uniwersalnym wariantem jest równomierne
rozmieszczenie punktów do interpolacji rozwiązań, zarówno w samym obszarze, jak i w
obszarze i na brzegu. W obu przypadkach średni błąd względny dla naprężeń wyniósł
praktycznie 0% (na takim też poziomie pozostaje przy zwiększającej się liczbie punktów do
PORÓWNANIE METOD APROKSYMACJI POCHODNYCH ROZWIĄZAŃ OTRZYMYWANYCH … 35
interpolacji). Przy niewielkiej liczbie punktów do interpolacji ( n  16, 25,36 ) dużą
dokładnością charakteryzują się wszystkie warianty rozmieszczenia, jednak im więcej tych
punktów tym bardziej gwałtownie rośnie błąd. Błąd, jakim obciążone są rozwiązania
uzyskane z wykorzystaniem tzw. rozmieszczenia w miejscach zerowych wielomianu
Czebyszewa, jest wyższy niż dla wielomianu Legendre’a przy tej samej liczbie punktów.
Rozmieszczenia punktów zagęszczone przy brzegach dają również nieco większy błąd, przy
tej samej liczbie punktów, gdy rezultaty aproksymuje się, korzystając z wariantu 1 doboru
punktów (np. dla n  49 rozmieszczenie Legendre’a dla wariantu 2 generuje błąd 0.012%,
zaś dla wariantu 1 błąd 2.5%).
a)
b)
Rys.5. Średnie błędy względne  x dla wariantów doboru punktów: a) z brzegu i obszaru
(wariant 2), b) tylko z obszaru (wariant 1).
W kolejnym etapie aproksymowano naprężenia na brzegu. Przetestowano trzy wymienione
warianty doboru punktów do interpolacji rozwiązań, gdzie brano pod uwagę 16 równomiernie
rozmieszczonych punktów. Wyliczono średni błąd względny dla naprężeń  x uwzględniając
rozwiązania z 36 punktów na brzegu. I tak przy wariancie dobierania punktów z obszaru i
brzegu uzyskano błąd  x  0.013% . Tę samą procedurę zastosowano, biorąc pod uwagę
tylko rozwiązania z obszaru, gdzie naprężenia na brzegu wyznaczono na zasadzie
ekstrapolacji. Ponownie średni błąd względny dla tych rozwiązań jest bliski zera:
 x  0.062% . Niepowodzeniem (w tym przykładzie) zakończyła się próba zastosowania
wariantu dobierania rozwiązań do aproksymacji jedynie z brzegu, gdzie otrzymany błąd
przekroczył 20% .
36
A. BOŁTUĆ, E. ZIENIUK
5. WNIOSKI
Zaprezentowane przykłady potwierdziły efektywność zaproponowanej techniki
aproksymacji pochodnych dowolnego rzędu. Technika bazuje na interpolacji znanych
rozwiązań w wybranych punktach i zróżniczkowaniu wielomianów w szeregach
interpolacyjnych. Przetestowano różne warianty dobierania punktów oraz ich rozmieszczenia.
Warianty z rozmieszczeniem na brzegu i w obszarze oraz tylko w obszarze okazały się
najbardziej uniwersalne, zaś rozmieszczenie jedynie na brzegu dało poprawne wyniki tylko w
niektórych przykładach. Wersja z rozmieszczeniem równomiernym dała dokładne i stabilne
wyniki, zaś koncepcje umieszczania ich w miejscach pierwiastków wielomianów Czebyszewa
czy Legendre’a okazały się skuteczne tylko dla niewielkiej liczby punktów. Można
stwierdzić, że zaproponowana technika pozwala na efektywne rozwiązywanie zagadnień, w
których wymagana jest znajomość pochodnych cząstkowych rozwiązań. Dlatego też
zachęcające jest jej zastosowanie do rozwiązywania zagadnień plastycznych, gdzie napotkano
problem konieczności obliczania silnie osobliwych całek obecnych w tożsamości całkowej
dla naprężeń oraz zagadnień identyfikacji bądź optymalizacji.
LITERATURA
1. Abramowitz M., Stegun I. A.: Handbook of mathematical functions with formulas,
graphs, and mathematical tables. New York: Dover, 1965.
2. Ameen M.: Computational elasticity. Harrow: Alpha Science International Ltd., 2005.
3. Panzeca T., Fujita Yashima H., Salerno M.: Direct stiffness matrices of BEs in the
Galerkin BEM formulation. “European Journal of Mechanics and Solids” 2001, 20, p.
277-298.
4. Zieniuk E.: Potential problems with polygonal boundaries by a BEM with parametric
linear functions. “Engineering Analysis with Boundary Elements” 2001, 25, p. 185-190.
5. Zieniuk E., Bołtuć A.: Bézier curves in the modeling of boundary geometry for 2D
boundary problems defined by Helmholtz equation. “Journal of Computational
Acoustics” 2006, 14/3, p. 353-367.
6. Zieniuk E., Bołtuć A.: Non-element method of solving 2D boundary problems defined on
polygonal domains modeled by Navier equation. “International Journal of Solid and
Structures” 2006, 43, p. 7939-7958.
THE COMPARISON OF METHODS FOR THE APPROXIMATION
OF DERIVATIVE OF SOLUTIONS OBTAINED USING PIES METHOD
IN BOUNDARY PROBLEMS
Summary. The paper presents a technique for the approximation of the
derivatives of boundary problems solutions obtained by PIES. The main aim was
to avoid calculating these derivatives analytically (which is quite complicated,
even impossible) or numerically at specific points (because it is time consuming
and inefficient). The effectiveness of the proposed technique consists of
computing the derivatives in a continuous way and at any points of the boundary
and area by developed approximating series. The reliability and accuracy of the
strategy has been tested on examples with analytical solutions.