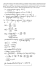rozwiązania

Metody probabilistyczne i statystyka
Kolokwium I, 16 listopada 2010 r.
Zadanie 1. Jakie jest prawdopodobieństwo, że w losowaniu Lotto (6 kul z 49, bez powtórzeń) nie
wypadną żadne dwie kolejne liczby?
Rozwiązanie. Niech Ω oznacza przestrzeń wszystkich zdarzeń elementarnych (możliwych wyborów
6 kul z 49). Oczywiście |Ω| = 49
6 . Wystarczy teraz zauważyć, że wylosowanie 6 kul jest równoważne
z określeniem ile dokładnie kul występuje pomiędzy kolejnymi dwiema wybranymi kulami. Zatem do
każdej z 5 luk pomiędzy wybranymi kulami należy wrzucić przynajmniej po jednej kuli, a pozostałe
(49 - 6 - 5 = 38) kule umieścić w dowolny sposób w 7 lukach (5 pomiędzy wybranymi kulami, jedna
przed, jedna za). Zatem jeżeli zbiór zdarzeń sprzyjających oznaczymy przez A, to
!
|A| =
38 + 7 − 1
38
!
=
44
38
!
=
44
.
6
Ostatecznie
|A|
=
P(A) =
|Ω|
44
6
49 .
6
Uwaga. Formalnie, liczba sposobów wybrania 6 kul o żądanej własności jest taka sama jak liczba ciągów
7-elementowych (a0 , a1 , a2 , a3 , a4 , a5 , a6 ), gdzie ai ∈ Z, dla i = 0, . . . , 6, ai ­ 1 dla i = 1, . . . , 5, oraz
P6
i=0 ai = 43. Przykładowo, ciąg (0, 2, 2, 1, 10, 10, 18) jest równoważny wyborowi kul o numerach 1, 4,
7, 9, 20, 31.
Zadanie 2. Z przedziału [0, 1] wylosowano dwie liczby rzeczywiste a i b. Jakie jest prawdopodobieństwo, że równanie
x2 − 2ax + b = 0
ma dwa różne pierwiastki rzeczywiste, których iloczyn jest mniejszy od 41 ?
Rozwiązanie. Równanie to ma dwa pierwiastki rzeczywiste wtedy i tylko wtedy, gdy
∆ = 4a2 − 4b > 0,
czyli dla a2 > b. Ponadto iloczyn pierwiastków tego równania jest równy b (co wynika z prostych
rachunków lub wzorów Viete’a). Zatem dla Ω = [0, 1] × [0, 1] zbiorem zdarzeń sprzyjających jest
A = {(a, b) ∈ Ω : b < a2 , b < 1/4},
czyli
b
1
Ω
(
1 1
,
2 4
)
A
O
1
1
a
2
Stąd
|A|
P(A) =
=
|X|
Z 1/2
0
1/2
1
x3 x2 dx + =
8
3
+
0
1
1
1
1
=
+ = .
8
24 8
6
Zadanie 3. Niech A, B ⊂ Ω będą pewnymi zdarzeniami, przy czym 0 < P(B) < 1. Pokazać, że
P(A) − P(B c )
P(A)
¬ P(A|B) ¬
.
P(B)
1 − P(B c )
Rozwiązanie. Ponieważ A ∩ B ⊂ A, to P(A ∩ B) ¬ P(A). Stąd mamy
P(A|B) =
P(A)
P(A)
P(A ∩ B)
¬
=
.
P(B)
P(B)
1 − P(B c )
Z drugiej strony,
P(A|B) =
P(A ∩ B)
P(A \ B c )
P(A \ (B c ∩ A))
P(A) − P(B c ∩ A)
P(A) − P(B c )
=
­
=
­
.
P(B)
P(B)
P(B)
P(B)
P(B)
Zadanie 4. W urnie znajdują się 3 kule, z których każda jest biała lub czarna (z jednakowym prawdopodobieństwem). Wylosowano kolejno z urny 4 kule ze zwracaniem, w kolorach białym, czarnym,
czarnym, czarnym (dokładnie w tym porządku). Jakie jest prawdopodobieństwo, że w urnie znajdowały
się dwie kule czarne i jedna biała?
Rozwiązanie. Oznaczmy zdarzenia
AA3,0 A2,1 A1,2 A0,3 -
wylosowano kolejno
w urnie znajdowały
w urnie znajdowały
w urnie znajdowała
w urnie znajdowały
kulę białą, czarną, czarną, czarną,
się 3 kule białe,
się 2 kule białe i jedna czarna,
się 1 kula biała i dwie czarne,
się 3 kule czarne.
Chcemy znaleźć prawdopodobieństwo P(A1,2 |A). Ze wzoru Bayesa mamy
P(A1,2 |A) =
P(A|A1,2 )P(A1,2 )
.
P(A|A3,0 )P(A3,0 ) + P(A|A2,1 )P(A2,1 ) + P(A|A1,2 )P(A1,2 ) + P(A|A0,3 )P(A0,3 )
Ponieważ P(A|A3,0 ) = P(A|A0,3 ) = 0, to
P(A1,2 |A) =
Teraz
oraz
P(A|A1,2 )P(A1,2 )
.
P(A|A1,2 )P(A1,2 ) + P(A|A2,1 )P(A2,1 )
(1)
3
P(A1,2 ) = P(A2,1 ) = ,
8
1 2 2 2
8
· · · = ,
3 3 3 3
81
2 1 1 1
2
P(A|A2,1 ) = · · · = .
3 3 3 3
81
Wstawiając uzyskane wartości do wzoru (1), otrzymujemy
P(A|A1,2 ) =
P(A1,2 |A) =
8
81
·
8
81 ·
3
8 +
3
8
2
81
·
3
8
=
24
4
= .
30
5
Zadanie 5. W urnie X znajdują się 2 kule białe i 8 czarnych, natomiast w urnie Y , 3 kule białe i 7
czarnych. Z zewnątrz urny są dla nas nierozróżnialne. Będziemy losować dwa razy kolejno po jednej
kuli z wybranej przez nas urny (bez zwracania), przy czym po wyjęciu pierwszej kuli możemy zmienić
urnę. Jak powinniśmy losować, aby prawdopodobieństwo wyjęcia dwóch kul białych było największe?
3
Rozwiązanie. W rozwiązaniu należy zdecydować, czy po wyjęciu pierwszej kuli białej bardziej opłaca
się losować następną kulę z tej samej urny, czy z drugiej.
Niech
A - wylosowaliśmy 2 kule białe,
AX - losujemy pierwszą kulę z urny X,
AY - losujemy pierwszą kulę z urny Y .
Niech strategia 1. polega na losowaniu drugiej kuli z tej samej urny. Wtedy
2 1 1
3 2 1
2
P(A) = P(A|AX )P(AX ) + P(A|AY )P(AY ) =
· · +
· · = .
10 9 2 10 9 2
45
Analogicznie, w przypadku strategii 2. (zmiana urny po pierwszym losowaniu) mamy
2 3 1
3 2 1
3
P(A) = P(A|AX )P(AX ) + P(A|AY )P(AY ) =
·
· +
·
· = .
10 10 2 10 10 2
50
2
3
Ostatecznie 45 < 50 , więc lepiej jest zmienić urnę do drugiego losowania.
(ag)