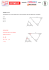Algorytmy stochastyczne — laboratorium 03

Algorytmy stochastyczne — laboratorium 03
Jarosław Piersa
10 marca 2014
1
Projekty
1.1
Problem plecakowy (1p)
Oznaczenia:
• dany zbiór przedmiotów x1 , .., xN ,
• każdy przedmiot ma określoną wagę w(xi ) i wartość v(xi ),
• plecak ma ograniczoną pojemność maxW ,
• przedmiot może być zapakowany tylko jeden raz, ale może się znaleźć w dwóch różnych egzemplarzach na liście.
Cel: wybrać podzbiór przedmiotów o maksymalnej wartości i mieszczący się w limicie wagowym maxW .
Kodowanie:
• osobnik ō = [o1 , .., oN ], oi = 1 ⇐⇒ zabieramy xi do plecaka,
• krzyżowanie i mutacje: klasyczne...
• (plus naprawa niepoprawnego osobnika) w wypadku przekroczenia wagi usuwamy losowe przedmioty aż do zmieszczenia
się w limicie.
P
˙
• (lub kara) w wypadku przekroczenia wagi zmniejszamy wartość osobnika o c(∆W
)2 , gdzie ∆W = max(0, ( i wi oi ) −
maxW ) = przekroczenie wagi.
1.2
Problem komiwojażera (2p)
Dany jest graf G = (V, E), oraz wagi krawędzi w (w wersji prostej: w(e) = długość krawędzi).
Oznaczenia:
• v ∈ V — wierzchołek w grafie,
• e ∈ E — krawędź w grafie,
• w(e) ∈ R+ — waga / długość krawędzi / odległość między miastami,
• jeżeli (vi , vj ) ∈
/ E to można przyjąć w((vi , vj )) = określone, ale duże np w((vi , vj )) = maxk
wagach,
Cel: znaleźć cykl w grafie o minimalnej długości
1.2.1
Reprezentacja ścieżkowa osobnika
• ō = [o1 , o2 , o3 , o4 ], gdzie oi = 1..N — numer miasta,
• odwiedzamy miast vi w i-tym kroku cyklu,
• np. ō = [3, 2, 4, 1] odpowiada cyklowi 3 → 2 → 4 → 1 → 3,
• UWAGA! ten sam cykl odpowiada osobnikom [2, 4, 1, 3], [4, 1, 3, 2], ...,
Mutacje:
• transpozycja (zamieniamy miejscami dwa losowe miasta),
• odwrócenie podciągu (odwracamy losowo wybrany fragment cyklu).
Krzyżowanie PMX (ang. partialy mapped crossover ):
1
P
l
w((vk , vl )) po określonych
• wybieramy pod-odcinek: p̄ = [p1 ...p2 |p3 ...p4 |p5 ..p6 ], q̄ = [q1 ...q2 |q3 ...q4 |q5 ..q6 ]
• potomkowi ustawiamy pod-odcinek z q: r := [...|q3 , q4 |...]
• uzupełniamy głowę i ogon o miasta z p̄ (zachłannie kopiujemy na wolne miejsca tam gdzie jest to możliwe): r :=
[p1 ...|q3 , q4 |p5 ...] (tak aby nie zniszczyć cyklu!)
• uzupełniamy pozostałe miasta z p aby powstał poprawny cykl, r = [p1 r2 |q3 , q4 |p5 r6 ],
• krzyżowanie nie wyprowadza poza zbiór poprawnych cykli!
Analogicznie można utworzyć drugiego potomka r2 .
Kolejne kroki PMX:
• p = [5, 7, 8|1, 4, 2|6, 3]
• q = [4, 3, 1|2, 6, 5|8, 7]
• r = [., ., ., |2, 6, 5|., .] (kopiujemy z q)
• r = [., 7, 8|2, 6, 5|., 3] (kopiujemy z p)
• r = [1, 7, 8|2, 6, 5|4, 3](uzupełniamy nieodwiedzonymi z p)
Krzyżowanie OX (order-based crossover ):
• wybieramy pod-odcinek: p̄ = [p1 ...p2 |p3 ...p4 |p5 ..p6 ], q̄ = [q1 ...q2 |q3 ...q4 |q5 ..q6 ]
• wstawiamy potomkowi odcinek z q: r = [...|q3 , ...q4 |...]
• uzupełniamy głowę i ogon o miasta z p̄ ale zachowując kolejność odwiedzeń: r = [p1 ...|q3 , ...q4 |p5 ...], zaczynamy
od pozycji p5 (następna po wstawionym bloku z q)
Podobnie można utworzyć drugiego potomka zamieniając role p i q.
Kolejne kroki OX:
• p = [5, 3, 2|1, 4, 8|6, 7]
• q = [4, 3, 1|2, 6, 5|8, 7]
• r = [., ., ., |2, 6, 5|., .] (kopiujemy z q)
• r = [., ., ., |2, 6, 5|7, .] (kopiujemy z p)
• r = [., ., ., |2, 6, 5|7, 3]
• r = [1, ., ., |2, 6, 5|7, 3]
• r = [1, 4, ., |2, 6, 5|7, 3]
• r = [1, 4, 8, |2, 6, 5|7, 3]
Krzyżowanie CX (cycle-based crossover ):
• Pomysł: każde wystąpienie musi pochodzić od któregoś z rodziców
• pierwszą wolną pozycje bierzemy od jednego z rodziców (np pi ), na początku i = 1
• jeżeli pi 6= qi , to zablokowaliśmy możliwość wyboru qi ,
• musimy zatem wziąć to miasto również z rodzica p z pozycji j, tj pj
• jeżeli zamknęliśmy cykl i potomek jest zakończony to zakończ.
• jeżeli zamknęliśmy cykl, ale osobnik nie jest zakończony do Pkt 2, ale wybierz wolną pozycję z drugiego rodzica (jak
był p, to teraz q).
• jeżeli jeszcze nie zamknęliśmy cyklu to i := j i punkt 3.
Kolejne kroki CX:
• p = [1, 3, 2, 5, 4, 8, 6, 7]
• q = [2, 3, 1, 4, 6, 5, 8, 7]
2
• r = [1, ...] (kopiujemy z p)
• r = [1, ., 2, ...] (koniec cyklu)
• r = [1, 3, 2, ...] (następny cykl, jeden element)
• r = [1, 3, 2, 4...] (kopiujemy z q)
• r = [1, 3, 2, 4, ., 5, ...]
• r = [1, 3, 2, 4, ., 5, 8, .]
• r = [1, 3, 2, 4, 6, 5, 8, .] (koniec cyklu)
• r = [1, 3, 2, 4, 6, 5, 8, 7]
1.2.2
Reprezentacja macierzowa osobnika
• reprezentacja: macierz kwadratowa A wymiaru N × N , N = liczba miast,
• jeżeli miasto i leży na ścieżce przed miastem j to aij = 1 / wersja tablicowa A[i, j] = 1,
• ai,i = 0 zawsze,
• relacja jest przechodnia zatem jeżeli aij = 1 i ajk = 1 to również aik = 1,
• w tablicy jest dokładnie N (N − 1)/2jedynek
Mutacja
• zamieniamy parę miast miejscami
• aij := 1 − aij ,
• aji := 1 − aji .
Krzyżowania:
• Rodzice P oraz Q → potomek R,
• R = min(P, Q) (po współrzędnych),
• resztę dopełniamy losowo,
• jeżeli rij = rji = 0, to losowy z nich ustawiamy na 1,
• krzyżowanie może prowadzić poza zbiór poprawnych osobników.
Krzyżowanie 1 — przekrój
• Rodzice P oraz Q → potomek R
• R = min(P, Q) (po współrzędnych)
• resztę dopełniamy losowo
• jeżeli rij = rji = 0, to losowy z nich ustawiamy na 1
Krzyżowanie 2 — Blokowe
• Rodzice P oraz Q → potomek R
• Potomek
R=
PI
1 − randtr
rand
QII
dwa bloki diagonalne z rodziców, pozostałe uzupełniamy
• może wygenerować potomka z poza zbioru (tzn. rij = rjk = 1, ale rik = 0)
3
1.3
Wyszukiwanie ścieżek na R2 (2p)
• dana para punktów na płaszczyźnie: S = (xs , ys ), D = (xd , yd )
• dane przeszkody na płaszczyźnie: np. zbiór kół: Ki = ((xi , yi ), ri ), wielokątów wypukłych (np trójkątów, reprezentacja
wektorowa) lub piskeli (rastrowa).
a3
a2
D
S
a1
a4
Cel
• znaleźć ścieżkę z S do D
• o minimalnej długości
• bez ostrych zakrętów
• omijającą przeszkody (z pewnym marginesem bezpieczeństwa R)
Reprezentacja osobnika
• lista punktów na R2 ,
• O = [a0 = S, a1 , a2 ..., ak = D], długość listy może być zmienna,
• interpretacja: ścieżka S = ao → a1 → a2 → · · · → ak = D,
• długość ścieżki:
L(O) =
k
X
|ai−1 , ai |,
i=1
gdzie |−, −| oznacza zwykłą odległość
• margines bezpieczeństwa: niech
0 jeżeli w promieniu R od punktu a nie ma żadnej przeszkody
M (a) =
R − odległość do najbliższej przeszkody
oraz dla całej ścieżki
M (O) :=
k−1
X
M (ai )
i=1
• gładkość(xi ) = π− kąt pomiędzy sąsiednimi krawędziami
α
ai+1
ai
ai−1
• gładkość(O) =
Pk−1
i=1
gładkość(xi )
Krzyżowania:
• (dwoje rodziców P,Q → dwoje potomków) złączenie początku ścieżki P i końca ścieżki Q, drugi potomek — symetrycznie, punkt łączenia — losowy, P i Q mogą mieć różne długości!
4
Mutacje:
• przesunięcie punktu pośredniego o wektor z rozkładu normalnego x = x + N ([0, 0], I2 ),
• przesunięcie punktu pośredniego do losowej pozycji z dopuszczalnego zakresu,
• dodanie / usunięcie wierzchołka pośredniego (uwaga! dodawanie pomiędzy losową parę może powodować niestabilności
numeryczne, należy dodawać jeżeli segment drogi jest za długi, a usuwać gdy jest za krótki).
5