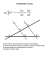Zadania i rozwiązania etap 2

X Wrocławski Konkurs Matematyczny dla uczniów klas I-III gimnazjów
rok szkolny 2014/2015
Etap II
Zadanie 1
Uczniowie otrzymali z pracy klasowej oceny 2, 3, 4 i 5. Ocen 2, 3 i 5 było tyle samo,
a czwórek było więcej niż wszystkich pozostałych ocen. Więcej niż trójkę otrzymało mniej niż
10 uczniów. Ilu uczniów otrzymało trójkę, jeśli klasówkę pisało nie mniej niż 12 uczniów.
Zadanie 2
W trójkącie ABC bok AB ma długość 3 cm oraz bok AC ma długość 2 cm. Gdy na boku AB
zaznaczono punkt D w odległości 2 cm od wierzchołka A, to okazało się, że miara kąta
∡ CDA jest dwa razy większa niż miara kąta ∡ CBA. Oblicz długość boku BC.
Zadanie 3
Maszyna A wykonuje daną pracę w czasie 11 razy dłuższym niż maszyny B i C pracujące
jednocześnie. Maszyna B wykonuje tę pracę w czasie 5 razy dłuższym niż maszyny A i C
pracujące jednocześnie. Ile razy szybciej wykona tę pracę maszyna C niż jednocześnie
pracujące maszyny A i B?
Zadanie 4
Wielokąt foremny o n bokach nazywamy krótko n-kątem foremnym. Funkcja f każdej liczbie
naturalnej n większej od 2 przyporządkowuje liczbę wyrażającą pole pierścienia kołowego
ograniczonego okręgiem opisanym na n-kącie foremnym o boku długości 2, a okręgiem
wpisanym w ten n-kąt. Uzasadnij, że funkcja f dla wszystkich argumentów przyjmuje tę samą
wartość.
Zadanie 5.
Wyznacz wszystkie pary (p,q) liczb pierwszych spełniające równanie p2 =12q2+1.
Zadanie 6
Dany jest kąt o mierze 60° oraz punkt P leżący wewnątrz tego kąta. Odległości punktu P od
ramion tego kąta są równe a i b. Udowodnij, że odległość punktu P od wierzchołka kąta jest
równa
2
3
a2
ab b 2 .
Przykładowe rozwiązania
Zadanie 1
Uczniowie otrzymali z pracy klasowej oceny 2, 3, 4 i 5. Ocen 2, 3 i 5 było tyle samo,
a czwórek było więcej niż wszystkich pozostałych ocen. Więcej niż trójkę otrzymało mniej niż
10 uczniów. Ilu uczniów otrzymało trójkę, jeśli klasówkę pisało nie mniej niż 12 uczniów.
Rozwiązanie:
x – liczba trójek (dwójek, piątek),
y – liczba czwórek.
Na podstawie warunków zadania otrzymujemy:
y
3x
x
y 10
3x
y 12
Liczba x > 1, bo w przeciwnym wypadku y < 9 i y
9 wykluczają się
Z pierwszego i trzeciego równania wynika, że y > 3x ≥ 12 – y, zatem y > 6.
Warunki x >1, y > 6 i x + y < 10 spełniają liczby x = 2 i y = 7
Odpowiedź: Dwóch uczniów otrzymało trójkę.
Zadanie 2
W trójkącie ABC bok AB ma długość 3 cm oraz bok AC ma długość 2 cm. Gdy na boku AB
zaznaczono punkt D w odległości 2 cm od wierzchołka A, to okazało się, że miara kąta
∡ CDA jest dwa razy większa niż miara kąta ∡ CBA. Oblicz długość boku BC.
Rozwiązanie:
Oznaczmy przez α miarę kąta CBA. Miara kąta CDA jest równa 2α. Kąt BDA jako przyległy
do kąta CDA ma miarę 180°−2α i stąd miara kąta DCB jest równa: 180°−(α + 180° − 2α) = α
|AB| = 3 oraz |AD| = 2 a stąd długość odcinka BD jest równa 1 gdyż:
|DB| = |AB| − |AD| = 3 – 2 = 1.
Trójkąt BCD jest równoramienny, więc długość odcinka CD też jest równa 1.
Niech CE będzie wysokością trójkąta ABC poprowadzoną z wierzchołka.
Oznaczmy: h = |CE| oraz x = |DE|. Wtedy |AE| = 2 − x.
Trójkąty AEC i DEC są prostokątne więc z twierdzenia Pitagorasa wynika, że:
h2 = 22 − (2 − x)2 oraz h2 = 12 − x2. czyli
22 − (2 − x)2=12 − x2
x=
1
4
h2 = 12 – x2
h
15
4
Stosując twierdzenie Pitagorasa do trójkąta EBC obliczamy długość boku BC:
|BC|2 = (x + 1)2 + h2
10
2
|BC| =
Odpowiedź: Długość boku BC jest równa
10
.
2
Zadanie 3
Maszyna A wykonuje daną pracę w czasie 11 razy dłuższym niż maszyny B i C pracujące
jednocześnie. Maszyna B wykonuje tę pracę w czasie 5 razy dłuższym niż maszyny A i C
pracujące jednocześnie. Ile razy szybciej wykona tę pracę maszyna C niż jednocześnie
pracujące maszyny A i B?
Rozwiązanie:
Oznaczmy odpowiednio przez WA, WB, WC wydajności maszyn A, B i C.
Wówczas
WA
WB
WA
WB
1
(WB WC )
11
1
(W A WC )
5
1
WC
9
2
WC
9
WA WB
1
WC
3
Odpowiedź: Maszyna C wykona pracę w czasie 3 razy krótszym niż maszyny A i B
pracujące jednocześnie.
Zadanie 4
Wielokąt foremny o n bokach nazywamy krótko n-kątem foremnym. Funkcja f każdej liczbie
naturalnej n większej od 2 przyporządkowuje liczbę wyrażającą pole pierścienia kołowego
ograniczonego okręgiem opisanym na n-kącie foremnym o boku długości 2, a okręgiem
wpisanym w ten n-kąt. Uzasadnij, że funkcja f dla wszystkich argumentów przyjmuje tę samą
wartość.
Rozwiązanie:
n - liczba naturalna większa od 2. Rozważmy n-kąt
foremny o boku długości 2.
A, B - dowolne dwa sąsiednie wierzchołki tego n-kąta.
O - wspólny środek okręgu opisanego na n-kącie
i okręgu wpisanego w ten n-kąt.
R - promień okręgu opisanego na n-kącie.
r - promień okręgu wpisanego w ten n-kąt.
Wówczas trójkąt o wierzchołkach AOB, jest trójkątem równoramiennym, w którym:
|OA| = |OB| = R
|AB| = 2.
Promień r okręgu wpisanego w n-kąt foremny jest prostopadły do boku AB w punkcie
styczności, więc promień ten stanowi wysokość trójkąta równoramiennego AOB.
Niech M będzie środkiem boku AB. Wtedy |OM| = r.
Trójkąt OMA jest trójkątem prostokątnym, w którym przyprostokątne mają długości |OM| = r,
|AM| = 1 oraz przeciwprostokątna ma długość |OA| = R.
Z twierdzenia Pitagorasa dla trójkąta OMA wynika, że R2 − r2 = 1.
Wobec tego pole pierścienia ograniczonego okręgami opisanym i wpisanym w ten n-kąt jest
równe:
f(n) = πR2 − πr2 = π(R2 − r2)
f(n) = π(R2 − r2)
Ponieważ R2 − r2 = 1, otrzymujemy:
f(n) = π ∙ 1
f(n) = π
Z powyższych obliczeń wynika, że pole pierścienia nie zależy od liczby n i jest równe π.
To oznacza, że funkcja f dla każdego argumentu n przyjmuje tę samą wartość π.
Zadanie 5.
Wyznacz wszystkie pary (p, q) liczb pierwszych spełniające równanie p2 =12q2+1.
Rozwiązanie
Liczba 12q2+1 jest liczbą nieparzystą, więc liczba p musi być liczbą nieparzystą. Przyjmijmy
p = 2n + 1, gdzie n jest dodatnią liczba całkowitą. Wtedy p2 = 4n2 + 4n + 1 = 12q2 + 1,
4n2 + 4n = 12q2
skąd
n2 + n = 3q2
n(n + 1) = 3q2.
Lewa strona ostatniej równości, jako iloczyn dwóch kolejnych liczb całkowitych, jest liczbą
parzystą, stad prawa strona tej równości też jest liczbą parzystą. Zachodzi to tylko dla liczby
pierwszej q = 2. Dane w zadaniu równanie przyjmuje więc postać
p2 = 12 ∙ 22 + 1 = 49, czyli p = 7.
Odpowiedź: Równanie spełnia tylko jedna para liczb pierwszych: (p, q) = (7, 2).
Zadanie 6
Dany jest kąt o mierze 60° oraz punkt P leżący wewnątrz tego kąta. Odległości punktu P od
ramion tego kąta są równe a i b. Udowodnij, że odległość punktu P od wierzchołka kąta jest
równa
2
3
a2
ab b 2 .
Rozwiązanie
Niech C będzie punktem przecięcia prostej BP
i ramienia AS kąta.
Trójkąt
SBC
jest
„połową”
trójkąta
równobocznego. Trójkąt APC także jest
„połową” trójkąta równobocznego,
A stąd PC = 2a. Zatem BC = 2a + b
BS
BC
3
2a b
3
Z twierdzenia Pitagorasa dla trójkąta BPS otrzymujmy
x
BS
2
b
2
To kończy dowód.
2a b 2
(
)
3
b
2
4a 2
4b b 2
3
3b 2
3
2
a2
3
ab b 2