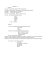Podstawy i zastosowania rachunku tensorowego

Transkrypt

PRACE IPPT · IFTR REPORTS
1/2007
Janina Ostrowska - Maciejewska
PODSTAWY I ZASTOSOWANIA RACHUNKU
TENSOROWEGO
(Wykład na Studiach Doktoranckich w IPPT PAN)
INSTYTUT PODSTAWOWYCH PROBLEMÓW TECHNIKI
POLSKIEJ AKADEMII NAUK
WARSZAWA 2007
ISBN 978-83-89687-02-9
ISSN 0208-5658
Redaktor Naczelny:
doc. dr hab. Zbigniew Kotulski
Recenzent:
prof. dr hab. inż. Piotr Perzyna
Praca wpłynęła do Redakcji 30 czerwca 2006 r.
Skład: Zdzisław Nowak
Instytut Podstawowych Problemów Techniki PAN
Nakład: 100 egz. Ark. druk.: 11,6
Oddano do druku w maju 2007 roku
Druk i oprawa: Drukarnia Braci Grodzickich, Piaseczno, ul. Geodetów 47a
Poświęcam pamięci
Marii Duszek – Perzynie i Andrzejowi Königowi
moim Przyjaciołom, z którymi razem zaczynaliśmy zgłębiać tajniki
rachunku tensorowego
!"$#%&'#
)+*,) -/.103254 *6*6*6*7*6*6*7*6*6*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
)+*:9 ;=<?>@.A0CBED<DGFH4I<KJ12L5MNBOM74I<+.103P@QRBS0UTVDXWFLZYBK[@MNLF\<+]3^3<?>`_baD
L5MNcedfNTLCY *6*6*7*6*6*7*6*6*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
)+*ih -jT?k@^lBb[`F6F5QmF5WF5[$0UTnQN<bd+MN_eMoWpBK03F5WqBK0rTLs5[@FrJtM
^3BbLCY?P@[`_?Pus>Bbv
wxzyo{|S}~o{}|#?&'+"?%#
9*,) ;=<SJ125LMNFdb^3P@4$TM
LMRB?fB *6*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
9*:9 ;^3sF5.103^3sF5[@MNF6QmMN[@Mm<|DF*6*6*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
9*ih >`Ds<+^3<|DBb[@MNB.A0l^3P`_e03P@^BKQNd+Fk@^lBbMmL5s[eT?LCY *6*6*7*6*6*6*7*6*6*
9* ;^3sF5.103^3sF5[@MNF6FP@_eQNMN>`F5.3<|DF*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
xG#?%=5|#?}~
'&'!#?5?#
h`*,) ;^3sF5.103^3sF5[@MNF03F5[@.1<+^3<|DF*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
h`*:9 sMRB?fBb[@MNB[B03F5[@.1<+^lBbLCY*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
h`*ih F5[@.1<+^1T>`^3P@d+MmF5d+<^3s52>@PV*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
¡¢}
{|I£\|¤"e£zH="$#?{|"$#?%=&¥{|#?%=5?
K¦
@*,) F5[@.1<+^1T<b^10l<bd+<+[BbQm[@F *6*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
@*:9 ¨P0l<+W<+Â©s5W Tp4@^3sF5.103^3sF5[@M03F5[@.1<+^3<|DtT?LZY *6*6*7*6*6*6*7*6*6*
@*ih ª«^3P@4$T.ATWF03^3MmM¬0lF5[`.3<+^3B*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
@* ;^3s®T_@fBb>`Td+^3P`4.1T?WF0l^1MNM¯*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
§xG#?%=5|O+"+`{E#?/"$°!}x±C'&²%&'? z{|#eK&j=°e³+{|IÉ$&
*,) ·<+s5_@fBb>.34IF_e03^lBbQm[eTn0lF[@.3<b^3aD¸LsDBb^103F5d+<q^1s52>@P *6*6*7*6*6*
*:9 ;^3<SJ1F5_$03<+^1TbºW<?>@PofNT»«F5Q,¼Mm[B½*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
*ih F5[@.1<+^¾.10lBb[ePud+^3Bb[@MmL5s5[`F5d+<S¿rF5[`F5^3dbF0rTLs5[@F6.10CBK[eTnDfBK.3[@Fp*6*6*
* ª«^3P@4$T.ATWF03^3MmM¬0lF5[`.3<+^1aD¸LsDBbÂ0lFd+<q^1s525>`Pj*6*7*6*6*6*7*6*6*
µxÀ
}=%~ICÁ5#z{|#?%5 #
`*,) ÃP@[@_bLrJ1F0lF[@.3<b^3<|DF7Bb^3dbP@WqF[e03P03F5[@.1<+^3<|DFd+<Ä*7*6*6*6*7*6*6*
`*:9 ª«^3P@4$T.ATWF03^3MmM¬ÅP@[@_bLrJ1M
0lF[@.3<b^3<DtT?LCYÆ*6*7*6*6*7*6*6*6*7*6*6*
`*ih ;=<?>@.A0CBED<DGF¥0rDMNF^3>@sF5[@MNBt<t^3F54`^3F5sF5[$0CBbLrJ1M+ÅP@[@_bLUJ1Mb0lF[@.3<+^1<DtT?LCY
MNs<b03^3<+4I<|DtTLCY *6*6*7*6*6*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
(
8
g
+) )
`(
)|g
9b
9bh
9+8

h+h
h+
e §§
+ bg
+
b
µ¶
+¹
8+ g$8
)E$9
eÂ¬(
)E$8
)E+¹
)b)9
µ
Ç+ÈIÉNÊ¥Ë'ÌlÍCÎ|Ï®É
`* -/s5a+^¾Ð?T?QmDF.10l^3BS¿UÑBbdb^lBb[@dbFKÒ:Bn*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
`*: ÃP@[@_bLrJ1F0lF[@.3<b^3<|DF64I<b0lF[@LUJ3BKQN[@FÓ*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
(oÔo{E#%5 #
8*,) ;=<+QNB.1_SBbQNBb^3[@FKº@DF_$0l<+^1<DF6Mx03F5[@.1<+^3<|DFÕ*7*6*6*7*6*6*6*7*6*6*
8*:9 Ö_@fBb>`TnD.34Ia?f^3s25>@[$TLCYz_Bb^[email protected]_eMNLCY×*7*6*6*7*6*6*6*7*6*6*
8*ih -/.34IafR^3s25>@[@F6_e^3sTeD<bQNMN[`MN<|DF *6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
ØxÙnÚ³e%&²+"$~?@%=&#u&+¬ÛÜ~?%&#Ý¥ÚIÞ{|#?%=5S¦
g`*,) 4IF5^3BbLUJ1F^3abß5[@MmL5s5_K<DF6[B4I<+QRBKLZY0lF[@.3<b^3<|DtTLCYà*6*6*6*7*6*6*
g`*:9 ·a+ß5[`MNL5s_b<DBb[@MNF«4Ia+Qx03F5[@.1<+^3<|DtT?LZYuDáP@_@fBb>@BbLCY
_SBK^10lFsUJ3Bbv`.3_eMNLCYâ*6*6*7*6*6*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
g`*ih ·a+ß5[`MNL5s_b<DBb[@MNF«4Ia+Qx03F5[@.1<+^3<|DtT?LZYuDáP@_@fBb>@BbLCY
_e^3s®T?DG<+QNMm[@MN<|DtT?LZYã*6*7*6*6*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
g`* 4IF5^3BbLUJ1FLEBef_b<|DF6[B4I<bQRBbLCY0lF[@.3<+^1<DtT?LCY *6*7*6*6*6*7*6*6*
g`*: DMNF^3>@sF5[@MNBLEB?fR_b<DGF *6*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
¶xzä7"$5"$#®{|"e#?å¤="+
~
&G~
'®+"e%#®Á
¹`*,) æuMNBb^lBL5s5Bb.3Pç*7*6*6*7*6*6*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
¹`*:9 >@QmF5dfR<+]3è«s5>@Bb^3sF5v*7*6*6*7*6*6*6*7*6*6*6*7*6*6*7*6*6*6*7*6*6*
¹`*ih ¨P0l<+W<+Â©s5W TpL5s5Bb.3<+4`^3s5F.10l^1s5F5[@M *6*6*6*7*6*6*7*6*6*6*7*6*6*
¹`* [email protected]^1DBK0l<+^4@^1s5F5.A0l^1s5F5[`MM
P@_@fBb><?>@[@MNF.3MmF5[@MNBé*7*6*6*6*7*6*6*
ê !`{E#?~
ë &{|#e`{}
yx~?p&'!"
)b)|
)|9)
?w
)|9bh
)|9+ )|9b¹
?§
)Eh+
)5@)
)5$h
)5$¹
)| +8
?µ
)E`)
)E+h
)Eb
)E+
`(¬
`(@¶
?Ø
Rozdział 1. Wprowadzenie
1.1 Wstęp
Na początku studiowania mechaniki ośrodków ciągłych pewne
trudności może nam sprawić wdrożenie się do korzystania z rachunku
tensorowego oraz zdobycie umiejętności poprawnego posługiwania się
zapisem indeksowym i absolutnym. Trudności te wynikają na ogół
z nieznajomości podstawowych pojęć i twierdzeń z algebry liniowej oraz
z braku odpowiedniego przygotowania w zakresie algebry i analizy
tensorowej.
Teoria tensorów jest teorią matematyczną, która pozwala podać
jednolity język służący do opisu własności mechanicznych, termicznych,
optycznych, elektrycznych i magnetycznych ośrodków materialnych, w tym
kryształów i tekstur. Tensory występujące w tych dziedzinach są
wykorzystywane do jawnego lub mniej jawnego opisu odwzorowań
liniowych i wieloliniowych, jak również do opisu pojęć symetrii
i niezmienniczości.
Pojęcie tensora można wprowadzić na wiele sposobów. Klasyczne
ujęcie rachunku tensorowego jest opisem układów współrzędnych i operacji
różniczkowych. Tensory jako obiekty geometryczne są wówczas
definiowane odpowiedniego wymiaru tablicami liczb, które nazywamy
reprezentacjami tensora w danym układzie współrzędnych. Przy zmianie
układu współrzędnych transformują się one w zadany sposób. Jest to tak
zwana definicja transformacyjna tensora, [9], [26]. Z drugiej strony,
z algebry liniowej wynika, że tensory można wprowadzać jako operatory
liniowe
służące do opisu odwzorowań wieloliniowych, [13], [30].
Uogólniając pojęcie wektora można tensor definiować jako element
przestrzeni liniowej odpowiedniego wymiaru, [25], [30].
Literatura dotycząca rachunku tensorowej jest dość bogata.
Wymienimy zatem jedynie podstawowe opracowania z tej dziedziny np. [1],
[12], [16], [20], [28], [37], [40], [43]. W większości monografii dotyczących
mechaniki ośrodków ciągłych na ogół materiał podstawowy jest również
poprzedzony wstępem dotyczącym rachunku tensorowego [24], [25], [38].
Przedstawiony w tym opracowaniu materiał zawiera podstawy
rachunku tensorowego w zakresie maksymalnie zbliżonym do potrzeb
mechaniki ośrodków ciągłych. Układ materiału, jak również podane w nim
informacje tworzą pewną całość i pozwalają uzyskać wiedzę z algebry
8
i analizy tensorowej w zakresie niezbędnym do swobodnego studiowania
mechaniki ośrodków ciągłych bez konieczności uzupełniania jej innymi
źródłami. Zakres przedstawionego rachunku tensorowego jest ograniczony
do potrzeb ze strony mechaniki ośrodków ciągłych.
Każdy dział mechaniki ma swój specyficzny aparat matematyczny.
Podstawowym aparatem matematycznym, który jest stosowany
w mechanice ośrodków ciągłych, jest rachunek tensorowy. Rachunek
tensorowy, dzięki swej zwięzłości, umożliwia uproszczenie zapisu
skomplikowanych operacji matematycznych będących odzwierciedleniem
geometrycznie złożonego charakteru zjawisk fizycznych i zajęcie się stroną
fizyczną tych zjawisk. A zatem, aby zająć się stroną fizyczną mechaniki
ośrodków ciągłych, należy opanować podstawy rachunku tensorowego.
Przedstawiony w tym opracowaniu materiał stanowi systematyczne
ujęcie wykładów z podstaw i zastosowania rachunku tensorowego, jakie od
wielu lat prowadzone są przez autorkę w ramach Studium Doktoranckiego
przy Instytucie Podstawowych Problemów Techniki PAN.
1.2. Podstawowe pojęcia i postulaty w mechanice ośrodków
ciągłych
Mechanika ośrodków ciągłych jest dziedziną, która sytuuje się na
skrzyżowaniu mechaniki teoretycznej, fizyki i matematyki. Powstała ona
w wyniku przyjęcia pewnych hipotez wzorowanych na newtonowskiej
mechanice punktu materialnego. Wyróżnia się jednak niezależną
aksjomatyką, specyficznymi metodami badań i odrębnym aparatem
matematycznym.
Mechanika ośrodków ciągłych zajmuje się badaniem praw
makroskopowych ruchów odkształcalnych obiektów materialnych i opisem
zachowania się tych obiektów rządzonych przez te prawa. Ze względu na
materialistyczne pojmowanie nieskończoności materii nie mogą istnieć
prawa absolutne i dlatego w mechanice ośrodków ciągłych wprowadza się
pewne obiekty modelowe dla ograniczonego zakresu zagadnień, przy
wykorzystaniu metody abstrakcji, poprzez odrzucenie czynników, pojęć
i relacji nieistotnych. Każdy model sformułowany w mechanice ośrodków
ciągłych musi mieć sprecyzowany zakres stosowalności i dokładności.
1.2. Podstawowe pojęcia i postulaty w mechanice ośrodków ciągłych
9
Kryteriami słuszności konstrukcji modelowych, jak też i źródłem ich
inspiracji, są eksperymenty. Eksperyment bez teorii, jako czyste
gromadzenie faktów, jest na ogół bezużyteczny. Należy zatem teorię
weryfikować w eksperymencie i na odwrót.
Mechanika ośrodków ciągłych zwana jest również fenomenologiczną
mechaniką ciał odkształcalnych.
Fenomenologia – z greckiego phainomenon – zjawisko, logos-nauka
jest filozoficzną nauką o fenomenach w sensie kantowskim, tj.
o zjawiskowej, empirycznej stronie rzeczywistości. Zadaniem
fenomenologii ma być „czysty opis” zjawisk rezygnujący z ich
przyczynowego wyjaśnienia. Teorie fenomenologiczne pozwalają zbadać
wiele zjawisk otaczającego nas świata, tzn. poznać przyczyny ich
powstawania i sposób ich ewolucji bez konieczności posiadania wiedzy
o zjawiskach zachodzących na poziomie molekularnym.
Fenomenologia w mechanice ośrodków ciągłych polega na takim
zastosowaniu teorii abstrakcji, gdy nie wnika się w szczegóły
mikroprocesów zachodzących w materiale na poziomie molekularnym, czy
pojedynczego kryształu opisując jedynie tzw. zjawiska makroskopowe,
obserwowane na poziomie agregatów, polikryształów. Fenomenologiczna
czarna skrzynka, do której z jednego końca wkładamy dane mikroskopowe,
pozwala z drugiego końca - wyciągać wnioski o charakterze
makroskopowym.
Mechanika ośrodków ciągłych, ze względu na rozbudowany
formalizm, jest również uważana za dział matematyki. Matematyka jest
językiem, którym posługuje się mechanika ośrodków ciągłych i jest
wykorzystywana w niej do:
• formułowania pojęć i relacji między nimi,
• sprowadzania rozpatrywanych zagadnień do poprawnie
sformułowanych problemów matematycznych,
• ścisłego
lub
przybliżonego
rozwiązywania
problemów
matematycznych, przy wskazaniu dokładności przybliżonego
rozwiązania,
• selekcji rozwiązań z punktu widzenia mechaniki.
Związek matematyki z mechaniką ma podłoże historyczne. Każdy
dział mechaniki ma swój specyficzny aparat matematyczny. I tak, np.
w mechanice bryły sztywnej wykorzystywany jest rachunek wariacyjny,
w mechanice cieczy – równania różniczkowe.
10
Podstawowym aparatem matematycznym, który jest stosowany
w mechanice ośrodków ciągłych jest rachunek tensorowy.
W mechanice ośrodków ciągłych, stosując metodę abstrakcji, z góry
rezygnujemy ze ścisłego definiowania niektórych pojęć przyjmując je jako
pierwotne wzorując się na mechanice punktu materialnego.
Przez analogie do newtonowskiej mechaniki punktu materialnego
w mechanice ośrodków ciągłych postuluje się, że
• przestrzeń fizyczna, tzn. otaczająca nas przestrzeń w której
odbywa się ruch obiektu materialnego, jest modelowana punktową
przestrzenia euklidesową;
• istnieje czas bezwzględny, pozwalający w zbiorze wszystkich
zdarzeń wyróżnić zdarzenia równoczesne z punktu widzenia
wszystkich obserwatorów w przestrzeni fizycznej. Z tych dwóch
założeń wynika istnienie absolutnego układu inercjalnego
z kartezjańską siatką;
• spełniona jest zasada przyczynowości i determinizmu zjawisk.
Zasada ta nie jest spełniona w mechanice statystycznej;
• istnieje pojęcie cząstki materialnej. Jest to najmniejsza część
ośrodka
materialnego
do
którego
odnosi
się
opis
fenomenologiczny (dla gazu będzie to porcja przewyższająca
wymiarem odległość swobodnego przebiegu molekuł, dla
monokryształu - część znaczne większa od charakterystycznego
wymiaru siatki krystalicznej, dla polikryształu - część znacznie
większa od wymiaru ziaren krystalicznych itp.);
• istnieje pojęcie ciała jako bytu abstrakcyjnego, któremu przypisuje
się pewne cechy wspólne dla wielu obiektów przyrody. Jedną
z nich jest masa ciała, inną jest miejsce zajmowane przez ciało w
przestrzeni fizycznej – geometria ciała. Proces zmiany miejsca
zajmowanego przez ciało z upływem czasu nazywamy ruchem
ciała. Ruch i deformacja ciała są skutkiem oddziaływań
zewnętrznych typu mechanicznego i termicznego. Miarą tych
oddziaływań są siły i momenty.
Ciało, rozumiane jest jako zbiór cząstek wraz z oddziaływaniami,
podczas ruchu zajmuje w przestrzeni fizycznej obszary zwarte [15]
(w sensie topologicznym) co wyraża się jako hipoteza ciągłości. Oznacza
ona, że w obszarze zajmowanym aktualnie przez ciało dowolnemu
punktowi przestrzeni fizycznej odpowiada pewna cząstka materialna. Punkt
1.3. Wybrane elementy logiki matematycznej i rachunku zdań
11
obszaru, w którym znajduje się w danej chwili cząstka, nazywamy punktem
materialnym, cały zaś obszar zajmowany przez ciało nazywamy obszarem
materialnym. Z aksjomatu ciągłości wynika, że dwie różne cząstki nie mogą
znajdować się jednocześnie w jednym i tym samym punkcie przestrzeni
fizycznej i odwrotnie, jedna i ta sama cząstka nie może znajdować się
równocześnie w dwóch różnych punktach przestrzeni fizycznej. A zatem
między cząstkami ciała a punktami obszaru zajmowanego przez to ciało
zachodzi jedno-jednoznaczna zależność. Założenie to jest dalekie od
rzeczywistości. Świadczy o tym chociażby taki fakt, że np. dla żelaza
stosunek gęstości do gęstości jąder atomowych wynosi około 10 −13 co
świadczyłoby raczej o tym, że w każdym punkcie mamy „pustkę”, która jest
niezwykle energiczna.
W mechanice ośrodków ciągłych występują takie wielkości fizyczne
jak gęstość, energia, praca itp. są to skalary wymiarowe zwane również
tensorami rzędu zerowego. Są one określone przez przypisanie im tylko
wartości liczbowej zależnej oczywiście od przyjętych jednostek. Podanie
jedynie wartości liczbowej nie wystarczy do określenia takich wielkości
fizycznych jak prędkość, siła, strumień ciepła itd. Konieczne jest dla nich
podanie kierunku w przestrzeni. Takie wielkości nazywamy wektorami lub
tensorami pierwszego rzędu. W mechanice ośrodków ciągłych występują
również takie wielkości fizyczne jak naprężenie w cząstce, odkształcenie
otoczenia cząstki. Do opisu matematycznego tych wielkości należy
wprowadzić takie obiekty geometryczne, które nazywamy tensorami
drugiego rzędu. Można je wprowadzić przez uogólnienie pojęcia wektora.
Szczególną rolę w mechanice ośrodków ciągłych odgrywają tensory
symetryczne drugiego rzędu. Im właśnie poświęcimy najwięcej uwagi.
Modelując przestrzeń fizyczną trójwymiarową punktową przestrzenią
euklidesową możemy, dla potrzeb mechaniki ośrodków ciągłych,
ograniczyć się do rozpatrywania jedynie tensorów euklidesowych, które są
elementami przestrzeni liniowych utworzonych z trójwymiarowych
wektorowych przestrzeni euklidesowych.
1.3. Wybrane elementy logiki matematycznej i rachunku
zdań
Matematyka jest nauką aksjomatyczno - dedukcyjną. Jest zatem nauką
w której przyjmuje się bez określania pojęcia pierwotne oraz bez dowodu
twierdzenia zw. aksjomatami, a następnie każde inne pojęcie, które nie jest
12
pojęciem pierwotnym definiuje się za pomocą pojęć pierwotnych, a każde
twierdzenie, które nie jest aksjomatem dowodzi się zgodnie z prawami
logiki, [27].
Przedmiotem logiki są związki między zdaniami. Zdaniem nazywamy
wypowiedz orzekającą. Można jej przypisać (w ramach danej nauki) jedną
z dwóch ocen: prawda albo fałsz – wartości logiczne zdania. Logika ustala
wartość logiczną zdań złożonych na podstawie ustalonych uprzednio
wartości logicznych zdań składowych.
W logice matematycznej występują następujące funktory:
∼
negacja (zaprzeczenie),
∧
koniunkcja (iloczyn logiczny),
∨
alternatywa (suma logiczna),
⇒
implikacja (wynikanie),
‹
równoważność ( ≡ ).
Poza funktorami w logice matematycznej występują dwa zwroty –
zwane kwantyfikatorami:
dla każdego x - kwantyfikator ogólny (duży) ∧ ,
x
istnieje takie x - kwantyfikator szczegółowy (mały)
∨.
x
Kwantyfikatory te ułatwiają ścisłe, jednoznaczne wypowiadanie zdań.
Formą zdaniową (funkcją zdaniową) z jedną zmienną określoną na
dziedzinie D , nazywamy takie wyrażenie zawierające tę zmienną, które
staje się zdaniem, gdy na miejsce zmiennej podstawimy dowolny element
zbioru D. Jeżeli formę zdaniową z jedną zmienną poprzedzimy
kwantyfikatorem odnoszącym się do tej zmiennej to otrzymamy zdanie.
Dwa zdania o tej samej wartości logicznej nazywamy równoważnymi.
W logice matematycznej posługujemy się następującą notacją:
a∈ A
a∉ A ≡ ∼ a∈ A
α⇒β
α⇔β
∨ ϕ (a)
a
element a należy do zbioru A ,
element a nie należy do zbioru A ≡ nieprawdą
jest, że element a ∈ A ,
z α wynika β ,
z α wynika β i z β wynika α ,
istnieje takie a , że zachodzi ϕ (a),
13
∨ ϕ (a)
istnieje takie a należące do A , że zachodzi ϕ (a) ,
∨ ϕ (a)
istnieje i jest jedno takie a , że zachodzi ϕ (a),
∨ ϕ (a)
istnieje i jest jedno takie a należące do A , że
∧ ϕ (a)
zachodzi ϕ (a) ,
dla każdego a zachodzi ϕ (a) ,
∧ ϕ (a)
dla każdego a należącego do A zachodzi ϕ (a) .
a∈ A
1
a
1
a∈ A
a
a∈ A
Zbiór N = {x ∈ A; ϕ ( x )} lub N = {x ∈ Aϕ (x)}
wszystkich tych x należących do A , które spełniają ϕ (x ) .
jest
zbiorem
Iloczynem kartezjański dwóch zbiorów A, B - nazywamy zbiór
A × B , którego elementami są uporządkowane pary utworzone z elementów
zbiorów A, B . Niech zbiór A będzie zbiorem elementów a, b, c,... , zaś
zbiór B będzie zbiorem elementów x, y, z ,... . Iloczynem kartezjańskim
tych zbiorów A × B jest zbiór uporządkowanych par (a, x), (b, y ), (c, z )...
Sumą prostą dwóch zbiorów A, B nazywamy zbiór U = A ⊕ B ,
którego elementy można w sposób jednoznaczny przedstawić w postaci
sumy elementów zbiorów A, B . Jeżeli element u ∈ U to istnieje
jednoznaczny rozkład tego elementu na u a i u b taki, że u = u a + u b
i u a ∈ A , u b ∈ B . I tak np. przestrzeń tensorów drugiego rzędu jest sumą
prostą przestrzeni tensorów symetrycznych i przestrzeni tensorów
antysymetrycznych.
Zaprzeczenie zdań (Prawa de Morgana):
zaprzeczenie alternatywy
∼ ( p ∨ q) ≡ (∼ p) ∧ (∼ q) ;
zaprzeczenie koniunkcji
14
∼ ( p ∧ q) ≡ (∼ p) ∨ (∼ q) ;
zaprzeczenie implikacji
∼ ( p ⇒ q) ≡ p ∧ (∼ q) ;
zaprzeczenie zdania z kwantyfikatorem
∼ ∧ ϕ (a ) ⇔ ∨ ∼ ϕ (a ) ,
a
a
∼ ∨ ϕ (a) ⇔ ∧ ∼ ϕ (a) .
a
a
Reguła odrywania (najczęściej stosowane prawo logiki)
Jeżeli prawdziwe są: implikacja p ⇒ q oraz poprzednik p , to można
z tej implikacji oderwać następnik q nadając mu samoistny byt i przyjąć
jako zdanie prawdziwe.
Prawo przechodności implikacji
Jeżeli prawdziwe są dwie implikacje: p ⇒ q i q ⇒ r to prawdziwa
jest implikacja p ⇒ r.
Warunek konieczny i warunek wystarczający
Jeżeli prawdziwa jest implikacja p ⇒ q to mówimy, że p jest
warunkiem wystarczającym dla q , natomiast q jest warunkiem
koniecznym dla p. Warunek wystarczający może nie być warunkiem
koniecznym. I tak np. symetria tensora drugiego rzędu jest warunkiem
wystarczającym na to aby jego wartości własne były rzeczywiste. Symetria
tensora nie jest jednak warunkiem koniecznym na to aby wartości własne
tensora były rzeczywiste. Warunek konieczny może nie być warunkiem
wystarczającym. I tak np. zerowanie się pierwszej pochodnej funkcji jednej
zmiennej jest warunkiem koniecznym na to aby istniało ekstremum funkcji.
Warunek ten nie jest jednak warunkiem wystarczającym. W punkcie
zerowania się pierwszej pochodnej może istnieć punkt przegęcia. Jeżeli
warunek konieczny jest jednocześnie warunkiem wystarczającym to
wówczas mówimy, że jest to warunek konieczny i wystarczający.
Każde twierdzenie matematyczne można wypowiedzieć w postaci
implikacji: jeżeli założenie to teza. W twierdzeniu założenie stanowi
warunek wystarczający na to, aby teza tego twierdzenia była prawdziwa.
Założenie to nie stanowi warunku koniecznego.
15
Twierdzenia matematyczne mają różnorodną budowę.
Jeżeli twierdzenie Z ⇒ T
jest twierdzeniem prostym, to
twierdzenie T ⇒ Z
jest twierdzeniem odwrotnym
twierdzenie ∼ Z ⇒∼ T jest twierdzeniem przeciwnym , zaś
twierdzenie ∼ T ⇒∼ Z jest twierdzeniem przeciwstawnym.
Twierdzenia proste i przeciwstawne maja taka sama wartość logiczną,
również twierdzenia odwrotne i przeciwne maja taką sama wartość
logiczną. Dowód twierdzenia prostego można zastąpić dowodem
twierdzenia przeciwstawnego.
Kwadrat logiczny stanowi zamknięty układ implikacji Rys.1. Na
przekątnych kwadratu znajdują się twierdzenia przeciwstawne. Implikacje
zaznaczone na końcach tej samej przekątnej są równoważne. Na jego
bokach natomiast są twierdzenia odwrotne i przeciwne. Prawdziwość dwóch
implikacji przy końcach jednego boku kwadratu zapewnia prawdziwość
wszystkich czterech.
Rys. 1. Zamknięty układ implikacji.
16
Z kwadratu logicznego wynika, że
(Z ⇒ T ) ⇔ (∼ T ⇒ ∼ Z ) .
Zamknięty układ twierdzeń stanowi każda z dwóch par:
{ Z ⇒ T i ∼ Z ⇒ ∼ T } , { T ⇒ Z i ∼ T ⇒ ∼ Z} .
Z prawdziwości wszystkich twierdzeń stanowiących układ zamknięty
wynika prawdziwość wszystkich twierdzeń do nich odwrotnych.
Znajomość przedstawionych elementów logiki pozwoli nam w sposób
precyzyjny formułować pewne twierdzenia i wyciągać z nich właściwe
wnioski.
Rozdział 2. Struktury algebraiczne
Przestrzeń jako pojęcie pierwotne jest jedną z form istnienia materii.
Pod pojęciem przestrzeni we współczesnej matematyce rozumie się zbiór
dowolnych obiektów, między którymi ustalone są pewne związki.
Przestrzenią fizyczną natomiast nazywamy otaczającą nas przestrzeń
w której zachodzą zjawiska fizyczne.
W wyniku bezpośredniej obserwacji otaczających nas przedmiotów
i relacji między nimi powstała koncepcja geometrii euklidesowej. Była ona
podstawą myślenia twórców mechaniki Newtona i stała się podstawą fizyki
klasycznej, przyrodoznawstwa i techniki. Geometria euklidesowa
odzwierciedla dwie relacje między obiektami: relację liniowości i relację
prostopadłości. Z pierwszą związana jest koncepcja przestrzeni liniowej, zaś
z drugą pojęcie iloczynu skalarnego.
W ten sposób powstał matematyczny model punktowej przestrzeni
euklidesowej ε 3 , której elementami są punkty jako obrazy ciał uznawanych za nieruchome i zaniedbywalnie małe. Zbiór uporządkowanych par
punktów przestrzeni punktowej z dodawaniem, mnożeniem przez liczbę
i iloczynem skalarnym tworzy przestrzeń euklidesową wektorową ∋3 , [2].
W mechanice ośrodków ciągłych postuluje się, że przestrzeń fizyczna
jest modelowana przestrzenią euklidesową punktową ε 3 , którą można
odwzorować w przestrzeń euklidesową wektorową ∋3 . Przestrzeń
euklidesowa wektorowa jest zatem przestrzenią, której elementami są
wektory i jest przestrzenią liniową nad ciałem liczb rzeczywistych
z pewnym prawem kompozycji wewnętrznej zwanej iloczynem skalarnym.
Przestrzeń fizyczna jest przestrzenia jednorodną i izotropową.
Jednorodność przestrzeni jest równoważna założeniu, że prawa fizyczne nie
zależą od miejsca wystąpienia zjawiska. Izotropowość natomiast oznacza,
że wszystkie kierunki w przestrzeni są równoważne. Z tych dwóch
własności wynika równoważność wszystkich przestrzennych układów
współrzędnych użytych do opisu badanego zjawiska. Niezmienniczość praw
fizycznych przy zmianie przestrzennych układów współrzędnych można
wyrazić stosując rachunek tensorowy. Zgodnie z podstawową własnością
rachunku tensorowego nie zachodzi potrzeba wiązania się z jakimkolwiek
układem współrzędnych.
W celu zdefiniowania przestrzeni euklidesowej wektorowej jako
tworzywa przestrzeni tensorów euklidesowych należy wprowadzić pojęcie
18
struktury algebraicznej, najprostszych struktur algebraicznych jakimi są
grupa i ciało oraz pojęcie przestrzeni liniowej, [13], [18], [30].
STRUKTURĄ ALGEBRAICZNĄ nazywamy zbiór złożony ze
skończonej liczby zbiorów oraz ze skończonej liczby odwzorowań
iloczynów kartezjańskich tych zbiorów w te zbiory. Odwzorowania
wchodzące w skład struktury nazywamy działaniami.
2.1 Pojęcie grupy i ciała
Do najprostszych struktur algebraicznych należą grupa i ciało.
Grupą nazywamy strukturę algebraiczną (G, ◊ ) , gdzie G jest zbiorem
niepustym, a działanie ◊ jest odwzorowaniem
◊ : G × G → G,
(g , h ) ∈ G × G ⇒ g ◊h ∈ G.
Działanie to spełnia następujące aksjomaty:
a) własność łączności
∧ g1◊(g 2 ◊g3 ) = (g1◊g 2 ) ◊g3 ;
g1, g2, g3∈ G
∨
b) e –element neutralny grupy
∧ e ◊g = g ◊e = g ;
∧
c) h –element odwrotny do g
∨ g ◊h = h ◊g = e.
e ∈G g ∈G
(2.1)
g ∈G h ∈G
Jeśli grupa spełnia ponadto warunek
∧ g ◊h = h ◊g
g , h ∈G
(2.2)
to nazywamy ją grupą abelową (grupą przemienną).
Przykłady grup:
1) (Z, + ) addytywna grupa liczb całkowitych (e = 0, h = − g ) ;
2) (R, + ), (R − {0}, ⋅) addytywna (e = 0, h = − g ) i multiplikatywna
(e = 1, h = g ) grupy liczb rzeczywistych;
−1
3) Zbiór wszystkich obrotów przestrzeni wokół ustalonej osi jest
grupą.
19
2.1 Pojęcie grupy i ciała
Działaniem w grupie jest składanie obrotów.
Każdy obrót można opisać wersorem k skierowanym wzdłuż osi
obrotu i kątem α o który zachodzi obrót wokół osi. Kąt α jest liczony w
kierunku, który jest dodatnim względem wersora k .
Złożeniem dwóch obrotów o kąty α i β jest obrót o kąt (α + β ) .
Obrotami wzajemnie przeciwnymi nazywamy dwa obroty w przeciwnych
kierunkach o ten sam kąt.
Jeżeli obrót wokół osi o kierunku k o kąt α oznaczymy przez Rkα to
Rkα Rkβ = Rkα +β ;
Rkα Rk−α = Rk0 .
Grupa jest jedną z najprostszych struktur algebraicznych.
Ciałem nazywamy strukturę algebraiczną (K , +, ⋅) ,
odwzorowania
+ : K × K → K ; (α , β ) ∈ K × K ⇒ α + β ∈ K ,
⋅ : K × K → K ; (α , β ) ∈ K × K ⇒ α ⋅ β ∈ K
są odwzorowaniami spełniającymi następujące aksjomaty:
a) (K , + ) jest grupą abelową;
b) (K − {0 }, ⋅) jest grupą abelową, gdzie { 0 } jest elementem
neutralnym grupy (K , + ) ;
c) rozdzielność względem dodawania
∧ α ⋅ (β + γ ) = α ⋅ β + α ⋅ γ .
gdzie
(2.3)
α , β , γ ∈K
Strukturę algebraiczną o powyższych własnościach nazywa się często
ciałem przemiennym.
Przykłady ciał:
1) (W, +, ⋅) ciało liczb wymiernych;
2) (R , +, ⋅) ciało liczb rzeczywistych;
3) (C, +, ⋅) ciało liczb zespolonych C = R × R .
Działania w C są określone następująco:
( a, b) + ( a', b' ) = ( a + a', b + b' ) ,
( a, b) ⋅ ( a', b' ) = ( aa '−bb', ab'+ a ' b) , dla ( a, b), ( a', b' ) ∈ C .
20
Ciało K nazywamy algebraicznie domkniętym (lub zupełnym) jeśli
każdy wielomian jednej zmiennej o współczynnikach z ciała K ma w ciele
K miejsce zerowe. (Zasadnicze twierdzenie algebry)
Ciało (C, +, ⋅) - liczb zespolonych jest ciałem algebraicznie domkniętym.
2.2. Przestrzenie liniowe
Bardziej złożoną strukturą algebraiczną niż grupa i ciało jest struktura
algebraiczna zwana przestrzenią liniową. Badanie tej struktury jest
przedmiotem działu algebry, który nosi nazwę algebry liniowej.
Przestrzenią liniową L nad ciałem K nazywamy strukturę
algebraiczną (L, + ; K , + , ⋅ ; ⋅) dla której:
a) (L, + ) jest grupą abelową;
b) (K , +, ⋅) jest ciałem;
c) mnożenie elementów zbioru L przez elementy zbioru K
⋅: K ×L → L
(α , A)∈K × L ⇒ α ⋅ A = α A ∈ L
(znak mnożenia został opuszczony)
spełnia aksjomaty:
∧
∧
α ∈K A, B ∈L
∧
∧
α , β ∈K A∈L
∧ ∧
α , β ∈K A∈L
∨ ∧
1∈K A∈K
α ( A + B ) = α A + α B,
(α + β ) A = α A + β A,
α (β A) = (α β )A,
(2.4)
1 A = A1 = A, 1 - element neutralny ciała K .
Przestrzenią liniową nazywamy zatem dowolny zbiór L o określonej
powyżej strukturze. Na ogół nie precyzujemy czym są elementy tego zbioru.
Przestrzeń liniową L nazywamy przestrzenią n – wymiarową
i oznaczamy przez Ln , jeżeli istnieje w niej liniowo niezależny układ rzędu
n i nie istnieje liniowo niezależny układ rzędu większego od n.
21
2.2. Przestrzenie liniowe
Układem liniowo niezależnym rzędu n nazywamy każdy zbiór n
elementów A1 , A2 ,K , An ∈ Ln taki, że z równości
α 1 A1 + α 2 A2 + K + α n An = 0
wynika, że
α1 = α 2 = K = α n = 0 .
Bazą w przestrzeni Ln nazywamy każdy liniowo niezależny układ n
elementów
A1 , A2 ,K , An ∈ Ln .
Jeżeli układ A1 , A2 ,K , An ∈ Ln jest baza w Ln , to
∧
A∈L
n
1
∨
α 1 , α 2 ,K, α n ∈K
A = α 1 A1 + α 2 A2 + K + α n An .
(2.5)
Układ A1 , A2 ,K , An generuje więc całą przestrzeń Ln . Elementy
α ,α ,K,α n ∈K
1
2
przyporządkowane są elementowi A w bazie
A1 , A2 ,K , An w sposób jednoznaczny.
Powyższe zapisy są prostsze jeżeli skorzystamy z konwencji
sumacyjnej Einsteina. Zgodnie z tą konwencją każdy jednomian w którym
dwukrotnie powtórzony jest pewien indeks, raz na poziomie dolnym i drugi
raz na poziomie górnym należy rozumieć jako sumę jednomianów
powstających z danego przez wpisanie zamiast powtarzającego się indeksu
wszystkich jego wartości od 1 do n (n – wymiar przestrzeni). Powtarzający
się indeks nazywamy niemym. Nazwę indeksu niemego można zmieniać.
Reguła ta ma charakter czysto mnemotechniczny.
Ciąg elementów A1 , A2 ,K , An można zapisać jako Ai (i – od 1 do n).
Indeks i nazywamy swobodnym.
Korzystając z konwencji sumacyjnej Einsteina możemy napisać, że
A = α 1 A1 + α 2 A2 + K + α n An = α k Ak = α m Am .
PRZESTRZENIE SPRZĘŻONE
Dwie przestrzenie liniowe o tym samym wymiarze i nad tym samym
ciałem: Ln i M n nad ciałem K nazywamy wzajemnie sprzężonymi
(dualnymi) L• n = M n , jeżeli na iloczynie kartezjańskim tych przestrzeni
22
określone jest odwzorowanie zwane operacją sprzęgającą, które jest formą
biliniową niezdegenerowaną.
Operacja sprzęgająca każdej parze elementów przyporządkowuje skalar
Ln × M n → K ,
( A, a ) ∈ L n × M n ⇒ 〈 A, a 〉 ∈ K .
Przyporządkowanie to jest liniowe względem elementów przestrzeni L n
i elementów przestrzeni M n oraz spełnia następujące warunki :
dla każdego elementu A ∈ L n , to
jeśli 〈 A, a〉 = 0
a = 0,
dla każdego elementu a ∈ M n , to A = 0.
jeśli 〈 A, a〉 = 0
W definicji tej obie przestrzenie występują równoważnie. Możemy zatem
napisać L• n = M n lub L n = M • n . Stąd wynika, że dla każdej przestrzeni
liniowej spełniona jest równość (L• n ) • = L n .
Pomimo, że przestrzenie sprzężone (dualne) występują w definicji
równoważnie, to jedna z nich jest zwykle wyróżniona z różnych powodów.
Może np. występować częściej. Nazywamy ją wówczas przestrzenią
podstawową. Oznaczymy ją przez N , a jej elementy będziemy oznaczać
przez x, ( x ∈ N ) . Bazą w tej przestrzeni będą elementy e i . Elementy
przestrzeni do niej sprzężonej będziemy oznaczać przez ς, (ς ∈ N • ) . Bazę
w tej przestrzeni będą stanowiły elementy ε α . Elementy przestrzeni
podstawowej nazywane są często wektorami, zaś elementy przestrzeni
sprzężonej kowektorami.
Operacja sprzężenia 〈x, ς〉 przypomina iloczyn skalarny i będzie z nim
utożsamiana dla przestrzeni euklidesowych 〈 x, ς〉 ≡ x ⋅ ς .
Należy jednak pamiętać, że w odróżnieniu od iloczynu skalarnego operacja
sprzężenia oznacza mnożenie elementów z dwóch różnych przestrzeni
liniowych. Elementy x, ς nazywamy ortogonalnymi, gdy x ⋅ ς = 0.
Niezdegenerowane mnożenie skalarne oznacza, że w N nie istnieje wektor
2.3. Odwzorowania struktur algebraicznych
23
niezerowy ortogonalny do całej przestrzeni N • , i analogicznie w N • nie
istnieje kowektor niezerowy ortogonalny do całej przestrzeni N .
Podstawą wielu stwierdzeń i dowodów jest następujący fakt:
jeżeli ciąg wektorów e 1 , e 2 ...., e m jest dowolną, ustaloną bazą w N , a
α 1 , α 2 ,...., α m jest dowolnym ciągiem liczb (elementem R n ) to
istnieje dokładnie jeden kowektor ς ∈ N • taki, że ς ⋅ e i = α i
( i = 1,2,...., n ) .
Dowód tego faktu wynika z równości wymiarów przestrzeni dualnych oraz
z założenia, że operacja sprzęgająca dwie przestrzenie dualne jest
niezwyrodniała.
Z podanego faktu wynika również następujący ważny wniosek:
dla każdej bazy e i w przestrzeni N istnieje dokładnie jedna baza ε j w
przestrzeni sprzężonej N • taka, że (D.1)
e i ⋅ ε j = ε j ⋅ e i = δ ij .
(2.6)
Zdefiniowaną tym wzorem bazę ε j nazywamy zwykle kobazą bazy e i .
Parę baz e i , ε j nazywamy dualną parą baz. Operowanie dualnymi parami
baz znacznie upraszcza niektóre dowody i rachunki. Np.
x ⋅ ς = ( x i e i ) ⋅ (ς j ε j ) = x i ς j (e i ⋅ ε j ) = x i ς j δ ij = x i ς i .
xi = x ⋅εi , ς i = ς ⋅ei .
Poza strukturami algebraicznymi interesują nas odwzorowania
pomiędzy tymi strukturami. Nie będą to dowolne odwzorowania ale
odwzorowania, które będą posiadały pewne własności. Będą one
mianowicie zachowywały własności tych struktur. Te szczególne
odwzorowania noszą nazwę morfizmów lub homomorfizmów struktur
algebraicznych, [13].
Dla grup, gdy (G , ◊ ) , ( H , ◊ ) są dwiema grupami, to odwzorowanie
f :G → H nazywamy homomorfizmem grup, jeżeli
∧
g , h ∈G
f ( g ◊ h ) = f ( g ) ◊ f ( h ).
24
Odwracalny
(bijektywny)
homomorfizm
grup
nazywamy
izomorfizmem. Natomiast izomorfizm grupy na siebie nazywamy
automorfizmem.
Homomorfizm
grupy
w
siebie
nazywamy
endomorfizmem. Tak więc automorfizm jest to odwracalny (bijektywny)
endomorfizm.
Podobne odwzorowania można zdefiniować dla ciał oraz przestrzeni
liniowych.
ODWZOROWANIA PRZESTRZENI LINIOWYCH
Niech Ln i N m będą dwiema przestrzeniami liniowymi nad tym
samym ciałem K .
Odwzorowanie L : Ln → N m nazywamy odwzorowaniem liniowym
(homomorfizmem), jeżeli
(2.7)
∧
∧ L(α A + β B ) = α L( A) + β L( B ) .
α , β ∈K A, B ∈ Ln
Bijektywny homomorfizm przestrzeni liniowych nazywamy
izomorfizmem. Dwie przestrzenie liniowe Ln i N m nad tym samym ciałem
K nazywamy izomorficznymi jeżeli istnieje izomorfizm tych przestrzeni na
siebie. Innymi słowy istnieje wzajemnie jednoznaczne liniowe
przyporządkowanie elementom zbioru Ln elementów zbioru N m .
Izomorficzne przestrzenie liniowe są nierozróżnialne. Są one relacjami
tej samej teorii. Każde zdanie wypowiedziane w terminach jednej
przestrzeni daje się jednoznacznie „przetłumaczyć” na język przestrzeni
izomorficznej. Każde dwie przestrzenie liniowe tego samego wymiaru są
izomorficzne.
Przykład:
Każda przestrzeń Ln nad ciałem R (liczb rzeczywistych) jest
przestrzenią izomorficzną z przestrzenią
R n = R × R × R × K× R .
Jeżeli elementy Ai (i = 1, 2, K , n ) tworzą bazę w Ln , to
1
∧ ∨
A∈ L α ∈R
i
A = α i Ai .
25
Reprezentację A w bazie Ai tworzy ciąg skalarów α i (α 1 , α 2 ,K,α n )
z R utożsamianych z elementami przestrzeni R n .
Różnica między samym elementem A ∈ L n a układem skalarów α i
należących do R jest bardzo istotna. A mianowicie, każdy układ skalarów
α i zawierający przynajmniej jeden element α k ≠ 0 jest reprezentacją
zadanego elementu A w pewnej bazie. Baz takich jest nieskończenie wiele,
jeżeli przynajmniej dwa skalary αi są różne od zera. Tzn., że
k
∧ ∧ ∨ A = α Bk A ≠ 0 .
A ∈ L α i ∈R
Bk ∈ L
FORMA LINIOWA
Szczególnym przypadkiem odwzorowania liniowego L : Ln → N m jest
odwzorowanie, gdy m=1 i przestrzeń N m = N 1 = K . Zachodzi wtedy
równość
L : Ln → N 1 = K
L ( A ) = φ ( A) = α ∈ K .
Odwzorowanie tej postaci nazywamy formą liniową φ
przestrzenią liniową Ln .
nad
ODWZOROWANIE BILINIOWE
Niech Ln , N m i M k będą przestrzeniami liniowymi nad tym samym
ciałem K .
Odwzorowanie
B : Ln × N m → M k
(A, a )∈ Ln × N m ⇒ B(A, a )∈ M k
nazywamy biliniowym, jeśli
B ( A + B , a ) = B( A, a ) + B (B , a ),
B ( A, a + b ) = B ( A, a ) + B ( A, b ),
B (β A, a ) = B ( A, β a ) = β B( A, a ),
dla każdego β ∈K , dla każdego A, B ∈ Ln i dla każdych a, b ∈ N m .
(2.8)
26
FORMA BILINIOWA
Jeżeli przestrzeń M k jest ciałem K (k=1), to odwzorowanie
B : Ln × N m → M1 = K
( A, a ) ∈ Ln × N m ⇒ B( A, a ) ∈K
nazywamy formą biliniową. W ten sposób można definiować
odwzorowania wieloliniowe i formy wieloliniowe.
SUMA PROSTA PRZESTRZENI LINIOWYCH
Najprostszym przykładem budowania, w oparciu o znane przestrzenie
liniowe nad tym samym ciałem K , nowej przestrzeni liniowej jest suma
prosta.
W celu zdefiniowania sumy prostej podajemy definicję sumy
algebraicznej, [13].
Niech ν1 i ν2 będą podzbiorami przestrzeni liniowej Ln . Zbiór
ν + ν = { A + A ∈L ; A ∈ν , A ∈ν }
1
2
1
2
n
1
1
2
2
nazywamy sumą algebraiczną podzbiorów ν1 i ν2 .
Sumę algebraiczną podprzestrzeni ν1 i ν2 nazywamy sumą prostą
ν1 ⊕ ν2 , jeżeli każdy element sumy daje się jednoznacznie przedstawić w
postaci sumy elementów przestrzeni ν1 i ν2 .
Sumą prostą przestrzeni liniowych Ln i N m nad tym samym ciałem
K nazywamy przestrzeń M n + m = Ln ⊕ N m powstającą z iloczynu
kartezjańskiego Ln × N m przez zdefiniowanie w tym zbiorze operacji
dodawania i mnożenia przez elementy ciała K tak, że
∧
A, B ∈ Ln
∧
∧
a , b ∈N m α , β ∈K
α ( A, a ) + β ( B , b ) = (α A + β B , α a + β b ),
M n + m - przestrzeń liniowa.
(2.9)
27
2.4. Przestrzenie euklidesowe
Każdy element przestrzeni Ln ⊕ N m daje się jednoznacznie
przedstawić w postaci sumy elementów przestrzeni Ln i N m . Wymiar
przestrzeni Ln ⊕ N m wynosi n+m.
ILOCZYN TENSOROWY PRZESTRZENI LINIOWYCH
Iloczynem tensorowym przestrzeni liniowych Ln i N m nad tym
samym ciałem K nazywamy przestrzeń liniową M n•m = Ln ⊗ N m powstającą
z iloczynu kartezjańskiego Ln × N m . Wymiar przestrzeni Ln ⊗ N m wynosi
n⋅m.
Przyporządkowanie
⊗ : Ln × N m → Ln ⊗ N m ,
(A, a )∈ Ln × N m ⇒ A ⊗ a ∈ Ln ⊗ N m
jest przykładem odwzorowania biliniowego.
Spełnia zatem następujące aksjomaty:
∧
A∈Ln
∧
A, B ∈Ln
∧
A∈Ln
∧
a , b∈N m
∧
a∈N m
∧
b∈N m
A ⊗ (a + b ) = A ⊗ a + A ⊗ b ,
( A + B ) ⊗ a = A ⊗ a + B ⊗ a,
∧
α ∈K
(2.10)
α A ⊗ b = A ⊗ α b = α ( A ⊗ b ).
Przestrzenią euklidesową wektorową ∋ n nazywamy n – wymiarową
przestrzeń liniową (2.4) nad ciałem liczb rzeczywistych R , w której
dodatkowo jest zdefiniowana operacja iloczynu skalarnego. Elementami
przestrzeni są wektory a , b ,K [29].
Iloczynem skalarnym nazywamy formę biliniową taką, że
⋅ : ∋ n × ∋ n → 9,
(2.11)
(a, b ) ∈∋ n × ∋ n ⇒ a ⋅ b ∈ 9.
Jest to prawo kompozycji przyporządkowujące dwóm wektorom
skalar (liczbę). Odwzorowanie to spełnia następujące aksjomaty:
1. ∧ a ⋅ b = b ⋅ a,
a, b ∈∋ n
28
2.
3.
4.
a ⋅ (b + c ) = a ⋅ b + a ⋅ c,
∧
a, b, c ∈∋n
∧
∧
a, b ∈∋ n
∧
a ∈∋ n
α ∈R
(a + b ) ⋅ c = a ⋅ c + b ⋅ c,
α a ⋅ b = α (a ⋅ b ) = a ⋅ (α b ),
a ⋅ a ≥ 0 i a ⋅ a = 0 dla a = 0.
Normą – modułem wektora a nazywamy liczbę a o własnościach:
1
a = a = (a ⋅ a ) 2 ,
a ≥0
a = 0 dla
a = 0,
αa = α a
∧
a, b ∈∋ n
a+b ≤ a + b
(nierówność Schwartza) .
Wektor a, dla którego a = 1 nazywamy wersorem.
Kąt ϕ , który jest kątem między wektorami a i b wyznaczamy ze
wzoru
cos ϕ =
a⋅b
, 0 ≤ϕ ≤π .
a b
(2.12)
Jeżeli wektory ei (i = 1,2...n ) są bazą w ∋ n , to generują one całą
przestrzeń.
W mechanice ośrodków ciągłych interesuje nas głównie przestrzeń
euklidesowa trójwymiarowa ∋3 (∋ n dla n = 3) tzn. przestrzeń wektorowa
euklidesowa, w której bazą jest dowolna trójka liniowo niezależnych
wektorów. Jeżeli wektory e i (e1 , e 2 , e 3 ) są bazą w ∋3 , to
∧
a ∈∋
1
n
∨
α ,α ,α
1
2
3∈R
a = α 1e1 + α 2 e 2 + α 3e 3 = α k e k .
Trójkę liczb α i , przyporządkowaną jednoznacznie wektorowi a
w bazie e i , nazywamy reprezentacją wektora a w tej bazie. Jeżeli baza e i
29
jest ustalona, to wektor a można utożsamić z jego reprezentacją, tzn.
z trójką liczb α i . Należy pamiętać, że te trójki liczb przyporządkowane
temu samemu wektorowi w różnych bazach będą inne. Zachodzi zatem
zależność
∧
a≠0 ∈∋3
∧
α, β , γ ∈R
∨
g k∈∋3
a = α g1 + β g 2 + γ g 3 ,
a więc każda trójka liczb takich, że przynajmniej jedna z nich jest różna od
zera, może być reprezentacją zadanego wektora w odpowiednio dobranej
bazie.
Przestrzeń euklidesowa ∋ 3 jest przestrzenią liniową, posiada zatem
wszystkie własności przestrzeni liniowych.
Dla przestrzeni euklidesowej ∋3 operacja iloczynu skalarnego jest
formą biliniową, a więc może być uznana za operację sprzęgającą
przestrzeń euklidesową ze sobą samą.
Jeżeli ∋3∗ jest przestrzenią sprzężoną (dualną) do przestrzeni ∋3 , to
przestrzenie te są izomorficzne. Na tej podstawie przyjmuje się, że ∋3∗ =∋3 .
Pomimo przyjęcia takiego założenia pozostawiamy, ze względów
rachunkowych, pojęcie bazy i kobazy jako baz w tej samej przestrzeni
euklidesowej ∋3 .
Kobazą bazy e i nazywamy taką bazę e j , dla której
1 dla i = j ,
(delta Kronecker'a) δ i j = 
.
0
dla
i
≠
j

≡ e m ⋅ e n nazywamy macierzą metryczną. Dla danej bazy
ei ⋅ e j = δ i
Macierz g mn
j
e i jej kobaza e j jest wyznaczona jednoznacznie
e j = g jk e k , ( gdzie
g jk = e j ⋅ e k ).
Współczynniki g jk ≡ e j ⋅ e k rozkładu kobazy e j
wyznaczamy z układu równań liniowych Cramer'a
g jk g km = δ j m .
(2.13)
w bazie e k
30
Kobaza e j jest bazą w
w kobazie e
∋3 .
Można zatem wektory e j rozłożyć
k
e j = g jk e k .
(2.14)
Ze wzorów (2.13), (2.14) wynikają pewne własności macierzy
g
i g mn . Są to współczynniki rozkładu jednej bazy w drugiej. Służą one
do podnoszenia i opuszczania indeksów.
Dowolny wektor a ∈∋ 3 można rozłożyć w bazie e k lub kobazie e j , a
mianowicie
a = α k ⋅ ek = α j ⋅ e j .
jk
Po wykorzystaniu wzorów na rozkład jednej bazy w drugiej
otrzymujemy, że
α k = a ⋅ e k = α j g jk ,
(2.15)
α j = a ⋅ e j = α k g kj .
Wybór bazy w
∋3
jest dowolny. Jeżeli hα stanowi inną bazę od e i , to
jeżeli
hα ⋅ h β = δ α
β
wówczas wektory h β są kobazą do hα . Każda z baz e i , e j , hα , h β generuje
całą przestrzeń. Wektor a można wówczas rozłożyć w każdej z tych baz
a = α~α hα = α~β h β = α k e k = α j e j , hα = g i α e i = gα j e j .
Stąd wynika, że
e i = (e i ⋅ hα ) hα = (e i ⋅ h β ) h β = g i hα = g iβ h β ,
α
e j = (e j ⋅ hα ) hα = (e j ⋅ h β )h β = g j α hα = g jβ h β .
(2.16)
Współczynniki rozkładu wektorów jednej bazy w drugiej są
iloczynami skalarnymi odpowiednich wektorów bazowych, które można
uznać za definicję tych obiektów liczbowych. Jeżeli bazy są ustalone, to ich
iloczyny skalarne są niezmiennikami.
31
Iloczyn
następująco:
skalarny
dwóch
wektorów
a i b ∈∋ 3
realizuje
się
a ⋅ b = α k e k ⋅ β m e m = α k β m e k ⋅ e m = α k β m g km = α j e j ⋅ β m e m = α j β m e j ⋅ e m = α j β m g jm =
= α j e j β m e m = α j β m e j ⋅ e m = α j β mδ j m = α j β j = α j β j .
Przestrzeń euklidesową punktową ε n o wymiarze n definiuje się jako
zbiór elementów (punktów) takich, że każdej uporządkowanej parze
punktów A, B ∈ε n przyporządkowany jest jednoznacznie wektor AB ∈∋ n .
Przestrzeń euklidesowa punktowa ε n związana jest z przestrzenią
euklidesową wektorową ∋ n przez zadane odwzorowanie:
ε n × ε n →∋ n ;
( A, B ) ∈ ε n × ε n ⇒ AB ∈∋ n .
Odwzorowanie to spełnia następujące aksjomaty:
∧
A, B∈ε
AB=−BA
n
∧
A, B, C∈εn
AB= AB+BC
∧ ∧ ∨
O∈εn X∈εn x∈εn
OX=x,
gdzie x – promień wektor punktu X względem wybranego punktu O.
Obierając w ε n punkt O można zdefiniować jedno-jednoznaczne
przyporządkowanie
o
ϕ :εn
→
∋n ,
o
ϕ ( X ) = OX = x
(2.17)
pomiędzy punktami z ε n a wektorami z ∋ n .
Przestrzeń ε n nie jest przestrzenią liniową. Można jednak przenieść
do niej struktury przestrzeni wektorowej jako odpowiednie operacje na
promieniach wodzących. Struktura ta zależy od wyboru punktu O.
32
Reperem w przestrzeni punktowej
εn
stowarzyszonej z
∋n
nazywamy
każdą parę (O; e i ) , gdzie O ∈ ε n , e i ∈∋ n . Punkt O jest punktem zaczepienia
repera, zaś wektory e i są bazą w ∋ n .
Baza e i jest ortonormalna, gdy e i ⋅ e j = δ ij . Wektory bazy są
wówczas wzajemnie ortogonalne i są wersorami.
W mechanice ośrodków ciągłych przyjmuje się, że przestrzeń fizyczna
jest modelowana trójwymiarową punktową przestrzenią euklidesową ε 3 z
reperem (O; e i ) (i=1,2,3).
Przestrzeń euklidesową punktową ε 3 definiuje się czasem jako zbiór
R 3 = R × R × R , gdzie R jest ciałem liczb rzeczywistych.
Wybierając w ∋3 bazę ortonormalną i k ( i k ⋅ i l = δ kl ) otrzymujemy
wzajemnie jednoznaczne odwzorowanie
3
ik ψ : ∋ 3 → R
(2.18)
(
)
(
)
ψ
x
=
x
⋅
i
,
x
⋅
i
,
x
⋅
i
.
ik
1
2
3
Odwzorowanie
Φ =i ψ o o ϕ :
k
ε
3 →
R3
jest izomorfizmem ε 3 w R 3 zależnym od repera (O; i k ) względem struktur
przeniesionych z ∋3 , [30].
Rozdział 3. Tensory euklidesowe
3.1. Przestrzenie tensorowe
Podstawowym obiektem naszych zainteresowań z punktu potrzeb
mechaniki ośrodków ciągłych są tensory euklidesowe [25], [30].
Tensory euklidesowe są elementami przestrzeni liniowych
utworzonych z przestrzeni euklidesowych wektorowych. A zatem
tworzywem tych przestrzeni są przestrzenie euklidesowe ∋ n .
W naszych rozważaniach ograniczamy się do przestrzeni
euklidesowych ∋3 – przestrzeni trójwymiarowych i przestrzeni tensorowych
utworzonych z tych przestrzeni.
Jako jeden z przykładów odwzorowań przestrzeni liniowych był
wprowadzony iloczyn tensorowy tych przestrzeni. Można zatem
rozpatrywać również iloczyny tensorowe dwóch przestrzeni wektorowych
euklidesowych
(1)
(2)
∋3 i ∋3 .
Iloczynem tensorowym
(1)
(2)
∋3 ⊗ ∋3
nazywamy przestrzeń T
2
o wymiarze
3 ⋅ 3 = 3 = 9 , którą otrzymujemy w wyniku odwzorowania
2
(1)
(2 )
(1)
(2 )
⊗ : ∋3× ∋3 → ∋3 ⊗ ∋3 = T 2
(1)
(2 )
(a, b ) ∈ ∋ 3 × ∋ 3
(1)
(3.1)
(2 )
⇒ a ⊗ b ∈ ∋3 ⊗ ∋3 = T 2.
Jest to odwzorowanie biliniowe (2.8).
Tensorem euklidesowym o walencji 2 (rzędu 2) nazywamy każdy
element przestrzeni liniowej T 2 (T ∈ T 2 ) .
Tensory postaci T = a ⊗ b ≠ b ⊗ a nazywamy diadami albo tensorami
rozkładalnymi. Nie każdy tensor drugiego rzędu można przedstawić w
postaci diady. Każdy natomiast jest kombinacją liniową diad. Wynika to z
faktu, że w przestrzeniach wektorowych ∋3 istnieją bazy. W każdej z
mnożonych tensorowo przestrzeni
(1)
(2)
∋3 i ∋3
mogą być różne.
Niech ei i hα będą różnymi bazami odpowiednio w
(1)
(2)
∋3 i ∋3 .
34
Układ dziewięciu diad postaci ei ⊗ hα jest bazą w T 2 . Z definicji
przestrzeni T 2 wynika wówczas, że
∧
T ∈T
1
∧
ei ⊗hα
∨
T iα ∈ R
T = T iα e i ⊗ hα .
(3.2)
2
Na ogół przyjmuje się, że w każdej z przestrzeni
(1)
(2)
∋3 i ∋3
bazy są te same.
Niech e i i e j ( ei e j = δ i ) będą bazą i kobazą, wówczas cztery układy
dziewięciu następujących diad:
j
ei ⊗ e j , ei ⊗ e j , ei ⊗ e j , ei ⊗ e j
i, j = 1, 2, 3
są czterema różnymi bazami (polibazami) w T 2 . Polibazy, w których
występują wektory należące do jednej bazy i jej kobazy nazywamy
polibazami prostymi. Oczywiście nie tylko polibazy są bazami w T 2 .
Dowolny układ dziewięciu tensorów liniowo niezależnych H k można
przyjąć jako bazę w T 2 . Można wówczas napisać T = T k H k (k=1,2,…,9).
W polibazach prostych tensor T ∈ T 2 można w sposób jednoznaczny
przedstawić w postaci
j
T = T ij e i ⊗ e j = T i j e i ⊗ e j = Ti e i ⊗ e j = Tij e i ⊗ e j ,
∧
T ∈T 2
(3.3)
i, j = 1, 2, 3.
Układy dziewięciu liczb T ij , T i j , Ti j , Tij nazywamy składowymi lub
reprezentacją tensora T w odpowiedniej polibazie. Składowe te nie są
niezależne. Ze wzorów na rozkład bazy w kobazie (2.13) i na odwrót (2.14)
otrzymujemy, że na przykład
j
Tij = Tk g ki = Tkl g ki g lj = T i k g kj ,
(3.4)
k
Tij = Ti g kj = T kl g ki g lj = T k j g ki .
Wybór bazy w przestrzeni euklidesowej jest dowolny. Jeżeli hα i h β
są inną niż ei i e j bazą i kobazą w
wówczas układy diad:
∋3 , to polibazami prostymi w
T 2 są
35
3.1. Przestrzenie tensorowe
h α ⊗ h β , h α ⊗ h β , hα ⊗ h β , h α ⊗ h β
(α , β = 1,2,3),
z których każda generuje całą przestrzeń T 2 . Tensor T ∈ T 2 można zatem
przedstawić również w postaci
~
~
~β
~
T = T αβ hα ⊗ h β = T α β hα ⊗ h β = Tα hα ⊗ h β = Tαβ hα ⊗ h β .
Łatwo pokazać, że między składowymi tensora T w różnych polibazach
(2.16) zachodzą zależności:
(
(
)(
)
)
~
T αβ = hα ⋅ e i h β ⋅ e j T ij = g α i g β j T ij ,
~
T α β = hα ⋅ e i (h β ⋅ e j ) T ij = g α i g β j T ij .
(3.5)
TENSOR METRYCZNY
Istotną rolę w rachunku tensorowym odgrywa tensor metryczny G .
Jest to tensor drugiego rzędu G ∈ T 2 o własnościach
(
)
(
)
(
)
(
)
G = ei ⋅ hα ei ⊗hα = ei ⋅ hβ ei ⊗hβ = ei ⋅ e j ei ⊗e j = hα ⋅ hβ hα ⊗hβ =
= δ i j ei ⊗e j = δ α β hα ⊗hβ ,
(3.6)
G = ei ⊗ei = hα ⊗hα = e1 ⊗e1 + e2 ⊗e2 + e3 ⊗e3 = h1 ⊗h1 + h2 ⊗h2 + h3 ⊗h3.
W dowolnej polibazie prostej mieszanej, tzn. utworzonej z wektorów bazy i
kobazy, tensor metryczny G ma reprezentację w postaci delty Kronecker’a
δ ij (D.1).
Tworząc iloczyny tensorowe więcej niż dwóch przestrzeni
euklidesowych otrzymujemy przestrzenie tensorowe tensorów wyższego
rzędu.
Tensorem euklidesowym rzędu p (o walencji p) nazywamy każdy
element przestrzeni liniowej T p o wymiarze 3 p , która powstała z iloczynu
tensorowego p przestrzeni euklidesowych
(1)
(2)
(3)
∋3 , a mianowicie
( p)
p (n )
T p = ∋3 ⊗ ∋3 ⊗ ∋3 ⊗ K ⊗ ∋3 = ⊗ ∋3 .
n =1
36
Stąd wynika, że przestrzenie:
T o = R o wymiarze 30 = 1
T 1 =∋ 3
jest przestrzenią liczb rzeczywistych,
31 = 3
o wymiarze
jest przestrzenią euklidesową wektorową,
T 2 =∋ 3 ⊗ ∋ 3 o wymiarze 3 = 9 jest przestrzenią tensorów drugiego
rzędu.
A zatem liczby można nazywać tensorami rzędu 0, a wektory tensorami
rzędu 1.
Przyporządkowanie
2
(1)
(2)
( p)
(3)
∋3 × ∋3 × ∋3 × K × ∋3 → T p
jest przyporządkowaniem p – liniowym. Każdemu ciągowi p elementów
a1 , a 2 ,K, a p ; aν ∈∋ (ν ) przyporządkowujemy element
3
a1 ⊗ a 2 ⊗ K ⊗ a p ∈ T p .
(3.7)
Tensory tej postaci nazywamy tensorami rozkładalnymi. Nie każdy
element T p jest tensorem rozkładalnym. Drugi typ tensorów stanowią
tensory będące kombinacją liniową tensorów rozkładalnych. Jeżeli w każdej
j
przestrzeni ∋( ν ) weźmiemy taką samą bazę ei i kobazę e j ( ei ⋅ e j = δ i ), to
3
polibaza prosta postaci
ei ⊗ e j ⊗ e k ⊗ K ⊗ e m
144424443
p
jest bazą w T p .
Zachodzi wówczas równość
∧
T ∈T
p
∧
e ⊗e ⊗K⊗e
i
j
∨
1
m
Ti j k ...m
T = Ti
j
k ...
m
ei ⊗ e j ⊗ ek ⊗ K ⊗ em .
1444
424444
3
p
Tensory są zatem jednością bazy (polibazy – stowarzyszenia bazowego)
i składowych w tej bazie.
37
3.2. Działania na tensorach
Dwa tensory A i B ∈ T p są sobie równe, jeżeli w tej samej polibazie
maja takie same
ei ⊗ e j ⊗ K ⊗ e k .
składowe,
tzn.,
że
Ai jKk = B i jKk
w
polibazie
Odwzorowania liniowe przestrzeni liniowych dotyczą również
przestrzeni tensorowych.
Na tensorach o dowolnej walencji (dowolnego rzędu) można
dokonywać odpowiednich operacji o ile nie są one sprzeczne z definicją
tensora.
Działania na tensorach można rozpatrywać jako odwzorowania
przestrzeni tensorowych.
a) Iloczyn tensorowy (iloczyn zewnętrzny) przestrzeni tensorowych
jest odwzorowaniem biliniowym
⊗ : T p × T q → T p ⊗ T q = T p+q ,
(3.8)
które dla tensorów rozkładalnych (3.7) realizuje się w następujący sposób:
⊗ : c ⊗ d ⊗K⊗ h ∈T p 
 ⇒ c ⊗ d ⊗ K ⊗ h ⊗ a ⊗ b ⊗ K ⊗ g ∈ T p+q .
a ⊗ b ⊗ K ⊗ g ∈ Tq 
Jeżeli tensory A, B ∈ T p i C, D ∈ T q , to
(α A + β B ) ⊗ (γ C + ξ D) = α γ A ⊗ C + α ξ A ⊗ D + β γ B ⊗ C + β ξ B ⊗ D .
Dla tensorów nierozkładalnych dowolnym tensorom T ∈ T p i P ∈ T q ,
które w odpowiednich polibazach prostych mają postać
T = T i jKm ei ⊗ e j ⊗ K ⊗ e m ,
1442443
p
P = Psu
Kn
e ⊗ e ⊗ K ⊗ en .
1442443
s
u
q
operacja ich iloczynu tensorowego jest tensorem postaci
38
Kn
S = T ⊗ P = T i jKm Psu ei ⊗ e j ⊗ K ⊗ e m ⊗ e s ⊗ eu ⊗ K ⊗ e n .
14243 144444424444443
p +q
liczby
Operacja iloczynu
T ⊗ P ≠ P ⊗ T.
tensorowego
nie
jest
przemienna.
Na
ogół
Przykłady:
1) Iloczyn tensorowy dwóch wektorów u, v ∈∋3
u ⊗ v = u i e i ⊗ vm e m = u i vm e i ⊗ e m
jest tensorem drugiego rzędu zwanym diadą.
2) Iloczyn tensorowy tensora drugiego rzędu T i wektora u
T ∈ T 2 , u ∈∋ 3
j
j
T ⊗ u = Ti e i ⊗ e j ⊗ u m e m = Ti u m e i ⊗ e j ⊗ e m
jest tensorem trzeciego rzędu.
Operacja iloczynu tensorowego realizuje się zatem przez dopisanie do
siebie stowarzyszeń bazowych i wymnożeniu liczb – reprezentacji tych
tensorów w wybranych polibazach.
b) Zwężenie tensora (kontrakcja)
Operacja zwężenia tensora T ∈ T p jest odwzorowaniem liniowym
T p → T p−2
( µ ,ν )
~ : T p → T p −2 ,
( µ ,ν )
(ν , µ )
~ = ~ ,
(3.9)
p
( µ ,ν )

~
T ∈ T p −2 .


(T ∈ T ) ⇒ 
Operacja zwężenia dla tensora rozkładalnego (3.7) realizuje się w
następujący sposób:
(ν , µ )
~→(f ⋅ d ) a⊗ b⊗ K ⊗ h 
a⊗ b⊗ K ⊗ f ⊗ K ⊗ d⊗ K ⊗ h 


p
p −2 
ν
1
2
µ
1 2
39
i polega na wymnożeniu skalarnym wektorów stojących na miejscach ν , µ
w ciągu p wektorów. Jest to operacja przemienna, ponieważ iloczyn
skalarny jest przemienny. Jest to również operacja liniowa, ponieważ
(ν , µ )
~
(ν , µ )
~
(ν , µ )
~
(α A + β B ) = α A + β B .
Dla tensorów nierozkładalnych, dla dowolnego tensora T ∈ T p postaci
µ
T = T i jK
Kν Km
ei ⊗ e j ⊗ K ⊗ eµ ⊗ K ⊗ eν ⊗ K ⊗ em
( µ ,ν )
(
)
~
ν
µ
µ
T = T i jK Kν Km e µ ⋅ eν ei ⊗ e j ⊗ K ⊗ em = T i jK Kν Km δ µ ei ⊗ e j ⊗ K ⊗ em =
µ
= T i jK
Kµ Km
ei ⊗ e j ⊗ K ⊗ e m .
A zatem dla dowolnego tensora T ∈ T p danego w polibazie prostej
operacji zwężenia po parze indeksów ( µ ,ν ) dokonujemy wymnażając
skalarnie wektory ze stowarzyszenia bazowego stojące na miejscach µ i ν .
W reprezentacji tensora dokonujemy sumowania po parze powtarzających
się wskaźników. Dla tensora o walencji p>2 operacja zwężenia nie jest
jednoznaczna i wymaga podania indeksów µ i ν po których dokonujemy
zwężenia.
 p
( p − 1) p
p!
Dla tensorów rzędu p można dokonać   =
zwężeń.
=
  2! ( p − 2 )!
2
 2
Rząd otrzymanego tensora jest o 2 niższy od rzędu tensora zwężanego.
Jeżeli wynik zwężenia jest tensorem o walencji nie mniejszej niż 2 można
dokonać dalszych zwężeń.
Przykłady:
1) Dla tensora trzeciego rzędu T ∈ T 3 operacji kontrakcji (zwężenia)
można dokonać na trzy sposoby. W wyniku zwężenia otrzymuje
się trzy różne wektory.
k
Jeżeli T = T i j ei ⊗ e j ⊗ e k , to w wyniku zwężenia otrzymujemy
następujące trzy wektory:
40
(i , j )
~
k
T1 = T = T i i e k ,
( j,k )
~
j
T2 = T = T i j e i ,
(i , k )
~
k
k
T3 = T = T i j (ei ⋅ e k ) ⊗ e j = T i j g ik e j = T i ji e j .
2) Zwężenie tensora drugiego rzędu T ∈ T 2 jest określone
~
jednoznacznie i daje skalar T ∈ R , który nazywamy śladem
~
tensora T = tr (T ) , a mianowicie
~
j i
i
1
2
3
tr (T ) = Ti e ⊗ e j = Ti = T1 + T2 + T3 .
(3.10)
(
)
Tensory bezśladowe tzn. tensory, dla których tr (T ) = 0 nazywamy
dewiatorami.
Następne operacje na tensorach są złożeniem działań iloczynu
tensorowego i zwężenia.
c) Nasunięcie tensorów (iloczyn wewnętrzny tensorów)
Jest to odwzorowanie
T p × T q → T p +q−2 ,
(3.11)
które jest złożeniem odwzorowań (3.8) i (3.9):
⊗ : T p × T q → T p+q i
(µ ,ν )
~ : T p+q → T p+q−2
(µ ,ν )
~
(A, B ) ∈ T p × T q ⇒ A ⊗ B ∈ T p+ q−2
0<µ ≤ p
p + 1 ≤ ν ≤ p + q.
Nasunięcie dwóch tensorów zwane również ich iloczynem
wewnętrznym jest tensorem, który otrzymujemy dokonując zwężenia
iloczynu zewnętrznego tych tensorów względem wskaźników, z których
jeden należy do jednego tensora a drugi do drugiego. W wyniku nasunięcia
tensorów A ∈ T p i B ∈ T q można uzyskać p ⋅ q różnych tensorów o
(µ ,ν )
~
walencji p + q − 2 postaci W = T ⊗ P .
41
( p , p +1)
~
Nasunięcie, w którym µ = p, ν = p + 1 A ⊗ B ≡ A B nazywamy
nasunięciem prostym. Jest to nasunięcie dokonane po najbliższych
indeksach. Na ogół A B ≠ B A , operacja nasunięcia prostego nie jest
przemienna.
Nasunięciem pełnym dwóch tensorów nazywamy odwzorowanie:
T p × T q → T p−q p ≥ q. Jest to procedura q – krotnego nasunięcia tych
tensorów według wzoru:
( p + 1 − q, p + 1)( p + 2 − q, p + 2)K( p, p + q )
~
A ⋅ B = A ⊗ B.
(3.12)
Gdy p = q nasunięcie pełne A ⋅ B jest skalarem, który nazywamy
iloczynem skalarnym tych tensorów. Przestrzeń tensorów, po zdefiniowania
iloczynu skalarnego, staje się przestrzenią euklidesową.
Przykłady:
1) Nasunięcie tensora drugiego rzędu T ∈ T 2 i wektora a ∈∋ 3 .
W wyniku ich nasunięcia otrzymujemy dwa różne wektory:
(ν , 3)
~
b (ν ) = T ⊗ a
(1, 3)
~
( 2 , 3)
~
b (1) = T ⊗ a, b ( 2) = T ⊗ a .
( 2 , 3)
~
Nasunięcie T ⊗ a = T ⋅ a = T a jest jednocześnie prostym i pełnym
nasunięciem tensora T i wektora a.
2) Nasunięcia dwóch diad T = a ⊗ b i P = c ⊗ d można dokonać na
cztery sposoby:
42
( µ ,ν )
~
W = a ⊗ b ⊗c ⊗d 1 ≤ µ ≤ 2 i 3 ≤ ν ≤ 4
W(1) = (a ⋅ c)b ⊗d, W(2) = (a ⋅ d)b ⊗c, W(3) = (b ⋅ c)a ⊗d, W(4) = (b ⋅ d)a ⊗c.
W wyniku nasunięcia prostego tych diad otrzymujemy tensor W ( 3) .
Nasunięciem pełnym tych diad jest skalar (a ⋅ c )(b ⋅ d ).
TWIERDZENIE 3.1
Jeżeli odwzorowanie L : T p → T q jest liniowe, to istnieje określony
jednoznacznie tensor L ∈ T p + q taki, że
∧
L (T ) = L ⋅ T ∈ T q .
T ∈T p
(3.13)
Z twierdzenia tego wynika, że liniowe odwzorowanie (L : T p → T q )
można utożsamić z tensorem L o walencji p + q . Odwzorowanie to
realizuje się przez nasunięcie pełne (3.12) tensorów L i T ∈ T p
L (T ) = Lij ..rk
m
Kn
n
T k mK ei ⊗ e j ⊗ K ⊗ e r .
1442443
q
Każdy endomorfizm L : T p → T p realizuje tensor L o walencji
parzystej ( 2 p ) .
Przykłady:
1) Odwzorowanie liniowe przestrzeni wektorowej w przestrzeń liczb
rzeczywistych
φ : T1 → T 0
a ∈ T 1 =∋ 3
φ (a ) = α ∈ T 0 = R
Jeżeli odwzorowanie jest liniowe, to
∨ ∧
ν ∈∋3 a ∈∋3
φ (a ) = ν ⋅ a = α (ν ) .
Wektor ν dla każdego operatora φ jest określony jednoznacznie.
43
2) Odwzorowanie liniowe przestrzeni wektorowej w przestrzeń
wektorową
L : T 1 → T 1 ≡∋ 3 →∋ 3
L (a ) = b ∈∋ 3 .
Odwzorowanie liniowe przestrzeni wektorowej
∋3
w siebie
nazywamy endomorfizmem albo afinorem. Istnieje tensor A ∈ T2 określony
jednoznacznie taki, że
∨
A ∈T 2
Afinory
∧
a ∈T 1
L (a ) = A ⋅ a ∈ T 1 =∋ 3 .
w
∋3 
→
∋3 oznaczamy przez
A.
Afinory – odwzorowania liniowe przestrzeni wektorowych ∋3
będziemy utożsamiać z tensorami drugiego rzędu (tensorami o walencji 2).
Afinor A jest afinorem tożsamościowym, jeżeli
∧
a∈∋3
A ⋅ a = a wówczas
A = 1 i nazywamy go tensorem jednostkowym A = 1. Można pokazać, że
tensor metryczny (3.6) jest afinorem tożsamościowym G = 1.
TWIERDZENIE 3.2
Jeżeli odwzorowanie B : T p × T q → T m jest biliniowe, to istnieje
określony jednoznacznie tensor L ∈ T p + q + m taki, że
B (A, B ) = L ⋅ (A ⊗ B ) ∈ T m .
Jest to pełne nasunięcie (3.12) tensora L i tensora A ⊗ B.
d) Transpozycja tensora
Operacja transpozycji tensora T ∈ T p po parze indeksów jest operacją
liniową odwzorowującą przestrzeń tensorów T p w siebie
( µ ,ν )
Τ
: T p →T p .
Dla tensorów rozkładalnych operacja transpozycji realizuje się przez
przestawienie wektorów stojących na miejscach µ i ν w ciągu p
wektorów, a mianowicie
 c⊗ K ⊗ a⊗ K ⊗ b⊗ K ⊗ d 
µ
ν
p
1
(µ ,ν )
T
=  c⊗ K ⊗ b⊗ K ⊗ a⊗ K ⊗ d .
µ
ν
p
1
(3.14)
44
Wynik takiego odwzorowania nazywamy izomerem.
Operacji transpozycji dla tensora o walencji p można dokonać na
 p  ( p − 1) p
 =
sposoby.
 
2
2
Dla tensorów nierozkładalnych operacji transpozycji dokonujemy
przez przestawienie w polibazie wektorów znajdujących się na miejscach
µ iν
( µ,ν )
(
) = (T
)
( µ,ν )
µ
n i
i ...ν...
T =T
T
ν
e ⊗eµ ⊗K⊗e ⊗K⊗en
T
µ n i
i ...ν...
e ⊗eν ⊗K⊗eµ ⊗K⊗en .
Dla tensora drugiego rzędu operacja transpozycji
jednoznacznie
j
TΤ = Ti ei ⊗ e j Τ = T j i ei ⊗ e j .
(
jest
określona
)
Częścią symetryczną tensora T po parze ( µ ,ν ) nazywamy tensor
( µ ,ν )
1
( µ ,ν )
TS
= (T + T T ) ,
2
zaś jego częścią antysymetryczną tensor
( µ ,ν )
1
( µ ,ν )
TA
= (T − T T ).
2
Z tych dwóch równości wynika, że
( µ ,ν )
( µ ,ν )
T = TS
+ TA .
(3.15)
(3.16)
(3.17)
Tensor T nazywamy tensorem symetrycznym po parze ( µ ,ν ) , gdy
zachodzi równość
( µ ,ν )
T
T
=T
(3.18)
i nazywamy go tensorem antysymetrycznym po tej parze, gdy
( µ ,ν )
T
T
= −T.
(3.19)
45
3.3. Tensory drugiego rzędu
Tensor symetryczny po każdej parze nazywamy tensorem absolutnie
symetrycznym. Tensor antysymetryczny po każdej parze nazywamy
tensorem absolutnie antysymeytrycznym.
Działania liniowe zachowują własności symetrii i antysymetrii.
Wynika stąd, że przestrzeń liniowa tensorów o tej samej walencji T p jest
sumą prostą (2.9) podprzestrzeni liniowych tensorów symetrycznych i
tensorów antysymetrycznych po parze ( µ ,ν )
T p = TS
( µ ,ν )
⊕TA
( µ ,ν )
.
Tensory drugiego rzędu (o walencji 2) są elementami przestrzeni
T 2 =∋ 3 ⊗ ∋ 3 utworzonej z iloczynu tensorowego dwóch przestrzeni
euklidesowych wektorowych. Odgrywają one zasadniczą rolę w
zastosowaniach.
Przestrzeń tensorów drugiego rzędu jest przestrzenią liniową. Takie
operacje wewnętrzne jak suma tensorów, jak również ich proste nasunięcie
nie wyprowadzają poza ten zbiór.
Jeżeli A, B ∈ T 2 , to A + B ∈ T 2 i AB ∈ T 2.
Tensory symetryczne są grupą ze względu na operację dodawania
(T 2 , + ) (2.1).
Dla tensora A
element neutralny grupy 0 − tensor zerowy,
element przeciwny grupy - A.
Tensory drugiego rzędu należące do T 2 nie są grupą ze względu na
operację prostego nasunięcia, ponieważ nie dla każdego tensora A ∈ T 2
istnieje tensor przeciwny A −1 = X taki, że
A X = X A = G = 1; 1 - element neutralny grupy, gdy istnieje A −1 .
46
Zbiór tensorów
1


N = A ∈ T 2 ; −1∨ A −1 A = A A −1 = 1
A ∈T 2


(3.20)
stanowi grupę tensorów nieosobliwych.
Jest to grupa ze względu na operację prostego nasunięcia. Jeśli
A ∈ T 2 i B ∈ T 2 , to A B ∈ T 2 . Tensorem neutralnym grupy jest tensor
jednostkowy 1, zaś tensorem przeciwnym jest tensor odwrotny A −1 = X .
Przestrzeń tensorów drugiego rzędu T 2 jest przestrzenią 9-cio
wymiarową. Przestrzeń macierzy kwadratowych M 2 jest również
przestrzenią 9-cio wymiarową. Przestrzenie te są izomorficzne, [30].
Ustalając w T 2 pewną polibazę ei ⊗ e j (3.3) możemy odnieść
wszystkie tensory do tej polibazy. Układ liczb Ai j taki, że A = Ai j ei ⊗ e j
jest uporządkowany przez dwa indeksy i może być utożsamiany z macierzą
kwadratową ( Ai j ).
Odwzorowanie A ⇔ Ai j jest izomorfizmem o własnościach:
( )
( ) ( )
A B ⇔ (A )(B ),
A ⇔ (A ) = (A ),
A ⇔ (A )(A ).
A + B ⇔ Ai j + B i j ,
i
T
2
i
i
j
j
j
k
T
i
j
(3.21)
j
j
k
Utworzony izomorfizm można wykorzystać do przeniesienia szeregu
faktów z teorii macierzy do teorii tensorów o walencji 2. Odwzorowanie
A ⇔ Ai j zależy od wyboru polibazy.
( )
TENSORY PODOBNE, MACIERZE PODOBNE
Dwie macierze ( Ai j ) i ( Aα β ) są podobne, jeżeli
47
(A ) = (g )(A )(g )
(g )(g ) = δ , gdzie g
i
α
i
j
i
i
α
α
α
β
β
β
j
β
hα i h β inna baza i kobaza w
i
α
g β j = hβ ⋅ e j ,
= e i ⋅ hα ,
∋3 .
Niezmienniczość względem relacji podobieństwa [41]
1 ⋅ A = tr (A ) ≡ Ai i = Aα α ,
det A =
[
]
(3.22)
1
3
2 tr (A A A ) − 3 tr (A A )tr A + (tr A ) = det Ai j = det Aα β .
6
( )
(
)
Potęga tensora drugiego rzędu jest zdefiniowana następująco:
2
A = AA
n −1
n
A= AA
n m
m
nm
n
 A = A.
 
n+m
AA = A
(3.23)
TWIERDZENIE 3.3
w
Odwzorowanie liniowe ∋3 
→
∋3 jest zadane przez zadanie afinora
A na dowolnej bazie ei w ∋3 . Wynika to z tzw. fundamentalnej
tożsamości dla dowolnego operatora L i dowolnej bazy [31].
Jeżeli ei i e j są bazą i kobazą w
∧
a ∈∋
3
Stąd wynika, że
∋3 , to
a = a i ei , gdzie a i = a ⋅ ei .
(
)
A ⋅ a = a i A ⋅ ei = A ⋅ ei ⊗ ei ⋅ a
i ostatecznie otrzymujemy afinor A w postaci
A = A ⋅ei ⊗ ei .
Gdy A = 1 wówczas
1 = 1 ⋅ ei ⊗ ei = ei ⊗ ei = e1 ⊗ e1 + e 2 ⊗ e 2 + e3 ⊗ e3 .
Dla bazy ortonormalnej (ei ⋅ e j = δ ij ) zachodzi równość
A = A ⋅ei ⊗ ei .
(3.24)
48
WARTOŚCI WŁASNE I WEKTORY WŁASNE
Dowolny wektor a o długości a i wersorze kierunkowym ν pod
wpływem afinora A jest odwzorowany w inny wektor b = Aa = aAT , który
różni się od a zarówno długością jak również kierunkiem. I tak, wektor a
doznaje wydłużenia λν
λν =
1
b
Aa a Aν
=
=
= Aν = ( νA T Aν ) 2
a
a
a
oraz zmienia swój kierunek
cos ϕ ≡ cos( ν, Aν ) =
ν ⋅ Aν νAν
=
.
ν Aν
λν
(3.25)
(3.26)
Wektor A (ν ) ≡ Aν nazywamy składową wektorową tensora A dla
kierunku ν , zaś skalar A(νν ) ≡ ν ⋅ Aν = νAν nazywamy składową normalną
tensora A dla kierunku ν . Jest to rzut wektora A (ν ) na kierunek ν . Jeżeli
wersor µ jest ortogonalny do ν (µ ⋅ ν = 0) , to rzut wektora A (ν ) na
kierunek µ - A(νµ ) = µAν = νAT µ nazywamy składową styczną tensora A
dla pary kierunków ( ν, µ). Na ogół
µAν ≠ νAµ .
Definicja
Każdy wektor a ≠ 0 spełniający równanie A ⋅ a = Aa, A ∈ R
nazywamy wektorem własnym tensora A odpowiadającym liczbie A; liczbę
A nazywamy wartością własną tensora A.
Wektor własny a pod wpływem afinora A nie zmienia swojej
orientacji. Z (3.26) wynika wówczas, że ϕ = 0 , cos ϕ = 1 i λν = νAν .
Z równości (A − A 1)a = 0 (równanie jednorodne) wynika, że jeżeli
mają istnieć niezerowe wektory a spełniające tę równość, to tensor
(A − A1) musi być osobliwy, ( det (A − A 1) = 0 ). Oznacza to, że zeruje się
wyznacznik macierzy
49
1
2
3
A1 − A
A1
A1
1
2
3
=0
A2
A2 − A
A2
1
2
3
A3
A3
A3 − A
(3.27)
Przyrównując do zera wyznacznik otrzymujemy równanie trzeciego
stopnia na wartość własną A . Wartości własne tensora A pokrywają się
zatem z pierwiastkami rzeczywistymi równania charakterystycznego
A3 − I A A2 − II A A − III A = 0 ,
(3.28)
gdzie (3.22)
1  2 

I A = tr (A ), II A =  tr  A  − (tr (A )) 2 , III A = det (A ).
2  

Z algebry liniowej wynika, że równanie trzeciego stopnia posiada co
najmniej jeden pierwiastek rzeczywisty, [23]. Rzeczywistym wartościom
własnym odpowiadają wówczas rzeczywiste wektory własne. Wyznaczamy
je z następującego układu równań jednorodnych
( A1 − A)ν 1 + A1 ν 2 + A1 ν 3 = 0,
1
2
3
A2 ν 1 + ( A2 − A)ν 2 + A2 ν 3 = 0,
1
2
3
A3 ν 1 + A3 ν 2 + ( A3 − A)ν 3 = 0,
1
2
3
gdzie przyjęto, że a = aν . Należy pamiętać, że ν = 1.
Z fundamentalnej tożsamości (3.24) wynika, że jeżeli
A e1 = A1 e1 , A e 2 = A2 e 2 , A e 3 = A3 e 3 ,
to otrzymujemy tensora A w postaci
A = A e i ⊗ e i = A1 e 1 ⊗ e 1 + A 2 e 2 ⊗ e 2 + A 3 e 3 ⊗ e 3 .
(3. 29)
Macierz reprezentacji tensora ma wówczas postać diagonalną, ponieważ
wektory bazy są wektorami własnymi dla tensora A .
Postać (3. 29) tensora A nazywamy jego rozkładem spektralnym.
50
Podprzestrzeń P ⊂ ∋ 3 nazywamy podprzestrzenią inwariantną tensora A ,
jeżeli
∧ Aa ∈ P .
a ∈P
Nie należy sądzić, że podprzestrzeń inwariantna składa się z wektorów
własnych. Podprzestrzeń P może nie zawierać żadnego wektora własnego.
Podprzestrzenią własną tensora A dla wartości własnej A nazywamy
zbiór rozwiązań równania
Aa = Aa ,
N A = {a ∈∋3 ; Aa = Aa} .
Jest to zbiór wektorów własnych tensora A odpowiadających wartości
własnej A uzupełniony wektorem własnym zerowym. Podprzestrzeń
własna tensora A jest podprzestrzenią inwariantną tensora A.
TWIERDZENIE 3.4
Wektory własne tensora A odpowiadające wartości własnej λ są
wektorami własnymi dowolnego wielomianu od A . Jeżeli
m
ϕ (A ) = α 0 1 + α 1 A + K + α m A ,
αν ∈ R
(3.30)
to odpowiadająca jemu wartość własna spełnia równość
m
ϕ (λ ) = α 0 1 + α 1 λ + K + α m λ .
Dla tensora nieosobliwego potęgi mogą być ujemne.
Dowód tego twierdzenia wynika z faktu, że wektor własny tensora jest
wektorem własnym dowolnej jego potęgi, a mianowicie
A na = A n−1Aa = AA n−1a = ....... = Ana .
(3.31)
51
Dla n=2 wzór (3.31) przyjmuje postać
A 2a = AAa = A( Aa) = AAa = A( Aa) = A2a .
Ponadto, wartość własna dla dowolnej potęgi tensora jest taką samą potęgą
wartości własnej tensora.
Z punktu widzenia potrzeb mechaniki ośrodków ciągłych interesują
nas tensory drugiego rzędu, które spełniają równość
A = AT ⇒ aAb = bAa .
(3.32)
Są to tensory symetryczne.
TWIERDZENIE 3.5
Dla każdego tensora symetrycznego drugiego rzędu równanie
charakterystyczne posiada trzy pierwiastki rzeczywiste. Wektory własne
odpowiadające różnym wartościom własnym są ortogonalne.
Symetria tensora jest warunkiem wystarczającym, ale nie koniecznym.
Mogą istnieć niesymetryczne tensory o rzeczywistych wartościach
własnych, n. p.
α 1 0 


(Aij ) =  0 α 1 .
0 0 α


Wielomian charakterystyczny tego tensora ( A − α ) = 0 ma potrójny
pierwiastek rzeczywisty A = α .
Jeżeli tensor A jest symetryczny i ma potrójny pierwiastek, wówczas
jest tensorem postaci A = α 1 , tzn.
3
1 0 0


(Aij ) = α  0 1 0 .
0 0 1


Takie tensory nazywamy tensorami kulistymi.
Każdy tensor symetryczny można przedstawić w postaci sumy tensora
kulistego P i dewiatora D (trD = 0)
52
A = P+D,
1
gdzie P = (trA)1 , ( trP = trA , ponieważ tr1 = 3 ) i D = A − P . Rozkład
3
ten jest jednoznaczny.
TWIERDZENIE 3.6
Twierdzenie Cayley’a-Hamiltona
Każdy tensor drugiego rzędu jest pierwiastkiem swego wielomianu
charakterystycznego
3
2
A = I A A + II A A + III A 1.
(3.33)
Dowód tego twierdzenia wynika z wielomianu charakterystycznego
(3.28) i z twierdzenia 3.4.
PROJEKTORY
Ważną i prostą klasę afinorów stanowią projektory.
Niech przestrzeń ∋3 = M ⊕ N jest sumą prostą dwóch podprzestrzeni M , N ,
wówczas
∧
a = a1 + a 2 ; a1 ∈ M , a 2 ∈ N .
a ∈∋3
Tensor P1 drugiego rzędu jest projektorem na M równoległym do N ,
jeżeli
P1 a = a 1 .
Jeżeli a ∈ M , to projektor działa jak operator tożsamościowy
P1 a = a. Dla a ∉ M P1 a = 0.
Postać projektora zależy od wymiaru podprzestrzeni M . Jeżeli M jest
podprzestrzenią jednowymiarową, to projektor ma postać
P1 = e 1 ⊗ e 1 .
(3.34)
Zachodzi wówczas następująca równość
(
) (
)
P1 a = e 1 ⊗ e 1 a = e 1 ⋅ a e 1 = a 1 e 1 = a 1 .
53
Dla podprzestrzeni M o wymiarze 2 wybieramy dowolną bazę w M , n. p.
e1 i e 2 . Wówczas
a1 = a1 e1 + a 2 e 2 , a 2 = a 3 e 3 ,
P1 e1 = e1 , P1 e 2 = e 2 , P1 e3 = 0.
Stąd wynika, że
(
) (
)
P1 = e 1 ⊗ e 1 + e 2 ⊗ e 2 .
(3.35)
Definicja
Projektor P1 nazywamy ortogonalnym, gdy M ⊥ N tzn.
∧
a ∈∋3
a 1 ⋅ a 2 = 0.
Każdy projektor można wówczas zapisać w postaci:
P = n1 ⊗ n 1 + n 2 ⊗ n 2 , n k ⋅ n l = δ kl
lub
P = n1 ⊗ n1 , n k − baza ortonormalna.
Każdy projektor ortogonalny jest symetryczny.
TWIERDZENIE 3.7
Twierdzenie o rozkładzie spektralnym (widmowym) tensora
symetrycznego drugiego rzędu, afinora A można sformułować w
następujący sposób.
Każdy tensor symetryczny A ∈ T 2S daje się przedstawić w postaci
kombinacji liniowej projektorów ortogonalnych, wzajemnie ortogonalnych
A = A1 P1 + K + Ar Pr , r ≤ 3.
Dla jednokrotnych wartości własnych przestrzenie wektorów
własnych są jednowymiarowe i wektory własne określone są z dokładnością
do znaku (r=3). Projektory ortogonalne są wówczas postaci:
54
P1 = ν I ⊗ ν I , A ν I = AI ν I ;
P2 = ν II ⊗ ν II , A ν II = AII ν II ;
P3 = ν III ⊗ ν III , Aν III = AIII ν III
i rozkład spektralny ma postać
A
=
T
1
µ
I
⊗
µ
I
+
T
II
µ
II
⊗
µ
II
+
T
III
µ
III
⊗
µ
III
.
A = AIν I ⊗ ν I + AII ν II ⊗ ν II + AIII ν III ⊗ ν III .
(3.36)
Dla podwójnej wartości własnej podprzestrzeń własna jest
dwuwymiarowa, ponieważ dla tensorów symetrycznych krotność
algebraiczna jest równa krotności geometrycznej.
Jeżeli AI = AII ≠ AIII wówczas
A = AI P1 + AII ν III ⊗ ν III ,
(3.37)
gdzie
P1 = ν I ⊗ ν I + ν II ⊗ ν II .
Wektory własne ν I i ν II stanowią wówczas dowolną bazę
ortonormalną w dwuwymiarowej podprzestrzeni własnej P1 .
Dla potrójnej wartości własnej, gdy AI = AII = AIII = A
A = A1, P1 = 1,
gdzie
P1 = ν I ⊗ ν I + ν II ⊗ ν II + ν III ⊗ ν III = µ I ⊗ µ I + µ II ⊗ µ II + µ III ⊗ µ III .
Dowolna baza ortonormalna jest bazą wektorów własnych.
Rozdział 4. Automorfizmy przestrzeni tensorowych
4.1. Tensory ortogonalne
Automorfizmami przestrzeni tensorowej T p nazywamy wszystkie
na
odwracalne przekształcenia linowe tej przestrzeni na siebie: T p 
→
Tp.
Przestrzeń T p jest przestrzenią otrzymaną z iloczynu tensorowego p
przestrzeni wektorowych
∋
3
p
T p = ⊗ ∋3 =∋3 ⊗ ∋3 ⊗K⊗ ∋3 .
1
na
→
T p musza zachować strukturę T p . Będą to
Automorfizmy T p 
zatem automorfizmy
na
∋3 →
∋3 .
generowane
przez
automorfizmy
przestrzeni
na
→
∋3 nazywamy afinory odwracalne, które
Automorfizmami ∋3 
zachowują strukturę przestrzeni euklidesowej wektorowej tzn. iloczyn
skalarny
(A ⋅ a ) ⋅ (A ⋅ b ) = a ⋅ b ⇒ A AT = 1.
(4.1)
Afinory o tej własności nazywamy afinorami ortogonalnymi. Będziemy je
oznaczać przez Q . Tensory ortogonalne
θ = {Q ∈ T 2 ; Q Q
T
= 1 } ; det Q = ±1,
(det (Q )) 2 = 1.
(4.2)
stanowią grupę ze względu na proste nasunięcie.
Tensory o własności det (A ) = ±1 nazywamy tensorami unimodularnymi
U = { Α ∈ T 2 ; det (Α ) = ±1 }; U ⊂ θ ⊂ N ⊂ T 2 .
TWIERDZENIE 4.1
Każdy tensor ortogonalny można przedstawić w postaci
Q = m1 ⊗ n1 + m 2 ⊗ n 2 + m 3 ⊗ n 3 .
(4.3)
56
Wynika to z fundamentalnej tożsamości (3.24) A = A ei ⊗ ei dla bazy
ortonormalnej n i (n i ⋅n j = δ ij ) i afinora Q
Q = Q ni ⊗ ni = mi ⊗ ni ,
gdzie Q n i = m i .
Każdy wektor a
a = a1n1 + a2n 2 + a3n 3
jest odwzorowany w wektor Q a o postaci
Q a = a1 Q n1 + a2 Q n 2 + a3 Q n 3 = a1m1 + a2m 2 + a3m 3 .
TWIERDZENIE 4.2
Dla każdego tensora Q ∈ θ (ortogonalnego) istnieje taka baza
ortonormalna n i i taki kąt ϕ , 0 ≤ ϕ ≤ 2π , że
Q = det(Q ){n1 ⊗ n1 + cosϕ (n2 ⊗ n2 + n3 ⊗ n3 ) + sinϕ (− n2 ⊗ n3 + n3 ⊗ n2 )}, (4.4)
0
1

Q ≅ det (Q ) 0 cosϕ
 0 sin ϕ



− sin ϕ  .
cos ϕ 
0
Gdy det (Q ) = 1 , to Q ∈R ( R – właściwa grupa ortogonalna lub grupa
obrotów)
R ≡ {Q ∈ T 2 ; Q Q
T
= 1, det (Q ) = 1 }.
(4.5)
TWIERDZENIE 4.3
Właściwą grupą ortogonalną R nazywamy podgrupę pełnej grupy
ortogonalnej θ składającą się z tensorów postaci
R ϕk = k ⊗ k + cos ϕ (l ⊗ l + n ⊗ n ) + sin ϕ (n ⊗ l − l ⊗ n ),
(4.6)
57
4.1. Tensory ortogonalne
gdzie k , l, n, – baza ortonormalna; k – wektor obrotu; ϕ – kąt obrotu; Rkϕ
- tensor obrotu. Wersor k jest określony z dokładnością do znaku ± 1 ; l, n
– dowolne wersory tworzące z k bazę ortonormalną prawoskrętną.
Podzbiór R k ⊂ R składający się z tensorów o tym samym wersorze k
stanowi podgrupę grupy R
R ϕk Rψk = R ϕk +ψ ,
−1
R ϕk = R −k ϕ .
2π
n
k
2⋅
2π
n
( n−1)2π
Niech n jest liczbą całkowitą. Podzbiór: 1, R , R k , R k n stanowi
podgrupę skończoną grupy R k . Jest to grupa cykliczna o generatorze
2π
R kn rzędu n, R kn ⊂ R k .
Tensory Q dla których det (Q ) = −1 nazywamy tensorami odbicia M.
Zbiór tensorów ortogonalnych M takich, że
M ≡ {Q ∈θ ; det (Q ) = −1}
(4.7)
nie tworzy podgrupy grupy θ . Mamy wówczas równość θ = R ∪ M (suma
zbiorów).
Oznaczmy przez I inwersję, tzn. odwzorowanie takie, że
I a = −a, I = −1 . Z ogólnej postaci tensora ortogonalnego wynika, że
tensor odbicia jest postaci:
M = I Rϕk .
Tensor I k zdefiniowany jako I k = I R πk definiuje odbicie lustrzane
względem płaszczyzny prostopadłej do k . Wektorowi a postaci
a = a1 k + a2 l + a3 n,
I k przyporządkowuje wektor
I k a = I R πk a = R πk (− a ) = R πk (− a1 k − a2 l − a3 n ) = − a1 k + a2 l + a3 n, (4.8)
ponieważ R πk l = −l, R πk n = −n. Tensor M = I Rϕk = I k R ϕk −π
jest
kompozycją obrotu wokół k o kąt ϕ − π i odbicia lustrzanego względem
58
płaszczyzny ortogonalnej do k. Łączny wynik nazywamy obrotem
lustrzanym wokół k o kąt ϕ .
W mechanice ośrodków ciągłych istotną rolę przy opisie deformacji ośrodka
odgrywa rozkład tensora drugiego rzędu nieosobliwego na tensor
ortogonalny i tensor symetryczny. Jest to rozkład biegunowy (polarny)
tensora
TWIERDZENIE 4.4
Każdy tensor drugiego rzędu A nieosobliwy (det A ≠ 0) można w
sposób jednoznaczny przedstawić w postaci
A = QU = VQ ,
(4.9)
gdzie tensory drugiego rzędu U i V są tensorami symetrycznymi
i dodatnio określonymi, zaś tensor Q jest tensorem ortogonalnym.
Z rozkładu (4.9) wynika, że
2
2
U = AT A ,
V = AAT .
(4.10)
Tensory te są dodatnio określone, ponieważ dla dowolnego α spełniony jest
warunek
αAT Aα = ( Aα ) ⋅ ( Aα ) ≥ 0 .
Tensor Q wyznaczamy z równania
−1
−1
Q = AU = VA .
(4.11)
Tensory U i V są tensorami wzajemnie obróconymi. Między nimi zachodzą
następujące zależności:
V = QUQT i U = QT AQ .
Jeżeli tensor A jest tensorem osobliwym, wówczas z równości
det A = ± det U = ± det V
wynika, że tensory U i V są również tensorami osobliwymi i tensor Q
(4.11) nie jest wyznaczony jednoznacznie.
59
4.2. Automorfizmy przestrzeni tensorowych
Tensor U jest tensorem symetrycznym, a zatem można go przedstawić
w postaci jego rozkładu spektralnego (3.36)
U = U I n I ⊗ n I + U II n II ⊗ n II + U III n III ⊗ n III .
Z rozkładu biegunowego (4.9) wynika wówczas, że
A = UI QnI ⊗nI +UIIQnII ⊗nII +UIIIQnIII ⊗nIII = UI mI ⊗nI +UIImII ⊗nII +UIIInIII ⊗nIII,
gdzie m K = Qn K .
Z twierdzenia o rozkładzie biegunowym korzystamy w mechanice
ośrodków ciągłych przy rozkładzie tensora gradientu deformacji F .
4.2. Automorfizmy przestrzeni tensorowych
Automorfizmy Q przestrzeni ∋3 , Q ∈ θ , gdzie θ jest pełną grupą
ortogonalną, generują automorfizmy przestrzeni tensorów o walencji
p – Tp.
p
Z faktu, że T p = ∋3 ⊗ ∋3 ⊗K⊗ ∋3 = ⊗ ∋3 , wynika, że reprezentacją
1442443 1
p
grupy θ w przestrzeni T p jest odwzorowanie
p
⊗ Q ≡ (Q ⊗ Q ⊗ K ⊗ Q ).
(4.12)
1
Automorfizm T p powinien zachowywać relację tensorów rozkładalnych.
TWIERDZENIE 4.5
Odwzorowanie liniowe przestrzeni T p
na siebie określone na
tensorach rozkładalnych jako odwzorowanie
p
⊗Q : c ⊗ K ⊗ a ⊗ K ⊗ d → Q c ⊗ K ⊗ Q a ⊗ K ⊗ Q d ,
1
gdzie Q jest afinorem ortogonalnym, jest automorfizmem T p .
60
A zatem
p
⊗Q ∗ (c ⊗ K ⊗ a ⊗ K ⊗ d ) = Q c ⊗ K ⊗ Q a ⊗ K ⊗ Q d.
(4.13)
1
p
Często opuszcza się przed Q wyrażenie ⊗ .
1
Dla tensorów nierozkładalnych, gdy T = T ij K k e i ⊗ e j ⊗ K ⊗ e k ,
tensor T po zastosowaniu automorfizmu przechodzi w nowy tensor B
postaci
p
*
*
*
B = ⊗Q ∗ T = T ijKk Q e i ⊗Q e j ⊗ K ⊗ Q e k = T ijKk e i ⊗ e j ⊗ K ⊗ e k , (4.14)
1
*
gdzie e i = Q e i nowa baza w ∋3 . Tensory T i B mają te same składowe
ale w innych (obróconych) polibazach.
Zbiór P p ⊂ T p nazywamy przestrzenią tensorową, jeżeli jest
podprzestrzenią liniową T p stateczną względem automorfizmów, tzn.
∧
A ∈P
p
⊗Q ∗ A ∈ P p ,
p 1
gdzie Q jest dowolnym automorfizmem
∋3 .
GRUPA AUTOMORFIZMÓW T p – ( grupa permutacji σp )
Definicja
Permutacją tensora T nazywamy odwzorowanie
na
σ :Tp 
→
Tp, p ≥ 2
określone dla tensorów rozkładalnych przepisem [30]
61
4.3. Grupy symetrii tensorów
σ × (a1 ⊗ a 2 ⊗ K ⊗ a p ) ≡ aσ (1) ⊗ aσ (2 ) ⊗ K ⊗ aσ ( p ) ,
(4.15)
gdzie dla permutacji σ przyjęto następujące oznaczenia: σ = i , k ,K , q
oznacza, że
σ (1) = i , σ (2) = k , K , σ ( p ) = q.
Przykład:
Permutacja σ = 2, 4, 3, 1 tensora c ⊗ a ⊗ b ⊗ d daje tensor
σ × (c ⊗ a ⊗ b ⊗ d ) = a ⊗ d ⊗ b ⊗ c.
Zbiór wszystkich permutacji T p na siebie jest grupą ze względu na
działanie kompozycji. Grupę tę oznaczamy przez σ p . Zawiera ona p!
permutacji.
Dla tensorów dowolnej postaci, gdy
permutacja T jest określona na polibazie
T = T ij Kk e i ⊗ e j ⊗ K ⊗ e k
σ × T = T ij Kk σ × (e i ⊗ e j ⊗ K ⊗ e k ) .
Kompozycję
permutacji
σi i σ µ
−1
(4.16)
oznaczamy
−1
przez
−1
σ iµ = σ i × σ µ × (K). Permutacja odwrotna σ ; σ σ = σ σ = e , gdzie e permutacja tożsamościowa.
Przykład:
σ i = 2, 1, 4, 3 , σ µ = 1, 3, 4, 2 , σ iµ = 2, 4, 3, 1 .
Transpozycję [i, j ] 1 ≤ i < j ≤ p nazywamy permutacją σ ∈ σ p taką,
że
σ (i ) = j , σ ( j ) = i , σ (k ) = k ; k ≠ i , k ≠ j.
Transpozycja jest szczególnym przypadkiem permutacji cyklicznej
62
σ = [i , j , k ,K , s ]
[i , j , k ,K , s] = [ j , k ,K , s , i] = [k ,K , s , i , j ] = K
Permutacja cykliczna rodzi cykliczną podgrupę grupy σ p .
Automorfizmy T p są generowane albo przez afinory ortogonalne
Q ∈θ ⊂ T 2 (4.12) albo przez permutacje σ ∈ σ p (4.15). W wyniku tych
na
odwzorowań T p 
→
T p dowolny tensor T ∈ T p jest odwzorowany w inny
tensor T* . Na ogół T ≠ T*.
GRUPA SYMETRII TENSORA WZGLĘDEM Q ∈θ
Tensor T w wyniku automorfizmu rodzonego przez Q przechodzi w
tensor
1 
T* =  ⊗Q  ∗ T.
(4.17)
p 
Na ogół dla Q ≠ 1
1
T* =  ⊗ Q  ∗ T ≠ T .
p 
(4.18)
Jeżeli dla danego tensora T ∈ T p istnieją takie Q ∈θ , że w (4.18)
zachodzi równość, to tensory Q stanowią podgrupę θT ⊂θ grupy θ (4.2).
Faktycznie
p 
1) Jeżeli  ⊗ Q  ∗ T = T , to
1 
 p −1 
 p −1   p
⊗
∗
=
Q
T
Q   ⊗ Q
1 
⊗


 1   1
   p −1
QQ
 ∗ T =  ⊗
  1

p 
∗
=
T
1  ∗ T = T,

⊗

1 
63
p

p

2) Jeżeli  ⊗ Q 1  ∗ T = T i  ⊗ Q 2  ∗ T = T , to
1
1




p
p

Q 1 Q 2  ∗ T =  ⊗ Q 2  ∗ T = T.
⊗
1

1

Definicja
Podgrupę θ T grupy θ określoną jako
p


θ T =  Q ∈ θ ;  ⊗ Q  ∗ T = T 
1
(4.19)




nazywamy grupą symetrii tensora T ∈ T p . Tensor T jest inwariantny
względem automorfizmów Q ∈θT . Grupa symetrii tensora θT nie jest pusta.
Tensor T nazywamy izotropowym, gdy θT =θ.
Tensor T nazywamy hemitropowym, gdy θT = R.
Jeżeli θT ≠ R , θT ≠ θ , to tensor T nazywamy anizotropowym.
Tensor T jest całkowicie anizotropowy, gdy
θ T = {1} dla p nieparzystego,
θ T = {1, − 1} dla p parzystego.
Definicja
Grupą symetrii zbioru tensorów a ∈∋ 3 , A ∈ T 2 ,K , T ∈ T p (o różnych
walencjach) nazywamy część wspólną grup symetrii wszystkich tensorów z
tego zbioru
θ a , A, K,T ≡ θ a ∩ θ A ∩ K ∩ θ T
(4.20)
Wnioski:
Tensory hemitropowe o walencji parzystej nie istnieją.
Tensory izotropowe o walencji nieparzystej nie istnieją.
Symetria tensora jest równoważna pewnym warunkom nałożonym na
jego reprezentację.
64
Definicja
Dwie bazy e i i hα nazywamy izometrycznymi względem podgrupy
~
~
θ ⊂ θ , jeżeli istnieje takie Q ∈θ , że e i = δ α i Q hα .
Polibazy e i ⊗ e j ⊗ K ⊗ e k i hα ⊗ h β ⊗ K ⊗ h γ są izometryczne
~
względem θ przy tym samym Q , jeżeli pary baz e i , hα ; e j , h β K są
izometryczne.
~
~
Podgrupa θ ⊂ θ jest grupą symetrii tensora T ∈ Tp θ = θ T wtedy
i tylko wtedy, gdy reprezentacje T w polibazach izometrycznych względem
~
θ są takie same.
Tensor T jest izotropowy wtedy i tylko wtedy, gdy jego reprezentacje
we wszystkich polibazach typu: n1 ⊗ n 2 ⊗ K ⊗ n k , ( n k – baza
ortonormalna) są takie same. Dwie dowolne bazy ortonormalne są
izometryczne względem θ.
(
)
GRUPA SYMETRII WEWNĘTRZNEJ TENSORA
Definicja
Grupą symetrii wewnętrznej tensora T ∈ T p nazywamy podgrupę
grupy σ p – automorfizmów zadanych przez permutacje
S T ≡ {σ ∈ σ p ; σ × T = T} .
(4.21)
Tensor T nazywamy absolutnie symetrycznym, gdy ST = σ p .
Gdy T ∈ T 2 jest tensorem drugiego rzędu (o walencji 2), to σ 2 – grupa
permutacji jest dwuelementowa
e = 1, 2 , σ = 2, 1 , T symetryczny gdy ST = σ 2 .
Dla tensorów 4 – tego rzędu T ∈ T 4 grupa σ 4 jest 4!= 24
elementowa.
65
4.4. Przykłady grup symetrii
Permutacje
1, 2, 3, 4 , 2, 1, 3, 4 , 1, 2, 4, 3 , 3, 4, 1, 2
generują podgrupę σ~ 4 . Tensory dla których ST = σ~ 4 mają duże
zastosowanie w mechanice. (Tensory Hookeà).
PEŁNA GRUPA SYMETRII TENSORÓW
Symetria tensora może być rozpatrywana względem automorfizmów
T p rodzonych przez θ – tensory ortogonalne – symetria zewnętrzna tensora
i względem automorfizmów rodzonych przez σ p – permutacje (4.21) –
symetria wewnętrzna tensora. Możemy połączyć te dwie grupy. Utwórzmy
z grup θ i σ p dla T p nieuporządkowane pary
(σ , Q ) = (Q , σ )
σ ∈ σ p , Q ∈θ ,
(4.22)
które tworzą grupę Σ .
Działaniem w grupie jest następujące działanie:
(σ~ , Q~ )× (σ( ,Q( )≡ (σ~σ( , Q~ Q( ).
Grupę Σ nazywamy iloczynem prostym grup θ , σ p i zapisujemy
w postaci
Σ = θ × σ p = σ p × θ (nie jest to iloczyn kartezjański!!!).
Definicja
Pełną grupą symetrii tensora T ∈ T p nazywamy podgrupę grupy Σ
o własnościach


 p  
(4.23)
Σ T = (σ , Q ) ∈ Σ; σ ×  ⊗ Q  ∗ T = T  .
 1  


Rozpatrzymy teraz jako przykłady grupy symetrii tensorów o różnych
walencjach (4.19).
1) Grupa symetrii wektora n
66
θ n = { Q ∈θ ; Q n = n
}.
Z faktu, że każdy tensor ortogonalny można przedstawić w postaci
(4.3):
Q = m1 ⊗ n 1 + m 2 ⊗ n 2 + m 3 ⊗ n 3 ,
wynika, że gdy n 1 = n Q n = n , to
Q = n ⊗ n + m2 ⊗ n 2 + m3 ⊗ n3 ,
gdzie Q n i = m i .
Stąd wynika, że
θ n = {1, Rϕn , I k } , k ⊥ n.
Jest to dowolny obrót wokół kierunku n oraz odbicie względem
płaszczyzny w której leży kierunek n (płaszczyzny prostopadłej do
kierunku k)
k ⊥ n.
2) Grupa symetrii pary liniowo niezależnych wersorów n, m (4.19)
θ n, m = { Q ∈θ ; Q n = n, Q m = m
Q (n + m ) = Q m + Q m = n + m.
}
Podprzestrzeń rozpięta na wektorach n i m jest podprzestrzenią
własną Q
Q = n ⊗ n + m ⊗ m ±Q l ⊗ l
n⊥m, l⊥n, l⊥m
θ n , m = { 1, I l }.
Jest to odbicie względem płaszczyzny prostopadłej do kierunku l.
3) Grupa symetrii trzech wersorów liniowo niezależnych n, m, l
θ n, m, l = { 1 }
.
4) Grupa symetrii diady n ⊗ n (4.19)
m, l ⊥ n
θ n⊗n = {Q ∈ θ ; Q n ⊗ Q n = Q n ⊗ n Q
Q n = ± n.
T
= n ⊗ n}
67
Stąd wynika, że
Grupa θ n⊗n
θ n ⊗n = {1, − 1, I n , I k , R ϕn }, k⊥n .
jest bogatsza od θ n o odbicie lustrzane I n .
5) Grupa symetrii diady n ⊗ m n ≠ m (4.19)
θ n⊗m = {Q ∈ θ ; Q n ⊗ Q m = n ⊗ m}
Q n ⊗ Q m = n ⊗ m.
Mnożąc lewostronnie przez n i prawostronnie przez m powyższe
wyrażenie otrzymujemy
(nQ n )Q m = m,
(m Q m )Q
n = n,
m, n − kierunki główne Q.
Stąd wynika, że
(nQ n)(mQ m)(Q m ⋅ Q n) = m ⋅ n,
(nQ n)(mQ m) = 1 ,
sign (nQ n ) = sign (mQ m) = ε = ±1 ,
ponieważ Q zachowuje iloczyn skalarny.
Wektory własne m, n odpowiadają tej samej wartości własnej ε .
Podprzestrzeń rozpięta na m, n jest podprzestrzenią własną; n 1 , n 2 – para
ortonormalna leżąca w tej płaszczyźnie
Q = ε ( n1 ⊗ n1 + n 2 ⊗ n 2 ) + ν n3 ⊗ n3 , n3 ⊥ n1 i n3 ⊥ n 2
θ n⊗m = θ n ⊗n = {1, − 1, I n } .
1
2
3
6) Grupa symetrii tensora drugiego rzędu A ∈ T 2
θ A = {Q ∈ θ ; Q A Q
T
= A }.
To znaczy, że Q A = AQ , AQ T = Q T A . Rozwiązań należy
poszukiwać tylko wśród tych Q , które przekształcają na siebie przestrzenie
własne A .
68
Gdy A ∈ T 2S (tensor symetryczny) wówczas z jego rozkładu
spektralnego (3.36)
A = A1 n 1 ⊗ n 1 + A2 n 2 ⊗ n 2 + A3 n 3 ⊗ n 3
wynika, że
a) gdy A1 ≠ A2 ≠ A3 ≠ A1
θ A = { 1, − 1, I 1 , I 2 , I 3 } .
Jest to grupa symetrii trzech diad n k ⊗ n k (4.19). Odbicia względem
płaszczyzn prostopadłych do trzech osi układu.
b) gdy A2 = A3 ≠ A1
θ A = {1, − 1, I n , R ϕn },
θA =θ.
c) gdy A1 = A2 = A3
1
1
Dwa tensory A, B ∈ T 2S będziemy nazywać zgodnymi, jeżeli istnieje
baza ortonormalna µ k taka, że
A = A1 µ1 ⊗ µ1 + A2 µ 2 ⊗ µ 2 + A3 µ 3 ⊗ µ 3
.
B = B1 µ1 ⊗ µ1 + B2 µ 2 ⊗ µ 2 + B3 µ 3 ⊗ µ 3
Niektóre z Ak mogą być sobie równe i tak samo dla Bk .
Dwa tensory A, B ∈ T 2S będziemy nazywać współosiowymi, gdy
przestrzenie własne tych tensorów pokrywają się. (Gdy wartości własne są
jednokrotne lub dla wartości wielokrotnych jeżeli A1 = A2 to B1 = B2 ).
Dwa tensory zgodne nie będące współosiowymi będziemy nazywać
częściowo współosiowymi, gdy wszystkie przestrzenie własne jednego
należą do przestrzeni własnych drugiego.
Wnioski:
1) Dwa tensory symetryczne A, B ∈ T 2S są zgodne ≡ θ A ∩ θ B = {1, − 1}.
2) Dwa tensory symetryczne A, B ∈ T 2S są współosiowe ≡ θ A = θ B .
3) Dwa tensory są częściowo współosiowe ≡ θ A ⊂ θ B lub θ B ⊂ θ A .
Rozdział 5. Tensory czwartego rzędu – liniowa teoria
sprężystości
5.1. Rozkład spektralny tensorów czwartego rzędu
Rozpatrujemy klasyczne ciało sprężyste, dla którego tensor małych
odkształceń ε związany jest z tensorem naprężeń Cauchy’ego σ liniowym
prawem Hooke’a [7], [17], [31], [32]
σ = S ⋅ ε , ε = C ⋅σ ,
(5.1)
σ ij = S ijmn ε mn , ε kl = C klmn σ mn ,
gdzie S jest tensorem sztywności, zaś C jest
Spełniona jest między nimi następująca zależność:
S
S o C = C o S = I S , C ijmn S mnkl = S ijmn C mnkl = I ijkl
;
tensorem podatności.
(I )
S
ijkl
=
1
(δ ik δ jl + δ il δ jk ).
2
Obszar stosowalności prawa Hooke’a określa warunek graniczny typu
Mises’a postaci ([21], [22])
σ H σ ≤ 1,
gdzie H jest tensorem granicznym.
Tensory S, C i H są tensorami czwartego rzędu. Są to elementy
przestrzeni T 4 , T 4 =∋3 ⊗ ∋3 ⊗ ∋3 ⊗ ∋3 , 34 − wymiarowej .
Posiadają one jednak pewne symetrie wewnętrzne (4.21) i zewnętrzne
(4.19), przy czym kolejność ich rozpatrywania jest dowolna.
Symetrie wewnętrzne są symetriami ze względu na permutacje dla
rozpatrywanych tensorów. Grupa symetrii (4.21) *σ 4 dla tensorów
czwartego rzędu typu Hooke’a jest postaci:
σ 1 = 1, 2, 3, 4 , σ 2 = 2, 1, 3, 4 , σ 3 = 1, 2, 4, 3 , σ 4 = 3, 4, 1, 2 *σ ⊂ σ .
4
4
70
Rozdział 5. Tensory czwartego rzędu – liniowa teoria sprężystości
Oznacza to, ze zachodzą następujące równości dla składowych tych
tensorów
Cijmn = C jimn = Cijnm = Cmnij ,
(5.2)
S mnkl = S nmkl = S mnlk = S klmn .
Tensory S, C i H są inwariantne względem *σ 4 . Fakt ten wynika z
symetrii tensorów odkształcenia i naprężenia oraz z istnienia potencjału.
Tensory S i C występują w prawie Hooke’a jako operatory liniowe
odwzorowujące T 2S → T 2S ; ( T 2S – przestrzeń tensorów symetrycznych
drugiego rzędu, tensory bezwymiarowe odkształcenia i tensory naprężenia
odniesione do naprężenia charakterystycznego). Tensor H będzie miał
charakter operatora liniowego, jeśli będziemy rozpatrywać stowarzyszone
prawo płynięcia. Tensor H występuje w formie kwadratowej. W formie
kwadratowej będą występowały również tensory S i C w wyrażeniu na
gęstość energii sprężystej [35], [36]
2 φ = ε ⋅ S ⋅ ε = σ ⋅ C ⋅ σ ≥ 0,
2φ = ε ij Sijkl ε kl = σ mn S mnklσ kl .
Poszukujemy ekstremum energii sprężystej na kuli
jednostkowej ε ⋅ ε = 1 ), (ekstremum warunkowe) wyrażenia (5.3)
ψ (ε ) = ε ⋅ S ⋅ ε − λ (ε ⋅ ε − 1),
∂ψ
= 2S ⋅ε − 2 λ ε = 0 ⇒ S ⋅ε = λ ε ,
ψε ≡
∂ε
(5.3)
(sferze
(5.4)
w ⋅ w = 1,
S ⋅ w = λ w ( λ − mnożnik Lagrange' a).
Warunek konieczny na istnienie ekstremum na kierunku w prowadzi
zatem do zagadnienia na stany własne [8], [35].
Dla deformacji ε w kierunku w
ε = e w,
e S ⋅ w = e λ w,
S ⋅ε = λ ε = σ .
71
Prawo Hooke’a na stanach własnych ma postać proporcjonalności
naprężenia i odkształcenia. Hooke w 1678 r. ogłosił swoje prawo w formie
„ut tensio sic vis” (ceiiinosssttuv). Stąd tytuł pracy [31].
Z teorii operatorów liniowych wynika, że równość (5.4)
S⋅w =λw
jest zagadnieniem na wartości własne i stany własne dla tensora S .
Unormowane rozwiązanie w (w - tensor symetryczny drugiego rzędu)
dla wartości λ nazywać będziemy sprężystym stanem własnym, zaś
skalar λ modułem sztywności. Pojęcie operatora liniowego, stanów
własnych i elementów własnych są pojęciami z algebry liniowej [8], [31],
[42].
Tensor S , jako operator występujący w prawie Hooke’a,
odwzorowuje przestrzeń tensorów symetrycznych drugiego rzędu T 2 S
w przestrzeń tensorów symetrycznych
S
S
S : T2 → T2 ,
T 2 = sym ∋ 3 ⊗ ∋ 3 .
S
Przestrzeń T 2 S jest przestrzenią liniową z iloczynem skalarnym
α ⋅ β = α ij β ij .
Wróćmy w tym miejscu do twierdzenia dotyczącego ogólnej postaci
liniowego odwzorowania przestrzeni tensorowych (3.13).
TWIERDZENIE 5.1
Niech L : P p → Pq jest
liniowym
odwzorowaniem
przestrzeni
tensorowej P p w przestrzeń tensorową Pq , gdzie p i q oznaczają walencje
tensorów, wówczas
1
∨
∧
L ∈T p + q A ∈P p
L (A ) = L ⋅ A = B∈Pq .
A zatem liniowe odwzorowanie przestrzeni tensorowych utożsamiamy
z tensorem o walencji p+q. Realizuje się ono przez pełne nasunięcie
tensorów L i A.
72
Przestrzeń P p jest przestrzenią liniową 3 p – wymiarową z iloczynem
skalarnym jako pełne nasunięcie dwóch tensorów A i B.
Normą tensora jest pełne nasunięcie tensora na siebie podniesione do
potęgi ½
1
2
A = (A ⋅ A ) .
W przestrzeni T p istnieje baza ortonormalna H k , (H k ⋅ H l = δ kl ) ,
która generuje całą przestrzeń T p , a mianowicie
1
∧
∨
A ∈ T p Ak ∈ R
A = Ak H k ,
Ak = A ⋅ H k .
Stąd wynika, że
L ⋅ A = Ak L ⋅ H k = (L ⋅ H k ⊗ H k ) A,
(5.5)
L = L ⋅ Hk ⊗ Hk .
W ogólnym przypadku w przestrzeni T p istnieje baza H k i kobaza
H l , takie, że H k ⋅ H l = δ k . Baza H k generuje całą przestrzeń T p
l
1
∧ ∨
A ∈Tp Ak ∈ R
A = Ak Hk , gdzie A ⋅ Hl = Ak Hk ⋅ Hl = A ⋅ Hl = Ak δ k = Al .
l
Otrzymujemy zatem, że
Ak = A ⋅ H k ,
L ⋅ A = L (Ak H k ) = Ak L ⋅ H k = (L ⋅ H k ⊗ H k ) ⋅ A.
Operator L jest określony jeśli jest on określony na bazie H k
L = L ⋅ Hk ⊗ Hk .
(5.6)
73
Równość ta jest fundamentalną tożsamością dla danego operatora
liniowego L i dowolnej bazy [31].
Z tej tożsamości wynika, że operator jest zadany, jeśli jest zadany na
tensorach bazy (można wprowadzić bazę ortonormalną (5.5)).
Jeśli operator L odwzorowuje T p → T p (p=q) wówczas L ∈ T 2 p i dla
takich operatorów ma sens zagadnienie na wartości własne i stany własne.
Gdy p =1 wówczas L ∈ T 2 i jest afinorem odwzorowującym ∋3 →∋3 ,
L = A.
Z fundamentalnej tożsamości wynika wówczas, że
A = Aµk ⊗ µk ,
gdzie µ k jest bazą ortonormalna w ∋3 .
Jeżeli µ k jest bazą wektorów własnych dla A wówczas otrzymujemy
rozkład spektralny tensora A (3.36)
A = A1 µ I ⊗ µ I + A2 µ II ⊗ µ II + A3 µ III ⊗ µ III .
Gdy p =2 operator L ∈ T 4 i odwzorowuje przestrzeń tensorów rzędu
drugiego w przestrzeń tensorów drugiego rzędu ( T 2 S → T 2 S ) . Takim
operatorem jest tensor sztywności S w prawie Hooke’a (5.1).
Z fundamentalnej tożsamości (5.6) dla przypadku, gdy L=S wynika,
że
S = S ⋅ νk ⊗ νk ,
gdzie ν k jest bazą ortonormalną w sześciowymiarowej przestrzeni
S
T 2 , ( k = I, II,..., VI).
Operatorem tożsamościowym jest tensor I – tensor jednostkowy
czwartego rzędu
I ⋅ A = A,
I = 1, 3, 2, 4 1 ⊗ 1,
(5.7)
I ijkm = δik δ jm .
T 2S
Przestrzeń
symetryczną I S
(I )
S
ijkm
(I )
S
ijkm
jest
symetryczna,
zatem
rozpatrujemy
1
(δik δ jm + δim δ jk ),
2
1
1
Akm = (δik δ jm + δim δ jk ) Akm = (Aij + A ji ).
2
2
=
część
74
Korzystając z fundamentalnej tożsamości (5.5) otrzymujemy, że
I S = I S ⋅ ν k ⊗ ν k = ν k ⊗ ν k = ν I ⊗ ν I + K + ν IV ⊗ ν IV + νV ⊗ νV + νVI ⊗ νVI .
Jest to rozkład spektralny I S , gdzie ν k
jest dowolną bazą
ortonormalną w T 2 S .
Z ogólnej teorii operatorów liniowych w przestrzeniach z iloczynem
skalarnym wynika, że dla operatorów o symetriach, które posiada S istnieje
sześć rzeczywistych wartości własnych λI ,KλVI , którym odpowiada sześć
określonych co do znaku wzajemnie ortogonalnych, unormowanych
tensorów własnych w I , K w VI .
Dla każdego k zachodzi wówczas równość
S ⋅ w k = λ k w k , k = I , II KVI (nie sumować ) .
Dla bazy w k , która jest bazą tensorów własnych, z fundamentalnej
tożsamości (5.5) dla operatora S wynika, że
S = S ⋅ w k ⊗ w k =λ I w I ⊗ w I + K +λ VI w VI ⊗ w VI .
(5.8)
Jest to rozkład spektralny tensora sztywności S [6], [31], [32], [35],
[42].
Dla tensora podatności zagadnienie na wartości własne ma wówczas
postać
1
C⋅wk =
wk .
λk
Oznacza to, że tensory sztywności i podatności maja takie samy stany
własne, zaś ich wartości własne są równe wzajemnej odwrotności. Rozkład
spektralny tensora podatności ma zatem postać
1
1
C = C⋅wk ⊗ wk =
w I ⊗ w I +K+
w VI ⊗ w VI .
(5.9)
λI
λ VI
Rozkłady spektralne (5.8) i (5.9) rozpatrywanych tensorów są wyznaczone
jednoznacznie, gdy wszystkie wartości λk są jednokrotne.
75
5.2. Projektory, moduły Kelvina
Wykorzystując rozkład spektralny tensora S (5.8), energię sprężystą
można wyrazić przez jego wartości własne. Z rozkładu spektralnego S oraz
rozkładu ε w bazie w k , a mianowicie
ε = eI w I + K + eVI wVI , ε ⋅ w k = ek
wynika, że
S ⋅ ε = (λI w I ⊗ w I + K + λVI wVI ⊗ wVI ) ⋅ ε = λI eI w I + K + λVI eVI wVI .
Stąd otrzymujemy wyrażenie na energię sprężystą w postaci
2φ = ε ⋅ S ⋅ ε = (λI eI w I + K + λVI eVI wVI ) ⋅ ε = λI e I2 + K + λVI eVI2 . (5.10)
Energię sprężystą w takiej postaci, bez wprowadzenia pojęcia stanów
własnych, podał Lord Kelvin (W. Thomson w 1856 r.) [44]. Z tego względu
Rychlewski [35] zaproponował aby moduły sztywności λk nazywać
modułami Kelvina. Każdy ciąg (λ I , K λVI ; w I , K w VI ) , gdzie λk są stałymi
nieujemnymi, a wersory w k , określone z dokładnością do znaku ± w k , są
bazą ortonormalną w T 2 S , opisuje pewien teoretycznie możliwy materiał
sprężysty.
Przestrzeń inwariantna dla operatora S
Podprzestrzeń M S ⊂ T 2 S nazywamy inwariantną dla S jeżeli
∧
A ∈M S
S ⋅ A ∈ MS .
Podprzestrzeń M S może nie zawierać żadnego tensora własnego.
Podprzestrzenie własne
Zbiór N λ rozwiązań równania S ⋅ A = λ A jest zbiorem tensorów
własnych dla operatora S odpowiadających wartości własnej λ
uzupełniony wektorem zerowym jest podprzestrzenią inwariantną dla S .
Nazywać ją będziemy podprzestrzenią własną
76
{
N λ = A ∈ T2 ; S ⋅ A = λ A } .
S
(5.11)
Nie każda podprzestrzeń inwariantna dla operatora S jest
podprzestrzenią własną. Podprzestrzenie własne odpowiadające różnym
wartościom λk są ortogonalne. Podprzestrzenie własne są przestrzeniami
inwariantnymi.
Istotną rolę w teorii odwzorowań liniowych odgrywają projektory
ortogonalne. Są to tensory czwartego rzędu – najprostsze , po operatorze
tożsamościowym (5.7), operatory liniowe. Poszukamy ich tensorowej
postaci.
Przedstawimy przestrzeń T 2 S w postaci sumy prostej podprzestrzeni
ortogonalnych
T 2 S = P1 ⊕ K ⊕ P6 .
(5.12)
S
Dowolny tensor A ∈ T 2 można wówczas przedstawić jednoznacznie
w postaci
A = A1 + A 2 + K + A 6 , A k ∈P k .
Tensor A k ∈ P k jest częścią tensora A. Istnieje tensor czwartego rzędu
Pk , który realizuje to przyporządkowanie
Pk ⋅ A = A k .
(5.13)
Tensor o tej własności nazywamy ortogonalnym projektorem T 2 S na
podprzestrzeń Pk . Jest to tensor, który na elementach A ∈ P k działa jak
tensor jednostkowy (operator tożsamościowy), zaś elementom nie
należącym do Pk przyporządkowuje tensory zerowe
A dla A ∈ P k ,
Pk ⋅ A = 
0 dla A ∉ P k .
Jest to tensor izotropowy.
będzie projektorem
Niech Pk
Pk odpowiadającą wartości własnej λk .
na
podprzestrzeń
własną
77
Z fundamentalnej tożsamości (5.5)
L = L⋅wk ⊗wk
wynika, że projektor Pk ma postać
Pk = Pk ⋅ w I ⊗ w I + K + Pk ⋅ w VI ⊗ w VI .
Z definicji projektora Pk otrzymujemy, że
Pk = w k ⊗ w k , (nie sumować)
P1 = w I ⊗ w I , P2 = w II ⊗ w II , K , P6 = w VI ⊗ w VI .
Dla operatora tożsamościowego (5.7) zachodzi zatem równość
I S = P1 + P2 + K + P6 .
(5.14)
Rozpatrywaliśmy dotychczas sytuację, gdy przestrzenie własne Pk
były jednowymiarowe ( λk ≠ λl dla k ≠ l ) .
Niech λk będzie l – krotnym pierwiastkiem (l – krotną wartością
własną tensora S ). Dla operatorów o symetrii tensora S wynika, że
krotność algebraiczna pokrywa się z krotnością geometryczną. Przestrzeń
własna Pk odpowiadająca wartości własnej λk jest również l – wymiarowa.
Niech w I , w II , K , w l będą dowolną bazą w Pk . Z fundamentalnej
tożsamości dla projektora (5.5)
Pk = Pk ⋅ w I ⊗ w I + K + Pk ⋅ w l ⊗ w l + Pk ⋅ w I +1 ⊗ w I +1 + Pk ⋅ w VI ⊗ w VI
oraz z faktu, że
Pk ⋅ w I = w I ,......, Pk ⋅ w l = w l ,
Pk ⋅ w l +1 = 0, Pk ⋅ wVI = 0
wynika postać projektora Pk , a mianowicie
Pk = w I ⊗ w I + K + w l ⊗ w l ,
(5.15)
78
Projektor Pk określony jest jednoznacznie. Należy podkreślić, że
poszczególne diady w k ⊗ w k nie są określone jednoznacznie.
Rozkład I S dla wielokrotnych modułów sztywności przyjmuje postać
I S = P1 + P2 + K + Pρ , ρ ≤ 6,
(5.16)
( ρ – liczba różnych modułów Kelvina).
Możemy zatem podać główny wzór strukturalny liniowej teorii
sprężystości.
TWIERDZENIE 5.2
Dla dowolnego sprężystego ciała S istnieje dokładnie jedno
ortogonalne rozłożenie przestrzeni tensorów symetrycznych drugiego rzędu
na podprzestrzenie Pk
T 2 S = P1 ⊕ P2 ⊕ K ⊕ Pρ , ρ ≤ 6, Pα ⊥ Pβ
i dokładnie jeden ciąg modułów Kelvina λ1 < λ2 < K < λρ taki, że
S = λ1 P1 + K + λ ρ Pρ ,
(5.17)
gdzie tensor Pk jest projektorem ortogonalnym na podprzestrzeń Pk .
Rozkład ten jest jednoznaczny ([6], [32], [35], [36], [42]).
Dla tensora podatności C rozkład spektralny (5.9) będzie miał
wówczas postać
1
1
(5.18)
C=
P1 + K +
Pρ .
λ1
λρ
Podprzestrzeń Pk tworzą wszystkie stany własne dla S
odpowiadające wartości własnej λk . Jeżeli S i C są zadane, to moduły λk
i projektory Pk wyznacza się w standartowy sposób. Projektory Pk
nazywane są projektorami materialnymi, a podprzestrzenie Pk
podprzestrzeniami materialnymi.
79
WYZNACZANIE MODUŁÓW KELVINA
Zagadnienie na wartości własne i stany własne dla operatora S (5.4)
sprowadza się do równości
S⋅w = λ w
(S − λ I ) ⋅ w = 0.
S
(5.19)
Jest to układ równań liniowych jednorodnych. Aby istniały niezerowe
rozwiązania, tensor S − λ 1 S musi być osobliwy, tzn. det S − λ 1 S = 0.
Powstaje pytanie: Jak policzyć wyznacznik dla tensora czwartego rzędu?
(
)
(
)
W przestrzeni T 2 S (sześciowymiarowej) wybieramy dowolną bazę
ortonormalną
ν K , K = I , II ,K , VI ;
ν K ⋅ ν L = δ KL .
Dla tensora L ∈ T4 det (L ) ≡ det (LKL ) , gdzie
L KL = ν K ⋅ L ⋅ ν L = L LK .
(5.20)
Macierz LKL jest macierzą kwadratową, symetryczną 6 µ 6 otrzymaną
z tensora L i dowolnej bazy ν K .
Stąd wynika, że
[
]
det (S − λ I S ) = det ν K ⋅ S ⋅ ν L − λ ν K ⋅ I S ⋅ ν L = det [ν K ⋅ S ⋅ ν L − λ δKL ].
Warunek
det (S − λ I S ) = 0
sprowadza
charakterystycznego 6 – tego stopnia dla λ
się
do
λ6 + a1 λ5 + a2 λ4 + K + a5 λ + a6 = 0.
równania
(5.21)
Współczynniki ak tego równania są funkcjami od niezmienników
tensora S i tym samym nie zależą od wyboru bazy [45].
Gdy ν k = w k , gdzie w k są stanami własnymi, macierz S KL
80
S KL = w K ⋅ S ⋅ w L
jest macierzą diagonalną.
Należy zwrócić uwagę na fakt, że tensory w k i − w k są fizycznie
różnymi tensorami. Nie istnieje takie Q , które odwzorowuje w → − w.
Teorie uwzględniające znak są teoriami silnie nieliniowymi.
Współczynniki występujące w równaniu charakterystycznym można
wyrazić przez moduły Kelvina.
Z równania
det (w K ⋅ S ⋅ w L − λ δ KL ) = 0
w bazie stanów własnych wynika, że
0
 λI − λ

λII − λ
 0
det 
M
M

 0
0



L
0 
= (λ − λI )(λ − λII )K (λ − λVI ) = 0.
O
M 

L λVI − λ 
L
0
Po uporządkowaniu wyrażeń przy odpowiednich potęgach λ
wyrażone przez λI , λII ,K , λVI .
otrzymujemy współczynniki ak
Współczynniki w równaniu charakterystycznym są niezmiennikami dla
tensora S. I tak np.
a 6 = det (S ) = λ I , K , λVI .
WYZNACZANIE PROJEKTORÓW
Jeżeli równanie charakterystyczne (5.21) ma ρ różnych
pierwiastków, to rozkład spektralny dla tensora S ma postać (5.17)
λk
S = λI P1 + K + λρ Pρ .
Każde z λk spełnia równanie charakterystyczne (5.21), mamy zatem ρ
równań
81
λ6I + a1 λ5I + K + a6 = 0,
λ6II + a1 λ5II + K + a6 = 0,
M
λ6ρ + a1 λ5ρ + K + a6 = 0.
Mnożąc odpowiednio pierwsze równanie przez P1 , drugie przez P2 …, ρ
przez Pρ i dodając stronami otrzymujemy równanie tensorowe
(λ P + λ
6
I
1
6
II
)
(
)
P2 + K + λ6ρ Pρ + a1 λ5I P1 + λ5II P2 + K + λ5ρ Pρ + K + a6 (P1 + P2 + K + Pρ ) = 0,
które ma postać uogólnionego równania Cayle’a-Hamilton’a (3.33)
6
5
S+ a1 S + K + a5 S + a6 1S = 0,
ponieważ z (5.17) wynika, że
n
S = λnI P1 + λnII P2 K + λnρ Pρ .
Aby wyznaczyć projektory P1 , P2 ,K, Pρ należy rozwiązać tensorowy
układ ρ równań liniowych :
P1 + P2 + K + Pρ = I S ,
λ I P1 + K + λ ρ Pρ = S,
M
( ρ −1)
( ρ −1)
( ρ −1)
( ρ −1)
λ I P1 + λ II P2 + K + λ ρ Pρ = S .
Wyznacznik podstawowy jest postaci wyznacznika Vandermonda
82
1
λI
2
∆ = λI
L L L
M
L L L
L L L
M M M
λI
L L L
( ρ −1)
1
λρ
λ2ρ =
M
Π (λα − λβ ).
1≤ β <α ≤ ρ
( ρ −1)
λρ
Z założenia λα ≠ λβ dla α ≠ β a zatem ∆ ≠ 0 . Stąd wynika, że
(S − λ 1 )o K o (S − λ
=
Pα
)(
)
(
)
1S o S − λα +1 1S o K o S − λρ 1S
,
(λα − λI )K(λα − λα −1 )(λα − λα +1 )K(λα − λρ )
S
I
α −1
λα = S ⋅ Pα .
Jeżeli dla danego materiału, dla danego S istnieje ρ parami różnych
modułów Kelvina λk ≠ λl gdy k ≠ l , to odpowiada im ρ podprzestrzeni
własnych wzajemnie ortogonalnych. Oznaczając przez qk wymiar
podprzestrzeni własnej Pk odpowiadającej λk otrzymujemy równość
q1 + q2 + K + qρ = 6.
Wyrażenie
q1 + q2 + K + qρ
(5.22)
Rychlewski [31] zaproponował nazwać
pierwszym indeksem strukturalnym. Jeżeli wielomian charakterystyczny
ma 6 różnych jednokrotnych pierwiastków, wówczas wszystkie przestrzenie
własne są jednowymiarowe i pierwszy indeks strukturalny ma postać
1+1+1+1+1+1 .
Z rozkładu spektralnego wynika, że jeśli są znane moduły Kelvina
λ1 ,K , λρ , to znany jest tensor sztywności S jeżeli zadane są projektory
PI ,K, Pρ . Projektory PI ,K, Pρ są tensorami rzędu czwartego. Nie znana
jest baza zupełna niezmienników dla takich tensorów [31], [45].
Dla jednokrotnych modułów Kelvina λk projektor Pk ma postać diady
stanów własnych
83
Pk = w k ⊗ w k (nie sumować),
a zatem ciąg (λI ,KλVI ; w I ,K, wVI ) dla w k określonych z dokładnością do
znaku ± w k opisuje pewien teoretycznie możliwy materiał S (5.8).
Tensory w k są symetryczne, unormowane w K ⋅ w L = 1 i ortogonalne
w K ⋅ w L = δ KL .
Tensor symetryczny drugiego rzędu w dowolnej bazie ma 6
składowych istotnie różnych. Dla 6 tensorów mamy 6 × 6 = 36 składowych.
6
Warunki ortonormalności stanowią   = 15 warunków + 6 warunków
 2
unormowania. Razem mamy 15 + 6 = 21 warunków. Pozostało zatem
36 − 21 = 15 wielkości niezależnych.
Tensor sztywności S ze względu na symetrię wewnętrzną ((4.21) ze
względu na permutacje) ma istotnie różnych 21 składowych. Wśród Sijkl
(3
)
= 81 istotnie różnych jest 21.
Rozmaitość ciał sprężystych jest opisana lokalnie w sposób ciągły przez
6 + 15 = 21 parametrów tworzących trzy grupy :
4
I. 6 modułów Kelvina – niezmienników, wielkości wymiarowych
mających wymiar naprężenia,
II. Z 15 wielkości wydzielamy 12 wielkości bezwymiarowych
związanych z w K , niezmienników zwanych dystrybutorami
sztywności, które oznaczamy przez κk .
III. 3 wielkości, które są związane z umiejscowieniem próbki
w laboratorium np. : kąty Eulera. Nie są to niezmienniki.
Możemy zatem napisać 6 + (12 + 3) = 21 .
Sprawa dystrybutorów jest sprawą złożoną, ponieważ dystrybutory
mają nie reagować na znak ± w k . Powstaje pytanie: Jak zadać te
dystrybutory aby otrzymać jednoznacznie określony materiał sprężysty S ?
Sprawę tę dla każdej symetrii materiału należy rozpatrywać niezależnie.
Jeżeli materiał posiada jakąkolwiek symetrię wówczas liczba
niezależnych składowych tensora S maleje. Pojawiają się wielokrotne
moduły Kelvina, wielowymiarowe przestrzenie własne. Maleje zatem liczba
dystrybutorów jak również liczba kątów Eulera.
84
W wyrażeniu
λI ,L, λVI ; κ1 ,L, κ12 ; ϕ1 , ϕ 2 , ϕ 3
należy napisać
λI ,L, λρ ; κ1 ,L, κ t ; ϕ1 , L, ϕ u .
Wyrażenie [ρ + t + u ] Rychlewski [31]
strukturalnym. Spełnione są nierówności
ρ ≤ 6, t ≤ 12, u ≤ 3;
nazwał
ρ + t + u ≤ 21 .
(5.23)
drugim
indeksem
(5.24)
Dalsza dyskusja materiałów sprężystych jest możliwa jeżeli nałoży się
pewne warunki symetrii na S (symetrii ze względu na automorfizm
rodzony przez tensory ortogonalne Q ∈θ ) (4.19).
Reasumując, możemy teraz odpowiedzieć na pytanie postawione przez
prof. Rychlewskiego w Instytucie Mechaniki w Moskwie, gdzie wygłosił w
1983 r. referat na seminarium : „O prawie Hooke’a” [31]. Pytanie to
brzmiało: „Co jeszcze można dopowiedzieć do prawa Hooke’a, po
klasycznych pracach Neumanna i Voighta?”. Odpowiedź brzmi, że można.
Załóżmy, że w dwóch różnych laboratoriach badano dwie próbki
i otrzymano zbiór danych: Sijkl i Si'' j' k' l . Składowe Sijkl , przy przypadkowym
ustawieniu próbki nie stanowią stałych materiałowych. Przy zmianie bazy
zmieniają się składowe. Czy badane próbki opisane przez Sijkl i Si'' j ' k ' l ' są z
tego samego materiału? Odpowiedzi ogólnej nie znamy. Nie znamy
kompletu stałych materiałowych, tzn. kompletu niezmienników opisujących
tensor S z dokładnością do sztywnego obrotu [45].
Jeżeli usytuowanie próbki względem laboratorium określają 3 kąty
Eulera, to funkcjonalnie zupełna baza niezmienników ortogonalnych,
opisujących lokalnie w sposób ciągły rozmaitość różnych od siebie
materiałów powinna zawierać 21 − 3 = 18 niezmienników.
Konwencjonalne podejście nie określa postaci takiej bazy dla materiału
postaci ogólnej. Klasyczna klasyfikacja tensorów sztywności według
symetrii wnosi tym mniej informacji im węższa jest grupa symetrii i nie
daje nic wówczas gdy rozważany materiał symetrii nie posiada. Należy się
spodziewać, że liczba materiałów o sterowanej symetrii będzie narastać.
85
Moduły sztywności i dystrybutory stanów własnych są jednakowe dla
dowolnych dwóch ciał z tego samego materiału.
Zawierają one w sobie całą informację o makrostrukturze ciała, która
jest wystarczająca do opisu jego sprężystego zachowania.
Przykład bazy w T 2 S generowanej przez bazę e k w ∋ 3 (ek ⋅ el = δkl ) :
ν I = e1 ⊗ e1 ,
ν II = e 2 ⊗ e 2 ,
ν III = e 3 ⊗ e 3
1
(e 2 ⊗ e 3 + e 3 ⊗ e 2 ),
2
1
(e1 ⊗ e 3 + e 3 ⊗ e1 ),
νV =
2
1
(e 2 ⊗ e1 + e1 ⊗ e 2 ).
νVI =
2
ν IV =
Jest to baza (polibaza) ortonormalna w T 2 S .
Jeżeli Sijkl , składowe tensora S w polibazie e i ⊗ e j ⊗ e k ⊗ e l tzn.
S = Sijkl ei ⊗ e j ⊗ e k ⊗ el ,
to macierz S KL = ν K ⋅ S ⋅ ν L będzie miała postać :
S1111

S2211
S
 3311




S1122
S1133
2 S1123
2 S1113
S2222
S3322
S2233
S3333
2 S2223
2 S3323
2S2323
2 S2213
2 S3313
2S2313
symetryczna
2S1313
2 S1112 

2 S2212 
2 S3312 
.
2S2312 
2S1312 

2S1212 
(5.25)
W fizyce kryształów jest popularna macierzowa forma opisywania prawa
Hooke’a [39]
86
MODUŁY SZTYWNOŚCI
Z twierdzenia spektralnego dla tensora podatności C (5.9)
1
1
1
C = wI ⊗ wI +
w II ⊗ w II + K +
wVI ⊗ wVI
λI
λII
λVI
wynika, że [31]:
a)
(tr w I )2 + (tr w II )2 + K + (tr wVI )2 ,
1
= 1⋅ C ⋅1 =
K
λI
λII
λVI
(5.26)
gdzie K jest modułem sztywności objętościowej.
b) Jeżeli n jest kierunkiem w
∋3 , to
(n ⋅ w I ⋅ n) + (n ⋅ w II ⋅ n) + K + (n ⋅ wVI ⋅ n) =
1
= n ⊗n ⋅C⋅n ⊗n =
E (n)
λI
λII
λVI
2
2
2
2
2
2
 ( nn) 
 ( nn)   ( nn) 
 wVI 
 w I   w II 
 ,




+K+ 
+
=
λI
λII
λVI
gdzie E (n ) jest modułem Young’a dla kierunku n.
c) Jeżeli n i m są dwoma kierunkami ortogonalnymi w
ν(m, n)
−
E(n)
= m⊗m⋅ C⋅ n⊗n =
(nn) (mm)
=
wI wI
λI
∋
3
, to
(n⋅wI ⋅ n)(m⋅wI ⋅ m) +K+ (n⋅wVI ⋅n)(m⋅wVI ⋅ m) =
λI
(nn) (mm)
+K+
(5.27)
wVI wVI
λVI
λVI
(5.28)
,
gdzie ν jest współczynnikiem Poissona w kierunku m przy rozciąganiu
w kierunku n .
87
5.3. Tensor stanu granicznego-energetyczne stany własne
d)
1
(n ⋅ w I ⋅ m) + (n ⋅ w II ⋅ m) + K + (n ⋅ wVI ⋅ m) =
= m ⊗n⋅C ⋅m ⊗n =
4G
λI
λII
λVI
2
2
2
2
2
 ( nm) 
 ( nm)   ( nm) 
 wVI 
 w I   w II 
 ,
=   +   +K+ 
λI
λII
2
(5.29)
λVI
gdzie G jest modułem ścinania (modułem Kirchhoffa).
Wnioski:
Do modułu sztywności objętościowej (5.26) nie wchodzą stany własne
dla których trw = 0 , stany dewiatorowe.
Do modułu Young’a E (n ) (5.27) nie wchodzą stany własne, dla
n
których składowa normalna dla kierunku
jest zerowa
( nn )


 w K = n ⋅ w K ⋅ n = 0 .


Do modułu Poissona (5.28) nie wchodzą stany własne dla których albo
( nn )
 ( mm)

m ⋅ w k ⋅m = 0 albo n ⋅ w k ⋅ n = 0  w K = 0, w K = 0  .


Do modułu ścinania (5.29) nie wchodzą stany własne, dla których
m ⋅ w k ⋅n = 0 (składowe styczne dla stanów własnych, dla pary kierunków
m, n są zerowe ).
5.3. Tensor stanu granicznego - energetyczne stany własne
Prawo Hooke’a (5.1), które było tematem poprzednich rozważań,
opisywało zachowanie sprężyste ciała w otoczeniu stanu naturalnego, tzn.
stanu bez naprężeń i odkształceń. Przy założeniu małych odkształceń można
było przyjąć, że zależność naprężenie - odkształcenie jest liniowa.
Sprężystość objawia się w odwracalności tego prawa.
Granicę stosowalności prawa Hooke’a określa warunek stanu
granicznego.
88
Kwadratowy warunek stanu granicznego
σ ⋅ H ⋅σ ≤ 1
(5.30)
jest uogólnieniem warunku granicznego zaproponowanego przez Mises’a
[22] w postaci
s ⋅ H ⋅ s ≤ 1,
gdzie s jest dewiatorem tensora naprężenia σ , zaś tensor H jest tensorem
czwartego rzędu zwany tensorem stanu granicznego
σ = s + σ 1; 3σ = tr (σ ).
Jeżeli σ * będzie stanem bezpiecznym, to
σ * ⋅ H ⋅ σ * = 0.
(5.31)
Stąd wynika, że H ⋅ σ * = 0 i σ * należy do jądra operatora H..
Warunek Mises’a s ⋅ H ⋅ s ≤ 1 jest warunkiem jaki otrzymujemy z
ogólnej postaci (5.30) przy założeniu, że stan hydrostatyczny σ = σ 1 jest
stanem bezpiecznym (5.31)
σ * = σ 1 ⇒ H ⋅ 1 = 0.
Otrzymujemy wówczas, że
σ ⋅ H ⋅ σ = (s + 1σ ) ⋅ H ⋅ (s + σ 1) = s ⋅ H ⋅ s , gdy H ⋅ 1 = 0.
Przyjęcie stanu hydrostatycznego za stan bezpieczny jest
przeniesieniem założenia z ciał izotropowych na ciała anizotropowe.
Założenie to nie ma żadnego fizycznego uzasadnienia w przypadku ciał
anizotropowych. Będziemy zatem rozważać warunek stanu granicznego w
postaci
σ ⋅ H ⋅σ ≤ 1
⇒ H ijkl σ ijσ kl ≤ 1,
89
przy założeniu, że H ma te same symetrie co S i C ze względu na
permutacje, oraz że
σ ⋅ H ⋅ σ ≥ 0.
Stany bezpieczne będą zależały od przyjętego typu symetrii
zewnętrznej H (symetrii ze względu na automorfizmy Q ∈θ ) (4.19).
Poszukując ekstremum wyrażenia σ ⋅ H ⋅ σ na sferze jednostkowej
σ ⋅σ = 1 otrzymujemy warunek konieczny na istnienie ekstremum w
postaci [35]
∂
∂σ


1
 σ ⋅ H ⋅ σ − 2 (σ ⋅ σ − 1) = 0.
χ


Stąd wynika, że
H ⋅σ =
1
χ2
σ.
(5.32)
Otrzymaliśmy zatem zagadnienie na wartości własne i stany własne dla
tensora H.
Z algebry liniowej, teorii operatorów biliniowych wynika, że tensor H
o założonych symetriach wewnętrznych jako operator liniowy ma sześć
rzeczywistych wartości własnych, którym odpowiada sześć rzeczywistych
stanów własnych κ k .
Przenosząc na tensor H wszystkie fakty dotyczące tensora sztywności
(5.17), przez analogię możemy napisać rozkład spektralny tensora H, a
mianowicie
H=
1
χ
2
1
R1 + K +
1
χ m2
R m , m ≤ 6,
(5.33)
R1 ,K, R m są tensorami czwartego rzędu, projektorami
gdzie
ortogonalnymi na podprzestrzenie własne R 1 ,K , R m . Spełniają one
równość
IS = R1 + K + R m .
90
Jeżeli R k jest podprzestrzenią własną, na którą projektor R k rzutuje σ , to
T 2S = R 1 ⊕ R 2 ⊕ K ⊕ R m
(suma prosta).
Wielkości χ1 , χ 2 ,K, χ m są granicznymi wartościami zakresu sprężystości.
Jeżeli oznaczymy przez σ i rzut σ na R i , tzn.
σ i ≡ Ri ⋅σ i
wówczas z równości
σ ⋅ σ ι = σ i ⋅ σ i (i – nie sumować),
I S ⋅ σ = R1 ⋅ σ + K + R m ⋅ σ
otrzymujemy, że
σ = σ1 + σ 2 + K + σ m.
Warunek stanu granicznego (5.30) przyjmuje wówczas postać
σ ⋅ H ⋅σ =
σ 1 ⋅σ 1
χ
2
1
+K+
σ m ⋅σ m
χ m2
≤ 1,
σ i ⋅ σ j = 0, i ≠ j.
(5.34)
Warunek ten opisuje wnętrze elipsoidy sześciowymiarowej w T 2 S .
Jeżeli χ l → ∞ wówczas przestrzeń R l jest przestrzenią stanów
bezpiecznych.
Przyjęcie pewnego stanu naprężenia σ o za stan bezpieczny wymaga
dyskusji jaka została przeprowadzona dla stanów pasywnych w zakresie
odkształceń sprężystych, [14].
Należy podkreślić, że nie zakładaliśmy żadnej zależności między
tensorem sztywności S (podatności C ) i tensorem stanu granicznego H.
Wróćmy do ciał izotropowych – materiału izotropowego. Ponad sto lat
temu pojawiła się praca Hubera pt.: „Właściwa praca odkształcenia jako
miara wytężenia materiału” w mało znanym Czasopiśmie Technicznym,
XXII, we Lwowie w 1904 roku [11]. W pracy tej autor podał warunek
graniczny dla ciał izotropowych w postaci
s ⋅ s ≤ 2 k 2,
91
(5.35)
gdzie „k” jest granicą plastyczności przy czystym ścinaniu. Jest to jeden
z klasycznych warunków, który leży u podstaw matematycznej teorii
plastyczności. Sam autor stał się prekursorem Polskiej Szkoły Mechaniki
ciał odkształcalnych. Niezależnie, warunek w tej postaci podali Mises
w 1913 roku [21] i Hencky w 1924 roku [10].
Rychlewski zajmując się anizotropowym prawem Hooke’a , dotarł do
listu Maxwella [19] pisanym do Thomsona w 1856 roku, w którym
Maxwell sformułował warunek podany później przez Hubera. W liście tym
Maxwell napisał: „I have strong reason for believing that when
α 2 + β 2 + γ 2 − β γ − γ α − α β reaches a certain limit = Rz then element will
begin to give way”.
Warunek s ⋅ s ≤ 2 k 2 znany jest w literaturze jako warunek Hubera –
Mises’a – Hencky’ego. Rychlewski [33] zaproponował aby nazwać go
warunkiem Maxwell’a – Hubera – Mises’a. Warunek ten ma sens
energetyczny. Gęstość energii sprężystej dla ciała izotropowego przyjmuje
postać
1
2
φ (σ ) = σ ⋅ ε (σ ) =
1 2
1
σ +
s ⋅ s,
2K
4G
(5.36)
gdzie K – jest modułem sztywności objętościowej (5.26), natomiast G – jest
modułem ścinania (5.29).
Z wyrażenia na energię (5.36) wynika, że
φ (σ 1 + s ) = φ (σ 1) + φ (s ),
tzn., że całkowita energia jest sumą energii zmiany objętości i energii
dystorsji – tzn. zmiany kształtu. W sformułowaniu Hubera występuje tylko
cześć energii związana ze zmianą postaci φ (s ).
A zatem warunek graniczny
1
φ (s ) ≤ 1 .
h
(5.37)
92
k2
przyjmuje postać warunku Hubera (5.35) dla h =
. Beltrami [3] jako
2G
warunek graniczny przyjął warunek w postaci ograniczenia na wartość całej
energii sprężystej φ (σ ) .
Powstaje jednak pytanie. Jak uogólnić warunek Maxwell’a – Hubera
– Mises’a na ciała anizotropowe? Z anizotropowego prawa Hooke’a (5.1)
1
wynika, że wyrażenie na energię φ = σ ⋅ C ⋅ σ , dla σ = σ 1 + s , przyjmuje
2
postać
2 φ = (σ 1 + s ) ⋅ C ⋅ (σ 1 + s ) = σ 2 1 ⋅ C ⋅ 1 + s ⋅ C ⋅ s + 2 σ 1 ⋅ C ⋅ s
(5.38)
i nie jest sumą energii związanej ze zmianą objętości σ 2 1 ⋅ C ⋅ 1 i energii
związanej ze zmianą kształtu s ⋅ C ⋅ s. Człon 1 ⋅ C ⋅ s powoduje, że
odpowiedź materiału na naprężenia dewiatorowe jest kulista. Burzyński [5]
w 1928 roku proponował obejście tego problemu twierdząc, że nie ma
fizycznych powodów, aby energia nie była sumą φ ( σ 1) i φ (s ) . Warunek
Burzyńskiego jest równoważny założeniu, że
1 ⋅ C ⋅ s = 0.
(5.39)
Ciała o tych własnościach nazywamy objętościowo izotropowymi. Warunek
Burzyńskiego (5.39) nakłada pewne więzy na tensor podatności C. Liczba
niezależnych zmiennych (składowych) tensora C z 21 redukuje się do 16.
Problem energetycznego warunku granicznego został rozwiązany
całościowo w 1984 r. przez Rychlewskiego [33].
STANY ENERGETYCZNIE ORTOGONALNE
Rozpatrujemy przestrzeń tensorów symetrycznych drugiego rzędu
S
T 2 , σ i ε są elementami tej przestrzeni. Zakładamy, że naprężenia
odniesione są do pewnego naprężenia charakterystycznego i są
wielkościami bezwymiarowymi, podobnie jak ε.
Definicja
Dwa stany naprężenia α i β są energetycznie niezależne, jeśli
energia jest addytywną funkcją tych stanów tzn., że
93
φ (α + β ) = φ (α ) + φ (β ).
(5.40)
Ze wzoru na energię (5.3)
2 φ = ( α + β ) ⋅ C⋅ ( α + β ) =α ⋅ C⋅ α + β ⋅ C⋅ β + 2 α ⋅ C⋅ β = φ (α) + φ (β ) + 2 α ⋅ C ⋅ β
wynika, że musi wówczas być spełniony warunek α ⋅ C ⋅ β = 0.
Dla liniowej sprężystości rozdzielność energetyczna oznacza, że naprężenia
α nie pracują na deformacjach C ⋅ β spowodowanych naprężeniami β i na
odwrót.
Definicja
αiβ
nazywamy energetycznie
Dwa stany naprężenia
ortogonalnymi, jeżeli jedno z nich nie pracuje na odkształceniach
spowodowanych przez drugie i na odwrót, co oznacza, że
•
α ⊥ β ≡ α ⋅ C ⋅ β = 0.
(5.41)
•
•
Dwa stany energetycznie ortogonalne będziemy oznaczać przez ⊥ ; α ⊥ β .
Odwzorowanie
(α , β ) →α ⋅ C ⋅ β = β ⋅ C ⋅ α
jest formą biliniową, symetryczną i dodatnio określoną. Może więc być
przyjęte jako definicja iloczynu skalarnego (2.11) zwanego energetycznym
α • β ≡ β •α ≡ α ⋅C⋅ β.
(5.42)
Energia sprężysta dla σ wyraża się wówczas przez energetyczną normę σ ,
tzn., że
1
2
1
2
na sumę prostą
φ (σ ) = σ ⋅ C ⋅ σ = σ • σ .
Każdy rozkład przestrzeni T 2 S
T 2 S = ε1 ⊕ ε1 ⊕ K ⊕ ε κ ,
(5.43)
94
ε α ⊥ε β
•
dla α ≠ β (dowolne dwa elementy z różnych
podprzestrzeni są energetycznie ortogonalne) nazywamy rozkładem
energetycznie ortogonalnym przestrzeni T 2 S dla rozpatrywanego ciała
sprężystego.
Dla dowolnego σ zachodzi równość
taką, że
σ = σ 1 + K + σ κ , σ l ∈ε l , σ α • σ β = 0 dla α ≠ β
i energia sprężysta φ daje się rozłożyć na sumę energii
φ (σ ) = φ (σ 1 ) + φ (σ 2 ) + K + φ (σ κ ).
(5.44)
Takich rozkładów może być wiele.
GŁÓWNY ROZKŁAD ENERGII SPRĘŻYSTEJ
TWIERDZENIE 5.3
Dla dowolnego ciała sprężystego, zadanego tensorem podatności C ,
istnieje dokładnie jedno rozłożenie energetycznie ortogonalne i ortogonalne
przestrzeni T 2 S
T 2 S = P1 ⊕ P2 ⊕ K ⊕ Pρ , ρ ≤ 6
takie, że
•
Pm ⊥ Pn i Pm ⊥ Pn dla m ≠ n
i dokładnie jeden ciąg parami różnych stałych
λ1 ,K, λρ , λm ≠ λn dla m ≠ n
takich, że
C=
1
λ1
P1 +
1
λ2
P2 + K +
1
λρ
Pρ ,
95
gdzie Pk jest ortogonalnym projektorem na Pk , k = 1, 2,K , ρ .
Z rozkładu spektralnego tensora C wynika, że stany własne
odpowiadające różnym wartościom własnym są ortogonalne, tzn. że
w k ⋅ w l = δ kl , k ≠ l
jeżeli
C ⋅ wk =
1
λk
w k (nie sumować).
Jeżeli równość tę pomnożymy stronami przez w l , l ≠ k to otrzymamy, że
wl ⋅ wk = wl ⋅ C ⋅ wk =
1
λk
w k ⋅ w l = 0.
A zatem stany własne C są również stanami energetycznie
ortogonalnymi. Rozkład energii na sumę energii na stanach własnych
tensora C nazywamy głównym rozkładem energetycznie ortogonalnym
[33].
Dowolny stan naprężeń σ można rozłożyć na elementy
podprzestrzeni Pl
σ = σ 1 + K + σ ρ , σ k ⋅ σ l = 0 dla k ≠ l
gdzie σ l = Pl ⋅ σ ∈ P l jest rzutem σ na podprzestrzeń Pl . Stąd wynika, że
1
1
(σ l ⋅ σ l ) 2 = σl = (σ ⋅ Pl ⋅ σ ) 2.
Energia sprężysta dla σ l wyraża się wówczas wzorem
1
2
φ (σ l ) = σ l ⋅ C ⋅ σ l =
σl 2
, l = 1, 2,K, ρ ,
2λl
który otrzymujemy z rozkładu spektralnego tensora C
96
C=
1
λ1
P1 +
1
λ2
P2 + K +
1
λρ
Pρ
w następujący sposób. Mnożąc przez σ l obie strony równości
otrzymujemy, że
σl 2
1
1
σ
⋅
C
⋅
σ
=
, (be sumowania)
C ⋅ σ l = Pl ⋅σ l= σ l i
l
l
λl
λl
λl
1
σl
.
2
2 λl
Główny rozkład energii sprężystej odpowiadający rozkładowi przestrzeni
T 2 S na podprzestrzenie własne Pk dla tensora C przyjmuje postać
φ (σ l ) = σ l ⋅ C ⋅ σ l =
2
σρ 2
σ12 σ22
Φ(σ ) = φ (σ1 + K+ σ ρ ) = φ (σ1 ) + φ (σ 2 ) + K+ φ (σ ρ ) =
+
+ K+
. (5.45)
2 λ1 2 λ2
2 λρ
Wzorem ciał izotropowych można przyjąć, że warunek graniczny (5.34) jest
postaci
σ
1
1
1
σ
σ
φ (σ 1 ) + φ (σ 2 ) + K + φ (σ ρ ) = 12 + 22 + K + ρ2 ≤ 1
h1
h2
hρ
k1
k2
kρ
2
2
2
(5.46)
kα2
gdzie hα =
jest graniczną wartością energii sprężystej dla naprężenia
2 λα
σ α , a mianowicie
1
1 σα
1
2
Φ (σ α ) =
= 2 σα .
hα
hα 2 λα kα
2
(5.47)
Przestrzeń Pα jest przestrzenią stanów bezpiecznych jeśli kα → ∞ .
Warunek graniczny (5.46) wiąże w pewien sposób własności sprężyste ciała
z jego własnościami w stanie granicznym. Tensory S i H są wówczas
współosiowe.
97
INTERPRETACJA ENERGETYCZNA WARUNKU MISES’A
Mises [22] proponując warunek graniczny w postaci
s⋅H ⋅s ≤1
podkreślił, że warunek ten nie ma interpretacji energetycznej. Rychlewski
dowiódł, że dowolna miara kwadratowa naprężenia σ ⋅ Η ⋅ σ ma
jednoznacznie określony sens energetyczny.
TWIERDZENIE 5.4
Dla dowolnego sprężystego ciała zadanego tensorem podatności C
i tensorem stanu granicznego H istnieje dokładnie jedno energetycznie
S
ortogonalne rozłożenie przestrzeni T2 [33]:
•
T2 = H 1 ⊕ H 2 ⊕ K ⊕ H υ , υ ≤ 6, H k ⊥ H l , k ≠ l
S
i dokładnie jeden ciąg parami różnych stałych
h1 , h2 ,K, hυ ; hm ≠ hn , h1 < K < hυ ,
taki, że dla dowolnego stanu naprężenia σ
σ = σ 1 + σ 2 +K+ σ υ , σ l ∈ H l ,
σ ⋅ H ⋅σ =
1
1
1
φ (σ 1 ) + φ (σ 2 ) + K + φ (σ υ ) ,
h1
h2
hυ
(5.48)
gdzie
1
σ ⋅ C ⋅ σ = φ (σ 1 ) + φ (σ 2 ) + K + φ (σ υ ) = φ (σ ).
2
Rozpatruje się zatem dwie formy kwadratowe dodatnio określone :
σ ⋅ C ⋅σ ≥ 0 i σ ⋅ H ⋅σ ≥ 0 .
98
Zakładamy, że operator liniowy L o symetriach wewnętrznych
tensorów C i H działający z T 2 S w T 2 S , elementowi α ∈ T 2 S
przyporządkowuje element α ⇒ L • α.
Z definicji energetycznego iloczynu skalarnego wynika, że :
L • α = L ⋅ (C ⋅ α ) = (L o C ) ⋅ α .
Forma biliniowa α • L • β jest formą symetryczną, ponieważ
α • L • β = α ⋅ (C o L o C ) ⋅ β.
Ma zatem sens zagadnienie
i energetyczne wartości własne
L•χ =
na
energetyczne
(5.49)
stany
1
χ.
2h
własne
(5.50)
Istnieje energetycznie ortogonalny ciąg stanów własnych
χ1 , χ 2 ,K, χ 6
χ k • χ l = δ kl ,
które odpowiadają rzeczywistym wartościom własnym
1 1
1
,
,K,
.
2 h1 2 h2
2 h6
Rozkład spektralny dla L otrzymujemy korzystając z tzw. fundamentalnej
tożsamości (5.6).
Jeżeli tensory ηk stanowią energetycznie ortogonalną bazę w T 2 S tzn.
ηk • ηl = δ kl , to
∧
gdzie α k = α • ηk
α ∈T 2S
1
∨
α1 , α 2 ,K, α 6
αk ∈R .
α = α1 η1 + K + α 6 η6 ,
99
Operator L jest określony na T 2 S jeżeli jest określony na bazie ηk . Wynika
to z faktu, że
L•α = L•(α1 η1 +K+α6 η6 ) =α1 L•η1 +K+α6 L•η6 = (L•η1 ⊗η1 +K+ L•η6 ⊗η6 ) •α.
Otrzymujemy ostatecznie, że
L = L • η1 ⊗ η1 + K + L • η 6 ⊗ η 6 .
(5.51)
Operatorem tożsamościowym jest tensor L = S , ponieważ
S • α = (S o C ) ⋅ α = IS ⋅ α = α.
(5.52)
Dla operatora S fundamentalna tożsamość (5.51) ma postać
S = η1 ⊗ η1 + K + η 6 ⊗ η 6.
(5.53)
Równość ta jest spełniona dla dowolnej bazy η 1 .
Jeżeli jako bazę energetycznie ortonormalną w T 2 S przyjmiemy
energetycznie ortogonalne stany własne η k = χ k otrzymujemy rozkład
spektralny L
L=
1
1
χ1 ⊗ χ1 + K +
χ6 ⊗ χ6 ,
2 h1
2 h6
który jest jednoznaczny dla jednokrotnych wartości
1
.
2 hk
Tensor czwartego rzędu H k
Hk ≡ χ k ⊗ χ k
(nie sumować)
rzutuje energetrycznie element α ∈ T 2 S na podprzestrzeń H k
(5.54)
100
H k • α = (χ k ⊗ χ k ) • α = α k ,
gdzie
α k = (χ k • α )χ k ∈ H k .
Tensor H k nazywamy projektorem energetycznie ortogonalnym.
1
Jeżeli energetyczne wartości własne
nie są jednokrotne, to
2 hk
energetycznie ortogonalne podprzestrzenie własne H k nie są
jednowymiarowe. Rozkład spektralny L (5.54) ma wówczas postać
L=
1
1
1
Η1 +
Η2 + K +
Η κ , κ ≤ 6.
2 h1
2 h2
2 hκ
(5.55)
Warunek Misesa σ ⋅ H ⋅ σ (5.30) można przedstawić w postaci
σ ⋅ H ⋅ σ ≡ σ • (S o H o S ) • σ .
(5.56)
Operator L (5.49) dla warunku Misesa ma zatem postać L = (S o H o S ).
Z rozkładu spektralnego L (5.55) wynika, że
1
1
1
1
σ ⋅H⋅σ =σ •(SoHoS) •σ = σ •H1 •σ +K+ σ •Ηκ •σ = σ •σ1 +K+ σ •σκ =
2h1
2hκ
2h1
2hκ
1
1
1
1
= σ1 •σ1 +K+ σκ •σκ = φ (σ1) +K+ φ (σκ ) ,
2h1
2hκ
h1
hκ
1
gdzie σ = σ 1 + K + σ κ i φ (σ k ) = σ k • σ k (bez sumowania).
2
A zatem dowolny kwadratowy warunek stanu granicznego można
jednoznacznie przedstawić w postaci sumy z pewnymi wagami energii
sprężystych dla energetycznie ortogonalnych części naprężenia.
101
WYZNACZANIE WARTOŚCI WŁASNYCH I ENERGETYCZNIE
ORTOGONALNYCH STANÓW WŁASNYCH
Z równości (5.50)
(S o H o S ) • χ = 1 χ , S o C = I S
2h
wynika, że
SoH⋅χ =
1
χ.
2h
Po nasunięciu z lewej strony tensora C , ( S o C = 1S ) otrzymujemy, że
H⋅χ =
1
C⋅χ
2h
(5.57)
co oznacza, że

1 
 H −
C  ⋅ χ = 0 ⇒ (2 h H − C) ⋅ χ = 0 .
2 h 



1 
1 
C  jest tensorem osobliwym, tzn. det H −
C  = 0 .
Tensor  H −
2
2
h
h




Warunek ten sprowadza się do równania charakterystycznego na h. Po
wyznaczeniu energetycznych wartości własnych hk stany energetycznie
ortogonalne χ k wyznacza się z równania (5.57).
ZALEŻNOŚCI MIĘDZY TENSORAMI C i H
Tensory C i H są tensorami czwartego rzędu o tych samych
symetriach. Z twierdzenia o rozkładzie spektralnym wynika, że można je
przedstawić w postaci (5.18), (5.33)
C=
1
λ1
PI +
1
λ2
PII + K +
1
λρ
Pρ , ρ ≤ 6,
gdzie Pk są projektorami ortogonalnymi na podprzestrzenie własne Pk oraz
102
H=
1
χ
2
1
RI +
1
χ
2
2
R II + K +
1
λm
R m , m ≤ 6,
gdzie R l są projektorami ortogonalnymi na podprzestrzenie własne R l .
Podprzestrzenie Pk i R l na ogół są różne.
Twierdzenie o energetycznej interpretacji formy kwadratowej
σ ⋅ H ⋅ σ nie zakłada żadnej zależności H od C , czyli zależności własności
materiału w stanie granicznym od własności materiału w zakresie
sprężystym.
W ogólnym przypadku rozkład energii na stany energetycznie
ortogonalne różni się od rozkładu na stany własne tensora C . Stany własne
C są ortogonalne i energetycznie ortogonalne. Na ogół nie zachodzi
wynikanie odwrotne.
Lemat
Rozkład na stany energetycznie ortogonalne T 2 S = ε 1 ⊕ ε 2 ⊕ K ⊕ ε m jest
rozkładem ortogonalnym ≡ jeżeli podprzestrzenie te są inwariantne dla
operatora C .
Dwa tensory A i B ∈ T 4 nazywamy zgodnymi jeżeli istnieje w T 4 S
baza w k , w k ⋅ w l = δ kl , złożona ze stanów własnych tensorów A i B ,
taka, że
A = α1 w I ⊗ w I + α 2 w II ⊗ w II + K + α 6 wVI ⊗ wVI ,
B = β1 w I ⊗ w I + β 2 w II ⊗ w II + K + β 6 wVI ⊗ wVI .
Należy zauważyć, że niektóre α k mogą być sobie równe i podobnie β l .
Równości te mogą zachodzić dla różnych stanów własnych. Podprzestrzenie
własne mogą zatem być zupełnie inne.
Jeżeli α k i β l są jednokrotne to podprzestrzenie własne są
jednowymiarowe i takie same. Tensory A i B są wówczas współosiowe.
5.4. Grupy symetrii tensorów czwartego rzędu
103
Będą one również nazywane współosiowymi jeżeli dla wielokrotnych
wartości własnych będą miały te same podprzestrzenie własne.
Tensory A i B są częściowo współosiowe jeżeli podprzestrzenie
własne jednego zawierają się w podprzestrzeniach własnych drugiego.
Jeżeli tensory S i H są współosiowe to rozkład energetycznie
ortogonalny jest ortogonalny.
Z definicji grupy symetrii dla tensora o dowolnej walencji (4.19)
wynika, że dla tensorów czwartego rzędu T grupa symetrii zdefiniowana
jest następująco:
OT = {Q ∈ O; Q ∗ T = T} ,
(5.58)
gdzie Q jest tensorem ortogonalnym drugiego rzędu (4.2) - automorfizmem
trójwymiarowej euklidesowej przestrzeni wektorowej. Generuje on
automorfizmy w przestrzeni czterowymiarowej
Q ∗ T = T ijkl Qei ⊗ Qe j ⊗ Qe k ⊗ Qel .
Tensorami czwartego rzędu są: tensor sztywności S , tensor podatności C
i tensor stanu granicznego H . Można zatem rozpatrywać symetrię tych
tensorów.
Klasyfikacja materiałów liniowo-sprężystych ze względu na symetrię
prowadzi do ośmiu klas symetrii. Podział materiałów liniowo-sprężystych
według symetrii nie ma nic wspólnego z krystalografią [39]. Wynika on
z własności tensorów euklidesowych symetrycznych czwartego rzędu
(z liniowości prawa Hookeà i własności przestrzeni euklidesowej
trójwymiarowej).
Dwiema granicznymi klasami symetrii są:
• pełna anizotropia – brak jakiejkolwiek symetrii - grupa symetrii
OSa = {1,−1},
• izotropia – pełna symetria – grupą symetrii jest całkowita grupa
OSi = O.
104
Pozostałe sześć klas symetrii w kolejności wzrostu symetrii to:
1) symetria monokliniczna - symetria pryzmy o podstawie
nieregularnej,
2) ortotropia - symetria pryzmy o podstawie prostokątnej,
3) symetria trygonalna – symetria pryzmy o podstawie foremnej
trójkątnej,
4) symetria tetragonalna - symetria pryzmy o podstawie kwadratowej,
5) symetria transwersalna – symetria cylindryczna,
6) symetria kubiczna - symetria sześcianu.
Grup symetrii dla poszczególnych klas materiałów poszukujemy
korzystając z rozkładu spektralnego tensora sztywności S (5.17)
S = λI PI + ....λρ Pρ
ρ ≤6
z którego wynika, że jeżeli Q ∈ OS , to
Q ∗ PK = PK .
(5.59)
Oznacza to, że grupą symetrii tensora S jest grupa symetrii zbioru jego
projektorów PK
OS = OPi ∩ OPii ∩ .... ∩ OPρ .
Liczba projektorów PK zależy od liczby różnych modułów Kelvina. Gdy
wszystkie moduły Kelvina są jednokrotnymi pierwiastkami równania
charakterystycznego wówczas przestrzenie własne są jednowymiarowe, zaś
projektory ortogonalne są postaci
PK = ω K ⊗ ω K .
Warunek (5.59) jest w tym przypadku równoważny warunkowi
Q ∗ (ω K ⊗ ω K ) = Q ∗ ω K ⊗ Q ∗ ω K = (Qω K QT ) ⊗ (Qω K QT ) = ω K ⊗ ω K .
Z ostatniej równości wynika, że Qω K QT = ± ω K .
105
Korzystając z podanych warunków symetrii można dla
poszczególnych klas symetrii wyprowadzić postać ortogonalnych
projektorów PK oraz podać dla nich odpowiednią grupę symetrii. Mamy
zatem, że [14]
1) dla symetrii monoklinicznej Oem1 = {1,−1, I e1 } , gdzie e1 jest
wersorem normalnym do płaszczyzny symetrii, I e1 jest tensorem
ortogonalnym
opisującym
lustrzane
odbicie
względem
płaszczyzny o wersorze normalnym e1 ;
2) dla ortotropii OSo = {1,−1, I e1 , I e2 }, gdzie e1 i e 2 są wersorami
normalnymi do płaszczyzn symetrii;
k
2π
3) dla symetrii trygonalnej Oe31t = {1,−1, R e1 3 , I e2 } (k=1, 2), gdzie e1
jest kierunkiem osi symetrii, e 2 normalną do płaszczyzny symetrii
prostopadłej do podstawy pryzmy, Rαe1 ortogonalnym tensorem
opisującym obrót wokół kierunku e1 o kąt α ;
4) dla symetrii tetragonalnej
k
π
Oe41t = {1,−1, I e1 , I e2 , R e12 }(k = 1,2,3) ,
gdzie e1 jest osią symetrii, zaś e1 , e 2 są normalnymi do płaszczyzn
symetrii;
5) dla symetrii transwersalnej Oetr1 = {1,−1, I e1 , I e2 , Rϕe1 }(ϕ ∈ 0,2π ,
gdzie e1 jest osią symetrii, zaś e1 , e 2 są normalnymi do płaszczyzn
symetrii;
k
π
k
π
6) dla symetrii kubicznej O = { 1,−1, I e1 , I e2 , R e1 , R e22 }( k = 1,2,3) ,
c
e1
2
gdzie e1 , e 2 są kierunkami osi symetrii i są normalnymi do
płaszczyzn symetrii.
Ze wzrostem symetrii zmienia się postać pierwszego (5.22) i drugiego
(5.23) indeksu strukturalnego. Pierwszy z nich mówi o wymiarach
podprzestrzeni własnych, drugi zaś o liczbie parametrów opisujących daną
klasę symetrii i ich charakterze.
Materiał o pełnej anizotropii jest opisany przez 21 istotnie różnych
parametrów, które redukują się do dwóch dla izotropii.
Rozdział 6. Funkcje tensorowe
6.1. Funkcje tensorowe argumentu tensorowego
W mechanice ośrodków ciągłych na ogół jedne wielkości fizyczne,
które mają charakter tensorowy, zależą od innych wielkości fizycznych
również o charakterze tensorowym. Zależności te mają charakter funkcji lub
funkcjonałów. I tak na przykład do domknięcia układu równań mechaniki
ośrodków ciągłych należy, dla każdego ośrodka, podać związki wiążące
stan naprężenia z wielkościami charakteryzującymi deformację. Są to tzw.
równania konstytutywne (prawa fizyczne, prawa stanu). Istnieje zatem
konieczność budowania funkcji przyporządkowujących jednym tensorom
drugich.
W rachunku tensorowym można wprowadzać pojęcie funkcji
podobnie jak to się robi w analizie matematycznej.
Jeżeli dany jest zbiór tensorów D ⊂ T p i każdemu tensorowi X ∈ D
przyporządkowujemy jednoznacznie tensor Y ∈ G ⊂ T q , to mówimy, że
na zbiorze D określona jest funkcja tensorowa argumentu tensorowego
f :Tp 
→ T q
Y = f (X).
(6.1)
Ogólnie można rozpatrywać funkcje tensorowe od wielu zmiennych
tensorowych różnego rzędu
Y = f ( X, Z, u, a) .
(6.2)
Gdy wszystkie tensory są skalarami otrzymujemy, jako przypadek
szczególny, zwykłą funkcję rzeczywistą od wielu zmiennych rzeczywistych.
Rozważamy przyporządkowanie
Y = f ( X; H 1 , H 2 ,....H n ) ,
(6.3)
gdzie X - zmienny tensor, H i - tensory parametryczne. W szczególnym
przypadku mamy zależność (6.1)
Y = f (X).
108
Gdy w przestrzeniach T p i T q wybrane są polibazy np. polibazy
proste, wówczas funkcja tensorowa od argumentu tensorowego jest
równoważna układowi 3 q funkcji rzeczywistych od 3 p zmiennych
rzeczywistych:
Y ij ... mn = f ij .... mn ( X kl ... r s ) ,
(6.4)
gdzie
X = X kl ... r s e k ⊗ e l ⊗ .. ⊗ e r ⊗ e s ∈ T p ,
Y = Y ij ...mn e i ⊗ e j ⊗ .. ⊗ e m ⊗ e n ∈ T q .
Forma powyższej zależności zależy od wybranych baz w T p i T q oraz
od postaci funkcji f .
Szczególne przypadki:
a) Funkcja tensorowa argumentu skalarnego
Gdy
Y = f ( x),
x ∈R
np.
Y = f (trX)
(6.5)
mamy do czynienie z funkcją tensorową argumentu skalarnego. Funkcja ta
jest równoważna układowi 3 q funkcji rzeczywistych od jednej zmiennej
rzeczywistej
Y ij ...mn = f ij ....mn ( x) .
(6.6)
Jako argument skalarny można przyjąć czas t, wówczas
Y ij ...mn = f ij ....mn (t ) .
W zagadnieniach termodynamicznych jako zmienna stanu występuje
temperatura.
b) Funkcja skalarna argumentu tensorowego
Jest to funkcja postaci
y = f ( X),
(6.7)
6.2. Grupy symetrii funkcji tensorowych
109
np. y = trX , ( X ∈ T 2 ), y = X ⋅ L ⋅ X ( X ∈ T 2 , L ∈ T 4 ).
Tensor L jest w tej funkcji tensorem parametrycznym.
Funkcja (6.7) jest równoważna jednej funkcji rzeczywistej od 3 p
zmiennych rzeczywistych
y = f ( X kl ... r s ).
(6.8)
c) Funkcje tensorowe dla tensorów drugiego rzędu
W przypadku, gdy zarówno wartość funkcji jak również jej argument
są tensorami drugiego rzędu
Y = f ( X) dla X, Y ∈ T 2 ,
(6.9)
rozpatrujemy funkcje, które w mechanice ośrodków ciągłych występują
najczęściej.
Między przestrzenią tensorów drugiego rzędu T 2 i przestrzenią
macierzy kwadratowych M 2 zachodzi izomorfizm, a zatem zależność
funkcyjna (6.9) między tensorami drugiego rzędu jest równoważna funkcji
macierzowej
j
j
n
(Yi ) = f i ( X m ).
(6.10)
Jest to jednocześnie układ 9 funkcji rzeczywistych od 9 zmiennych
rzeczywistych. Przykładami tego typu funkcji są:
Y = X2 ,
Y =L⋅X,
gdzie L ∈ T 4 i jest tensorem parametrycznym.
Pojęcie grupy symetrii dla tensora zostało wprowadzone już wcześniej
w rozdziale 4 (4.19).
110
A zatem możemy określić grupę symetrii dla tensora X → O X i grupę
symetrii dla tensora Y → OY . Są to tensory ortogonalne spełniające
warunki:
O X = {Q ∈ O; Q ∗ X = X},
(6.11)
OY = {Q ∈ O; Q ∗ Y = Y}.
Definicja
Grupą symetrii funkcji (6.1)
f : T p → Tq
nazywamy zbiór tensorów ortogonalnych O f
O f = {Q ∈ O; Q ∗ f ( X) = f (Q ∗ X)}.
(6.12)
Innymi słowy, do grupy symetrii funkcji f należą takie tensory
ortogonalne, które powodują, że wynik działania funkcji na odwzorowanym
przy ich pomocy argumencie jest taki sam jak wynik odwzorowanej przy
ich pomocy wartości funkcji. Grupy symetrii funkcji nie należy mylić
z grupami symetrii wartości funkcji.
Jeżeli
f : T2 → T2,
wówczas do grupy symetrii funkcji należą tensory ortogonalne spełniające
warunek
O f = {Q ∈ O; Qf ( X)Q T = f (QXQT )}.
Jeżeli O f = O , funkcja f jest funkcją izotropową, jeżeli O f = R
funkcja f jest funkcją hemitropową. W pozostałych przypadkach funkcję
f nazywamy anizotropową.
Funkcjami izotropowymi są np. funkcje
Y = X 2 , Y = trX .
Przykładem funkcji anizotropowej jest prawo Hookeà ε = C ⋅ σ.
111
ZASADY CURIE
Każdą funkcję można interpretować jako prawo, jej argument jest
wówczas przyczyną, zaś jej wartość skutkiem.
Gdy funkcja f jest funkcją izotropową, wówczas jej skutek jest nie
mniej symetryczny niż przyczyna
O X ⊂ OY ⊂ O.
(6.13)
Gdy funkcja f jest funkcją izotropową i wzajemnie jednoznaczną,
wówczas skutek jest tak samo symetryczny jak przyczyna
O X = OY .
W ogólnym przypadku, gdy O f ≠ O , wówczas zachodzi następująca
zależność
OX ∩ O f ⊂ Oy .
(6.14)
Oznacza to, że skutek jest nie mniej symetryczny niż symetria prawa
i przyczyny.
Fakty powyższe znane są w literaturze jako zasady Curie, [34].
Definicja
Funkcję tensorową
Y = f ( X; H 1 , H 2 ,....H n ) , H i ∈ T 2
(6.15)
nazywamy izotropową, gdy tensory H i są postaci H i = hi 1 .
Definicja
Funkcję tensorową
Y = f ( X; H 1 , H 2 ,....H n )
nazywamy izotropową, gdy ma ona tę samą postać we wszystkich układach,
tzn., że
Y • = f ( X • ; H 1 , H 2 ,....H n ) .
Obie definicje są równoważne.
112
6.3. Podstawowe twierdzenia o reprezentacji funkcji
tensorowych izotropowych
TWIERDZENIE 6.1
Funkcja skalarna argumentu tensorowego (6.7) jest izotropowa wtedy
i tylko wtedy, gdy może być przedstawiona w postaci funkcji trzech
niezmienników podstawowych swego argumentu, tzn., że funkcja
izotropowa
y = f ( X) , X ∈ T 2 S
przyjmuje postać
y = f ( I X , II X , III X ),
(6.16)
gdzie I X , II X , III X są niezmiennikami tensora X (3.28). Wynika to
z faktu, że dla funkcji izotropowej postać funkcji we wszystkich układach
jest taka sama.
W ogólnym przypadku można rozpatrywać funkcje skalarne od więcej
niż jednego argumentu tensorowego.
TWIERDZENIE 6.2
Funkcja skalarna od dwóch argumentów tensorowych drugiego rzędu
y = f ( X; Z) , X , Y ∈ T 2 S
(6.17)
jest izotropowa wtedy i tylko wtedy, gdy może być przedstawiona w postaci
y = f ( I X , II X , III X ; I Z , II Z , III Z ; I XZ , II XZ , III XZ , IV XZ ),
(6.18)
gdzie niezmienniki wspólne dla tensorów X i Z są zdefiniowane
następująco:
I XZ = trXZ, II XZ = trX 2 Z , III xz = trXZ 2 , IV XZ = trX 2 Z 2 .
(6.19)
Liczba zmiennych niezależnych w (6.17) redukuje się wówczas do 10
niezmienników podstawowych tensorów X i Z.
6.3. Podstawowe twierdzenia o reprezentacji funkcji tensorowych
113
Powyższe dwa twierdzenia mają ważne znaczenie w mechanice
ośrodków ciągłych. Korzysta się z nich np. przy formułowaniu warunków
granicznych dla ciał izotropowych.
Istotną rolę w mechanice ośrodków ciągłych odgrywają funkcje
tensorowe, których zbiorem argumentów i wartości są tensory symetryczne
drugiego rzędu
s
Y = f ( X) dla X, Y ∈ T2 .
(6.20)
Z definicji potęgi tensora (3.33) wynika, że dowolna potęga tensora
drugiego rzędu jest z nim współosiowa. Tensor X n jest współosiowy
z tensorem X , przy czym w układzie osi głównych tensory te mają postać:
 X I n 00 
 X I 00 




n
n

(X ) =  0 X II 0  - X = 0 X II 0  .


 00 X 
 00 X III n 
III 



Dla tensorów drugiego rzędu zachodzi wzór Cayley-Hamiltona (3.33)
( )
X 3 = I X X 2 + II X X + III X 1 ,
który pozwala wyrazić dowolną potęgę tensora X n przez X 2 , X i 1 ze
współczynnikami zależnymi od niezmienników tensora X − I X , II X , III X .
TWIERDZENIE 6.3
Funkcja tensorowa
S
Y = f ( X) dla X , Y ∈ T 2 .
jest izotropowa wtedy i tylko wtedy, gdy może być przedstawiona
w postaci tensorowego trójmianu kwadratowego
Y = k 0 1 + k1 X + k 2 X 2 ,
(6.21)
114
gdzie współczynniki k 0 , k1 , k 2 są funkcjami trzech podstawowych
niezmienników tensora X − I X , II X , III X lub jego wartości głównych
X I , X II , X III . Twierdzenie to jest konsekwencją twierdzenia CayleyHamiltona w przypadku funkcji izotropowych rozwijalnych w szeregi.
Funkcja (6.21) jest określona jeżeli dana jest postać trzech funkcji
skalarnych k 0 , k1 , k 2 .
Twierdzenie to jest zasadniczym momentem całej teorii funkcji
izotropowych.
Podobnie jak dla funkcji skalarnych argumentu tensorowego tak
również dla funkcji tensorowych drugiego rzędu można rozpatrywać
funkcje od więcej niż jednej zmiennej.
TWIERDZENIE 6.4
Funkcja tensorowa
Y = f ( X, Z) dla X, Y, Z ∈ T2
S
(6.22)
jest izotropowa wtedy i tylko wtedy, gdy może być przedstawiona w postaci
Y = a0 1 + b1 X + b2 Z + c1 X 2 + c 2 (XZ + ZX) + c3 Z 2 + d1 (X 2 Z + ZX2 )
+ d 2 (XZ 2 + Z 2 X) + e1 (X 2 Z 2 + Z 2 X 2 ),
(6.23)
gdzie: a 0 , b1 , b2 , c1 , c 2 , c 3 , d 1 , d 2 , e1 są funkcjami od 10 niezmienników
tensorów X i Z i niezmienników (6.19).
Funkcje tensorowe izotropowe możemy tworzyć korzystając z
najprostszych działań algebry takich jak mnożenie tensorów przez liczbę,
dodawanie, potęgowanie:
Y = kX ,
Y = k 0 1 + k1 X,
Y = k 0 1 + k1 X + k 2 X 2 ,
..................................,
Y = k 0 1 + k1 X + .......k n X n .
6.3. Podstawowe twierdzenia o reprezentacji funkcji tensorowych
115
Dochodzimy w ten sposób do idei szeregu potęgowego
∞
Y = ko 1 + ∑ ki Xi .
(6.24)
i =1
Uwaga: Szeregi mają sens tylko wówczas, gdy każdy z 9 szeregów dla
składowych jest zbieżny.
W ten sposób mamy możliwość uogólnienia rozwijalnych w szeregi
funkcji elementarnych jednej zmiennej na tensory. Na przykład, dla funkcji
wykładniczej
∞
xi
y = f ( x) = e x = 1 + ∑ ,
i =1 i!
możemy napisać, że
∞
Xi
Y = f ( X) = e X = 1 + ∑ .
(6.25)
i =1 i!
Symbol f będzie dalej oznaczał wyjściową funkcję np.
sin(..), (..) , ln(..).
TWIERDZENIE 6.5
Osie główne tensora Y będącego funkcją izotropową tensora X
pokrywają się z osiami głównymi tensora X , przy czym jeżeli
Y = f (X) dla X, Y ∈ T2 ,
to wartości główne tych tensorów związane są związkami
YI = f ( X I ), YII = f ( X II ), YIII = f ( X III ).
jak
Uwaga:
a) Twierdzenie jest słuszne oczywiście tylko wówczas , gdy osie
główne istnieją,
b) Nie należy sądzić, że w układzie osi nie głównych mają miejsce
np. związki:
Y12 = f ( X 12 ), Y12 = e12 i inne tego typu.
Gdy szereg tensorowy jest uogólnieniem funkcji elementarnej takiej
e (..) , ln(..), sin(..) to współczynniki w szeregu k i są liczbami.
116
Dla tensorów możemy wprowadzić szeregi ogólniejsze w postaci
∞
Y = k 0 ( X I , X II , X III )1 + ∑ k i ( X I , X II , X III ) X i ,
(6.26)
i =1
które odpowiadają funkcjom izotropowym postaci:
Y = f ( X, X I , X II , X III ) .
6.4. Wzór Sylwestra-Lagrangeà
Dane są trzy dowolne funkcje:
φ ( X I , X II , X III ),
ψ ( X I , X II , X III ), χ ( X I , X II , X III ).
Funkcja
f (t) = f (t; XI , XII , XIII ) =
(t − XII )(t − XIII )
(t − XIII )(t − XI )
(t − XI )(t − XII )
φ+
ψ+
χ
(XI − XII )(XI − XIII ) (XII − XIII )(XII − XI ) (XIII − XI )(XIII − XII )
ma następującą własność
f ( X I ; X I , X II , X III ) = φ ( X I , X II , X III ) ,
f ( X II ; X I , X II , X III ) = ψ ( X I , X II , X III ),
f ( X III ; X I , X II , X III ) = χ ( X I , X II , X III ).
(6.27)
Stąd wynika, że funkcja tensorowa izotropowa
Y = f (X) =
(X − X II 1)(X − X III 1)
(X − X III 1)(X − X I 1)
(X − X I 1)(X − X II 1)
φ+
ψ+
χ
( X I − X II )(X I − X III ) ( X II − X III )(X II − X I )
( X III − X I )(X III − X II )
mająca w osiach głównych postać:
(6.28)
YI = φ ( X I , X II , X III ),
YII = ψ ( X I , X II , X III ) ,
YIII = χ ( X I , X II , X III )
117
(6.29)
przeprowadza wartości główne tensora X w wartości główne tensora Y
według z góry zadanego prawa dla każdej wartości YI , Y II , YIII (6.27).
Wniosek ten ma zasadnicze znaczenie dla eksperymentatora. Istotnie,
wystarczy stwierdzić, że tensory X i Y są związane zależnością izotropową
i że związki YI , YII , YIII z X I , X II , X III mają wykrytą w doświadczeniu
postać, aby wykorzystując podany wzór wypisać związek tensorowy słuszny
w dowolnym układzie.
Podany wzór (6.28) nosi nazwę wzoru Sylwestra-Lagrangeà.
Wzór Sylwestra-Lagrangeà można wykorzystać do wykrycia
zależności współczynników k 0 , k1 , k 2 od niezmienników tensora X we
wzorze (6.21)
Y = k 0 1 + k1 X + k 2 X 2
jeżeli zadany jest kształt funkcji Y = f (X) .
Bezpośrednie rozwinięcie funkcji w szereg (o ile jest rozwijalna)
i wykorzystanie wzoru Cayley-Hamiltona prowadzi do skomplikowanych
rachunków. Wykorzystując natomiast wzór Sylwestra-Lagrangeà, po
uporządkowaniu wyrazów przy odpowiednich potęgach tensora
otrzymujemy, że
k0 =
XII XIII f (XI )
XIII XI f (XII )
XI XII f (XIII )
,
+
+
(XI − XII )(XI − XIII ) (XII − XIII )(XII − XI ) (XIII − XI )(XIII − XII )
−k1 =
(XII + XIII) f (XI )
(XIII + XI ) f (XII )
(XI + XII ) f (XIII)
+
+
, (6.30)
(XI − XII )(XI − XIII) (XII − XIII)(XII − XI ) (XIII − XI )(XIII − XII )
118
k2 =
f (X I )
f ( X II )
f ( X III )
+
+
.
( X I − X II )(X I − X III ) ( X II − X III )(X II − X I ) ( X III − X I )(X III − X II )
Z faktu, że między niezmiennikami i wartościami głównymi tensora
X zachodzą zależności
I X = X I + X II + X III ,
II X = −( X I X II + X II X III + X III X I ) ,
III X = X I X II X III
(6.31)
wynika, że współczynniki k o , k1 , k 2 można również wyrazić przez
niezmienniki.
Postępowanie powyższe ma znaczenie dla praktyki przy wykrywaniu
postaci związków konstytutywnych.
EFEKTY POYNTINGA I KELVINA
W mechanice ośrodków ciągłych bardzo istotną rolę odgrywa
tensorowy trójmian kwadratowy (6.21)
Y = k 0 1 + k1 X + k 2 X 2
(6.32)
s
dla tensorów drugiego rzędu symetrycznych, tzn. gdy X, Y ∈ T2 .
Równanie tensorowe (6.32) jest wówczas równoważne układowi
sześciu równań skalarnych na składowe
Y i j = k 0 δ ι j + k1 X i j + k 2 X i m X m j
w przypadku, gdy
Y = Y i jei ⊗ e j ,
X = X m ne m ⊗ en .
Każdy z tensorów X, Y można rozłożyć na część kulistą i część
dewiatorową
I
I
X = X 1 + D X , Y = Y 1 + DY
(6.33)
3
3
i zastąpić wyjściowy związek tensorowy przez dwa równania:
119
•
zależność skalarną między śladami tensorów X i Y
trY = 3k 0 + k1trX + k 2 trX 2
(6.34)
2
I Y = 3k 0 + k1 I X + k 2 (2 II X + I X )
•
oraz zależność tensorową między ich dewiatorami
2 2 2
D Y = (k1 + 2k 2 )D X + k 2 {( D X ) 2 − ( I X + II X )1} .
(6.35)
9
3
Teorie, w których k 2 ≠ 0 są nazywane teoriami tensorowonieliniowymi. Uwzględniają one tzw. efekty drugiego rzędu.
W całym szeregu teorii należy postawić w (6.32) warunek
Y = 0 dla X = 0 , tzn., że f (0) = 0
z którego wynika, że zachodzi równość
k 0 (0,0,0) = 0 .
Nawet w tym przypadku, gdy tensor X jest dewiatorem ( trX = 0 )
tensor Y może mieć część kulistą ( trY ≠ 0 ). Ze związku między częściami
kulistymi tych tensorów (6.34) wynika, że
I Y = 2k 2 II X .
(6.36)
Taką sytuację nazywamy efektem Poyntinga.
Gdy k 2 = 0 tensorowy trójmian kwadratowy (6.32) przyjmuje postać
Y = k 0 1 + k1 X
(6.37)
i jest związkiem tensorowo liniowym. Ze względu na zależność
współczynników k 0 , k1 od niezmienników tensora X jest on jednak w
dalszym ciągu związkiem nieliniowym od składowych tensora X. Taki
związek nazywamy quasiliniowym.
W tym przypadku między częściami kulistymi i dewiatorami tensorów
X, Y zachodzą zależności (6.34), (6.35)
I Y = 3k 0 + k1 I X ,
(6.38)
D Y = k1 D X .
(6.39)
120
TWIERDZENIE 6.6
Warunkiem koniecznym i dostatecznym na to, aby zależność między
tensorami była quasiliniowa jest podobieństwo ich dewiatorów (6.39).
Twierdzenie to ma ważne znaczenie dla zastosowań. W badaniach
eksperymentalnych wystarczy sprawdzić, że zachodzi związek
( µ - parametr Lode`go)
(6.40)
aby pokazać, że związek fizyczny jest quasiliniowy.
Parametr Lode`go dla tensora Y jest zdefiniowany następująco
µY = µX ,
( DY II − DY I ) + ( DY II − DY III )
Y − YIII
= 2 II
− 1.
Y
Y
D I − D III
YI − YIII
Analogicznie parametr Lode`go definiuje się dla tensora X.
Można pokazać, że jeżeli parametry Lode`go dla dwóch tensorów są
sobie równe (6.40), wówczas spełnione są równości
DY I
D Y II
D Y III
=
=
= k1
D X I D X II D X III
tzn., że zachodzi podobieństwo dewiatorów i związek fizyczny jest
quasiliniowy.
Jeżeli w związku quasiliniowym (6.37) (k 2 = 0) współczynnik
k 0 = k 0 ( I X , II X , III X ) zależy od niezmienników tensora X , wówczas może
zajść sytuacja, że dla I X = 0 mamy z (6.38)
µY =
I Y = 3k 0 (0, II X , III X ) ≠ 0.
(6.41)
Sytuację taką nazywamy efektem Kelvina.
TWIERDZENIE 6.7
Związek tensorowy Y = f (X) jest liniowy i jednorodny ze względu
na składowe tensora X wtedy i tylko wtedy, gdy w (6.34) i (6.35)
k 0 = cI X , c = const , k1 = const , k 2 = 0.
Związek o tej postaci zapisuje się zwykle w składowych jako
Yij = λtrXδ ij + 2 µX ij ,
λ , µ = const.
(6.42)
121
6.5. Funkcje tensorowe potencjalne
Jest to najprostsza możliwa zależność izotropowa między dwoma
tensorami.
Przykład:
Jeżeli przyjmiemy, że
Yij = σ ij , X ij = ε ij
to otrzymujemy prawo Hookeà (5.1) liniowej sprężystości dla ciał
izotropowych.
Nasze rozważania dotyczyły funkcji tensorowej jednego argumentu
tensorowego. W zastosowaniach musimy uzależnić niekiedy tensor Y od
kilku tensorów X i , np. tensor naprężenia zależy od tensora deformacji,
tensora prędkości deformacji oraz innych tensorów nie mających charakteru
mechanicznego.
Jest zatem sens rozpatrywać funkcje tensorowe postaci
Y = F ( X 1 , X 2 ,...., X k ; H 1 , H 2 ,..., H m ),
gdzie H i tensory parametryczne.
Można pokazać, że jeżeli wszystkie tensory są symetryczne, to niezależnych
tensorów może być tylko 6, a niezależnych dewiatorów tylko 5.
6.5. Funkcje tensorowe potencjalne
Funkcję izotropową
Y = f (X)
nazywamy potencjalną, jeżeli istnieje funkcja
niezmienników tensora X - I X , II X , III X taka, że
Yij =
∂W
∂X ij
.
skalarna
W
od
(6.43)
Funkcję skalarną W = W ( I X , II X , III X ) nazywamy potencjałem.
Wykonując różniczkowanie potencjału po składowych tensora X
otrzymujemy następujące wyrażenie
122
Yij =
∂W
∂W ∂I X
∂W ∂II X
∂W ∂III X
=
+
+
.
∂X ij ∂I X ∂X ij ∂II X ∂X ij ∂III X ∂X ij
Po wykorzystaniu wzorów na pochodne niezmienników tensora X po
jego składowych
∂I X
∂II X
= δ ij ,
= X ij − I X δ ij ,
∂X ij
∂X ij
∂III X
= X im X mj − I X X ij − II X δ ij (6.44)
∂X ij
funkcję potencjalną (6.43) sprowadza się do tensorowego trójmianu
kwadratowego
Y=(
∂W
∂W
∂W
∂W
∂W
∂W
− IX
− II X
)1+ (
− IX
)X+
X 2 . (6.45)
∂III X
∂I X
∂II X
∂III X
∂II X
∂III X
W tym tensorowym trójmianie kwadratowym współczynniki k 0 , k1 , k 2
zależą tylko od jednej funkcji skalarnej W . Jest to zatem przypadek
szczególny ogólnej postaci tensorowego trójmianu kwadratowego (6.32).
Gdy potencjał nie zależy od trzeciego niezmiennika, to powyższy
związek tensorowy jest związkiem quasiliniowym. Taka sytuacja ma
miejsce, gdy rozpatrujemy stowarzyszone prawo płynięcia dla warunku
plastyczności Hubera-Misesa.
Rozdział 7. Pola tensorowe
7.1. Pola skalarne, wektorowe i tensorowe
Przestrzeń euklidesowa punktowa jest jednym z podstawowych
modeli matematycznych przestrzeni fizycznej – formy bytu materii. Model
ten jest fundamentem fizyki klasycznej. Podstawowym narzędziem
mechaniki ośrodków ciągłych są pola tensorowe na podobszarach
przestrzeni euklidesowej. Pojęcie przestrzeni euklidesowej wektorowej ∋ n
było już wprowadzone wcześniej (patrz Rozdział 2. Struktury algebraiczne).
Jest to przestrzeń liniowa nad ciałem liczb rzeczywistych, której elementami
są wektory z dodatkową operacją iloczynu skalarnego. Wprowadziliśmy
również przestrzeń euklidesową punktową ε n , jako zbiór związany z ∋ n
przez zadane odwzorowanie
ε n × ε n →∋ n ;
( A, B ) ∈ ε n × ε n ⇒ AB ∈∋ n .
Odwzorowanie to spełnia następujące aksjomaty:
∧
AB= −BA
A, B∈εn
∧
A, B, C∈εn
AB= AB+ BC
∧ ∧
∨
O∈εn X ∈εn x∈εn
OX = x,
gdzie x − promień wektor punktu X względem wybranego punktu O .
Obierając w ε n punkt O można zdefiniować jedno-jednoznaczne
przyporządkowanie pomiędzy punktami z ε n a wektorami ze
stowarzyszonej przestrzeni ∋ n
o
o
ϕ
ϕ :ε n
−1
∋n ,
→
: ∋ n → εn ,
o
o
ϕ ( X ) = OX = x
ϕ
−1
(x ) = O + x = X .
(7.1)
124
Punkt O nazywamy początkiem w
εn
przy odwzorowaniu 0 ϕ . Wektor
ϕ ( X ) = OX = x nazywamy promień wektorem (promieniem wodzącym)
o
punktu X przy odwzorowaniu 0 ϕ .
Przestrzeń ε n nie jest przestrzenią liniową. Można jednak przenieść
do niej struktury przestrzeni wektorowej jako odpowiednie operacje na
promieniach wodzących.. Struktura ta zależy wyboru punktu O. Ostatni
symbol dodawania w (7.1) nie jest dodawaniem w zwykłym sensie.
Sumowanie to oznacza, że punkt O jest początkiem wektora x , zaś jego
końcem jest punkt X.
Reperem w przestrzeni punktowej ε n stowarzyszonej z ∋ n nazywamy
każdą parę (O, e i ) , gdzie O ∈ ε n , e i ∈∋ n . Punkt O jest punktem zaczepienia
repera, zaś wektory e i są bazą w ∋ n .
Baza e i jest ortonormalna, gdy e i ⋅ e j = δ ij . Wektory bazy są
wzajemnie ortogonalne.
W mechanice ośrodków ciągłych przyjmuje się, że przestrzeń fizyczna
jest modelowana trójwymiarową punktową przestrzenią euklidesową ε 3 z
reperem (O, e i ) (i =1,2,3).
Przestrzeń euklidesową punktową
ε3
definiuje się czasem jako zbiór
R = R × R × R , gdzie R jest ciałem liczb rzeczywistych.
Wybierając w ∋3 bazę ortonormalną i k ( i k ⋅ i l = δ kl ) otrzymujemy
wzajemnie jednoznaczne odwzorowanie
3
ik
ik
ψ : ∋3 → R 3
ψ (x ) = (x ⋅ i1 , x ⋅ i 2 , x ⋅ i 3 ).
Odwzorowanie
Φ =i ψ o o ϕ :
k
ε
3 →
R3
(7.2)
(7.3)
jest izomorfizmem ε 3 w R 3 zależnym od repera (O , ik ) względem struktur
przeniesionych z ∋3 .
Należy starannie odróżniać przestrzeń punktową od przestrzeni wektorowej
i obie od przestrzeni liczbowej.
7.2. Układy współrzędnych kartezjańskich w ε 3
125
Definicja
Polem tensorowym na podzbiorze D ⊂ ε 3 nazywamy odwzorowanie
f : D → Tq ,
(7.4)
X ∈ D ⇒ f (X ) ∈Tq .
Odwzorowanie to przyporządkowuje w sposób jednoznaczny punktom X
należącym do obszaru D tensory rzędu q.
Polem tensorowym nazywamy zatem funkcję tensorową określoną na
podzbiorze przestrzeni euklidesowej punktowe ε 3 .
W szczególności mamy :
f ( X ) = ϕ ( X ) ∈R
pole skalarne ,
f ( X ) = v ∈ ∋3
pole wektorowe,
f (X ) = T ∈T2
pole tensorowe o walencji 2.
Przykładem pola tensorowego o walencji 1- pola wektorowego na ε 3 jest
pole promienia wodzącego z O. Jest to odwzorowanie ε 3 → ∋3 .
Jedno-jednoznaczna zależność między punktami z ε 3 a wektorami z ∋3
(7.1) ustalona poprzez przyjęcie początku w ε 3 pozwala każdemu polu
tensorowemu na przestrzeni punktowej przyporządkować funkcję tensorową
argumentu wektorowego
f o o ϕ −1 :
∋3 → T q .
W zastosowaniach mechaniki ośrodków ciągłych pewne informacje
dotyczące wielkości tensorowych uzyskujemy w postaci liczbowej. A zatem
na pewnym etapie naszych rozważań jesteśmy zmuszeni do pewnej
arytmetyzacji teorii. W przestrzeniach tensorowych T q uzyskiwaliśmy taką
arytmetyzację wprowadzając bazy. W odpowiednich polibazach tensory
punktowe były reprezentowane układem 3 q liczb.
Arytmetyzację opisu podzbiorów w ε 3 i pól tensorowych na ε 3
uzyskujemy wprowadzając w ε 3 układy współrzędnych.
126
W przestrzeni euklidesowej punktowej ε 3 można zawsze wprowadzić
absolutny układ prostokątnych współrzędnych kartezjańskich. Przestrzeń
fizyczna modelowana przestrzenią euklidesową punktową jest ponadto
przestrzenią jednorodną i izotropową. Jednorodność przestrzeni jest
równoważna założeniu, że prawa fizyczne nie zależą od położenia
obserwatora lub ściślej od miejsca wystąpienia zjawiska. Natomiast
izotropowość oznacza, że wszystkie kierunki w przestrzeni są równoważne.
Z tych dwóch własności wynika równoważność wszystkich przestrzennych
układów współrzędnych użytych do opisu badanego zjawiska. A zatem
wybór układu współrzędnych jest dowolny.
Definicja
Układem odniesienia w
ε3
nazywamy każdą uporządkowaną
→
czwórkę punktów {O; P1 , P2 , P3 } taką, że wektory OPi
są liniowo
niezależne. Punkt O jest początkiem układu odniesienia {O; P1 , P2 , P3 } .
Układ odniesienia nazywamy ortogonalnym, gdy
→
→
OPi ⋅ OPj = 0
dla i ≠ j ,
i ortonormalnym (lub kartezjańskim), gdy
→
→
OPi ⋅ OPj = δ ij .
Pojęcie układu odniesienia jest ściśle związane z pojęciem repera w
ε3 .
Reperem w ε 3 nazywaliśmy parę {O; e i } złożoną z punktu O - punktu
zaczepienia repera i bazy (tzn. liniowo niezależnej trójki uporządkowanych
wektorów e i ∈ ∋3 ).
→
→
Jeżeli przyjmiemy, że e i = OP i to reper {O; OPi } nazywamy reperem
układu odniesienia {O; P1 , P2 , P3 } .
→
Biorąc układ odniesienia {O; P1 , P2 , P3 } i jego reper {O; e i } ( e i = OP i )
możemy dowolny punkt X ∈ ε 3 przedstawić w postaci
X = O + x = xiei .
127
Zdefiniowane w ten sposób liczby x i nazywamy współrzędnymi punktu X
w układzie odniesienia {O; P1 , P2 , P3 } . Gdy e i ⋅e j = δ ij to współrzędne x i
nazywamy kartezjańskimi.
W dalszych rozważaniach bazę ortonormalną będziemy oznaczać przez i k ,
zaś współrzędne kartezjańskie przez z k . Sam układ współrzędnych
kartezjańskich oznaczać będziemy przez {z k } z reperem kartezjańskim
{O; i k } Rys. 2.
Obserwator w konfiguracji kartezjańskiej {z k } przestrzeń punktową
ε3
traktuje jak przestrzeń liczbową R × R × R = R 3 (układ trzech liczb),
a przestrzeń tensorów o walencji q jak przestrzeń 3 q układów liczb.
Posługując się układem kartezjańskim będziemy wszystkie indeksy pisać na
jednym, dolnym poziomie. W dalszym ciągu obowiązuje konwencja
sumacyjna Einsteina.
Jeżeli ustalony jest układ współrzędnych {z k } poprzez zadanie repera
{O; i k } , wówczas punktowi P ∈ ε 3 przyporządkowana jest trójka liczb z k ,
→
które są składowymi promień wektora p = OP w bazie i k
p = zk i k ,
gdzie z k = p ⋅ i k .
Rys. 2. Zmiana układu współrzędnych kartezjańskich.
128
Z jednorodności i izotropowości przestrzeni
ε 3 wynika, że można również
wprowadzić inny układ kartezjański {z ∗ m } z reperem {O ∗ ; i ∗ m }.
Punktowi P ∈ ε 3 odpowiadają wówczas dwa różne promień wektory:
→
→
p = OP i p ∗ = O ∗ P . Zwykle przyjmuje się, że O = O ∗ (pomija się
translację) i wówczas
p = p∗ = zk i k = z ∗mi∗m .
(7.5)
W ten sposób jednemu punktowi P ∈ ε 3 zostały przyporządkowane dwie
trójki liczb.
Z geometrii analitycznej wiadomo, że dwie bazy ortonormalne są
związane ze sobą następującą zależnością
i ∗ m = α mk i k ,
(7.6)
gdzie macierz transformacji jest macierzą kosinusów kierunkowych,
a mianowicie
α mk = i ∗ m ⋅ i k = cos(i ∗ m , i k ) .
(7.7)
Równość i ∗ m = α mk i k można odwrócić i rozłożyć bazę
Mamy wówczas zależność
i k = β km i ∗ m .
Z warunku
i k = β kmα ml i l = δ kl i l
wynika, że macierz α ml posiada następujące własności:
β kmα ml = δ kl ,
α mk = β km .
i k w bazie i ∗ m .
(7.8)
Macierz odwrotna jest równa macierzy transponowanej. Macierz o
tych własnościach nazywana jest macierzą ortogonalną. Ostatecznie
otrzymujemy, że
i k = α mk i *m = cos(i *m , i k ) i *m .
(7.9)
129
Nie wszystkie z dziewięciu składowych macierzy α mk są niezależne. Można
pokazać, że tylko 3 są dowolne (porównaj kąty Eulera w mechanice ciała
stałego).
Znając rozkład jednej bazy w drugiej można wyprowadzić wzór na
transformację składowych wektora p przy zmianie układu współrzędnych
(7.5). Spełnione są następujące zależności:
z ∗ m = α mk z k ,
(7.10)
∗
z k = α mk z m .
W przestrzeni tensorów drugiego rzędu, dla baz ortonormalnych,
polibazami będą diady:
i k ⊗ il , i∗m ⊗ i∗n .
Składowymi tensora T ∈ T2 w układzie kartezjańskim {z k } będzie macierz
Tkl taka, że jeżeli
T = Tkl i k ⊗ i l ,
to
Tkl = i k ⋅ T ⋅ i l .
Macierz składowych tensora T przy zmianie układu współrzędnych (7.6)
transformuje się w następujący sposób:
T ∗ mn = α mk α nl Tkl .
(7.11)
Tensor T w nowej polibazie ma wówczas postać
T = T ∗ mn i ∗ m ⊗ i ∗ n .
(7.12)
∗
Macierze Tkl i T mn nazywamy składowymi tensora T odpowiednio
w układzie kartezjańskim {z k } i {z ∗ m } .
Otrzymane wzory transformacyjne są wynikiem przyjętych definicji
tensorów i mogą być również traktowane jako definicje tych obiektów
geometrycznych. Jest to tzw. definicja transformacyjna zgodnie z którą np.
tensorem drugiego rzędu nazywamy taki obiekt geometryczny, który w
dowolnym układzie współrzędnych kartezjańskich {z k } zadany jest
macierzą liczb Tkl , które przy zmianie układu współrzędnych (7.10)
transformują się zgodnie ze wzorem (7.11).
Definicja transformacyjna pozwala, przy znajomości składowych tensora w
130
jednym układzie współrzędnych kartezjańskich, wyznaczyć składowe tego
tensora w dowolnym innym układzie kartezjańskim, o ile znany jest sposób
przejścia od jednego układu do drugiego [9].
7.3. Współrzędne krzywoliniowe
W konkretnych zagadnieniach mechaniki ośrodków ciągłych
wygodniej jest czasami posługiwać się nie układem współrzędnych
kartezjańskich, ale układem współrzędnych np. walcowym lub sferycznym.
Współrzędne ogólniejsze niż kartezjańskie będziemy nazywali
współrzędnymi krzywoliniowymi.
Rachunek tensorowy, w swym tradycyjnym ujęciu, zwykle
rozpoczyna się od układu współrzędnych, co stwarza problem z pokazaniem
niezależności tensorów od układu uważaną za istotę rachunku tensorowego.
W ujęciu prezentowanym w tym wykładzie pojęcia tensorów, funkcji
tensorowych itd. było wprowadzone bez jakichkolwiek układów
współrzędnych. Tylko w ten sposób idea niezależności od układu była we
właściwy sposób wykazana.
Wprowadzając układy współrzędnych chcemy nawiązać do podejścia
klasycznego oraz umożliwić arytmetyzację teorii, o ile jest to konieczne.
Definicja
Każdy homomorfizm x obszaru D przestrzeni euklidesowej
punktowej ε 3 na obszar G ⊂ R 3
x:D →G
nazywamy układem współrzędnych w D , a trójkę liczb
P∈D
(7.13)
{x1 ( P), x 2 ( P), x 3 ( P)} = x k ( P) ,
nazywamy współrzędnymi (krzywoliniowymi) punktu P w układzie {x k } .
Jedną klasę układów współrzędnych stanowią wcześniej wprowadzone
układy kartezjańskie.
W układzie kartezjańskim {z m } dowolnemu punktowi P ∈ D
przyporządkowana jest trójka liczb {z1 , z 2 , z 3 }. Są to składowe wektora
(7.5)
→
p = OP = z k i k .
Na punktach P ∈ D można zadać trzy dowolne funkcje
131
x k = x k ( P) = x k ( z1 , z 2 , z 3 ).
(7.14)
Jeżeli jakobian przekształcenia jest różny od zera, tzn. jeżeli
∂x k
J = det(
) ≠ 0,
(7.15)
∂z m
to punktowi P ∈ D można przyporządkować jednoznacznie trzy inne liczby
{x 1 , x 2 , x 3 } i zależność x k od z m można odwrócić. Otrzymujemy
wówczas, że
z m = z m ( x 1 , x 2 , x 3 ).
(7.16)
W ten sposób w przestrzeni punktowej ε 3 został wprowadzony układ
współrzędnych krzywoliniowych {x k } Rys. 3.
Rys. 3. Układ współrzędnych krzywoliniowych.
Geometrycznym odpowiednikiem układu współrzędnych {x k } w D
jest następujący zbiór linii i powierzchni:
x k linią nazywamy obraz w D zbioru
{( x 1 , x 2 , x 3 ); x i = const , i ≠ k } ⊂ D ,
x p , x q powierzchnią nazywamy obraz w D zbioru
{( x 1 , x 2 , x 3 ); x i = const , i ≠ p, i ≠ q} ⊂ D .
Jest oczywistym, że linia x k jest częścią wspólną dwóch powierzchni.
132
Zdefiniowany w ten sposób zbiór linii i powierzchni nazywamy siecią
geometryczną układu {x k } . Linie x k nazywamy osiami układu
krzywoliniowego, Rys.3.
LOKALNA BAZA I KOBAZA . MACIERZ METRYCZNA
Z wzajemnie jednoznacznej zależności między składowymi x k i z m
→
(7.16) wynika, że promień wektor p = OP (7.5) można przedstawić w
postaci
p = z m i m = z m ( x k )i m .
(7.17)
xk
układu
współrzędnych
Równanie
wektorowe
linii
k
krzywoliniowych ma zatem postać p = p( x ) dla wybranego k i przy
ustalonych pozostałych dwóch współrzędnych, np. dla k=1 równanie
p = p( x 1 ) jest równaniem parametrycznym krzywej x 1 .
Z geometrii różniczkowej wynika, że wektory styczne do linii układu
otrzymuje się w wyniku różniczkowania równania wektorowego (7.17) linii
po parametrze zmiennym wzdłuż tej linii. Mamy zatem, że
∂p ∂z
(7.18)
g k ≡ k = mk i m .
∂x
∂x
Wersory i m są stałe dla układu.
Trójkę wektorów g k (7.18) zależną od punktu P ∈ D nazywamy bazą
lokalną układu. Wektory te są funkcją punktu i zmieniają się przy przejściu
od punktu do punktu. W ten sposób układ współrzędnych krzywoliniowych
{x k } określony został przez reper lokalny {P; g k ( P)} .
Definicję wektorów bazy lokalnej g k można traktować jako ich rozkład w
bazie układu kartezjańskiego i m . Wykorzystując równość
∂z m ∂z m ∂x k
= δ mn
=
∂z n ∂x k ∂z n
otrzymujemy z (7.18) rozkład bazy układu kartezjańskiego w bazie lokalne
∂x k
im =
gk .
(7.19)
∂z m
Wektory bazy lokalnej g k (7.18) układu krzywoliniowego nie są na
ogół wersorami ani też wektorami wzajemnie ortogonalnymi. Można je
133
lokalnie unormować, wprowadzając w ten sposób bazę fizyczną g ( k ) . Jest to
lokalna baza jednostkowa g ( k ) = 1. Otrzymujemy ją
wektorów bazy g k przez jego długość
g
g (k ) = k , (nie sumować po k).
gk
dzieląc każdy z
(7.20)
Długości hk = g k wektorów bazy lokalnej g k nazywamy parametrami
Lamego siatki krzywoliniowej .
Macierzą metryczną układu krzywoliniowego {x k } nazywamy
macierz utworzoną z iloczynów skalarnych wektorów bazy lokalnej (7.18)
g kl ≡ g k ⋅ g l .
(7.21)
Jest to macierz symetryczna, ponieważ iloczyn skalarny jest przemienny. Na
diagonalnej tej macierzy znajdują się kwadraty parametrów Lamego. Jeżeli
baza lokalna jest bazą ortogonalną, wówczas macierz metryczna jest
macierzą diagonalną. Jeżeli baza jest bazą ortonormalną, wówczas macierz
metryczna jest macierzą jednostkową.
Wektory bazy lokalnej g k nie są na ogół wzajemnie ortogonalne. Można
zatem wprowadzić lokalnie inną trójkę wektorów g l zwanych bazą dualną
lub kobazą takich, że spełniona jest równość
gl ⋅gk = δ l k .
(7.22)
Z równości tej wynika, że dla każdych dwóch wektorów bazy istnieje
wektor z kobazy ortogonalny do nich. Wprowadzając za Siedovem [38]
oznaczenie
[g k , g l ] ≡ g k × g l (iloczyn wektorowy)
można wektory kobazy przedstawić w postaci
g1 =
[g 2 , g 3 ] 2 [g 3 , g1 ] 3 [g1 , g 2 ]
,g =
,g =
,
g
g
g
(7.23)
gdzie g = det( g kl ).
Rozkładając wektory bazy w kobazie otrzymujemy interpretację
macierzy metrycznej. Równość g k = g kl g l oznacza, że służy ona do
obniżania indeksów i jest macierzą współczynników rozkładu wektorów
bazy w kobazie.
134
Macierzą odwrotna do macierzy g kl będzie macierz g mn = g m ⋅ g n , która
jest macierzą współczynników rozkładu wektorów lokalnej kobazy w bazie
g m = g mn g n i służy do podnoszenia indeksów.
WSPÓŁRZĘDNE KONTRA I KOWARIANTNE
Wektory bazy i kobazy stanowią dwie trójki wektorów liniowo
niezależnych. Każda z nich generuje przestrzeń wektorową ∋3 . Dowolny
wektor z tej przestrzeni można zatem jednoznacznie rozłożyć w tych bazach
v = v k g k = vl g l .
(7.24)
Liczby v k nazywamy składowymi kontrawariantnymi wektora v , zaś
liczby v l składowymi kowariantnymi tego wektora. Między tymi
składowymi zachodzą następujące zależności:
v k = g kl v l , v l = g lk v k ,
które wynikają ze wzorów na rozkład jednej bazy w drugiej.
Dla tensora drugiego rzędu T ∈ T 2 , w zależności od lokalnego
stowarzyszenia bazowego, otrzymujemy cztery różne macierze reprezentacji
tensora
l
T = T kl g k ⊗ g l = Tkl g k ⊗ g l = T k l g k ⊗ g l = Tk g k ⊗ g l .
(7.25)
Macierz T kl nazywamy macierzą składowych kontrawariantnych tensora
T ∈ T 2 , macierz Tkl macierzą składowych kowariantnych, dwie pozostałe
macierze są nazywane składowymi mieszanymi tensora. Między tymi
składowymi zachodzą następujące związki
n
Tkl = T mn g mk g nl = T m l g mk = Tk g nl .
(7.26)
Z zależności (7.26) wynika istotna rola macierzy metrycznej przy przejściu
od jednej reprezentacji tensora do drugiej.
Jeżeli układ {x k } jest układem współrzędnych kartezjańskich, to jego
lokalna baza staje się bazą całego układu, jest ortonormalna i baza pokrywa
się z kobazą. Nie ma wówczas różnicy między składowymi kontra
i kowariantnymi. Macierz metryczna jest wówczas macierzą jednostkową
g kl = δ kl .
Rozdział 8. Różniczkowanie i całkowanie pól
tensorowych
Polem tensorowym o walencji q (rzędu q) na podzbiorze D ⊂
nazywamy odwzorowanie
ε3
f : D → Tq,
P ∈ D ⇒ f ( P) ∈ T q .
Odwzorowanie to przyporządkowuje w sposób jednoznaczny punktom
obszaru D tensory rzędu q.
Do opisu podzbiorów w przestrzeni euklidesowej punktowej służą nam
układy współrzędnych. W przestrzeni euklidesowej można zawsze
wprowadzić absolutny układ prostokątnych współrzędnych kartezjańskich
{z k } .Wybór układu współrzędnych jest dowolny Rozdział 7.
Układem współrzędnych {z k } w D nazywamy każdy homomorfizm
obszaru D na obszar G ⊂ R 3 , a trójkę liczb
{z1 ( P ), z 2 ( P ), z3 ( P )} = z k ( P ) ∈ R 3
nazywamy współrzędnymi kartezjańskimi punktu P w tym układzie.
Poza układami kartezjańskimi można wprowadzić inne układy
współrzędnych tzw. krzywoliniowe.
W przypadku układów kartezjańskich reperem w przestrzeni punktowej ε 3
będzie para {O; i k } , gdzie O jest początkiem układu współrzędnych {z k } ,
zaś wektory i k stanowią bazę ortonormalną w ∋ 3 ( i k ⋅ i l = δ kl ) .
Współrzędnymi punktu P będą trójki liczb
→
z k = OP⋅ i k = p ⋅ i k .
(8.1)
Dowolny tensor T ∈ T q w bazie i k można przedstawić w postaci
T = Tijkl ...mn i i ⊗ i j ⊗ i k ⊗ i l ⊗ ... ⊗ i m ⊗ i n .
(8.2)
136
Rozdział 8. Różniczkowanie i całkowanie pól tensorowych
Pole tensorowe T o walencji q, po wyborze układu współrzędnych,
jest równoważne układowi 3 q funkcji rzeczywistych od trzech zmiennych
rzeczywistych, a mianowicie
T = T( P),
Tijkl ...mn = Tijkl ...mn ( z p ),
gdzie T ∈ Tq , i, j , k , l ,..., m, n, p = 1,2,3.
Pola tensorowe tak interpretowane można różniczkować i całkować
o ile są spełnione założenia dotyczące różniczkowania i całkowania funkcji
rzeczywistych od wielu zmiennych rzeczywistych.
8.1. Operacje różniczkowe na polach tensorowych
Klasyczne określenie pochodnej funkcji rzeczywistej jednej zmiennej
rzeczywistej jako granicy stosunku przyrostu wartości funkcji do przyrostu
argumentu nie może być adoptowane do funkcji tensorowych, ponieważ nie
jest zdefiniowane dzielenie tensorów przez tensory.
Powszechnie przyjęte są dwa sposoby uogólnienia definicji pochodnej na
funkcje tensorowe:
a) uogólnienie pochodnej wykorzystujące pojęcie styczności i przybliżenia
liniowego - co prowadzi do tzw. różniczki Frechetà,
b) uogólnienie pochodnej wykorzystujące pojęcie pochodnej kierunkowej,
co prowadzi do tzw. różniczki Gateaux.
GRADIENT POLA TENSOROWEGO
Dane jest pole tensorowe T( P) rzędu q określone na podobszarze
D⊂
ε3
T = T( P),
P ∈ D,
T ∈Tq.
Rozpatrywane pole jest na ogół polem niejednorodnym, tzn. zmienia swoją
wartość przy przejściu od punktu do punktu.
Lokalną zmienność tego pola można określić definiując pochodną
kierunkową pola w kierunku wersora µ
T( P + αµ ) − T( P )
137
d
T( P + αµ ) α =0 .
dα
α
α →0
Jeżeli istnieje granica tego wyrażenia dla każdego µ , to
d
∂ µ T( P ) =
TP (αµ) α =0 = [ DTP (0)]µ ,
dα
gdzie TP jest już funkcją tensorową argumentu wektorowego promień
wektorów względem punktu P.
∂ µ T( P ) = lim
≡
Pochodna kierunkowa pola tensorowego rzędu q jest również tensorem
rzędu q. Ostatni wzór można również zapisać
∂T
≡ gradT ⋅ µ.
(8.3)
∂µ
Definicja
Gradientem pola tensorowego T( P ) ∈ T q nazywamy pole tensorowe
∇T( P ) ≡ gradT( P ) = DTP (0) ∈ T q+1 .
Ze wzoru na pochodną kierunkową (8.3) wynika, że zarówno lewa jak
i prawa strona równości jest tensorem q- tego rzędu. Równość ta jest
prawdziwa dla dowolnego kierunku µ . Z twierdzenia o dzieleniu tensorów
(Dodatek) wynika wówczas, że gradT jest tensorem o walencji q+1.
N- tym gradientem pola tensorowego T( P) nazywamy pole
∇ n T ≡ ∇(∇ n −1T) ∈ Tq + n .
Operacja gradientu podnosi rząd tensora o 1. Gradient pola tensorowego jest
miarą niejednorodności pola.
Przykłady:
POLE SKALARNE ϕ ( P)
Jedną z geometrycznych charakterystyk pola skalarnego jest istnienie
powierzchni ekwipotencjalnych, tzn. powierzchni stałości pola
ϕ ( P) = const.
Gradient pola skalarnego (8.3) jest polem wektorowym, gradφ ∈ T 1 = ∋ 3 .
138
Można pokazać, że:
a) prędkość zmiany pola skalarnego jest największa w kierunku
określonym wektorem gradϕ ,
b) wektor gradϕ jest prostopadły do powierzchni ekwipotencjalnej,
c) prędkość zmiany pola skalarnego w dowolnym kierunku µ jest
określona przez gradϕ ⋅ µ.
Powyższe fakty wynikają z własności iloczynu skalarnego. Gradient pola
skalarnego jest wektorem. Pochodna kierunkowa (8.3) pola skalarnego jest
równa rzutowi wektora gradϕ na kierunek µ. Mamy zatem, że
gradϕ ⋅ µ = gradϕ cos( gradϕ , µ ) .
Lewa strona tej równości jest największa, gdy
cos( gradϕ , µ) = 1.
Taka równość jest spełniona dla wektorów równoległych , tzn. , że wówczas
gradφ µ . Tym samym własność a) pola skalarnego została udowodniona.
Jeżeli kierunek µ jest wersorem stycznym do powierzchni
ekwipotencjalnej, wówczas pole skalarne w tym kierunku nie ulega zmianie.
Ze wzoru na pochodną kierunkową tego pola otrzymujemy, że
gradϕ ⋅ µ = 0.
Iloczyn skalarny dwóch wektorów zeruje się dla wektorów prostopadłych.
Skoro wektor µ był styczny do powierzchni ekwipotencjalnej to wektor
gradϕ jest do niej prostopadły. W ten sposób została udowodniona
własność b). Własność c) wynika z samej definicji pochodnej kierunkowej.
POLE WEKTOROWE v ( P)
Gradient pola wektorowego jest polem tensorowym o walencji 2,
gradv = P ∈ T 2 .
(8.4)
139
Tensor P posiada wszystkie własności tensora drugiego rzędu. Jest on na
ogół tensorem niesymetrycznym. Można dokonać jego symetryzacji,
zwężenia itd.
Definicja
Dywergencją pola wektorowego v nazywamy pole skalarne
otrzymane z pola tensorowego P (8.4) przez dokonanie na nim operacji
zwężenia
~
divv ≡ P = trP = tr ( gradv).
(8.5)
Jeżeli ponadto pole wektorowe v jest gradientem pola skalarnego
v = gradϕ , to skalar
divv = divgradϕ = ∆ϕ
(8.6)
nazywamy laplasjanem pola skalarnego ϕ .
Operacja dywergencji obniża rząd pola tensorowego o 1.
Definicja
Na polu wektorowym v można określić inną operację, zwaną rotacją
tego pola. Rotacja pola wektorowego jest wektorem
rotv = u .
(8.7)
Jest to pole wektorowe u , które jest wektorem dwoistym do pola P T
(Dodatek).
( u) i = ε ikl vl , k .
(8.8)
Operacja rotacji nie zmienia rzędu pola.
Operacje dywergencji i rotacji można zdefiniować dla dowolnego pola
tensorowego, przy czym nie są one wówczas określone jednoznacznie.
Jeżeli T( P) jest polem tensorowym rzędu q, to i-tą dywergencją tego
pola nazywamy pole tensorowe rzędu q-1 postaci
( i , q +1)
~
div T = grad T ,
(i )
1 ≤ i ≤ q.
(8.9)
140
Takich dywergencji może być q. Można się umówić, że pierwszą
dywergencję (i=1) nazywamy dywergencją pola.
Jeżeli T( P) jest polem tensorowym rzędu q, to i-tą rotacją tego pola
nazywamy pole tensorowe rzędu q, które jest dwoiste do tensora gradT
względem i-tej składowej tensora T.
Z pojęciem gradientu, dywergencji i rotacji pól tensorowych związane
są następujące definicje:
a) Pole wektorowe v ( P) nazywamy potencjalnym w obszarze
D ⊂ ε 3 , jeżeli na D określone jest pole skalarne ϕ ( P) takie, że
w każdym punkcie P ∈ D spełniona jest równość
v = gradϕ .
b) Pole wektorowe v ( P) nazywamy solenoidalnym w obszarze
D ⊂ ε 3 , jeżeli na D określone jest pole wektorowe u( P) takie,
że w każdym punkcie P ∈ D spełniona jest równość
v = rotu .
c) Pole wektorowe v ( P) nazywamy bezwirowym w obszarze
D ⊂ ε 3 , jeżeli w każdym punkcie P ∈ D
rotv = 0.
d) Pole wektorowe v ( P) nazywamy nierozbieżnym (bezźródłowym)
w obszarze D ⊂ ε 3 , jeżeli w każdym punkcie P ∈ D
divv = 0.
Z powyższych definicji wynikają następujące wnioski:
• każde pole potencjalne jest polem bezwirowym rotv = ro tg radϕ = 0,
• każde pole solenoidalne jest polem bezźródłowym divv = divrotu = 0 .
Można udowodnić, że są prawdziwe następujące równości:
div(ϕv ) = ϕdivv + vgradϕ ,
div(u × v ) = vrotu − urotv,
rot (u × v ) = ( v ⋅ grad )u − (u ⋅ grad ) v + udivv − vdivu,
divgradϕ = ∆ϕ ,
rotrotv = graddivv − ∆v.
8.2. Różniczkowanie pól tensorowych w układach kartezjańskich
141
8.2. Różniczkowanie pól tensorowych w układach
kartezjańskich
Do opisu podobszarów D w przestrzeni euklidesowej punktowej ε 3
wprowadzamy układy współrzędnych. W przestrzeni euklidesowej ε 3
można zawsze wprowadzić absolutny układ współrzędnych kartezjańskich.
Można
również
wprowadzić
współrzędne
ogólniejsze
zwane
współrzędnymi krzywoliniowymi.
Pole tensorowe, po wyborze układu współrzędnych, reprezentowane
jest układem funkcji rzeczywistych od trzech zmiennych rzeczywistych.
Pola tensorowe tak rozumiane możemy różniczkować o ile są spełnione
założenia dotyczące różniczkowania funkcji rzeczywistych.
Sposób różniczkowania pól tensorowych, jako układu funkcji
rzeczywistych od trzech zmiennych rzeczywistych, zależy w sposób istotny
od wyboru układu współrzędnych. Różniczkowanie tych pól jest najprostsze
w układach kartezjańskich ze względu na istnienie absolutnej bazy.
W układzie współrzędnych kartezjańskich {z k } o reperze (O ; i k )
punktowi P ∈ D przyporządkowane są trójki liczb z k nazywane
współrzędnymi kartezjańskimi punktu P w tym układzie.
→
Jeżeli wektor p = OP jest promień wektorem punku P względem punktu
O to współrzędnymi kartezjańskimi punktu P są liczby
z k = p ⋅ i k , i k ⋅ i l = δ kl .
Pole tensorowe rzędu q T( P) w bazie ortonormalnej i k jest
reprezentowane układem 3 q funkcji rzeczywistych od trzech funkcji
rzeczywistych Tmn...kl = Tmn..kl ( z p ).
Pola tensorowe w ten sposób rozumiane można różniczkować względem
zmiennych przestrzennych z k .
Definiujemy operator różniczkowy nabla, który w układzie
współrzędnych kartezjańskich ma postać
∇≡
∂
⊗ im.
∂z m
(8.10)
142
Stąd wynika, że
gradT = ∇T =
∂T
⊗ im .
∂z m
(8.11)
Jeżeli
T = Tkl ...rs i k ⊗ i l ⊗ ... ⊗ i r ⊗ i s ,
wówczas
∇T = Tkl ...rs , m i k ⊗ i l ⊗ ... ⊗ i r ⊗ i s ⊗ i m ,
(8.12)
gdzie przez przecinek oznaczono różniczkowanie po zmiennych
przestrzennych. W układach kartezjańskich baza jest stała i wychodzi poza
znak różniczkowania.
Dla pola T( P) można wyznaczać dalsze gradienty tego pola. Każdy
następny podnosi rząd tensora o 1. Tensorem rzędu q+2 będzie tensor
∇(∇T) = Tkl ...rs , m n i k ⊗ i l ⊗ ... ⊗ i r ⊗ i s ⊗ i m ⊗ i n .
Laplasjanem tego pola nazywamy tensor o walencji q postaci
∆T = ∇2T =Tkl...rs,mm ik ⊗il ⊗...⊗ir ⊗is = (Tkl...rs,11+Tkl...rs,22+Tkl...rs,33 )ik ⊗il ⊗...⊗ir ⊗is .
Dla pola skalarnego ϕ ( P) = ϕ ( z m ) otrzymujemy z (8.10), że
∂ϕ
∇ϕ =
i m = ϕ , m i m = ϕ ,1 i 1 + ϕ , 2 i 2 + ϕ , 3 i 3 ,
∂z m
∆ϕ = ϕ ,11 +ϕ , 22 +ϕ , 33 .
(8.13)
(8.14)
Dla pola wektorowego v ( P) = v( z k ) = vl ( z k )i l gradient pola jest
tensorem
∂v
∇v =
⊗ i m = v, m ⊗i m = vl , m i l ⊗ i m
(8.15)
∂z m
i macierz pochodnych cząstkowych vl , m jest macierzą reprezentacji tensora
drugiego rzędu w bazie i k .
Stosując operację zwężenia gradientu pola wektorowego – pola
tensorowego drugiego rzędu ∇v , otrzymujemy skalar zwany dywergencją
8.3. Różniczkowanie pół tensorowych w układach krzywoliniowych
143
pola wektorowego v
divv = ∇~
v = v m , m = v1 ,1 + v 2 , 2 + v3 , 3 .
(8.16)
Dla pola tensorowego T( P) o walencji q można wyznaczyć q różnych
dywergencji, i-tą dywegencją pola T( P) nazywamy tensor rzędu q-1
postaci
( i , q +1)
~
∇T = Tkl ...i ...us ,i i k ⊗ i l ⊗ ... ⊗ i u ⊗ i s .
Rotacją pola wektorowego v nazywamy wektor u dwoisty do
gradientu pola
u = rotv = ∇ × v = ε mkl vl , k i m .
(8.17)
Wektor ten ma składowe
rotv = (v3 , 2 −v 2 , 3 )i 1 + (v1 , 3 −v3 ,1 )i 2 + (v 2 ,1 −v1 , 2 )i 3 ,
(8.18)
które się zerują jeżeli gradient pola wektorowego jest tensorem
symetrycznym.
Dla pola tensorowego T( P) o walencji q można wyznaczyć q różnych
rotacji, i-tą rotacją pola T( P) nazywamy tensor rzędu q postaci
i
rotT = ε jmi Tkl ...i...us , m i k ⊗ i l ⊗ ... ⊗ i u ⊗ i s ⊗ i j .
8.3. Różniczkowanie pól tensorowych w układach
krzywoliniowych
W przestrzeni fizycznej, która jest modelowana przestrzenią
euklidesową punktową można zawsze wprowadzić układ kartezjański. W
konkretnych zagadnieniach mechaniki wygodniej jest czasami posługiwać
się ogólniejszymi układami zwanymi krzywoliniowymi (punkt 7.3).
Układem współrzędnych w obszarze D ⊂ ∋ 3 nazywamy każdy
homomorfizm {x m } obszaru D na obszar G ⊂ R 3 , a trójki liczb
{x1 ( P), x 2 ( P), x 3 ( P)} = x k ( P) ,
P∈D
144
nazywamy współrzędnymi (krzywoliniowymi) punktu P w tym układzie.
Jedną klasę układów stanowiły układy kartezjańskie w których każdemu
punktowi P przyporządkowano trójki liczb z m ( P). Na punktach P można
zadać trzy dowolne funkcje
x k = x k ( P) = x k ( z1 , z 2 , z 3 ) = x k ( z m ).
(8.19)
Jeżeli jakobian przekształcenia J
∂x k
J ≡ det(
)≠0
∂z m
to zależność (8.19) jest odwracalna i punktowi P ∈ D można
przyporządkować trzy inne trójki liczb x k ( P) i w ten sposób został
wprowadzony układ współrzędnych krzywoliniowych.
Z geometrii różniczkowej wynika, że jeżeli równanie wektorowe linii
układu ma postać
r
p = OP = z m i m = z m ( x k )i m ,
to wektory styczne w punkcie P do krzywych układu współrzędnych dane
są wzorami
∂p ∂z
g k = k = mk i m .
(8.20)
∂x
∂x
Trójkę wektorów g k określonych w punkcie P nazywamy bazą lokalną
układu.
Układ krzywoliniowy określony jest przez reper naturalny układu
{P; g k ( P)} , który jest reperem lokalnym.
Wektory g k stanowią bazę w ∋ 3 . Każdą z baz g k i i m można rozłożyć
w drugiej. Definicję wektorów g k można traktować jak ich rozkład w bazie
i m . Odwracając zależność (8.20) otrzymujemy , że
im =
∂x k
gk .
∂z m
(8.21)
145
Bazą dualną lub kobazą do bazy g k nazywamy bazę , którą spełnia równość
gl ⋅ gk = δ l k .
Pole tensorowe T( P) , po zadaniu układu krzywoliniowego, można
różniczkować po zmiennych przestrzennych x k . W tym celu korzystamy z
operatora nabla, który w tym przypadku ma postać
∇≡
∂
⊗ gk .
k
∂x
(8.22)
Stąd wynika, że
∇ϕ = gradϕ =
∂ϕ k
g = ϕ,k g k ,
k
∂x
∇v = gradv =
∂v
⊗ g k = v, k ⊗g k ,
∂x k
∇T = gradT =
∂T
⊗ g k = T, k ⊗g k .
k
∂x
(8.23)
Aby wyrazić operację gradientu przez składowe pól tensorowych w
układach krzywoliniowych należy wyznaczyć pochodne
v ( x m ), k =
∂v
,
∂x k
T( x m ), k =
∂T
.
∂x k
W tym miejscu pojawia się istotna różnica między różniczkowaniem
pól tensorowych w układach kartezjańskich i w układach krzywoliniowych.
Różniczkując pole tensorowe w układach kartezjańskich
różniczkujemy jedynie reprezentację tego pola w bazie absolutnej i k , która
jest stała. Różniczkując pole tensorowe w układach krzywoliniowych
musimy pamiętać, że baza g k i kobaza g l są bazami lokalnymi i zmieniają
się przy przejściu od punktu do punktu. Należy zatem zróżniczkować
również wektory bazy i kobazy, tzn. wyznaczyć pochodne
146
∂g m
∂g n
i
.
∂x k
∂x k
(8.24)
Z definicji wektorów bazy lokalnej (8.20) wynika, że
∂g m
∂g
∂ 2p
∂ 2p
=
=
= mk .
k
m
k
k
m
∂x
∂x ∂x
∂x ∂x
∂x
(8.25)
Taka równość drugich pochodnych jest cechą przestrzeni riemanowskich.
Można zatem napisać, że rozkład pochodnej bazy w bazie będzie miał
postać
∂g m
= Γ l mk g l .
(8.26)
∂x k
Wielkości trój-indeksowe Γ l mk są symetryczne po parze indeksów m, k
(8.25). Są one nazywane symbolami Christoffela II rodzaju. Symbolami
Christoffela I rodzaju nazywamy wielkości
l
Γn ,mk = g nl Γmk
.
Symbole Christoffela wyznaczamy z (8.20) i (8.21)
∂g m
∂ 2 zn
∂ 2 z n ∂x l
∂ ∂z n
=
=
=
(
i
)
i
gl .
n
n
∂x k ∂x k ∂x m
∂x k ∂x m
∂x k ∂x m ∂z n
Z porównania (8.26) i (8.27) otrzymujemy, że
∂ 2 z n ∂x l
l
Γ km ≡
.
∂x k ∂x m ∂z n
Pochodną wektorów kobazy wyznaczamy korzystając z definicji
gm ⋅ gn = δ m .
Różniczkując obie strony tej równości otrzymujemy zależność
n
∂g m n
∂g n
g
+
g
=0
m
∂x k
∂x k
(8.27)
(8.28)
147
z której wynika, że
∂g
∂g n
g m k = − m g n = −Γ l mk g l ⋅ g n = −Γ l mk δ ln = −Γ n mk .
∂x k
∂x
Mnożąc obie strony tej równości przez g k otrzymujemy, że
∂g n
n
= −Γmk
gk .
k
∂x
Ostatecznie wzór na pochodną wektorów kobazy przyjmuje postać
∂g n
= −Γmn k g k .
m
∂x
gk ⋅ gm
(8.29)
Symbole Christoffela nie transformują się jak obiekt o walencji 3. Można je
jednak wyrazić przez pochodne macierzy metrycznej
g mn = g m ⋅ g n .
(8.30)
Jeżeli wprowadzimy oznaczenia
∂g
∂g
g mn , k ≡ mn
, g m , k ≡ mk ,
k
∂x
∂x
to różniczkując macierz metryczną (8.30) otrzymujemy
g mn , k = g m , k ⋅g n + g m ⋅ g n , k .
Ponieważ g m , k = g k , m , to zachodzi równość
g mn , k + g km , n − g nk , m = 2g m ⋅ g n , k = 2g m Γnkl g l .
Stąd wynika, że
Γnkl =
1
( g mn , k + g km , n − g nk , m ) g lm .
2
POJĘCIE POCHODNEJ KOWARIANTNEJ
W definicji gradientu pola tensorowego (8.23) występują pochodne
tego pola względem zmiennych przestrzennych. Dla pola wektorowego
v( P)
∇v = v, k ⊗g k .
(8.31)
Znając pochodne po zmiennych przestrzennych wektorów bazy (8.26)
i kobazy (8.29) możemy wyznaczyć ich gradienty. Mamy mianowicie, że
148
l
∇g m = g m , k ⊗g k = Γmk
gl ⊗ gk ,
(8.32)
∇g = g , k ⊗g = −Γ g ⊗ g .
n
n
k
n
kl
l
k
W celu wyrażenia gradientu pola wektorowego (8.31) przez jego
składowe w układzie krzywoliniowym przedstawiamy go w bazie
v = v mg m .
Po zróżniczkowaniu tego wyrażenia otrzymujemy
∂v l
∂v m
∂v ∂v m
m l
m ∂g m
l
g
g
g
(
+ v m Γmk
)g l .
v
+
v
Γ
=
+
=
=
m
mk l
m
∂x k
∂x k
∂x k
∂x k ∂x k
(8.33)
Wyrażenie występujące w nawiasie nazywamy pochodną kowariantną
wektora v od jego składowych kontrawariantnych. Wprowadzamy
następujące oznaczenie
∂v l
l
).
v l ;k ≡ ( k + v m Γmk
∂x
Wzór na gradient pola wektorowego (8.31) przyjmuje teraz postać
∇v = v l ; k g l ⊗ g k .
(8.34)
Ze wzoru tego wynika, że macierz pochodnych kowariantnych v l ;k
jest reprezentacją tensora drugiego rzędu. Macierz samych pochodnych
cząstkowych taką reprezentacją nie jest.
Gdy układ współrzędnych krzywoliniowych staje się układem
kartezjańskim, wówczas symbole Christoffela (8.28) zerują się i pochodna
kowariantna jest równa pochodnej cząstkowej.
Dla pola skalarnego pochodna kowariantna jest równa pochodnej
cząstkowej
ϕ;k = ϕ ,k .
149
8.4. Operacje całkowe na polach tensorowych
Ze wzoru na gradient pola wektorowego (8.34) wynika, że
k
divv = ∇~
v = v l ;k g l ⋅ g k = v l ;k δ l = v k ;k .
(8.35)
rotv = v m ; k g × g .
k
m
Znając pochodne wektorów bazy i kobazy po zmiennych
przestrzennych układu krzywoliniowego możemy wyznaczać gradienty
dowolnych pól tensorowych i wyrażać je przez składowe tych pól w tych
układach. Jeżeli np.
T = T m ng m ⊗ g n
to z (8.23) wynika, że
∇T = T, k ⊗g k = (T m n g m ⊗ g n ), k ⊗g k ≡ T m n ; k g m ⊗ g n ⊗ g k ,
gdzie
(T mngm ⊗gn ),k = T mn ,k gm ⊗gn +T mngm ,k ⊗gn +T mngm ⊗gn ,k =
l
= T mn ,k gm ⊗gn +T mnΓmk
gl ⊗gn −T mngm ⊗Γksn gs = (T mn ,k +T i nΓikm −T m j Γknj )gm ⊗gn =
T mn ;k gm ⊗gn .
Przez ; (średnik) oznaczono pochodną kowariantną.
Korzystając z przedstawionego algorytmu można wyrażać gradienty
dowolnych pól tensorowych przez ich składowe w układzie
krzywoliniowym.
Dla pól tensorowych można rozpatrywać całki krzywoliniowe,
powierzchniowe i objętościowe, które sprowadzają się odpowiednio do
całek riemanowskich pojedynczych, podwójnych i potrójnych, gdyż znane
z analizy matematycznej twierdzenia całkowe mają również zastosowanie
w przypadku pól tensorowych.
150
I. CAŁKI KRZYWOLINIOWE
W przestrzeni fizycznej ε 3 dany jest
regularna) opisany równaniem parametrycznym
z k = z k (α ) , dla α 1 ≤ α ≤ α 2 .
łuk
L -(krzywa
(8.36)
Funkcja wektorowa p(α ) = z k (α )i k jednej zmiennej rzeczywistej jest
odcinkami ciągła i różniczkowalna.
Elementem zorientowanym łuku L nazywamy wektor elementarny
dp(α ) = dz k (α )i k skierowany stycznie do łuku w kierunku zgodnym z jego
parametryzacją. Jego długość nazywamy elementarną długością łuku dl .
Z równania parametrycznego łuku (8.36) wynika, że
dz
dz k = k dα ,
(8.37)
dα
dz k
gdzie wielkości
są składowymi wektora stycznego do łuku L .
dα
Elementarną długość łuku dl wyznaczamy ze wzoru
1
1
dz dz 1
dl = [dp(α ) ⋅ dp(α )] 2 = (dz k dz k ) 2 = ( k k ) 2 dα .
(8.38)
dα dα
Stąd wynika, że całkowita długość łuku L jest równa całce
L = ∫ dl =
L
Ia.
α2
∫
α
1
dz k dz k
dα .
dα dα
CAŁKA KRZYWOLINIOWA PIERWSZEGO RODZAJU
- CAŁKA KRZYWOLINIOWA PO ŁUKU NIEZORIENTOWANYM
Całką krzywoliniową z pola tensorowego T( P ) ∈ T q
po łuku
niezorientowanym L nazywamy całkę krzywoliniową z tego pola po
elementarnej długości łuku (8.38)
∫ Tdl .
L
151
Całka ta, po wyborze układu współrzędnych, jest równoważna układowi 3 q
całek riemanowskich pojedynczych postaci
α2
1
dz r dz r
∫L Tijkl...mn ( z p )dl = α∫ Tijkl ...mn ( z p (α ))( dα dα ) 2 dα .
1
(8.39)
W wyniku całkowania nie zmienia się rząd tensora. Mamy tyle całek jaki
jest wymiar przestrzeni tensorów o walencji q, tzn. 3 q .
Ib. CAŁKA KRZYWOLINIOWA DRUGIEGO RODZAJU
- CAŁKA KRZYWOLINIOWA PO ŁUKU ZORIENTOWANYM
T( P ) ∈ T q
Całą krzywoliniową z pola tensorowego
po łuku
zorientowanym (8.37) L nazywamy całkę postaci
∫ T ⊗ dp .
L
Całka ta jest
pojedynczych
3 q +1
całek
riemanowskich
( z p )dz r = ∫ Tijkl ...mn ( z p (α ))
dz r
dα .
dα
(8.40)
równoważna
układowi
α2
∫T
ijkl .. mn
α1
L
W wyniku całkowania otrzymujemy tensor o walencji q+1.
W szczególności można rozpatrywać całki krzywoliniowe postaci
(ν , q +1)
~
∫ T ⊗ dp ,
gdzie
1 ≤ ν ≤ q.
L
Takich całek w zależności od indeksu ν może być q. Dokonujemy
zwężenia tensora T z wektorem dp . Takich zwężeń może być tyle jaka jest
walencja tensora T .
Każda z tych całek jest równoważna układowi 3 q −1 całek riemanowskich
pojedynczych
152
∫T
α2
ijkl ... r ... mn
L
( z p )dz r = ∫ Tijkl ...r ...mn ( z p (α ))
α1
dz r
dα .
dα
Przykład:
Całkę krzywoliniową po krzywej zamkniętej z pola wektorowego
v (p) postaci
α2
∫ v(p) ⋅ dp = ∫ vk ( z m )dz k = ∫ vk ( z m (α ))
L
α1
L
dz k
dα
dα
(8.41)
nazywamy cyrkulacją pola wektorowego po tej krzywej.
II. CAŁKI POWIERZCHNIOWE
Płat powierzchniowy S w przestrzeni fizycznej ε 3 opisuje funkcja
wektorowa od dwóch zmiennych. Równanie parametryczne płata S ma
postać
p = p(α , β ) = z k (α , β )i k ,
(α1 ≤ α ≤ α 2 ,
β 1 ≤ β ≤ β 2 ) (8.42)
gdzie linie α , β
tworzą układ krzywoliniowy współrzędnych
powierzchniowych.
Wektory elementarne skierowane stycznie do linii α i linii β
w kierunku zgodnym z ich parametryzacją oznaczamy przez dp (1) i dp ( 2) .
Ich składowe w układzie kartezjańskim są związane z parametryzacją
zależnościami
dz k
(1)
=
∂z k
dα ,
∂α
dz k
( 2)
=
∂z k
dβ .
∂β
(8.43)
Jeżeli przez dS oznaczymy pole powierzchni elementarnego płata, to
elementem zorientowanym tego płata nazywamy wektor dS o składowych
dS k = nk dS , gdzie wektor n jest wersorem prostopadłym do elementarnego
płata dS .
Korzystając z własności iloczynu wektorowego możemy napisać, że
153
dS = dp (1) × dp ( 2 ) .
W składowych (8.43) mamy zależność
dS k = ε kij dz i dz j
(1)
( 2)
= ε kij
∂z i ∂z j
dαdβ ,
∂α ∂β
(8.44)
która określa zorientowany element powierzchni. Dla powierzchni
zamkniętej parametryzację α , β dobieramy tak, aby wektor dS k był
skierowany na zewnątrz obszaru zamkniętego.
Pole dS powierzchni płata elementarnego jest równe długości
wektora dS k , tzn., że
1
2
dS = (dSk ⋅ dSk ) = (ε kijdzi dzj ε kmndzm dzn
(1)
(2)
(1)
∂zi ∂z j ∂zm ∂zn 12
) = (ε kijε kmn
) dαdβ.
∂α ∂β ∂α ∂β
1
(2) 2
Wykorzystując własność symbolu permutacyjnego (D.5)
ε kij ε kmn = δ im δ jn − δ in δ jm
pole dS możemy przedstawić w postaci
dS = (εkijεkmn
∂z ∂z j ∂zm ∂zn 12
∂zi ∂z j ∂zm ∂zn 12
) dα dβ. ={(δimδ jn −δinδ jm) i
} dα dβ =
∂α ∂β ∂α ∂β
∂α ∂β ∂α ∂β
∂zi ∂z j ∂zi ∂z j ∂zi ∂z j ∂z j ∂zi 12
} dα dβ ≡ A(α, β)dα dβ.
−
={
∂α ∂β ∂α ∂β ∂α ∂β ∂α ∂β
Całkowite pole płata jest zatem równe całce
∫ dS =
S
α2 β2
∫α β∫ A(α , β )dαdβ .
1
1
(8.45)
154
IIa. CAŁKA POWIERZCHNIOWA PO PŁACIE
NIEZORIENTOWANYM
Całką powierzchniową z pola tensorowego T o walencji q po płacie
niezorientowanym nazywamy całkę od tego pola po elemencie powierzchni
tego płata (8.45)
∫ TdS .
s
Całka ta, po wyborze układu współrzędnych, jest równoważna układowi
3 q całek podwójnych riemanowskich postaci
∫ Tijkl ...mn ( z p )dS =
S
α2 β2
∫α β∫ T
ijkl ... mn
1
( z p (α , β )) A(α , β )dαdβ .
(8.46)
1
Należy podkreślić, że w tym przypadku mamy tyle całek jaki jest wymiar
przestrzeni tensorów o walencji q, tzn. 3 q .
IIb. CAŁKA POWIERZCHNIOWA PO PŁACIE ZORIENTOWANYM
Całką powierzchniową z pola tensorowego T( P) o walencji q po
płacie zorientowanym nazywamy całkę powierzchniową postaci
∫ T ⊗ dS .
S
Po wyborze układu współrzędnych, całka ta jest równoważna układowi 3 q +1
całek podwójnych riemanowskich
∫ Tijkl...mn ( z p )dS r =
S
α2 β2
∫α β∫ T
ijkl ... mn
1
1
( z p (α , β ))ε rut
∂z u ∂z t
dαdβ .
∂α ∂β
(8.47)
Należy zauważyć, że w tym przypadku całek jest tyle jaki jest wymiar
przestrzeni tensorów rzędu q+1, tzn. tensorów o rząd wyższym niż pole
tensorowe całkowane T .
Dokonując zwężenia tensora T z elementem wektorowym płata dS
(8.44) uzyskujemy q różnych całek powierzchniowych
155
( µ , q +1)
~
∫ T ⊗ dS,
(1 ≤ µ ≤ q)
S
z których każda jest równoważna układowi 3 q −1 całek riemanowskich
podwójnych postaci
∫T
ijkl ...r ...mn
( z p )dS r =
S
α2 β2
∫ ∫T
α β
ijkl ...r ...mn
1
( z p (α , β ))ε rut
1
∂z u ∂z t
dαdβ .
∂α ∂β
(8.48)
Przykłady:
a) Całkę powierzchniową z pola wektorowego v (p) po powierzchni
zamkniętej postaci
∫ v(p) ⋅ dS = ∫ vk ( z p )dS k =
S
S
α2 β2
∫ ∫ vk ( z p (α , β ))ε kij
α 1 β1
∂z i ∂z j
dαdβ
∂α ∂β
nazywamy strumieniem wektora v przez powierzchnię.
b) Całkę powierzchniową z pola wektorowego v (p) po powierzchni
zamkniętej postaci
∫ v(p) × dS
S
nazywamy cyrkulacją wektora v po powierzchni zamkniętej. Jest ona
równoważna trzem całkom
∫ε
S
v dS j = ∫ ε kij vi n j dS .
kij i
S
III. CAŁKA OBJĘTOŚCIOWA
Obszarem regularnym V w przestrzeni fizycznej ε 3 nazywamy
obszar ograniczony skończoną liczbą płatów powierzchniowych S i
przecinających się wzdłuż krzywych regularnych Lk i zadany
156
parametrycznie jako funkcja od trzech zmiennych stanowiących
współrzędne krzywoliniowe w tym obszarze (równanie parametryczne
bryły)
p = p(α , β , γ )
lub w składowych
z k = z k (α , β , γ ) .
( α1 ≤ α ≤ α 2 , β 1 ≤ β ≤ β 2 , γ 1 ≤ γ ≤ γ 2 ).
Jeżeli przez dV oznaczymy elementarną objętość, to jest ona równa
wyznacznikowi z macierzy utworzonej ze składowych elementarnych
wektorów stycznych do linii układu krzywoliniowego.
Trzy wektory elementarne skierowane stycznie do krzywych α , β , γ
∂z k
∂z
∂z
( 2)
( 3)
dα ,
dz k = k dβ , dz k = k dγ
∂α
∂β
∂γ
są liniowo niezależne.
Elementarna objętość dV jest wówczas równa wyznacznikowi macierzy ze
składowych tych wektorów
dz k
(1)
dV = det( dz k
(1 )
=
, dz k
(2)
, dz k
( 3)
∂zk
∂z
∂z
dα , k dβ , k dγ ) =
∂α
∂β
∂γ
∂z ∂z ∂z
= det( k , k , k )dα dβ dγ
∂α ∂β ∂γ
) = det(
Jeżeli wprowadzimy oznaczenie
∂z ∂z ∂z
det( k , k , k ) = J (α , β , γ ),
∂α ∂β ∂γ
gdzie J (α , β , γ ) jest jakobianem przejścia od zmiennych z k do zmiennych
parametrycznych α , β , γ to otrzymujemy, że
dV = J (α , β , γ )dαdβdγ
(8.49)
i całkowitą objętość bryły wyznaczymy z całki potrójnej riemanowskiej
157
8.5. Twierdzenia całkowe
α2 β2 γ 3
∫ dV = α∫ β∫ γ∫ J (α , β , γ )dαdβdγ .
V
1
1 1
Całką objętościową z pola tensorowego T( P) rzędu q po objętości
V nazywamy całkę postaci
∫ TdV ,
V
która, po wyborze układu współrzędnych, jest równoważna układowi 3 q
całek riemanowskich potrójnych
∫T
ijkl ...mn
( z p )dV =
α2 β2 γ 2
∫ ∫ ∫T
ijkl ...mn
( z p (α , β , γ ) Jdαdβdγ .
(8.50)
α 1 β1 γ 1
V
Operacje całkowe na polach tensorowych można zatem sprowadzić do
całek pojedynczych, podwójnych i potrójnych przy założeniu ciągłości
funkcji podcałkowych.
W mechanice ośrodków ciągłych często korzysta się następujących
twierdzeń całkowych:
TWIERDZENIE 8.1
Twierdzenie Gaussa-Ostrogradskiego dotyczy przejścia od całki
objętościowej do całki powierzchniowej po powierzchni zamkniętej
ograniczającej daną objętość.
W tradycyjnej postaci twierdzenie to ma postać
∫ divvdV = ∫ v ⋅ ndS ,
V
S
(8.51)
( ∫ vi , i dV = ∫ vi ni dS )
V
S
gdzie n jest wersorem normalnej zewnętrznej do powierzchni S. Całkę tej
postaci nazywamy strumieniem wektora przez powierzchnię S .
Twierdzenie to można uogólnić i rozpatrzyć całkę z gradientu pola
wektorowego
158
∫ gradvdV = ∫ v ⊗ ndS
V
S
∫v ,
i j
V
dV = ∫ vi n j dS .
S
W mechanice ośrodków ciągłych interesują nas całki z dowolnych pól
tensorowych. Twierdzenie Gaussa-Ostrogradskiego można zastosować do
całek objętościowych z pola tensorowego. Niech T(P) będzie polem
tensorowym o walencji q. Twierdzenie Gaussa – Osrogradskiego ma
wówczas postać
∫ gradTdV = ∫ T ⊗ ndS = ∫ T ⊗ dS .
V
S
(8.52)
S
W wybranym układzie kartezjańskim jest to układ 3 q +1 całek (8.47)
∫T
, dV = ∫ Tijkl ...mp nr dS = ∫ Tijkl ...mp dS r .
ijkl .. mp r
V
S
S
Jako przypadki szczególne rozpatrujemy całki:
∫ gradϕdV = ∫ ϕndS ,
( ∫ ϕ , i dV = ∫ ϕni dS = ∫ ϕdS i )
∫ rotvdV = ∫ n × vdS ,
( ∫ ε ijk v k , j dV = ∫ ε ijk n j v k dS ).
V
V
S
S
V
V
S
S
S
Dla przypadku płaskiego wzór Gaussa-Ostrogradskiego przyjmuje postać
wzoru Greena, który dotyczy przejścia od całki powierzchniowej po
powierzchni płaskiej do całki krzywoliniowej po krzywej płaskiej
zamkniętej ograniczającej daną powierzchnię.
TWIERDZENIE 8.2
Twierdzenie Stokesa daje możliwość przejścia od całki
krzywoliniowej po krzywej przestrzennej zamkniętej do całki
powierzchniowej po powierzchni rozpiętej na tej krzywej. Dla całki z pola
prędkości wzór ten ma postać
159
∫ v ⋅ dp = ∫ n ⋅ rotvdS ,
L
( ∫ vi dz i = ∫ ni ⋅ (rotv ) i dS = ∫ ni ε i jk v k , j dS ). (8.53)
S
L
S
S
Całkę tej postaci nazywamy cyrkulacją pola wektorowego v po krzywej
L.
TOŻSAMOŚCI GREENA
Korzystając z twierdzenia Gaussa-Ostrogradskiego można pokazać, że
spełnione są dwie tożsamości – zwane pierwszą i drugą tożsamością
Greena.
PIERWSZA TOŻSAMOŚĆ GREENA ma postać
∫ ϕ∆ψdV = ∫ ϕ
V
S
∂ψ
dS − ∫ gradϕ ⋅ gradψdV
∂n
V
(8.54)
lub w zapisie indeksowym
∫ ϕψ ,
V
ii
dV = ∫ ϕ
S
∂ψ
dS − ∫ ϕ , iψ , i dV .
∂n
V
Lewą stronę tej tożsamości można przekształcić do postaci
∫ ϕψ ,
V
ii
dV = ∫ [(ϕψ , i ), i −ϕ , i ψ , i ]dV = ∫ (ϕψ , i ), i dV − ∫ ϕ , iψ , i dV .
V
V
V
Z twierdzenia Gaussa –Ostrogradskiego (8.52) wynika, że
∫ (ϕψ , ),
i
V
i
dV = ∫ ϕψ , i ni dS = ∫ ϕ
S
S
∂ψ
dS ,
∂n
(8.55)
∂ψ
określa prędkość zmiany pola skalarnego ψ
∂n
w kierunku normalnej zewnętrznej n do powierzchni S .
Po podstawieniu równości (8.55) w miejsce całki po objętości
w przekształconej lewej stronie tożsamości (8.54) otrzymujemy prawą
stronę pierwszej tożsamości Greena.
gdzie wielkość
160
DRUGA TOŻSAMOŚĆ GREENA jest konsekwencją pierwszej
tożsamości Greena i ma postać
∫ (ϕ∆ψ − ψ∆ϕ )dV = ∫ (ϕ
V
S
∂ψ
∂ϕ
−ψ
)dS .
∂n
∂n
(8.56)
Zamieniając w pierwszej tożsamości Greena (8.54) ϕ na ψ otrzymujemy
∂ϕ
∫ψ∆ϕdV = ∫ψ ∂n dS − ∫ gradϕ ⋅ gradψdV .
V
S
V
Po odjęciu stronami od pierwszej tożsamości Greena (8.54) ostatniej
równości otrzymujemy drugą tożsamość Greena.
Twierdzenia całkowe mają zastosowanie w mechanice ośrodków ciągłych
przy wyprowadzaniu lokalnych zasad zachowania.
Rozdział 9. Czasoprzestrzeń fizyki klasycznej
Definicja
Czasoprzestrzenią fizyki klasycznej nazywamy zbiór N , którego
elementami są zdarzenia ( P,t ) , pary uporządkowane (punkt, chwila).
Zbiór N otrzymujemy z iloczynu kartezjańskiego
N =ε 3 ×T
(9.1)
P ∈ ε 3 , t ∈ T ⇒ ( P,t ) ∈ N .
Przestrzeń euklidesowa punktowa ε 3 jest modelem matematycznym
przestrzeni fizycznej. Przestrzeń ε 3 nie jest przestrzenia liniową. Można
wprowadzić stowarzyszoną z ε 3 przestrzeń euklidesową wektorową ∋ 3 ,
która to jest przestrzenią liniową z iloczynem skalarnym (2.11). Należy
teraz zająć się osią czasu T .
9.1. Miary czasu
Czas, zgodnie z definicją podaną przez Newtona, biegnie w jednym
kierunku, stale i jednostajnie. Matematycznie pojęcie czasu można
wprowadzić odwzorowując oś czasu – zbiór T na oś liczb rzeczywistych
R [30].
Definicja
Miarą czasu nazywamy odwzorowanie
τ :T ×T → R ,
t1 , t 2 ∈ T ⇒ τ ( t1 , t 2 ) ∈ R ,
które spełnia następujące aksjomaty:
a)
Λ
t1 ,t 2 ∈T
τ (t1 , t 2 ) = −τ (t 2 , t1 ),
(9.2)
162
b)
Λ
t1 , t 2 ,t3∈T
c) Λ Λ
t∈T α∈R
τ (t1 , t 3 ) = τ (t1 , t 2 ) + τ (t 2 , t 3 ) ,
(9.3)
τ (0, t ) = α ∈ R .
Wartość τ (t1 , t 2 ) (9.2) nazywamy odstępem czasowym chwil t1 i t 2
w mierze τ .
Zbiór T , po wprowadzeniu miary τ , jest zbiorem uporządkowanym.
Chwilę t1 nazywamy wcześniejszą od chwili t 2
(t1 < t 2 ) , jeżeli
τ (t1 , t 2 ) > 0.
Miara czasu τ jest określona jednoznacznie, gdy zadana jest jej
wartość dla dwóch dowolnych chwil t1 , t 2 . Wielkość τ (t1 , t 2 ) nazywamy
wówczas wzorcem czasowym.
Dla zadanego τ , ustalając w zbiorze T chwilę początkową t 0 = 0 ,
mamy jednoznaczne określone odwzorowanie osi czasu T na oś liczb
rzeczywistych R .
Jeżeli odwzorowanie
τ0 :T →R
jest określone jako odwzorowanie
τ 0 (t ) ≡ τ (0, t ) = α ∈ R ,
(9.4)
wówczas każdej chwili t ∈ T przyporządkowana jest liczba α ∈ R i oś
czasu modelujemy osią liczb rzeczywistych. Takie przyporządkowanie jest
możliwe gdy została wybrana miara czasu τ i wybrano chwilę początkową
t0 .
Dwie dowolne miary czasu τ 1 i τ 2 związane są zależnością
τ 2 = βτ 1 ,
β ∈R .
Jeżeli β > 0 to miary czasu τ 1 i τ 2 mają jednakowy zwrot. Gdy β < 0 to
miary czasu τ 1 i τ 2 maja zwrot przeciwny.
163
9.2. Odległości zdarzeń
W mechanice ośrodków ciągłych postuluje się, że dowolny proces
dynamiczny odbywa się w pewnej chwili czasowej oraz w pewnym miejscu
przestrzeni fizycznej. Przestrzeń fizyczną modelujemy przestrzenią
euklidesową punktową ε 3 , zaś oś czasu T osią liczb rzeczywistych. W ten
sposób konstruujemy czasoprzestrzeń fizyki klasycznej N = ε 3 × T . Jest to
przestrzeń czterowymiarowa do której przestrzeń euklidesowa ε 3 i oś czasu
wchodzą na różnych warunkach.
Na zbiorze N można określić dwa następujące działania:
a) Dla dwóch dowolnych zdarzeń definiujemy ich odstęp czasowy.
b) Dla dwóch zdarzeń równoczesnych (zdarzeń o odstępie czasowym
równym zero) definiujemy odległość tych zdarzeń.
9.2. Odległości zdarzeń
Dwa dowolne zdarzenia na ogół różnią się miejscem zajmowanym
w przestrzeni fizycznej jak również chwilą w której dane zdarzenia
zachodzą. Przestrzeń fizyczna i oś czasu wchodzą do definicji
czasoprzestrzeni (9.1) w istotnie różny sposób. Na dowolnych zdarzeniach
można zdefiniować odwzorowanie zwane ich odstępem czasowym, zaś
odległość zdarzeń jest zdefiniowana jedynie dla zdarzeń równoczesnych.
ODSTĘP CZASOWY DWÓCH DOWOLNYCH ZDARZEŃ
Każdej dowolnej parze zdarzeń ( P, t1 ) ∈ N i (Q, t2 ) ∈ N
przyporządkowujemy liczbę
ϕ :N ×N →R ,
ϕ [( P, t1 ), (Q, t2 )] ≡ τ (t1 , t2 ) ∈ R ,
którą nazywamy ich odstępem czasowym.
(9.5)
164
Dwa zdarzenia ( P, t1 ) ∈ N i (Q, t2 ) ∈ N nazywamy równoczesnymi, jeżeli
t1 = t 2 , tzn., że odstęp czasowy tych zdarzeń τ (t1 , t 2 ) = τ (t1 , t1 ) = 0. Należą
one wówczas do podzbioru N t1 = ε 3 × {t1 } , który jest przekrojem czasowym
zbioru N . Są to zdarzenia, które zachodzą w tej samej chwili - w chwili t1 .
ODLEGŁOŚĆ ZDARZEŃ RÓWNOCZESNYCH
Każdej dowolnej parze zdarzeń równoczesnych
( P, t1 ) ∈ N t1
i (Q, t1 ) ∈ N t1 przyporządkowujemy wektor, którego długość nazywamy
odległością tych zdarzeń
→
ψ [( P, t1 ), (Q, t1 )] = PQ ∈ R .
(9.6)
Z podanych odwzorowań (9.5) i (9.6) wynika, że do zbioru N
przestrzeń euklidesowa i oś czasu wchodzą na różnych warunkach. Odstęp
czasowy został zdefiniowany dla dwóch dowolnych zdarzeń, zaś odległość
zdarzeń została zdefiniowana jedynie dla zdarzeń równoczesnych. Bardzo
istotną cechą zbioru N jest możliwość utożsamiania punktów w różnych
przekrojach czasowych. Dwa zdarzenia mogą zachodzić w tym samym
miejscu w przestrzeni euklidesowej, ale w różnych chwilach czasowych.
Jeżeli
( P, t1 ) ∈ N t1 , (Q, t2 ) ∈ N t 2 ,
to równość P = Q oznacza, że w tych zdarzeniach punkty te są w tym
samym miejscu w przestrzeni euklidesowej, ale w różnych chwilach
czasowych.
9.3. Automorfizmy czasoprzestrzeni
Można rozpatrywać odwzorowania czasoprzestrzeni N w siebie
W :N →N ,
W : ε3 ×T → ε3 ×T .
(9.7)
165
9. 3. Automorfizmy czasoprzestrzeni
Każde odwzorowanie iloczynu kartezjańskiego
dwóch odwzorowań:
U : ε3 ×T → ε3 ,
ε3 ×T
w siebie składa się z
(9.8)
V : ε3 ×T → T .
A zatem odwzorowanie (9.7)
W : ε3 ×T → ε3 ×T .
ma postać
W ( P, t ) = {U ( P, t ),V ( P, t )} .
(9.9)
W mechanice ośrodków ciągłych interesują nas automorfizmy
czasoprzestrzeni N . Są to odwzorowania (9.9) liniowe, odwracalne
czasoprzestrzeni N na siebie zachowujące strukturę czasoprzestrzeni.
Zachowują one zatem odstępy czasowe dowolnych zdarzeń (9.5)
i odległości zdarzeń równoczesnych (9.6).
Muszą być wówczas spełnione następujące warunki:
ϕ [W ( P, t1 ),W (Q, t 2 )] = ϕ [( P, t1 ), (Q, t 2 )] = τ (t1 , t 2 ).
(9.10)
→
ψ [W ( P, t1 ),W (Q, t1 )] = Lt ψ [( P, t1 ), (Q, t1 )] = PQ ,
1
gdzie przez Lt1 oznaczono automorfizm w
∋ 3 . Przy takim odwzorowaniu
zdarzenia równoczesne przechodzą w równoczesne i zachowana jest
odległość zdarzeń równoczesnych.
Z równości (9.9)
W ( P, t ) = {U ( P, t ),V ( P, t )}
wynika, że dla ustalonej chwili t odwzorowaniu U (P,t ) (9.8) można
przyporządkować odwzorowanie
U t : ε 3 × {t} → ε 3 .
(9.11)
166
Jest to jednoparametrowa rodzina odwzorowań zależna od parametru t.
Analogicznie, dla ustalonego punktu P odwzorowaniu V ( P, t ) można
przyporządkować odwzorowanie
VP : {P} × T → T .
(9.12)
Jest to również jednoparametrowa rodzina odwzorowań zależna od
parametru P .
Odwzorowanie (9.9) można wówczas przedstawić w postaci
W ( P, t ) = {U t ( P),VP (t )}.
(9.13)
Z zachowania odstępów czasowych wynika, że
τ (VP (t1 ),VQ (t 2 )) = τ (t1 , t 2 ) .
Odwzorowanie V P nie zależy zatem od punktu P.
Automorfizmami osi czasu T są więc przekształcenia postaci
V P (t ) = t ∗ = t + a ,
(9.14)
gdzie a ∈ R . Liczba a charakteryzuje automorfizm.
Z zachowania odległości zdarzeń równoczesnych wynika, że
→
→
U t ( P ), U t (Q ) = Q t ( PQ ) ,
(9.15)
gdzie tensor Q t jest tensorem ortogonalnym drugiego rzędu (4.2).
9.4. Obserwator przestrzeni i układ odniesienia
Aby podać postać automorfizmu czasoprzestrzeni N na siebie należy
podać definicję układu odniesienia oraz obserwatora, [30].
Mamy wprowadzić obiekt, który obserwuje przestrzeń euklidesową
punktową i związaną z nią algebrę tensorową. Minimalne ciało, które może
być obserwatorem składa się z czterech cząstek: χ 0 , χ 1 , χ 2 , χ 3. .
167
9. 4. Obserwator przestrzeni i układ odniesienia
Definicja
Obserwatorem O przestrzeni ε 3 nazywamy zbiór o czterech
uporządkowanych elementach { χ 0 , χ 1 , χ 2 , χ 3. }={ χ 0 ; χ i } -(najprostszy
sympleks w ε 3 ma cztery wierzchołki).
Klasę odwzorowań
κ : {χ 0 ; χ i } → ε 3 .
nazywamy konfiguracją κ obserwatora O w
cząstek na punkty w przestrzeni euklidesowej ε 3
P0 = κ ( χ 0 ),
ε 3 . Jest to odwzorowanie
Pi = κ ( χ i ).
(9.16)
Punkt P0 = κ ( χ 0 ) nazywamy umiejscowieniem obserwatora
konfiguracji κ .
Konfigurację κ nazywamy nieosobliwą, gdy wektory
→
→
κ ( χ 0 )κ ( χ i ) = P0 Pi ∈ ∋ 3
w
(9.17)
są liniowo niezależne.
Definicja
Układem odniesienia w ε 3 nazywamy każdą uporządkowaną czwórkę
punktów
{O; X i } i=1,2,3
→
(9.18)
taką, że wektory OX i = x i są liniowo niezależne. Punkt O nazywamy
początkiem układu odniesienia.
A zatem każda nieosobliwa konfiguracja obserwatora jest układem
odniesienia.
Układ odniesienia jest ortogonalny, gdy
→
→
OX i ⋅ OX j = 0 dla i ≠ j.
168
Z pojęciem układu odniesienia jest ściśle związane pojęcie repera w ε 3 .
Reperem w ε 3 nazywamy parę {P0 ; p i } złożoną z punktu P0 zaczepienia
repera i bazy pi ∈ ∋ 3 - trójki wektorów liniowo niezależnych.
→
Reper {P0 ; p i } , gdzie p i = P0 Pi nazywamy reperem układu odniesienia
{P0; Pi } , (9.16).
Biorąc układ odniesienia {P0 ; Pi } i jego reper {P0 ; p i } możemy dowolny
punkt X ∈ ε 3 przedstawić w postaci
→
P0 X = x = x i p i
(9.19)
X = P0 + x = P0 + x i p i .
(9.20)
lub w postaci symbolicznej
Ostatnia równość nie oznacza dodawania punktów i wektorów. Oznacza ona
jedynie, że punkt X jest końcem wektora x o początku w punkcie P0 .
Liczby x i nazywamy współrzędnymi punktu X w układzie odniesienia
{P0 ; Pi } .
Dwa układy odniesienia {P0 ; Pi } i {R0 ; Ri } o reperach {P0 ; p i }
→
→
i {R0 ; ri } , gdzie p i = P0 Pi i ri = R0 Ri mogą być dwiema różnymi
konfiguracjami tego samego obserwatora lub konfiguracjami dwóch
różnych obserwatorów.
Ruch obserwatora składa się zatem z przeniesienia go z punktu P0 do
punktu R0 oraz z liniowego odwzorowania wektorów p i w wektory ri przy
pomocy afinora A . Tym samym zmiana układu odniesienia określona jest
→
przez tensor A i wektor c = P0 R0 .
Wracając do automorfizmów w N zauważmy, że odwzorowanie (9.11)
U t : ε 3 × {t} → ε 3
ma zachowywać odległości zdarzeń równoczesnych (9.15)
9. 4. Obserwator przestrzeni i układ odniesienia
→
169
→
U t ( P ),U t (Q) = Q t ( PQ) .
Jeżeli przyjmiemy, że punkt P = O jest początkiem układu
odniesienia, zaś punkt X jest dowolnym punktem należącym do ε 3 , to
z (9.15) wynika, że
→
→
U t (O),U t ( X ) = Q t (OX ) .
(9.21)
Odwzorowanie U t (9.11) można przedstawić w postaci:
U t (0) = O + c ,
(9.22)
→
U t ( X ) = U t (O + x) = U t (O) + Q t (OX ) = O + c + Q t x ,
gdzie
X =O+x
→
co oznacza, że OX = x .
Jeżeli przyjmiemy następujące oznaczenie
U t (O + x) ≡ O + x ∗
to równość (9.22) można zapisać jako zależność
x∗ = Qt x + c .
na
(9.23)
Automorfizm N → N
(9.7) można traktować jako zmianę
obserwatora. Jeden obserwator widzi dane zdarzenie fizyczne w chwili t w
punkcie X - zdarzenie ( X , t ) . To samo zdarzenie inny obserwator widzi w
chwili t ∗ w punkcie X ∗ - zdarzenie ( X ∗ , t ∗ ) .
Zmiana obserwatora jest związana ze zmianą punktu w przestrzeni
euklidesowej punktowej ε 3 (wektora w ∋ 3 ) i z przesunięciem na osi czasu.
Jedno-jednoznaczna zależność między punktami w ε 3 a wektorami w ∋ 3
jest ustalona poprzez przyjęcie układu odniesienia. Ostatecznie automorfizm
czasoprzestrzeni N można przedstawić w postaci
170
x ∗ (t ∗ ) = Q(t )x(t ) + c(t ) ,
t∗ = t + a .
(9.24)
Jest to najbardziej ogólna jedno-jednoznaczna transformacja
czasoprzestrzeni N na siebie (9.7), która zachowuje :
• kolejność zdarzeń,
• odległość zdarzeń równoczesnych (odległość między dowolną parą
punktów w ε 3 ),
• odstępy czasowe dowolnych zdarzeń.
Należy odróżnić zmianę obserwatora od zmiany układu współrzędnych,
przy której zmieniają się jedynie współrzędne punktu. Sam punkt pozostaje
bez zmian.
Automorfizmy czasoprzestrzeni N na siebie są wykorzystywanie w
mechanice przy definiowaniu wielkości obiektywnych.
Dodatek
W mechanice ośrodków ciągłych przestrzeń fizyczną rozpatrujemy
jako przestrzeń euklidesową punktową P ∈ ε 3 , którą można zawsze
odwzorować w przestrzeń euklidesową wektorową ∋3 (po wyborze punktu
O∈
ε3
będącego
wektorową
∋3
→
początkiem promień wektora OP ), zaś przestrzeń
można odwzorować w przestrzeń liczbową R 3 = R × R × R
(po wyborze bazy ei w
∋3 ).
uporządkowanych układów
Przestrzeń R 3 jest zbiorem wszystkich
( x1 , x 2 , x 3 )
składających się z 3 liczb
→
rzeczywistych x1 , x 2 , x 3 ∈ R , OP = x1e1 + x 2e 2 + x 3e3 = x iei . Ostatnia
równość wynika z konwencji sumacyjnej Einsteina. Wektor jest zatem
obiektem geometrycznym jedno indeksowym w ustalonej bazie ei ,
→
OP = x ⇒ x i . W przestrzeni euklidesowej zawsze można wprowadzić bazę
ortonormalną i wówczas możemy pisać wszystkie indeksy na jednym
→
poziomie OP = xiei . W dalszym ciągu obowiązuje konwencja sumacyjna.
Baza ei jest ortonormalna, gdy
ei ⋅ e j = δ ij ,
gdzie δ ij jest deltą Kroneckera zdefiniowaną następująco:
dla i = j ,
(D.1)
dla i ≠ j.
Jest to wielkość dwu indeksowa, tak jak macierz kwadratowa
o wymiarze 3 × 3 . W zapisie macierzowym ma ona postać macierzy
diagonalnej
1 0 0
(δ ij ) =  0 1 0 .
(D.2)
0 0 1


1
δ ij = 
0
172
Dodatek
Poza deltą Kronekera, ważną rolę w mechanice ośrodków ciągłych
odgrywa wielkość trój indeksowa ε ijk , zwana symbolem permutacyjnym
albo alternatorem Levi-Civita`. Wielkość ta zdefiniowana jest następująco:
ε ijk
0

= + 1
− 1

.
(D.3)
Symbol ε ijk przyjmuje wartość 0 jeżeli i = j lub j = k lub k = i.
Przyjmuje on wartość +1 jeżeli ijk otrzymuje się z 123 w wyniku parzystej
liczbie przestawień (permutacji). Symbol ε ijk przyjmuje wartość -1
wówczas, gdy ijk otrzymuje się z 123 w wyniku nieparzystej liczbie
przestawień.
Symbol
permutacyjny
(D.3)
jest
wielkością
absolutnie
antysymetryczną, ponieważ
ε ijk = −ε jik = ε jki = −ε kji = ε kij = −ε ikj .
(D.4)
Dla symbolu permutacyjnego ε ijk (D.3) spełnione są następujące
równości:
ε ijk ε ijk = 6 ,
ε mjk ε njk = 2δ mn ,
ε ijk ε imn = δ jmδ kn − δ jnδ km .
(D.5)
Korzystając z własności symbolu ε ijk (D.4), wyznacznik dowolnej
macierzy kwadratowej
postaci:
( Amn )
o wymiarze 3 × 3 można przedstawić w
1
det ( Amn ) = ε ijk ε rst Air Ajs Akt
6
lub
173
Dodatek
ε ijk det ( Amn ) = ε rst Air A js Akt .
(D.6)
Symbol permutacyjny ε ijk można również wykorzystać do zapisu
objętości czworościanu rozpiętego na trzech wektorach liniowo
niezależnych u, v, w przez ich składowe w bazie ortonormalnej. Mamy
wówczas, że
V = ε ijk ui v j wk .
(D.7)
Jeżeli rozpatrujemy iloczyn wektorowy dwóch wektorów u i v
w = u× v ,
(D.8)
to łatwo udowodnić, że dla składowych tych wektorów w tej samej bazie
ortonormalnej spełniona jest równość
wi = ε ijk u j vk .
(D.9)
Z definicji symbolu ε ijk (D.3) wynika, że wi ⋅ ui = wi vi = 0 . A zatem
wektor w jest prostopadły do obu wektorów u i v .
Z drugiej strony, z (D.9) wynika, że
wi wi = ε ijk wiu j vk .
(D.10)
Lewa strona tej równości jest równa kwadratowi długości wektora w ,
2
ponieważ w = wi wi . Strona prawa, zgodnie ze wzorem (D.7), jest równa
objętości czworościanu rozpiętego na tych wektorach. Jest to iloczyn pola
podstawy i wysokości. Oznacza to, że iloczyn wektorowy jest wektorem,
którego długość jest równa polu równoległoboku rozpiętego na wektorach
u i v.
Tensory euklidesowe są elementami przestrzeni utworzonych
z przestrzeni euklidesowych wektorowych ∋3 . Przestrzeń tensorów rzędu p
(o walencji p) T p jest otrzymana z przestrzeni ∋3 w wyniku p-krotnego
iloczynu tensorowego
∋3 . A zatem mamy, że
174
Dodatek
T p =∋ 3
⊗
∋ 3 ⊗...⊗ ∋ 3 .
Tensory drugiego rzędu są więc elementami przestrzeni T 2 =∋ 3 ⊗ ∋ 3 .
Jeżeli tensor A ∈ T 2 , to w ustalonej bazie ortonormalnej ei można napisać,
że
A = Aij ei ⊗ e j .
(D.11)
Tensor drugiego rzędu A ∈ T 2 w ustalonej bazie można zatem
traktować jak wielkość dwu indeksową Aij . Podobnie można rozpatrywać
tensory o dowolnej walencji.
O rzędzie tensora będzie nas informowała liczba wolnych indeksów.
Wielkość Lijkl jest reprezentacją tensora czwartego rzędu, natomiast
wielkość Lijkk = Lij11 + Lij 22 + Lij 33 jest reprezentacją tensora drugiego rzędu.
W zapisie indeksowym w ustalonym układzie kartezjańskim
napisać.
Dla wektorów
x ⇔ xi ,
u ⋅ v ∈ R ⇔ ui vi ,
u ⊗ v ∈ T 2 ⇔ ui v j .
Dla tensorów
1 ⇔ δ ij .
A ⇔ Aij ,
możemy
(D.12)
(D.13)
L ⇔ Lijkl .
Dla tensorów drugiego rzędu można rozpatrywać następujące
operacje:
tr1 = δ ii = 3,
trA = Aii ∈ R ,
det A = det( Aij ) ∈ R ,
AT ∈ T2 ⇔ ( AT )ij = A ji ,
175
Dodatek
2
A = AA ∈ T 2
⇔
Aip Apj ,
A = A A ∈T 2
⇔
( A)ip Apj = Aim Amn ..... Asp Apj ,
1x = x
⇔
Ax = A ⋅ x ∈ T 1 = ∋ 3
δ ij x j = xi ,
⇔
Aij x j ,
⇔
yi Aij x j
⇔
Aij xk ,
AB ∈ T 2
⇔
Aip B pj ,
A ⋅ B ∈R
⇔
Aij Bij ,
A ⊗ B ∈T 4
⇔
Aij Bkl .
n
n −1
y ⋅ A ⋅ x = x ⋅ AT ⋅ y =
A ⋅ ( y ⊗ x ) ∈R
A ⊗ x ∈T 3
n
(D.14)
Jeżeli tensor drugiego rzędu spełnia warunek
⇔
QQT = QT Q = 1
QmiQmj = QimQ jm = δ ij ,
to taki tensor nazywamy tensorem ortogonalnym. Zachodzi wówczas
równość
−1
QT = Q .
Dla tensorów drugiego rzędu i tensorów czwartego rzędu można dokonać
następujących operacji:
L ⋅ A ∈T 2
⇔
Lijkl Akl ,
I ∈T 4
⇔
(I )ijkl = δ ikδ jl ,
I⋅A = A
⇔
δ ikδ jl Akl = Aij
A ⋅ L ∈T 2
⇔
Lijkl Aij ,
TrL ∈ R
⇔
Lijij ,
1 ⋅ L ⋅ 1 ∈R
⇔
Liijj ,
LT
⇔
(LT )ijkl = Lklij .
(D.15)
176
Dodatek
Gdy
L, H ∈ T 4 ,
to
L ⋅ H ∈R
⇔
Lijkl H ijkl ,
L o H ∈T 4
⇔
Lijmn H mnkl .
(D.16)
Symbol permutacyjny ε ijk (D.3) mimo, że jest wielkością
indeksową, nie jest reprezentacją tensora trzeciego rzędu.
Zgodnie z transformacyjną definicją tensora, tensor T rzędu
składowych Tij ......... mn w układzie {xm } , w innym układzie kartezjańskim
trój
p o
{~
xl }
związanym z {xm } zależnościami
~
x l = α lm xm
(D.17)
~
ma składowe Trs....tu , przy czym
~
Trs...tu = α riα sj ...α tmα unTij ...mn ,
(D.18)
gdzie macierz α lm jest macierzą ortogonalną.
Można pokazać, że symbol permutacyjny ε ijk podlega regułom
transformacji tensora (D.18) tylko dla transformacji reprezentujących obroty
układu, gdy det(α lm ) = +1 . Nie podlega tym regułom dla odbić, gdy
det(α lm ) = −1. Fakt ten wynika z definicji wyznacznika macierzy (D.6). Gdy
w (D.6) przyjmiemy, że Aij = α ij , to otrzymujemy wzór na transformację
symbolu permutacyjnego
ε ijk det (α mn ) = ε rstα irα jsα kt .
(D.19)
Obiekty geometryczne o tych własnościach nazywa się pseudotensorami.
I tak na przykład pseudoskalarem będzie wielkość (D.7), pseudowektorem
będzie iloczyn wektorowy dwóch wektorów (D.8). Pseudowektor
ui = ε ijk Ajk nazywamy wektorem dwoistym do tensora Ajk i zależy on tylko
od części antysymetrycznych tensora A . Mamy mianowicie, że
177
Dodatek
u1 = A23 − A32 , u2 = A31 − A13 , u3 = A12 − A21.
Wektor dwoisty do tensora symetrycznego jest wektorem zerowym.
Własność tę można uogólnić.
Niech T, S, W ∈ T 2 są trzema tensorami drugiego rzędu, wówczas
a) jeżeli T ⋅ S = Tij Sij = 0 dla każdego S , to tensor T = 0 (jest
tensorem zerowym),
b) jeżeli T ⋅ S = Tij Sij = 0 dla każdego S symetrycznego ( ST = S ), to
tensor T jest tensorem antysymetrycznym ( TT = −T ),
c) jeżeli T ⋅ W = TijWij = 0 dla każdego W antysymetrycznego
( WT = − W ), to tensor T jest symetryczny ( TT = T ).
Każdy tensor T ∈ T 2 możemy jednoznacznie przedstawić w postaci sumy
jego części symetrycznej i antysymetrycznej
T = T( s ) + T( a ) ,
gdzie
1
T( s ) = (T + TT ),
2
1
T( a ) = (T − TT ).
2
(D.20)
Wykorzystując podane powyżej fakty możemy napisać, że
T ⋅ S = (T( s ) + T( a ) ) ⋅ (S ( s ) + S ( a ) ) = T( s ) ⋅ S ( s ) + T( a ) ⋅ S ( a ) ,
(D.21)
ponieważ
T( s ) ⋅ S ( a ) = T( a ) ⋅ S ( s ) = 0 .
(D.22)
W mechanice ośrodków ciągłych z podanych własności korzysta się
przy dowodzie symetrii tensora naprężenia.
W mechanice ośrodków ciągłych korzysta się również z tak zwanego
twierdzenia o dzieleniu tensorów. Przy definiowaniu operacji na tensorach
nie zdefiniowaliśmy operacji dzielenia tensora przez tensor. Została
natomiast zdefiniowana operacja nasunięcia dwóch tensorów.
178
Dodatek
Jeżeli dane są dwa tensory L ∈ T 4 , A ∈ T 2 , to możliwe działania na
tych tensorach zostały podane w (D.14) i (D.15).
I tak w wyniku ich pełnego nasunięcia L ⋅ A otrzymujemy tensor rzędu dwa
( Lijkl Akl ). Wykorzystajmy tę własność.
Niech rozpatrywana przez nas fizyczna wielkość, w danym
prostokątnym układzie kartezjańskim, jest opisana układem 34 = 81 liczb
Lijkl . Zakładamy, że przy zmianie układu współrzędnych, wielkość Lijkl Akl
dla dowolnego tensora Akl transformuje się jak tensor drugiego rzędu.
Można wówczas pokazać, że liczby Lijkl są składowymi tensora czwartego
rzędu. Należy pokazać, że składowe te transformują się według wzoru
(D.18). Własność ta znana jest jako twierdzenie o dzieleniu tensorów.
Korzysta się z niej przy dowodzie, że gradϕ = v (gradient skalara jest
wektorem), gradv = A (gradient wektora jest tensorem drugiego rzędu).
Literatura
1. R. Abraham, J. E. Marsden, T. Rating, Manifolds, Tensor Analysis, and
Application, Springer-Verlag, New York 1988, (second Edition).
2. L. Auslander, R. E. Mac Kenzie, Rozmaitości różniczkowalne, PWN,
Warszawa 1969.
3. E. Beltrami, Sulla condizioni di resistenza dei corpi elastici, Rend. I-st.
Lomb. II, 18, 1885.
4. A. Blinowski, Obroty ciał odkształcalnych, część I, Geometria
i kinematyka, 7/1994, Prace IPPT.
5. W. T. Burzyński, Studium nad hipotezami wytężenia , Lwów 1928, lub
Dzieła Wybrane, t. I, PWN, Warszawa 1982.
6. S. C. Cowin and M. M. Mehrabadi, On the identification of material
symmetry for anisotropic elastic materials, Quart. J. Mech. Appl. Math.
40, 451-476, 1987.
7. K. F. Czernych, Vviedienije w anizotropnuju uprugost, Izd „Nauka”
Moskva 1988, (w języku rosyjskim).
8. I. M. Gelfand, Lekcii po linejnoj algebre, Izd.“Nauka” Moskwa 1996,
wydanie trzecie (w języku rosyjskim).
9. S. Gołąb, Rachunek tensorowy, PWN, Warszawa 1966 (wydanie
drugie).
10. H. Hencky, Zur Theorie plastischer Deformationen und der hierdurch
im Material hervorgerufenen Nachspannungen, ZAMM, 4, 323-334,
1924.
180
Literatura
11. M. T. Huber, Właściwa praca odkształcenia jako miara wytężenia
materiału, Czas. Techn. XXII, Lwów 1904.
12. N. Je, Koczin, Wjektornoje isczislenije i naczała
tenzornogo
isczislenija, Izd. „Nauka” Moskva 1965, (w języku rosyjskim) wydanie
dziewiąte.
13. J. Komorowski, Od liczb zespolonych do tensorów, spinorów, algebr
Liego i kwadratyk, PWN, Warszawa 1978.
14. K. Kowalczyk-Gajewska, J. Ostrowska-Maciejewska, The influence of
internal restrictions on the elastic properties of anisotropic materials,
Arch. Mech., 56, 3, 205-232, Warszawa 2004.
15. K. Kuratowski, Topologia, PWN, Warszawa 1966.
16. H. Lass, Vector and Tensor Analysis, McGraw-Hill Book Company,
INC, 1950.
17. S.G. Lechnickij, Tieorija uprugosti anizotropnogo cieła, Gosudar. Izd. ,
Moskva, 1950, (w języku rosyjskim).
18. G, Ja. Ljubarskij, Tieorja grup i je primjenienije w fizykje, Gosudar. Izd.
Fizyko-Mat. Literatury, Moskva 1958, (w języku rosyjskim).
19. J.C. Maxwell, Origins of Clerk Maxwell`s electric ideas as descibed in
familiar letters to William Thomson, Cambridge at the University Press
1937, (in the letter from 1856), Proc. Cambridge Phil. Soc., 32, 1936.
20. A.J. Mc Connell, Application of tensor analysis, Dover Publications,
INC. New York 1957.
21. R. von Mises, Mechanik der festen Korper im plastisch deformablen
Zustand, Nachrichten der Koniglichen Gesellschaft der Wissenschaften
zu Gottingen, Math-Phys., 1, 4, 582-592, 1913.
181
Literatura
22. R. von Mises, Mechanik der plastischen Forman derung von Kristallen,
Zeitschrift fur Angewandte Mathematik und Mechanik, 8, 161-185,
1928.
23. A. Mostowski, M. Stark, Algebra Wyższa, część II, Warszawa, 1954.
24. J. Ostrowska-Maciejewska, Podstawy Mechaniki Ośrodków Ciągłych,
PWN, Warszawa 1982.
25. J. Ostrowska-Maciejewska, Mechanika Ciał Odkształcalnych, PWN,
IPPT PAN, Warszawa 1994.
26. B.I. Pobiedria, Lekcji po tenzornomu analizu, Izd. Moskovskovo
Universiteta 1974, (w języku rosyjskim).
27. H. Rasiowa, Wstęp do matematyki współczesnej, Warszawa 1977,
wydanie szóste.
28. P. K. Raszewskij, Rimanova geometria i tenzornyj analiz, Izd. „Nauka”
29. A. P. Robertson, W. Robertson, Topological Vector Spaces, Cambridge
University Press !964.
30. J. Rychlewski, Tensory i funkcje tensorowe, Biuletyn nr 631, Instytut
Maszyn Przepływowych PAN, Gdańsk 1969.
31. J. Rychlewski,
Matematyczeskaja
struktura
uprugich
tieł
”ceiiinosssttuv”, Raport 217, Inst. Probl. Mechaniki AN SSSR, Moskwa
1983 (w języku rosyjskim).
32. J. Rychlewski, PMM, 48 (1984) , 420-432, (w języku rosyjskim).
33. J. Rychlewski, Elastic energy decomposition and limit criteria,
Advances in Mechanics, 7, 3. 1984 (w języku rosyjskim).
34. J. Rychlewski, Symetria przyczyn i skutków, PWN, Warszawa 1991.
182
Literatura
35. J. Rychlewski, Unconventional approach to linear elasticity, Arch.
Mech., 47 (2), 159-171, Warszawa 1995.
36. J. Rychlewski, Anisotropy and proper states of materials, IUTAM
Symposium on Anisotropy, Inhomogeneity and Nonlinearity in Solids
mechanics, 19-24, 1995.
37. J. A. Schouten, “Tensor analysis for physicists”, Oxford 1951.
38. L. I. Siedov, Vviedienie w mechaniku splosznoj sredy, Fiz-Mat, Moskwa
1970, (w języku rosyjskim).
39. Ju. I. Sirotin, M. P. Szaskolskaja, Osnowy kristallofiziki, Izd. „Nauka”
40. I. S. Sokolnikoff, Tensor Analysis: Theory and Aplications, John Wiley
and Sons, Inc., New York 1951.
41. A. J. M. Spencer , Theory of Invariants, Continuum Phisics, vol.I New
York, Londyn 1971.
42. S. Sutcliffe, Spectral Decomposition of the Elasticity Tensor, Transactions of the ASME 762, vol. 59. December 1992.
43. J. L. Synge and A. Schild, Rachunek Tensorowy, PWN, Warszawa 1964.
44. W. Thomson (Lord Kelvin), On six principal strains of an elastic solids,
Phil. Trans. R. Soc., 166, (1856), 495-498.
45. T.C.T. Ting, Invariants of anisotropic elastic constants, The Quarterly
Journal of Mechanics and Applied Mathematics, 40, 431-448, 1987.
Skorowidz
afinor 43
automorfizm 24, 55, 59, 164
baza fizyczna 133
baza izometryczna 64
baza lokalna 21, 132, 144
ciało 19, 20
ciało materialne 10
delta Kroneckerà 23, 29, 171
dewiator 40, 52
diada 33
drugi indeks strukturalny 84
dystrybutory 83, 85
dywergencja pola tensorowego 139, 142, 143
efekt Kelvina 118, 120
efekt Poyntinga 119
endomorfizm 24
energetyczne stany własne 87, 98
energia sprężysta 91, 92, 93
forma liniowa 25
fundamentalna tożsamość dla operatora liniowego 47, 73, 77
funkcje tensorowe 107
- - hemitropowe 110
- - izotropowe 110
- - potencjalne 121
główny wzór strukturalny liniowej teorii sprężystości 78
gradient pola wektorowego 138
gradient pola tensorowego 137, 142
grupa abelowa 18
-symetrii funkcji 110
- - tensora 62, 63, 64, 69, 103
- - zbioru tensorów 63, 104
hipoteza ciągłości 10
iloczyn kartezjański 13
- skalarny 27, 41
- - energetyczny 93
- prosty 65
184
- tensorowy 27
- wektorowy 173
inwersja 57
izomer 44
izomorfizm 24, 46
konwencja sumacyjna Einsteina 21
kwadrat logiczny 15
miara czasu 161
moduły Kelvina 75, 79, 83
moduły Young’a 86
nierówność Schwartza 28
obserwator 166
odległość zdarzeń równoczesnych 164
odstęp czasowy 163, 164
operator nabla 141, 145
operatory liniowe 24, 42, 71
parametr Lode`go 120
pierwszy indeks strukturalny 82
pochodna kowariantna 148
pole wektorowe bezwirowe 140
- - bezźródłowe 140
- - nierozbieżne 140
- - potencjalne 140
- - solonoidalne 140
polibaza prosta 34, 36
potęga tensora 47
prawa de Morgana 13
projektor 52, 76, 89, 100
przestrzeń euklidesowa punktowa 17, 31
- - wektorowa 17, 27
- fizyczna 10, 17
- inwariantna 50, 75
- liniowa 20
- sprzężona 21
- własna 50, 75
pseudotensor 176
rotacja pola wektorowego 139, 143
rotacja pola tensorowego 143
Skorowidz
Skorowidz
równanie charakterystyczne 49, 79
stan bezpieczny 88
suma prosta 13, 26
symbole Christoffela 146, 147
symbol permutacyjny 172
ślad tensora 40, 47
tensor jednostkowy 43, 46, 73
- metryczny 35, 133
- nieosobliwy 46
- obrotu 56
- odbicia 57
- odwrotny 46
- ortogonalny 55, 175
- podatności 69
- rozkładalny 33, 36
- stanu granicznego 68, 87, 97
- sztywności 68
tensorowy trójmian kwadratowy 117
tensory izotropowe 62, 76
tensory zgodne 68, 102
twierdzenie Cayleyà-Hamiltona 52, 81
- Gaussa-Ostrogradskiego 157
- Greena 158
- o postaci ogólnej automorfizmu czasoprzestrzeni 169
- o reprezentacji odwzorowania liniowego 42
- o rozkładzie biegunowym (polarnym) tensora 58
- o rozkładzie spektralnym (widmowym) tensora 49, 53, 74, 94, 99, 100
- Stokesa 158
układ odniesienia 126, 167
wektor dwoisty do tensora 139, 176
wyznacznik Vandermonda 81
wzór Sylwestra-Lagrangeà 116
Zasady Curie 111
185

Podstawy i zastosowania rachunku tensorowego

Transkrypt

Podobne dokumenty

Rachunek Tensorowy

Pobierz PDF

Spis lektur

Gastronomia polityczna kuchmistrza litewskiego Michał Wielhorski