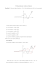Regionalne Koło Matematyczne

Regionalne Koło Matematyczne
Uniwersytet Mikołaja Kopernika w Toruniu
Wydział Matematyki i Informatyki
http://www.mat.umk.pl/rkm/
Lista rozwiązań zadań nr 18, grupa zaawansowana (13.03.2010)
O izometriach (c.d.)
Wektorem uporządkowanej pary prostych równoległych (a, b) nazywamy wektor ~u
równy wektorowi, którego początek znajduje się na prostej a, a koniec na prostej b
−→
oraz wektor ten jest prostopadły do prostych a, b. Wektor ten oznaczamy (a, b).
Translacją (przesunięciem) o wektor ~u nazywamy przekształcenie, które punktowi
−−→
X ∈ P przyporządkowuje taki punkt X ′ , że XX ′ = ~u. Translację oznaczamy symbolem Tu~ .
1. Niech a, b, c będą prostymi równoległymi. Pokazać, że Sc ◦ Sb ◦ Sa jest symetrią
osiową.
Rozwiązanie. Niech d będzie taką prostą równoległą do prostych a, b, c, że
−→
−→
(a, b) = (d, c). Wówczas
Sc ◦ Sb ◦ Sa = Sc ◦ (Sb ◦ Sa ) = Sc ◦ (Sc ◦ Sd ) = (Sc ◦ Sc ) ◦ Sd = Sd .
Zatem istotnie złożenie trzech symetrii osiowych o osiach równoległych jest
symetrią osiową. Na rysunku przedstawione jest położenie osi d.
c
d
~u
~u
a
b
1
Obrotem o środku O i kącie α nazywamy przekształcenie, które dowolnemu
punktowi X przyporządkowuje punkt X ′ taki, że |OX| = |OX ′| i |∠XOX ′| = α i
α
oznaczamy symbolem RO
. Oczywiście posługujemy się kątami skierowanymi.
2. Udowodnić, że Sb ◦Sa , gdy a ∦ b, jest obrotem wokół punktu przecięcia prostych
a i b o kąt, który jest dwa razy większy od kąta pary prostych.
Rozwiązanie. Uzasadnienie jest niemal identyczne, jak w sytuacji prostych
równoległych.
Niech proste a i b przecinają się w punkcie O. Weźmy dowolny punkt X i
dokonajmy przekształcenia Sb ◦ Sa na X. Niech X1 = Sa (X) i
X ′ = Sb (X1 ) = Sb ◦ Sa (X).
b
a
X1
X′
X
O
Łatwo zauważyć, że |OX| = |OX1| = |OX ′| oraz |∠XOX ′| = 2 · |∠(a, b)|.
W podobny sposób jak dla translacji dowodzimy, że
3. Każdy obrót można przedstawić jako złożenie dwóch symetrii osiowych.
4. Zbadać, jakim przekształceniem jest złożenie dwóch obrotów.
β
α
Rozwiązanie. Niech dane będą obroty RO
i RO
.
1
2
β
α+β
α
1. Jeśli O1 = O2 , to łatwo zauważamy, że RO
◦ RO
= RO
.
2
1
1
2. Niech O1 6= O2 .
Wówczas obroty przedstawiamy jako złożenia par dwóch symetrii osiowych. Niech b będzie prostą przechodzącą przez środki obrotów O1 , O2.
Proste a i c dobieramy tak, by ∠(a, b) = 12 α i ∠(b, c) = 12 β.
2
O
1
2β
1
2α
d
1
2β
b
1
2α
O1
O2
c
a
Wówczas
β
α
RO
◦ RO
= (Sc ◦ Sb ) ◦ (Sb ◦ Sa ) = Sc ◦ (Sb ◦ Sb ) ◦ Sa = Sc ◦ Sa .
2
1
Mogą zajść dwa przypadki.
2.1. a 6k c
2.2. a k c
W przypadku 2.1. niech O będzie punktem przecięcia prostych a i c. Przez
punkt O prowadzimy prostą d równoległą do b. Wówczas
1
1
1
∠(a, c) = ∠(a, d) + ∠(d, c) = α + β = (α + β).
2
2
2
β
α+β
α
Zatem RO
◦ RO
= RO
jest obrotem wokół punktu O o kąt α + β.
2
1
W przypadku 2.2. proste a i c są równoległe (patrz rysunek).
c
b
a
1
2β
1
2β
O1 1 α
2
O2
Zatem ∠(b, a) = 12 β. Stąd 12 α + 12 β = kπ i dalej
α + β = 2kπ.
β
β
α
α
Ponieważ RO
◦ RO
= Sc ◦ Sa i a k c, to RO
◦ RO
jest translacją.
2
2
1
1
Podsumowując mamy, że złożenie dwóch obrotów jest:
1) obrotem o kąt α + β, gdy środki obrotów się pokrywają,
3
2) obrotem o kąt α + β, gdy α + β nie jest całkowitą wielokrotnością kąta
pełnego,
3) translacją, gdy α + β jest całkowitą wielokrotnością kąta pełnego.
5. Jeśli proste a, b, c przecinają się w punkcie O, to Sc ◦Sb ◦Sa jest symetrią osiową.
Rozwiązanie. Dowód jest identyczny jak dla translacji, korzystamy z faktu, że
Sy ◦ Sx = Sz ◦ St wtedy i tylko wtedy, gdy ∠(x, y) = ∠(t, z).
6. Dany jest punkt P0 i trójkąt ABC. Niech P1 będzie obrazem punktu P0 w
obrocie wokół punktu A o kąt 120◦ . Punkt P2 jest obrazem punktu P1 w obrocie
dookoła punktu B o kąt 120◦, zaś punkt P3 jest obrazem punktu P2 w obrocie
dookoła punktu C o kąt 120◦ . Punkt P4 jest obrazem punktu P3 w obrocie
dookoła punktu A o kąt 120◦ , itd. Udowodnić, że jeżeli P2010 = P0 , to trójkąt
ABC jest równoboczny.
C
P0
A
B
Rozwiązanie. Wyznaczamy kolejno punkty P1 , P2 , P3 , . . . , P2010 w zależności
od punktu P0 .
Zatem
◦
120
P1 = RA
(P0 ),
◦
◦
◦
120
120
120
P2 = RB
(P1 ) = RB
◦ RA
(P0 ).
◦
◦
120
120
Przekształcenie RB
◦ RA
jest pewnym obrotem o 240◦ . Dalej
◦
◦
◦
◦
120
120
(P0 ) = Tu~ (P0 ).
P3 = RC120 (P2 ) = RC120 ◦ RB
◦ RA
{z
|
}
translacja
◦
◦
◦
120
120
Przekształcenie RC120 ◦ RB
◦ RA
jest przesunięciem o pewien wektor ~u.
Wówczas
◦
◦
◦
120
120
P6 = RC120 ◦ RB
◦ RA
(P3 ) = Tu~ (P3 ) = Tu~ (Tu~ (P0 )) = T2~u (P0 ).
Indukcyjnie dowodzimy, że
P3n = Tn~u (P0 ).
−−−−→
−
→
Zatem P2010 = T670~u (P0 ). Ponieważ P2010 = P0 , więc P0 P2010 = 0 = 670~u, to
−
→
~u = 0 .
◦
◦
120
Zatem Tu~ jest tożsamością. Tożsamością jest więc przekształcenie RC120 ◦RB
◦
◦
◦
◦
◦
−120
120
120
120
RA = 1P . Zatem RB ◦ RA = RC
.
Przedstawmy obroty w postaci złożenia symetrii osiowych.
4
c
C1
b
60◦
B
A
60◦
a
Mamy więc
◦
◦
◦
120
120
RB
◦ RA
= (Sc ◦ Sb ) ◦ (Sb ◦ Sa ) = Sc ◦ Sa = RC240
.
1
◦
◦
Ponieważ RC120 ◦ RC240
= 1P , to C = C1 . Na rysunku widzimy, że trójkąt ABC
1
ma kąty wewnętrzne o mierze 60◦ , co dowodzi, że trójkąt jest równoboczny.
7. Opisać izometrię, która jest złożeniem trzech symetrii osiowych.
Rozwiązanie. Przekształcenie Sa ◦ Tu~ , gdzie a jest prostą i wektor ~u k a, nazywamy symetrią z poślizgiem. Zauważmy, że jeśli ~u k a, to Sa ◦ Tu~ = Tu~ ◦ Sa .
1. Jeśli proste a, b, c są współpękowe, to Sc ◦ Sb ◦ Sa jest symetrią osiową.
Ten fakt wynika z poprzednich zadań.
2. Niech a, b, c będą prostymi nienależącymi do jednego pęku. Wówczas
mogą zajść następujące przypadki.
2.1.
2.2.
2.3.
2.4.
a k b i c 6k a,
a 6k b i c k a,
a 6k b i c k b,
a 6k b, c 6k b i c 6k a.
Ad. 2.1. Na rysunku mamy przedstawioną graficznie sytuację.
c
b
a
Zauważmy, że Sb Sa = Tu~ , więc
Sc ◦ Sb ◦ Sa = Sc ◦ Tu~ .
Ad. 2.2. Podobnie mamy wówczas
Sc ◦ Sb ◦ Sa = Sc ◦ Sa ◦ Sa ◦ Sb ◦ Sa = (Sc ◦ Sa ) ◦ (Sa ◦ Sb ◦ Sa ).
5
b
c
a
Ponieważ c k a, to istnieje wektor ~v taki, że Sc ◦Sa = T~v . Ponadto Sa ◦Sb ◦Sa =
Sd , gdyż proste a, b, a należą do jednego pęku. Zatem
Sc ◦ Sb ◦ Sa = T~v ◦ Sd .
Ad. 2.3. Tu mamy równość
Sc ◦ Sb ◦ Sa = (Sc ◦ Sb ) ◦ Sa = Tu~ ◦ Sa .
b
c
a
Ad. 2.4. Prowadzimy prostą d równoległą do c przez punkt przecięcia
prostych a i b.
b
c
d
a
Wówczas
Sc ◦ Sb ◦ Sa = (Sc ◦ Sd ) ◦ (Sd ◦ Sb ◦ Sa ) = Tu~ ◦ Sp ,
gdyż Sc ◦ Sd jest translacją, bo c k d, a Sd ◦ Sb ◦ Sa jest symetrią osiową.
Pozostaje nam opisać izometrie postaci Tu~ ◦ Sd i Sd ◦ Tu~ . Uczynimy to w przypadku Tu~ ◦ Sd , drugi przypadek opisujemy analogicznie. Na rysunku mamy
schemat naszej sytuacji.
6
~u
~v
w
~
d
Weźmy wektory ~v i w
~ takie, że
~v k d, w
~ ⊥ d i ~u = ~v + w.
~
Wówczas
Tu~ ◦ Sd = T~v+w~ ◦ Sd = T~v ◦ Tw~ ◦ Sd = T~v ◦ (Tw~ ◦ Sd ).
Translację Tw~ można przedstawić jako Sm ◦Sn , przy czym w
~ ⊥ m i m k n. Zatem
Tu~ ◦ Sd = T~v ◦ (Sm ◦ Sn ◦ Sd ).
Ponieważ m ⊥ w
~ iw
~ ⊥ d, to m k d, więc proste m, n, d są równoległe. Izometria
Sm ◦Sn ◦Sd jest więc symetrią osiową o osi r, która jest równoległa do prostych
m, n, d. Mamy więc
Tu~ ◦ Sd = T~v ◦ Sr .
Na zakończenie zauważmy, że ~v k r, gdyż ~v k d i r k d. Uwodniliśmy więc, że
izometria Sc ◦ Sb ◦ Sa jest symetrią z poślizgiem.
Wniosek. Dla dowolnych prostych a, b, c złożenie symetrii osiowych Sc ◦Sb ◦Sa
jest symetrią z poślizgiem.
7