Logika i teoria mnogo´sci - prz

Politechnika Rzeszowska
Katedra Informatyki i Automatyki
Krzysztof Wiktorowicz
Logika i teoria mnogości
Zadania i ćwiczenia laboratoryjne
Rzeszów 2009
Literatura
1. Literatura podstawowa:
• Rasiowa H., Wstep
˛ do matematyki współczesnej, PWN, Warszawa 2003.
• Marek W., Onyszkiewicz J., Elementy logiki i teorii mnogo´sci w zadaniach, PWN, Warszawa 2003.
• Trzesicki
˛
K., Logika i teoria mnogo´sci, EXIT, Warszawa 2003.
• Ben-Ari M., Logika matematyczna w informatyce, WNT, Warszawa 2005.
• Clocksin W. F., Mellish C. S, Prolog. Programowanie, Helion, Gliwice, 2003.
2. Literatura dodatkowa:
• Stanosz B., Wprowadzenie do logiki formalnej, PWN, Warszawa 2002.
• Stanosz B., Ćwiczenia z logiki, PWN, Warszawa 2002.
• Mostowski A., Logika matematyczna, http://matwbn.icm.edu.pl/ksspis.php?wyd=10.
• Kuratowski C., Mostowski A., Teoria mnogo´sci, http://matwbn.icm.edu.pl/ksspis.php?wyd=10.
Oprogramowanie
1. Programator sterownika SIEMENS LOGO! Soft Comfort:
• strona WWW: http://www2.automation.siemens.com/logo/index_76.html,
• link: Updates & Demo software,
• wersja: Download LOGO! Soft Comfort demo version V5.0.
2. Interpreter jezyka
˛
SWI-Prolog:
• strona domowa SWI-Prolog: www.swi-prolog.org,
• linki: Download | Stable release,
• wersja: SWI-Prolog/XPCE for MS-Windows.
Uwaga: Na mojej stronie domowej
prz-rzeszow.pl/~kwiktor
znajduja˛ sie˛ linki do wymienionego oprogramowania.
2
Ćwiczenie 1
Formuły i funktory zdaniotwórcze.
Równoważność logiczna. Funkcjonalna
pełność. Postacie normalne
1.1
Zadania teoretyczne
1.1.1
Formuły i funktory zdaniotwórcze
1. Zapisać formuły zdań. W każdym przypadku opisać atomy.
(a) Jeżeli nie spróbuje,
˛ to nie wygram.
Rozwiazanie:
˛
∼ p ⇒ ∼ q,
p – spróbuje,
˛ q – wygram.
(b) Nie jest prawda,˛ że jeżeli spróbuje,
˛ to wygram.
Rozwiazanie:
˛
∼ (p ⇒ q),
p – spróbuje,
˛ q – wygram.
(c) Jeżeli Adam o´swiadczył sie˛ Karolinie, to jest ´slepy lub zakochany.
Rozwiazanie:
˛
p ⇒ (q ∨ r),
p – Adam o´swiadczył sie,
˛ q – Adam jest ´slepy, r – Adam jest zakochany.
(d) Karolina przyjmie o´swiadczyny Adama i wyjdzie za niego, wtedy i tylko wtedy, gdy Adam zapisze jej
dom lub podaruje dwa samochody.
Rozwiazanie:
˛
(p ∧ q) ⇔ (r ∨ s), p – Karolina przyjmie o´swiadczyny Adama, q – Karolina wyjdzie za
Adama, r – Adam zapisze Karolinie dom, s – Adam podaruje Karolinie dwa samochody.
(e) Alfred czy´sci rewolwer i obmy´sla plan zemsty.
(f) Je´sli Roman wygra wybory, to Adam straci prace.
˛
(g) Karol zostanie ministrem lub konsulem.
(h) Sufit jest biały, a ´sciany sa˛ kolorowe.
(i) Poziom nie jest wysoki.
(j) Albo ja przyjde,
˛ albo ty przyjdziesz.
(k) O ile przeczytam podrecznik
˛
lub bed
˛ e˛ chodził na wykłady, to zdam egzamin.
(l) Nieprawda, że jeżeli skocze,
˛ to złamie˛ noge.
˛
(m) Je´sli spotkam kolegów, to o ile nie bedzie
˛
za pó´zno, to pójdziemy do kina.
(n) Nie jest prawda,˛ że je´sli skończe˛ studia i kurs jezykowy,
˛
to znajde˛ prace.
˛
(o) Wynik jest dobry, jeżeli jest wiekszy
˛
od 12 i nie przekracza 15.
2. Dla jakich wartości logicznych p i q podane formuły sa˛ prawdziwe.
(a) p ∧ q
Rozwiazanie:
˛
w (p) = 1, w (q) = 1.
(b) (p ∧ q) ⇒ 0
(c) (p ∨ q) ⇒ 0
(d) (p ∧ ∼ q) ⇒ p
3
1.1.2
Równoważność logiczna
1. Uprościć formuły dla w (p) = 1, a nastepnie
˛
dla w (p) = 0.
(a) (p ∨ ∼ q) ∧ q
Rozwiazanie:
˛
• dla w (p) = 1,
(p ∨ ∼ q) ∧ q ≡ (1 ∨ ∼ q) ∧ q ≡ 1 ∧ q ≡ q
• dla w (p) = 0,
(p ∨ ∼ q) ∧ q ≡ (0 ∨ ∼ q) ∧ q ≡ ∼ q ∧ q ≡ 0
(b) p ∨ q
(c) p ⇒ q
(d) p ⇔ q
(e) p ∨ ∼ p
(f) (p ∧ q) ⇒ p
(g) (p ∧ q) ⇔ p
(h) p ∧ ∼ (p ∨ q)
(i) p ⇔ (∼ p ∧ q)
(j) (∼ p ⇒ q) ⇒ ∼ p
(k) (p ⇔ ∼ p) ∨ (q ⇒ p)
1.1.3
Funkcjonalna pełność
1. Zdefiniować funktory. Odpowiedź uzasadnić używajac
˛ tabel wartości logicznych.
(a) ∼ za pomoca˛ {|}
Rozwiazanie:
˛
∼ p ≡ p | p.
(b) ∨ za pomoca˛ {|}
Rozwiazanie:
˛
p ∨ q ≡ ∼ (∼ p ∧ ∼ q) ≡ (∼ p) | (∼ q) ≡ (p | p) | (q | q)
(c) ∧ za pomoca˛ {∨, ∼}
(d) ∨ za pomoca˛ {∧, ∼}
(e) ∨ za pomoca˛ {⇒, ∼}
(f) ⇒ za pomoca˛ {|}
(g) ∨ za pomoca˛ {↓}
1.1.4
Postacie normalne
1. Zapisać równoważność p ⇔ q w dysjunkcyjnej i koniunkcyjnej postaci normalnej.
Rozwiazanie:
˛
dpn: (∼ p ∧ ∼ q) ∨ (p ∧ q),
kpn: (∼ p ∨ q) ∧ (∼ q ∨ p).
2. Podane formuły przedstawić w dysjunkcyjnej i koniunkcyjnej postaci normalnej.
(a) p ∧ [q ∨ (∼ p ∧ r)]
(b) (p ∨ q) ⇒ (q ∨ r)
(c) (p ∧ q) ⇒ (q ∧ p)
(d) (p ∧ q) ⇔ p
4
1.2
1.2.1
Zadania praktyczne
Wprowadzenie
Logika zdaniowa znajduje zastosowanie w budowie układów cyfrowych. Poszczególnym funktorom zdaniotwórczym przyporzadkowuje
˛
sie˛ tzw. bramki logiczne.
Nazwa
Funkcja
AND
p∧q
OR
p∨q
NOT
∼p
NAND
p|q
NOR
p↓q
EXOR
p⊕q
Symbol
Symbol w LOGO!
Za pomoca˛ bramek tworzy sie˛ sieci logiczne (układy kombinacyjne), w których stan wyjścia zależy tylko od
bieżacych
˛
stanów wejść. Wejścia i wyjścia moga˛ znajdować sie˛ w jednym z dwóch stanów 0 lub 1. Moga˛ to być
np. dwa rozróżnialne napiecia.
˛
Niektóre bramki tworza˛ zbiory funkcjonalnie pełne, tzn. wykorzystujac
˛ tylko bramki z tego zbioru, można
zrealizować dowolnie złożony układ logiczny. Okazuje sie,
˛ że takich realizacji jest nieskończenie wiele, stad
˛
ważnym zagadnieniem jest upraszczanie (minimalizacja) sieci. Rozróżnia sie˛ metody: algebraiczne (przekształceń formalnych), algorytmiczne (Karnougha, Quine’a-McKluskey’a) i numeryczne.
1.2.2
Przebieg ćwiczenia
1. Uruchomić program LOGO! Soft Comfort.
2. Zapoznać sie˛ z wygladem
˛
okien i menu programu:
• tworzenie nowego schematu: File | New | Function block diagram,
• zapisywanie schematu: File | New | Save as... (ew. Save),
• narzedzia:
˛
Tools:
Wybór
Połaczenia
˛
Stałe, wejścia/wyjścia (Co)
Funkcje podstawowe (GF)
Escape
F5
F6
F7
5
Funkcje specjalne (SF)
Komentarz
Zmiana połaczeń
˛
Symulacja
F8
F9
F11
F3
3. Utworzyć schemat z trójwejściowa˛ bramka˛ AND. Przeanalizować jej działanie.
4. Przeanalizować schemat po przełaczeniu
˛
do jezyka
˛
drabinkowego (ikona Convert to LAD).
5. Przeanalizować działanie pozostałych bramek. Szczególna˛ uwage˛ zwrócić na NAND i NOR.
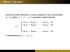
6. Zbadać, jakie funkcje Q1 = f1 (I1 , I2 ), Q2 = f2 (I1 , I2 ) realizuje podany układ?
I1
I2
7. Zbadać symulacyjnie jedno z praw identyczności p ∨ 1 ≡ 1.
8. Zbadać symulacyjnie.
(a)
(b)
(c)
(d)
(e)
pozostałe prawa identyczności
p∨∼p≡1
prawo sprzeczności
∼ (p ∧ q) ≡ ∼ p ∨ ∼ q
drugie prawo de Morgana
9. Zrealizować implikacje.
˛ Sprawdzić symulacyjnie tablice˛ wartości logicznych.
Rozwiazanie:
˛
p ⇒ q ≡ ∼ p ∨ q ≡ ∼ (p ∧ ∼ q).
10. Zrealizować p ⇒ (p ⇒ q).
11. Zrealizować funktory i sprawdzić symulacyjnie tablice wartości logicznych.
(a) p ⇔ q
(b) p ⊕ q
6
Q1
Q2
Ćwiczenie 2
Tautologie. Konsekwencje logiczne.
Rezolucja. Logika pierwszego rzedu
˛
2.1
Zadania teoretyczne
2.1.1
Tautologie
1. Sprawdzić, czy formuła (p ∨ q) ⇒ (∼ p ⇒ q) jest tautologia.
˛
Rozwiazanie:
˛
(a) metoda zero-jedynkowa
p
0
0
1
1
p∨q
0
1
1
1
q
0
1
0
1
∼p
1
1
0
0
∼p⇒q
0
1
1
1
(p ∨ q) ⇒ (∼ p ⇒ q)
1
1
1
1
(b) skrócona metoda zero-jedynkowa
1.
w [(p ∨ q) ⇒ (∼ p ⇒ q)] = 0
2.
w (p ∨ q) = 1
w (∼ p ⇒ q) = 0
3.
w (∼ p) = 1
w (q) = 0
w (p) = 0
4.
(0 ∨ 0) = 1
5.
0 = 1 SPRZECZNOŚĆ
Komentarz: 1. zakładamy fałszywość formuły; 2. ponieważ funktorem głównym jest implikacja, stad
˛ jej
poprzednik musi być prawdziwy, a nastepnik
˛
fałszywy; 3. warunek w (∼ p ⇒ q) = 0 jest fałszywa˛ implikacja,
˛
stad
˛ w (∼ p) = 1, tzn. w (p) = 0 i w (q) = 0; 4. podstawiamy w (p) = 0 i w (q) = 0 do warunku w (p ∨ q) = 1;
5. otrzymujemy sprzeczność, zatem nie udowodniliśmy fałszywości formuły.
(c) metoda przekształcenia do postaci normalnej
(p ∨ q) ⇒ (∼ p ⇒ q) ≡
1.
≡ ∼ (p ∨ q) ∨ [∼ (∼ p) ∨ q] ≡
2.
≡ (∼ p ∧ ∼ q) ∨ (p ∨ q) ≡
≡ ∼p∨p∨q ∧ ∼q∨p∨q ≡
3b.
≡1∧1≡1
Obydwie dysjunkcje elementarne sa˛ tautologiami – pierwsza zawiera pare˛ literałów komplementarnych
{p, ∼ p}, druga zawiera pare˛ {q, ∼ q}.
Odpowied´z: Formuła jest tautologia.
˛
7
2. Sprawdzić trzema metodami, czy formuła jest tautologia.
˛
(a) p ⇒ (p ⇒ q)
(b) (p ∧ q) ⇒ (p ∨ q)
(c) (p ∧ q) ∨ (p ⇒ q)
(d) (p ⇒ q) ⇒ (∼ p ∨ q)
(e) (p ∧ ∼ q) ⇒ ∼ (p ⇒ q)
Odpowied´z: Tautologiami sa˛ formuły: b, d, e.
3. Sprawdzić trzema metodami, czy formuła jest kontrtautologia.
˛
(a) (p ∨ q) ∧ (p ∧ ∼ q)
(b) (p ∧ q) ∧ (p ⇒ ∼ q)
(c) p ∧ ∼ (p ⇒ q)
(d) ∼ [p ⇒ (p ⇒ ∼ q)]
(e) ∼ (p ∨ q) ∧ (∼ p ⇒ q)
Odpowied´z: Kontrtautologiami sa˛ formuły: b, e.
4. Sprawdzić metoda˛ skrócona,
˛ czy formuła jest tautologia.
˛
(a) (p ⇔ q) ⇒ [(p ⇒ q) ∨ q]
(b) [(p ⇒ q) ∧ q] ⇒ (p ⇔ q)
(c) (p ⇒ q) ⇔ (∼ q ⇒ ∼ p)
(d) (∼ p ⇒ q) ⇔ (q ⇒ p)
(e) [(p ∧ ∼ q) ∧ (q ⇔ ∼ r)] ⇒ r
(f) [p ⇒ (q ∧ r)] ⇒ [∼ q ⇒ (p ∨ ∼ r)]
(g) (p ⇒ q) ⇒ {(p ⇒ r) ⇒ [p ⇒ (q ∧ r)]}
Odpowied´z: Tautologiami sa˛ formuły: a, c, e, g.
5. Sprawdzić metoda˛ skrócona,
˛ czy formuła jest kontrtautologia.
˛
(a) (p ⇔ q) ∧ ∼ (p ⇒ q)
(b) ∼ [p ⇒ (∼ q ∧ r)] ∧ (p ⇒ r)
(c) (p ⇒ q) ∧ (∼ q ⇒ ∼ r) ∧ ∼ [(p ∨ r) ⇒ q]
Odpowied´z: Kontrtautologiami sa˛ formuły: a, c.
2.1.2
Konsekwencje logiczne
1. Sprawdzić poprawność wnioskowania: Je´sli funkcja ma pochodna,˛ to jest ciagła,
˛
a je´sli funkcja jest ciagła,
˛
to ma pochodna,˛ a wiec
˛ funkcja ma pochodna,˛ wtedy i tylko wtedy, gdy jest ciagła.
˛
Rozwiazanie:
˛
• schemat wnioskowania można zapisać w trzech postaciach:
p ⇒ q, q ⇒ p
p⇔q
p⇒q
q⇒p
p⇔q
lub
lub
{p ⇒ q, q ⇒ p} |= p ⇔ q
gdzie p – funkcja ma pochodna,˛ q – funkcja jest ciagła,
˛
• korzystamy z definicji konsekwencji logicznej :
p
0
0
1
1
q
0
1
0
1
p⇒q
1
1
0
1
q⇒p
1
0
1
1
Istnieja˛ dwa modele i w każdym z nich wniosek jest prawdziwy.
8
p⇔q
1
0
0
1
• lub stosujemy twierdzenie o dedukcji i badamy np. metoda˛ skrócona,
˛ czy nastepuj
˛
aca
˛ formuła jest tautologia:
˛
[(p ⇒ q) ∧ (q ⇒ p)] ⇒ (p ⇔ q)
• lub korzystamy z metody rezolucji :
— przekształcamy przesłanki i negacje˛ wniosku do postaci klauzulowej:
przesłanki:
p ⇒q ≡ ∼p∨q
q ⇒p≡ ∼q∨p
negacja wniosku:
∼ (p ⇔ q) ≡ (∼ p ∨ ∼ q) ∧ (p ∨ q)
— stosujemy rezolucje˛ dla utworzonego zbioru S = {{∼ p, q} , {∼ q, p} , {∼ p , ∼ q} , {p, q}} :
1.
{∼ p, q}
2.
{∼ q, p}
3.
{∼ p , ∼ q}
4.
{p, q}
5.
{∼ q}
2, 3
6.
{q}
1, 4
7.
5, 6
— sprawdzenie w Prologu:
File | Consult ... (załadować resolve.pl)
?- resolve([[~p,q], [~q,p], [~p,~q], [p,q]]).
[[~p, q], [~q, p], [~p, ~q], [p, q]]
[[~p], [~p, q], [~q, p], [~p, ~q], [p, q]]
[[~q], [~p], [~p, q], [~q, p], [~p, ~q], [p, q]]
[[p], [~q], [~p], [~p, q], [~q, p], [~p, ~q], [p, q]]
[[], [p], [~q], [~p], [~p, q], [~q, p], [~p, ~q], [p, q]]
The empty clause is in the set of clauses so it is unsatisfiable.
Odpowied´z: Wnioskowanie jest poprawne.
2. Sprawdzić trzema metodami (jak w zadaniu 1.) poprawność wnioskowania.
(a) Dzisiaj jest piatek,
˛
a je´sli dzisiaj jest piatek,
˛
to jutro jest sobota, a wiec
˛ jutro jest sobota.
(b) Jeżeli Kazimierz spotkał Tadeusza, to wróci pó´zno. Kazimierz nie spotkał Tadeusza. Zatem Kazimierz
nie wróci pó´zno.
(c) Kazimierz był na meczu lub na zebraniu. Gdyby Kazimierz był na meczu, to nie wstałby dzi´s tak
wcze´snie. Kazimierz wstał wcze´snie. A zatem Kazimierz był na zebraniu.
Odpowied´z: Poprawne jest wnioskowanie: a, c.
3. Sprawdzić trzema metodami, czy U |= B.
(a) U = {p ⇒ q, q ⇒ p} , B = p ∨ q
(b) U = {p ⇒ q, q ⇒ p} , B = p ⊕ q
(c) U = {p ⇒ q, p ∨ q} , B = q
(d) U = {(p ∧ q) ⇒ r} , B = p ⇒ r
Odpowied´z: Zbiór U implikuje logicznie B w przypadku c.
9
2.1.3
Logika pierwszego rzedu
˛
1. Zapisać formuły zdań.
(a) Niektórzy ludzie sa˛ Polakami.
Rozwiazanie:
˛
[P (x) ∧ Q (x)] lub ∼
x
[P (x) ⇒ Q (x)],
P (x) – x jest człowiekiem, Q (x) – x jest Po-
[P (x) ⇒ ∼ Q (x)],
P (x) – x jest rzecza,˛ Q (x) – x jest trwały.
x
lakiem.
(b) Żadna rzecz nie jest trwała.
Rozwiazanie:
˛
∼
[P (x) ∧ Q (x)] lub
x
x
(c) Niektóre ptaki nie sa˛ orłami.
(d) Nie każdy bogacz jest skapcem.
˛
(e) Żadna góra nie jest wieczna.
(f) Niektóre piekne
˛
auta nie sa˛ drogie.
(g) Nie każde piekne
˛
auto jest drogie.
(h) Każdy człowiek jest me˛żczyzna˛ lub kobieta.˛
(i) Nie tylko samochody sa˛ pojazdami.
2. Określić, dla jakich argumentów funkcja zdaniowa jest zdaniem prawdziwym.
(a) x2 x, x ∈ R
(b) x2 x,
x∈N
(c) |x + 1| = 1, x ∈ R
2
x + y 2 = 1, x ∈ R
(d)
y∈R
3. Zaznaczyć na płaszczyźnie zbiór punktów o współrzednych
˛
(x, y) , dla którego funkcja zdaniowa jest
zdaniem prawdziwym.
(a) |x| > y
(b) ∼ (|x| > y)
(c) (x y) ∨ x2 + y 2 1
(d) (x y) ∧ x2 + y 2 < 1
10
2.2
Zadania praktyczne
1. Zrealizować za pomoca˛ bramek NAND, a nastepnie
˛
za pomoca˛ bramek NOR podane formuły.
(a) ∼ p
(b) p ∧ q
(c) p ∨ q
(d) p ⇒ q
(e) p ⇔ q
(f) p ⊕ q
(g) (p ∨ q) ∧ r
(h) (p ∧ q) ∨ (r ∧ s)
2. Dana jest tablica wartości logicznych pewnej formuły. Zrealizować ja˛ tylko za pomoca˛ bramek NAND.
p
0
0
1
1
q
0
1
0
1
A
1
0
0
1
Rozwiazanie:
˛
• na podstawie tablicy piszemy dysjunkcyjna˛ postać normalna:
˛
A = (∼ p ∧ ∼ q) ∨ (p ∧ q)
• wyprowadzamy negacje˛ przed nawias (prawa podwójnego przeczenia i de Morgana):
A = (∼ p ∧ ∼ q) ∨ (p ∧ q) ≡ ∼ [∼ (∼ p ∧ ∼ q) ∧ ∼ (p ∧ q)]
• realizacja:
3. Zrealizować formułe˛ z powyższego zadania tylko za pomoca˛ bramek NOR.
Wskazówka: Na podstawie tablicy przedstawić formułe˛ w koniunkcyjnej postaci normalnej i dalej postepować
˛
podobnie.
11
Ćwiczenie 3
Rachunek zbiorów
3.1
3.1.1
Zadania teoretyczne
Zbiór i zależności miedzy
˛
zbiorami
1. Podać elementy zbiorów:
(a) {a, b, a}
(b) ∅
(c) {{a}}
(d) {∅}
(e) {{a, b} , {a}}
(f) {x ∈ N : x 2}
(g) x ∈ N : x2 7
(h) {x ∈ N : x = 2 ∨ x = 3}
(i) x ∈ N : x2 = 4
(j) {x ∈ N : |3 − x| < 3}
(k) x ∈ R : x2 + 4x + 4 0
2. Zbadać jakie relacje (inkluzji, równości) zachodza˛ miedzy
˛
zbiorami:
(a) A = {a, b, c, d}, B = {a, c, d}
(b) A = {a, b}, B = {a, c, d}
(c) A = ∅, B = {a, b, c}
(d) A = {{a} , a, ∅}, B = {a}
(e) A = {{a, b} , {c, d} , c, d}, B = {{a, b} , c}
(f) A = {{a, b} , {a} , b, ∅}, B = {{a} , b, {∅}}
(g) A = {x ∈ N : x > 2}, B = {y ∈ N : y > 2}
3.1.2
Prawa rachunku zbiorów
1. Udowodnić i sprawdzić na diagramach Venna:
(a) A ∪ (A ∩ B) = A
Rozwiazanie:
˛
• korzystamy z definicji sumy i iloczynu zbiorów:
[x ∈ A ∨ (x ∈ A ∧ x ∈ B)] ⇔ x ∈ A
• oznaczajac
˛ p – x ∈ A, q – x ∈ B zapisujemy formułe:
˛
[p ∨ (p ∧ q)] ⇔ p
• ponieważ otrzymana formuła jest tautologia,
˛ to równość A ∪ (A ∩ B) = A jest prawdziwa.
12
(b) A − B = A ∩ B
(c) (A − B) ∩ B = ∅
(d) (A − B) ∪ B = A ∪ B
(e) A = (A ∩ B) ∪ (A ∩ B)
2. Udowodnić i sprawdzić na diagramach Venna prawa de Morgana dla zbiorów.
3. Udowodnić wzory:
(a) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
(b) (A ∪ B) − C = (A − C) ∪ (B − C)
(c) A − (B ∪ C) = (A − B) − C
(d) [(A − B) = (B − A)] ⇒ (A = B)
(e) (A ⊂ B) ∧ (C ⊂ D) ⇒ (A ∩ C) ⊂ (B ∩ D)
(f) (A ∪ B) − (A ∩ B) = (A − B) ∪ (B − A)
4. Która z podanych inkluzji jest prawdziwa, a która fałszywa:
(a) (A ∩ B) ⊂ (A ∪ B)
(b) (A ∪ A) ⊂ A
(c) (A ∩ A) ⊂ A
(d) (A − B) ⊂ (A ∪ B)
(e) (A − B) ⊂ (A ∩ B)
(f) (A ∩ B) ⊂ A
Odpowied´z: Inkluzje a, b, c, d, f sa˛ prawdziwe; inkluzja e jest fałszywa.
3.1.3
Działania na zbiorach
1. Dla zbioru A = {a, b, c} wyznaczyć 2A .
2. Dane sa˛ zbiory A = {0, 1, 2, 8}, B = {0, 1, 2, 3, 4}. Znaleźć:
(a) A ∪ B
(b) A ∩ B
(c) A − B
(d) B − A
(e) A ⊕ B
3. Niech U = {1, 2, 3, 4, 5} bedzie
˛
przestrzenia.
˛ Znaleźć dopełnienie zbiorów:
(a) A = {2, 3, 5}
(b) B = {1, 2}
4. Dane sa˛ zbiory A = x ∈ R : x2 + 6x + 8 < 0 , B = x ∈ R : x2 + 3x < 0 . Znaleźć:
(a) A ∩ B
(b) A ∪ B
(c) A − B
(d) A
5. Dla zbiorów At = {x ∈ R : −t x t + 1} , gdzie t ∈ N wyznaczyć:
(a)
At
t∈T
(b)
At
t∈T
13
3.2
3.2.1
Zadania praktyczne
Wstep
˛
Twórcami jezyka
˛
Prolog sa˛ Alain Colmerauer i Robert Kowalski. Kowalski podał podstawy teoretyczne, natomiast Colmerauer opracował w 1972 roku jezyk
˛
programowania. Nazwa jest skrótem od Programming in Logic,
co oznacza programowanie w logice. Prolog zyskał popularność w latach osiemdziesiatych,
˛
kiedy Japonia wybrała
go na jezyk
˛
komputerów piatej
˛ generacji, a firma Borland wprowadziła na rynek kompilator Turbo-Prolog.
Pierwotne zastosowania Prologu dotyczyły dowodzenia twierdzeń logicznych i przetwarzania jezyka
˛
naturalnego. Ponieważ Prolog operuje głównie na symbolach, nadaje sie˛ także do rozwiazywania
˛
zagadnień sztucznej
inteligencji takich, jak wnioskowanie logiczne, podejmowanie decyzji czy rozgrywanie gier.
Praca z Prologiem polega na zasadzie zapytań. Zapytanie może być proste, np. Czy 2 jest wieksze
˛
od 1?
?- 2 > 1.
Yes
lub złożone np. Czy 2 jest wieksze
˛
od 1 i czy 3 jest mniejsze od 2?
?- 2 > 1, 5 < 3.
No
Uwaga 3.1 Koniunkcje˛ zapytań realizuje przecinek (,), za´s alternatywe˛ – ´srednik (;). Każde zapytanie musi
kończyć sie˛ kropka.˛
Prolog interpretuje zapytanie i drukuje odpowiedź. Odpowiedź może mieć postać:
1. Yes – odpowiedź twierdzaca,
˛
2. No – odpowiedź negatywna,
3. zmienne i ich wartości – sa˛ drukowane, jeżeli stanowia˛ odpowiedź na zapytanie. Po wydrukowaniu jednej
odpowiedzi, program czeka na decyzje˛ użytkownika. Aby wyświetlić kolejne rozwiazanie,
˛
należy nacisnać
˛
średnik (;). Aby zrezygnować z szukania dalszych odpowiedzi, należy nacisnać
˛ Enter.
Uwaga 3.2 W Prologu zmienne zaczynaja˛ sie˛ wielka˛ litera˛ (np. X, Kto, Delta).
3.2.2
Działania na zbiorach w jezyku
˛
Prolog
W jezyku
˛
Prolog zbiory sa˛ reprezentowane w postaci listy, na przykład:
Zbiór
∅
Lista
[]
{a, b, c}
[a,b,c]
{{a} , {b, c}}
[[a],[b,c]]
Działania na zbiorach realizuja˛ predykaty podane w tabeli:
Nazwa
przynależność
Operacja
x∈A
Predykat
member(X, A)
inkluzja (podzbiór)
A⊂B
subset(A, B)
suma
C =A∪B
union(A, B, C)
iloczyn
C =A∩B
intersection(A, B, C)
różnica
C =A−B
subtract(A, B, C)
Pozostałe działania można zdefiniować z wykorzystaniem wymienionych powyżej (por. wykład).
14
3.2.3
Przebieg ćwiczenia
1. Uruchomić interpreter jezyka
˛
SWI-Prolog.
2. Zapytać: Czy 2 > 1 i 3 < 2?
?- 2 > 1, 3 < 2.
No
3. Zapytać: Czy 2 > 1 lub 3 < 2?
4. Zbadać przynależności:
(a) x ∈ {a, b}
?- member(x, [a,b]).
No
(b) x ∈ {a, x}
(c) ∅ ∈ {∅, a, b}
(d) {a, b} ∈ {a, b, c}
(e) {a, b} ∈ {{a, b} , b, c}
5. Podać wszystkie elementy zbiorów:
(a) {a, b}
?- member(X, [a,b]).
X = a;
X = b;
No
(b) ∅
(c) {∅}
(d) {{a, b} , {b} , b}
(e) {{a} , b, {∅}}
6. Zbadać inkluzje˛ A ⊂ B dla A = {a, {b, c}}, B = {a, {b, c} , d}:
?- A = [a,[b,c]], B = [a,[b,c],d], subset(A,B).
A = [a, [b, c]]
B = [a, [b, c], d]
Yes
7. Zbadać równość zbiorów A = {a, b}, B = {b, a}.
8. Dla zbiorów A = {a, b, c, d}, B = {a, c, d} wyznaczyć:
(a) A ∪ B
?- A = [a,b,c,d], B = [a,c,d], union(A,B,Suma).
Suma = [b, a, c, d]
(b) A ∩ B
(c) A − B
(d) B − A
(e) (A ∪ B) ∩ B
(f) A ⊕ B
9. Wyznaczyć A, A, B, U dla
U = {a, b, c, d} ,
A = {a, c} ,
B = ∅.
10. Dla zbiorów
U = {1, 2, 3, 4, 5} ,
A = {1, 2} ,
zbadać prawa wyłaczonego
˛
środka, sprzeczności i de Morgana.
15
B = {2, 3, 4}
Ćwiczenie 4
Iloczyn kartezjański. Relacje. Funkcje
4.1
Zadania teoretyczne
4.1.1
Iloczyn kartezjański
1. Znaleźć iloczyny kartezjańskie A × B, B × A dla nastepuj
˛ acych
˛
zbiorów:
(a) A = {0, 1}, B = {1, 2}
(b) A = ∅, B = {1, 2, 3}
(c) A = {∅}, B = {1, 2, 3}
2. Znaleźć iloczyn kartezjański A × B × C dla A = {x, y, z}, B = {1, 2}, C = {u}.
Rozwiazanie:
˛
Tworzymy wszystkie trójki (a, b, c), w których a ∈ A, b ∈ B i c ∈ C:
A × B × C = {(x, 1, u) , (x, 2, u) , (y, 1, u) , (y, 2, u) , (z, 1, u) , (z, 2, u)}
3. Niech x, y ∈ R. Podać interpretacje˛ geometryczna˛ iloczynów A × B, B × A dla:
(a) A = {x : 0 < x}, B = {y : 0 < y}
(b) A = {x : 0 < x 1}, B = {y : −1 < y < 1}
(c) A = {x : (0 < x < 1) ∨ (2 < x 3)}, B = {y : (1 < y 2) ∨ (3 < y 4)}
4. Sprawdzić, czy prawdziwe sa˛ równości:
(a) A × (B ∩ C) = (A × B) ∩ (A × C)
(b) A − (B × C) = (A − B) × (A − C)
(c) A ∩ (B × C) = (A ∩ B) × (A ∩ C)
(d) A × (B − C) = (A × B) − (A × C)
4.1.2
Relacje
1. Określić dziedzin˛e, przeciwdziedzin˛e i pole relacji:
(a) {(a, a) , (a, b) , (a, c) , (b, d)}
(b) x jest przełożonym y
(c) x jest wyższy od y
(d) x jest bratem y
2. Określić własności relacji:
(a) x jest dzieckiem y
(b) x jest przeciwnej płci niż y
(c) x ma tyle samo lat co y
(d) x jest starszy od y
(e) x jest starszy o 10 lat od y
16
3. Niech U = {a, b, c, d}. Określić własności relacji:
(a) {(a, a) , (b, b) , (c, c) , (d, d) , (a, b) , (b, a) , (b, c) , (c, b) , (a, c) , (c, a)}
Wskazówka: Przedstawić relacje˛ w postaci tablicy, gdzie w wierszach mamy poprzedniki par, zaś w kolumnach
ich nastepniki.
˛
a b c d
a x x x
b x x x
c x x x
d
x
(b) {(a, a) , (c, c) , (a, b) , (b, c)}
(c) {(b, a) , (a, b) , (c, a) , (a, d) , (c, b) , (b, d) , (d, c)}
4. Określić własności relacji y > x, gdzie x, y ∈ R. Podać ich interpretacje˛ geometryczna.
˛
4.1.3
Funkcje
1. Dana jest funkcja f : R → R, gdzie f (x) = x2 . Zbadać, czy f jest injekcja,
˛ surjekcja˛ i bijekcja.
˛ Jeżeli nie
jest injekcja,
˛ podać x1 i x2 takie, że x1 = x2 i f (x1 ) = f (x2 ). Jeżeli nie jest surjekcja,
˛ podać Wf .
Rozwiazanie:
˛
• funkcja nie jest injekcja,
˛ ponieważ istnieja˛ takie x1 , x2 ∈ R, że (x1 = x2 ) ⇒ [f (x1 ) = f (x2 )], na przykład
x1 = −1, x2 = 1,
• funkcja nie jest surjekcja,
˛ ponieważ dla pewnych y nie istnieje takie x ∈ R, że y = f (x), na przykład dla
y = −4. Mamy tutaj Wf = R+ (zbiór liczb rzeczywistych nieujemnych),
• funkcja nie jest bijekcja,
˛ ponieważ nie jest injekcja˛ (nie jest także surjekcja).
˛
2. Dla danego przekształcenia f : R → R zbadać, czy f jest injekcja,
˛ surjekcja˛ i bijekcja.
˛ Jeżeli nie jest
injekcja,
˛ podać x1 i x2 takie, że x1 =
x2 i f (x1 ) = f (x2 ). Jeżeli nie jest surjekcja,
˛ podać Wf .
(a) f (x) = 2x
(b) f (x) = x3
 2x + 1

x−1
(c) f (x) =

0
dla x = 1
dla x = 1
Wskazówka: Wykorzystać własności funkcji homograficznej.
(d) f (x) = 2x + x
2x
(e) f (x) = 2
x +1
√
x + 1 dla x 0
(f) f (x) =
2x
dla x < 0
(g) f (x) = sin x
3. Dana jest funkcja f : R → R, gdzie f (x) = sin 2x + 1. Wyznaczyć obrazy i przeciwobraz:
(a) f (A), gdzie A = 0, π
π
(b) f (A), gdzie A = 0,
2
−1
(c) f (B), gdzie B = {0}
4. Niech f : R → R, gdzie f (x) = x2 − 3x + 2. Znaleźć obrazy i przeciwobrazy:
(a) f (0, 1)
(b) f (−2, −1)
(c) f −1 ((−∞, −6)
(d) f −1 ({−3, −4})
(e) f ({1, 2})
17
4.2
4.2.1
Zadania praktyczne
Wstep
˛
Iloczyny kartezjańskie i relacje sa˛ zbiorami składajacymi
˛
sie˛ z par uporzadkowanych,
˛
stad
˛ w Prologu sa˛ reprezentowane w postaci listy, na przykład:
Zbiór
{(a, 1) , (a, 2)}
Lista
[(a,1),(a,2)]
{(a, b, 1) , (a, b, 2)}
[(a,b,1),(a,b,2)]
Do generowania zbiorów wykorzystuje sie˛ predykat findall.
Definicja
L = {x : P (x)}
Zapytanie
findall(X, P(x), L)
L = {(x, y) : R (x, y)}
findall((X,Y), R(x,y), L)
Predykat ten zwraca liste˛ L, która zawiera wszystkie wartości zmiennej X lub pary zmiennych (X,Y) spełniajace
˛
funkcje˛ zdaniowa˛ P(x) lub R(x,y).
Uwaga 4.1 Funkcje zdaniowe złożone musza˛ by´c zapisane w nawiasie.
4.2.2
Przebieg ćwiczenia
1. Znaleźć wszystkie elementy zbioru A = {2, 3, 1, 7, 8}, które sa˛ wieksze
˛
od 2:
?- A = [2,3,1,7,8], findall(X,
L = [3, 7, 8]
(member(X,A),
X>2), L).
2. Dany jest zbiór A = {2, 3, 1, 7, 8}. Znaleźć wszystkie elementy x takie, że:
(a) x ∈ A
(b) x 4 (wsk. >=)
(c) 1 < x 7 (wsk. =<)
(d) x2 < 9
3. Znaleźć A × B dla A = {a, b} i B = {1, 2, 3}:
?- A = [a,b], B = [1,2,3], findall((X,Y), (member(X,A), member(Y,B)), L).
L = [(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3)]
4. Znaleźć A × B i B × A dla:
(a) A = {a}, B = {b}
(b) A = {a}, B = {1, 2, 3}
(c) A = {a, b}, B = ∅
(d) A = {a, b}, B = {∅}
5. Znaleźć A2 dla A = {a, b}.
6. Znaleźć A × B × C dla A = {x, y, z}, B = {1, 2}, C = {u}.
7. Dane sa˛ zbiory A = {1, 2}, B = {1, 2, 4}. Niech x ∈ A i y ∈ B. Znaleźć iloczyn kartezjański A × B i
relacje R w nim określone:
(a) A × B = {(x, y)}
(b) R = {(x, y) : x < y}
(c) R = {(x, y) : x > y + 1}
(d) R = {(x, y) : x = y}
(e) R = {(x, y) : x y}
(wsk. Y is X*X)
(f) R = (x, y) : y = x2
18