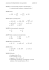ZBIÓR ZADA‹ MATURALNYCH1 Zad 10. Oblicz: Zad 12

ZBIÓR ZADA‹ MATURALNYCH1
Zad 1.
a)
Wyznacz
NW D i NW W
b)
x = 24, y = 66
Zad 2.
podanych liczb:
x = 132, y = 198.
Uzasadnij, »e suma czterech kolejnych liczb naturalnych nie mo»e
by¢ liczb¡ pierwsz¡.
Zad 3.
równa
Dane sa trzy kolejne liczby, których reszta z dzielenia przez
2.
Zad 4.
Jak¡ reszt¦ otrzymamy po podzieleniu sumy tych liczb przez
jest
9?
Uzasadnij, »e suma dwóch liczb dwucyfrowych, ró»ni¡cych sie kolej-
no±ci¡ cyfr, jest liczb¡ podzieln¡ przez
Zad 5.
3
11.
Znajd¹ dwie liczby, których suma jest równa
1530 wiedz¡c, »e pierw-
13
sza liczba stanowi 17 drugiej liczby.
Zad 6.
Drut o dªugo±ci
dªugo±ci jest równy
63
cm poci¦to na cztery cz¦±ci, których stosunek
1 : 3 : 5 : 9.
Oblicz sum¦ dªugo±ci dwóch najkrótszych
kawaªków tego drutu.
Zad 7.
Znajd¹ takie
r,
dla którego pole koªa o promieniu równym
r
jest
liczb¡ wymiern¡.
Zad 8.
a)
b)
5, 3(4)
Zad 9.
a)
Przedstaw w postaci uªamka zwykªego:
√
405
c)
1, (5)
d)
6, 30(9)
5, (034).
Wyª¡cz najwi¦kszy czynnik przed znak pierwiastka:
b)
√
c)
132
Zad 10.
Oblicz:
Zad 11.
Wyznacz warto±¢
√
80
d)
√
1014.
√
√
√
√
a) (3 2 + 18 − 2 8) · 2
√
√
√
√
b) (16 2 − 2 32 + 2 72) : 8
√
√
√
√
c) ( 24 − 4 3 + 2 12) · 6.
a)
√
√
√
2 12 = 3x − 108
Zad 12.
a)
−3
3
a)
· 3 · 3−5
√
√
2 12x = 108 − 2 3x.
b)
(23 )−3 · 24
c)
(( 53 )2 )−4 · (( 53 )−1 )6 .
Przedstaw liczb¦ w postaci pot¦gi:
8−11 · 32−6
1 Na
b)
Oblicz:
6
Zad 13.
x:
b)
8 · 123 : 27−2
c)
6−6 · 274 · 2−6
d)
(257 · 214 ) : 3−21 .
podstawie zbioru zada« dla szkóª ponadgimnazjalnych, wyd. Nowa Era.
1
Zad 14.
a)
16%
Wyznacz liczb¦, której:
jest równe
Zad 15.
a) o
5%
b)
4
2, 5%
jest równe
1 34 .
Wyznacz liczb¦:
mniejsz¡ od
Zad 16.
15%
liczby
W pewnej szkole
30%
b) od której
60
31
jest wi¦ksze o
24%.
uczniów sp¦dziªo wakacje u rodziny, o
25%
mniej osób wyjechaªo wyª¡cznie na obozy sportowe, trzecia cz¦±¢ wszystkich uczniów wypoczywaªa za granic¡, a
34
osoby nigdzie nie wyjechaªy. Ilu
uczniów liczy ta szkoªa?
Zad 17.
Pomara«cze i cytryny kosztuj¡ tyle samo. O ile procent wi¦cej
zapªacimy za
2
pomara«cze o
Zad 18.
kg cytryn i
4
kg pomara«czy je»eli cytryny zdro»ej¡ o
a
14%?
Lodówka kosztowaªa
ka»dym razem o
Zad 19.
8%,
30%.
1300
zª. Jej cen¦ obni»ano dwukrotnie, za
Ile kosztuje lodówka po obni»kach?
Cena brutto pewnego towaru jest równa
zª i zawiera
3075
23%
podatku VAT. Oblicz cen¦ brutto tego towaru po obni»ce podatku VAT do
8%.
Zad 20.
liczba
Liczba
x stanowi 25% liczby y .
Oblicz jaki procent liczby
x stanowi
y.
Zad 21.
Liczba
nowi liczba
Zad 22.
x
stanowi
125%
liczby
y.
Oblicz jaki procent liczby
x
sta-
y.
Zmieszano dwa roztwory soli o st¦»eniach
i
17%
2%.
Otrzymano
roztwór pi¦cioprocentowy. Którego roztworu byªo wi¦cej i o ile?
Zad 23.
Cen¦ telewizora najpierw podniesiono, a potem obni»ono o
Cena ko«cowa jest o
1%
ni»sza od pocz¡tkowej. Oblicz
p%.
p.
Zad 24. Ile elementów ma zbiór: X = {n ∈ N: n|36}?
Zad 25. Jaka jest najmniejsza liczba w zbiorze: Z = {k ∈ C: k2 ≤ 20}?
Zad 26. Na sprawdzianie z matematyki byªy dwa zadania. Spo±ród 24
uczniów
18
rozwi¡zaªo pierwsze zadanie,
16
-
drugie, a
2
uczniów nie roz-
wi¡zaªo »adnego zadania. Ilu uczniów rozwi¡zaªo oba zadania?
Zad 27.
a)
Ile liczb caªkowitych nale»y do przedziaªu:
√ √
⟨− 5, 5⟩
b)
⟨− 73 , 43 ⟩
c)
2
(−π, π).
Zad 28.
Oblicz sum¦:
do przedziaªu
Zad 29.
⟨−3, 7),
Znajd¹
k,
n + m,
a
n
gdzie
m
to ilo±¢ liczb caªkowitych nale»¡cych
to ilo±¢ liczb caªkowitych z przedziaªu
⟨−7, 3).
dla którego speªniony jest warunek:
⟨−k − 3, k 2 − 8⟩ ⊂ (0, 10).
Zad 30.
Zapisz przedziaª, do którego nale»¡ liczby odlegªe od liczby
mniej ni»
2.
Zad 31.
Rozwi¡» nierówno±¢:
a)
√
√
3x + 3 ≥ x + 3 3
Zad
32.
√
a)
b)
Uzasadnij, »e liczba
Zad 35.
(9 +
332 − 1
Oblicz:
√
√
√
17 + 12 2 − 9 + 4 2
o
√
√
√
2x + 3 ≥ 6 + 3x.
Oblicz:
√ √
√
2 7+3· 2 7−3
Zad 33.
Zad
34.
√
a)
b)
1
√ 2
√
11) − (9 − 11)2 .
jest podzielna przez
√
b)
16.
√
√
√
38 − 12 2 + 3 − 2 2.
Zapisz odpowiednie nierówno±ci:
a)
b)
Zad 36.
liczby
2
Zapisz w postaci nierówno±c zbiór tych liczb, których odlegªo±¢ od
jest nie wi¦ksza ni»
6.
3
Zad 37.
a)
Upro±¢ wyra»enie:
|x − 1| + |2 − x|, je»eli x ∈ ⟨1, 2⟩
Zad 38.
Zad 39.
|2x + 4| + |3 − 2x|, je»eli x ∈ ⟨2, ∞).
Znajd¹ iloczyn liczb speªniaj¡cych równanie:
Udowodnij, »e je±li
x2 +y 2 +2
a)
x+y
Zad 40.
b)
≥2
1
b) x
Funkcja
f
+
x > 0 i y > 0,
1
y
≥
| − 2x − 4| = 10.
to zachodzi podana nierówno±¢:
4
.
x+y
przyporz¡dkowuje ka»dej liczbie naturalnej z przedziaªu
⟨2, 18⟩ liczb¦ jej dzielników naturalnych.
Dla ilu argumentów funkcja
f
przyj-
muje warto±¢ 2?
Zad 41.
Funkcja
f
przyporz¡dkowuje ka»dej dodatniej liczbie trzycyfowej
iloczyn jej cyfr. Ile miejsc zerowych ma ta funkcja?
Zad 42.
prostej
a)
y = −6x + 5
P (1, −4)
Zad 43.
prostej
a)
b)
i przechodz¡ca przez punkt:
P ( 15 , − 15 )
c)
P (1 −
√
√
2
,3
2
2 + 2).
Wyznacz wzór funkcji, której wykresem jest prosta prostopadªa do
y = 2x + 3
b)
P (4, 1)
Zad 44.
a)
Wyznacz wzór funkcji, której wykresem jest prosta równolegªa do
i przechodz¡ca przez punkt:
P (−2, −3)
P ( √12 , 3).
c)
Wyznacz wzór funkcji liniowej
je±li:
f (0) = −2, f (12) = 4.
f (0) = 1, f (11) = 45
Zad 45.
f,
Wyznacz warto±ci parametru
m,
dla których proste l1 i l2 s¡ rów-
nolegªe:
a) l1
: y = −2x − 4, l2 : y = (m − 4)x + 6
b) l1
:y=
Zad 46.
m+3
x
2
Wyznacz warto±¢ parametru
jest liczba
2:
a)
3
x
4
f (x) =
Zad 47.
− 1, l2 : y = (2m − 1)x + 3.
+m
b)
m,
je»eli miejscem zerowym funkcji
f (x) = (2 − 3m)x + 2m.
Zapisz równania ogólne i kierunkowe prostych zawieraj¡cych prze-
k¡tne prostok¡ta ograniczonego prostymi:
Zad 48.
x = −2, x = 3, y = −1, y = 4.
2x + 6y − 5 = 0
i
2mx + 5y − 3 = 0
i
Wyznacz równanie prostej równolegªej do prostej
przechodz¡cej przez punkt
Zad 49.
f
P (−1, 4).
Dla jakich warto±ci parametru
10x + my + 1 = 0
m
proste:
s¡ prostopadªe, a dla jakich - równolegªe?
4
Zad 50.
a)
Dla jakich warto±ci parametru
f (x) = (3 − 2m)x + 1
Zad 51.
b)
funkcja
f
jest malej¡ca:
f (x) = 2(m + 2)x − 3.
Podaj dziedzine i miejsca zerowe funkcji:
a)
f (x) =
e)
f (x) =
Zad 52.
x+2
x2 −9
x−3
x2 −9
b)
3x−1
x2 −2
1
= √x−3
.
c)
f (x) =
f)
f (x)
f (x) =
x
x2 +4
d)
f (x) =
√
6−x
Naszkicuj wykres funkcji:


4



f (x) =
Zad 53.
m
x2
dla
x < −2
dla
x ∈ ⟨−2, 2⟩



 6 − x dla x > 2.
Odczytaj z wykresu funkcji
f : ⟨−4, 4⟩ → R jej zbiór warto±ci,
dzie-
dzin¦, miejsca zerowe, warto±¢ najmniejsz¡ i najwi¦ksz¡, oraz argumenty, dla
których s¡ przyjmowane:
Zad 54.
Punkt
funkcji
Wyznacz brakuj¡ce wspóªczynniki i podaj wzór tej funkcji:
a)
f.
W (2, −5)
f (x) = 3x2 + bx + c
Zad 55.
jest wierzchoªkiem paraboli b¦d¡cej wykresem
b)
Dana jest funkcja
f (x) = ax2 + 12x + c.
f (x) = x2 + bx + 2.
je±li:
a) do wykresu funkcji
b) wykres funkcji
f
f
nale»y punkt
A(−2, 0)
jest styczny do osi
5
OX .
Wyznacz wspóªczynnik
b,
Zad 56.
Rozwi¡» równanie:
7x − 12x + 5
b) −4x2 + 3x −
√
d) 2x2 − 3 3x − 9 = 0.
a)
2
Zad 57.
Wyznacz wspóªczynniki
b i c,
9
16
c)
=0
wiedz¡c, »e:
x0 = −4
a) funkcja
f
ma dokªadnie jedno miejsce zerowe
b) funkcja
f
przyjmuje warto±ci dodatnie tylko dla
c) wykres funkcji
Zad 58.
f
przecina o±
OX
−3x2 + 8x − 11 = 0
w punktach
x ∈ (− 23 , 0)
√
√
(− 2, 0) i (1 + 2, 0).
Miejscami zerowymi funkcji kwadratowej
f
s¡ liczby
−2 i 1.
Wy-
znacz wzór tej funkcji, je»eli:
a) dla argumentu
3
funkcja
przyjmuje warto±¢
b) wykres funkcji
f
przecina o±
f
c) warto±¢ najwi¦ksza funkcji
Zad 59.
w punkcie
jest równa
(0, −6)
9.
Rozwi¡» nierówno±ci:
a)
x2 − 2x − 3 ≥ 0
d)
−6x2 + x − 1 > 0.
Zad 60.
f
OY
10
b)
2x2 + 4x − 1 < 0
c)
5x2 − 3x + 2 ≥ 0
Wyznacz wszystkie liczby caªkowite speªniaj¡ce nierówno±¢:
2x2 + 2x − 15 < 0.
Zad 61.* Dla jakich warto±ci par. m równanie ma dwa ró»ne pierwiastki:
a)
x2 + 2mx + 1 = 0
Zad 62.*
b)
(m2 − 4)x2 − 2mx − 2 = 0.
Dla jakich warto±ci parametru
m
równanie ma dwa pierwiastki
o ró»nych znakach:
a)
x2 + (4 − m)x − 4m + m2 = 0
b)
x2 − (2m + 1)x + m2 + m − 6 = 0.
Zad 63.* Wyznacz warto±ci parametru m, dla których dwa ró»ne pierwiastki
równania:
Zad 64.
s¡ liczbami mniejszymi od
2.
Suma kwadratów trzech kolejnych nieparzystych liczb naturalnych
jest równa
Zad 65.
x2 − (m + 1)x + m = 0
251.
Znajd¹ te liczby.
Wyznacz warto±¢ najwi¦ksz¡ i warto±¢ najmniejsz¡ funkcji
w podanym przedziale:
a)
f (x) = −x2 + 4x, ⟨0, 5⟩
b)
f (x) = 2x2 + 5x − 4, ⟨−2, −1⟩.
6
f
Zad 66.
Na okr¦gu obrano
n
ró»nych punktów. Ka»dy z nich poª¡czono
odcinkami ze wszystkimi pozostaªymi punktami. Otzrymano
odcinków.
21
Ile byªo punktów?
Zad 67.
Podaj miary k¡tów w trójk¡cie, wiedz¡c »e ich stosunek wynosi
2 : 3 : 7.
Zad 68.
Dany jest trójk¡t
wierzchoªek
nej k¡ta
B
Zad 69.
Prosta
l
przecina prost¡
ACB , punkt M
ABC
AC
ma miar¦
150◦ .
Przez
równolegª¡ do dwusiecz-
l
w punkcie
MN
(rys.). Póªprosta
jest ±rodkiem odcinka
CB .Wiedz¡c, »e miara k¡ta ABC
Zad 70.
BCA
D.
Oblicz miary
BCD.
Dany jest trójk¡t
»e odcinek
w którym k¡t
tego trójk¡ta poprowadzono prost¡
BCA.
k¡tów trójk¡ta
ABC ,
to
CL
AL, a punkt N
45
◦
i miara k¡ta
jest prostopadªy do odcinka
jest dwusieczn¡ k¡ta
jest ±rodkiem odcinka
ACB
to
60◦ , uzasadnij,
CB .
Przeciwprostok¡tna trójk¡ta prostok¡tnego ma dªugo±¢
ko±¢ opuszczona na przeciwprostok¡tn¡ dzieli j¡ w stosunku
10.
2 : 3.
Wyso-
Oblicz t¦
wysoko±¢ oraz dªugo±ci przyprostok¡tnych.
Zad 71.
Chªopiec stoj¡cy
3
m od latarni rzuca cie« dªugo±ci
wysoko±¢ latarni, je±li chªopiec ma
170
7
cm wzrostu.
1
m. Oblicz
Zad 72.
Na rysunku przedstawiono trójk¡t prostok¡tny o przyprostok¡tnych
dªugo±ci
a, b
a)
h=
i przeciwprostok¡tnej dªugo±ci
ab
x+y
Zad 73.
b)
√
h = xy .
a)
7.
2
3
b)
cos α = 0, 4
Wyka», »e dla k¡ta ostrego
c)
α
tan α =
b)
(sin α + cos α)(sin α − cos α) = 1 − 2 cos2 α.
Zad 76.
Oblicz pole trójk¡ta
i
BAC
k¡ta
Zad 77.
wiedz¡c, »e:
√
√
|AB| = 2 3, |AC| = 2 5
1
jest równy 4 .
Oblicz pole i obwód trapezu równoramiennego wiedz¡c, »e jego
ramie ma dªugo±¢
cos α =
ABC
α:
3
.
5
podana równo±¢ jest to»samo±ci¡:
(1 + cos α)(1 − cos α) = sin2 α
Zad 78.
a jedna z przy-
Oblicz dªugo±ci pozostaªych boków trójk¡ta.
a)
cos
√
8 + 5 2,
Oblicz warto±ci pozostaªych funkcji trygonometr. k¡ta ostrego
sin α =
Zad 75.
Wyka», »e:
Obwód trójk¡ta prostok¡tnego jest równy
prostok¡tnych ma dªugo±¢
Zad 74.
x + y.
7,
krótsza podstawa
5,
a wysoko±¢ jest równa
Oblicz wysoko±¢ i pole rombu o boku
5
i k¡cie ostrym
√
3 5.
α
takim, »e
1
.
5
Zad 79.
Przek¡tne kwadratu przecinaj¡ si¦ w punkcie
wierzchoªków ma wspóªrz¦dne
(1, −2).
8
(2, 1),
a jeden z jego
Oblicz pole i obwód kwadratu.
Zad 80.
AB ,
je±li punkt
Zad 81.
a)
S(5, 6)
A
jest ±rodkiem odcinka
le»y na osi
OY ,
a rz¦dna punktu
Oblicz dªugo±¢ odcinka
B
b)
√
S(−5, −1), r = 2 5.
Oblicz wspóªczynnik
a
wielomianu
w(x) = x2 −ax+2, w(2) = 4
Zad 83.
AB .
Podaj równanie okr¦gu o ±rodku w punkcie
S(1, 3), r = 2
Zad 82.
a)
Punkt
b)
Dane s¡ wielomiany:
h(x) = 7x2 − 2x − 3x3 .
w,
jest równa
S
7.
i promieniu
r:
je±li:
w(x) = ax3 −5x2 +x, w(1)−w(−1) =
3
.
2
f (x) = 6x3 − 5x2 − 4, g(x) = −2x2 − x + 3,
Wyznacz wielomian
w(x) = f (x) + g(x) − 21 h(x)
i
podaj jego stopie«.
Zad 84.
a)
Nie wykonuj¡c mno»enia podaj stopie« wielomianu:
w(x) = (3 − x2 )(1 − x + 2x2 )
Zad 85.
w(x) = (5x3 − 1)(3 − x − x3 ).
Rozªó» wielomian na czynniki:
a)
w(x) = x6 + 2x4 + x2
c)
w(x) = 6x3 − 9x2 + 4x − 6
Zad 86.
b)
b)
w(x) = 5x7 − 2x5 + 0, 2x3
d)
w(x) = x5 + x4 − x − 1.
Rozwi¡» równania:
a)
27x3 − 9x2 − 3x + 1 = 0
c)
2x3 − 7x2 + 7x − 2 = 0
b)
4x6 − 9x4 − 16x2 + 36 = 0
d)
4x3 − 3x2 + 4x − 3 = 0.
b)
x4 + 2x3 − 4x2 − 2x + 3 = 0.
Zad 87.* Rozwi¡» równania:
a)
2x3 − 7x2 − 2x + 1 = 0
Zad 88.
a)
Rozwi¡» równania:
5
8x = 2x3
Zad 89.
b)
x5 = 9x.
Wyznacz równanie hiperboli wiedz¡c, »e powstaªa ona w wyniku
przesuni¦cia hiperboli
punkcie
a)
h
o pewien wektor, a jej asymptoty przecinaja sie w
P:
h : y = x9 , P (−1, 3)
Zad 90.
b)
h: y=
5
, P (−4, −2).
4x
Beata poprosiªa kole»anki o pomoc w wypisaniu
72
zaprosze«.
Poniewaz dwie z nich nie przyszªy, ka»da z pozostaªych dziewcz¡t musiaªa
wypisa¢ o sze±¢ zaprosze« wi¦cej, ni» zaplanowaªa Beata. Ile osób wypisywaªo zaproszenia, je»eli wiadomo, »e ka»da z nich wypisaªa ich tyle samo?
9
Zad 91.
Dwie kopiarki o ró»nej wydajno±ci, pracuj¡c jednocze±nie, sko-
piowaªy pewn¡ liczb¦ ulotek. Skopiowanie tylu ulotek zaj¦ªoby pierwszej z
nich trzy razy wi¦cej czasu, a drugiej o cztery minuty wi¦cej.
Jak dªugo
trwaªo kopiowanie ulotek?
Zad 92.
Z miest A i B oddalonych od siebie o
210
km wyjechaªy jedno-
cze±nie naprzeciw siebie dwa samochody. Poruszaªy sie ze staª¡ pr¦dko±ci¡ i
min¦ªy sie w odlegªo±ci
wiedz¡c, »e jeden jechaª o
Zad 93.
km od miasta A. Oblicz pr¦dko±¢ ka»dego z nich
90
15
Tras¦ o dªugo±ci
km/h szybciej.
144
km samochód przejechaª w czasie o godzin¦
krótszym ni» motocykl. Oblicz ±redni¡ pr¦dko±¢ ka»dego z pojazdów na tym
odcinku, je±li ±rednia pr¦dko±¢ samochodu byªa o
24
km/h wi¦ksza ni» ±red-
nia pr¦dko±¢ motocykla.
Zad 94.
Pr¦dko±¢ wody w nurcie rzeki wynosi
kajakarz pokonaª tras¦ o dªugo±ci
16
2
km/h. Pªyn¡c z pr¡dem,
km w czasie o
2
godziny krótszym, ni»
zaj¦ªa mu druga powrotna w gór¦ rzeki. Ile czasu ª¡cznie pªyn¡ª kajakarz?
Zad 95.
Samochód dostawczy wyjechaª z miasta A do miasta B. Dotarª do
celu i po
15
chaª
km, a caªa podró» zaj¦ªa mu
160
minutach postoju wyruszyª w drog¦ powrotn¡. Š¡cznie przeje-
2, 5
godziny. Oblicz ±redni¡ pr¦dko±¢
samochodu na trasie z miasta A do miasta B wiedz¡c, »e byªa ona o
16 km/h
mniejsza ni» ±rednia pr¦dko±¢, z jak¡ poruszaª sie w drodze powrotnej.
Zad 96.
Ksi¡»ka ma
216
stron.
Konrad czytaª codziennie po tyle samo
stron i sko«czyª ksi¡»k¦ o jeden dzie« wcze±niej ni» Sta±. Ile dni Sta± czytaª
ksi¡»k¦, je»eli ka»dego dnia czytaª o
Zad 97.
a)
70
strony mniej ni» Konrad.
Oblicz pi¦¢ pocz¡tkowych wyrazów ci¡gu
an = n +
Zad 98.
3
(−1)n
n
b)
n
c)
an = (−2)
an =
(an ):
1+(−1)n
2n
d)
an =
3+(−1)n
2
+
1
.
n
Za trzy ksi¡»ki, których ceny tworz¡ ci¡g geometryczny, zapªacono
zª. Najdro»sza z nich kosztowaªa o
10
zª wi¦cej ni» dwie pozostaªe razem.
Ile kosztowaªa ka»da z ksi¡»ek?
Zad 99.
Suma trzech liczb tworz¡cych ci¡g arytmetyczny wynosi
pierwsz¡ i drug¡ liczb¦ zwi¦kszymy o
1,
geometryczny. Wyznacz te liczby.
10
a trzeci¡ - o
4,
15.
Je±li
to otrzymamy ci¡g
Zad 100.
Oblicz pole wycinka koªa o promieniu
4
wyznaczonego przez k¡t
±rodkowy o mierze:
a)
30◦
b)
45◦
c)
252◦ .
Zad 101.
Wyznacz miary k¡tów
Zad 102.
Oblicz promie« okr¦gu opisanego na trójk¡cie prostok¡tnym wie-
dz¡c, »e pole trójk¡ta wynosi
k¡tn¡ jest równa
Zad 103.
8,
α, β i γ :
a wysoko±¢ opuszczona na przeciwprosto-
2.
Oblicz promie« okr¦gu wpisanego w trójk¡t prostok¡tny wiedz¡c,
»e przyprostok¡tne tego trójk¡ta maj¡ dªugo±¢
Zad 104.
Oblicz wysoko±¢ i pole rombu, o którym wiadomo, »e miara jego
k¡ta ostrego wynosi
Zad 105.
a)
60◦ ,
a bok ma dªugo±¢
16
cm.
Zapisz liczb¦ w postaci pot¦gi o podstawie
√
2 · 20,25
Zad 106.
7 i 1.
b)
4 · (0, 5)
3
5
c)
Naszkicuj wykres funkcji
2
9
64 : 0, 25
f (x) = 4x .
2:
5
6.
Odczytaj z wykresu argu-
menty, dla których funkcja przyjmuje warto±ci mniejsze od 1.
Zad 107.
Dana jest funkcja
zerowym funkcji jest liczba
Zad 108.
a)
f (x) = ( 23 )x + a.
Oblicz
a,
je»eli miejscem
−2.
Oblicz:
log4 2 − log4 32 − 6 log4 1
b)
log3 12 + 2 log3 6 − 4 log3 2.
11
Zad 109.
Zad 110.
go±¢
8
√
Oblicz:
ab2
, je»eli
c
log3 a = 5, log2
1
8
= b, logc 9 = 4.
Przek¡tna graniastosªupa prawidªowego czworok¡tnego ma dªu-
i tworzy z kraw¦dzi¡ podstawy k¡t
60◦ .
Oblicz wysoko±¢ tego grania-
stosªupa.
Zad 111.
Przekrojem osiowym sto»ka jest trójk¡t prostok¡tny o polu 25 cm2 .
Oblicz ±rednic¦ podstawy tego sto»ka.
Zad 112.
4π 2 .
Powierzchnia boczna walca po rozwini¦ciu jest kwadratem o polu
Oblicz obj¦to±¢ tego walca.
Zad 113.
Losujemy jedn¡ liczb¦ spo±ród liczb naturalnych dwucyfrowych.
Oblicz prawdopodobie«stwo, »e ta liczba jest podzielna przez
Zad 114.
W urnie jest
20
kul ponumerowanych od
1
do
11.
20.
Wyjmujemy
losowo jedn¡ kul¦. Oblicz prawdopodobie«stwo, »e b¦dzie to kula o numerze
b¦d¡cym liczba pierwsz¡.
Zad 115.
nosi
3.
Ucze« ma osiem ocen z biologii, a ich ±rednia arytmetyczna wy-
O ile wzro±nie ta ±rednia, je»eli otrzyma jeszcze dwie oceny:
Zad 116.
W klasie A licz¡cej
27
osób i klasie B licz¡cej
18
4 i 6.
osób przepro-
wadzono sprawdzan ze statystyki. ‘rednia ocen ze sprawdzianu w klasie A
wyniosªa
4,
a w klasie B -
3, 5.
Oblicz ±redni¡ ocen ze sprawdzianu w obu
tych klasach.
Zad 117.
Wypisz liczby pierwsze mniejsze ni»
50.
Oblicz ±redni¡ i wyznacz
median¦ tych liczb.
Zad 118.
ostrym i
Oblicz warto±¢ wyra»enia:
tan α = 2.
12
cos α+sin α
wiedz¡c, »e
cos α
α
jest k¡tem