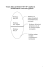Bez tytułu slajdu

Suma dwóch grafów
G1 = (V(G1), E(G1))
G2 = (V(G2), E(G2))
V(G1) i V(G2) – rozłączne
Suma G1 ∪ G2 – graf ze zbiorem wierzchołków V(G1) ∪ V(G2) i
rodziną krawędzi E(G1) ∪ E(G2)
G1
G1 ∪ G2
G2
Zespolenie dwóch grafów
G1 = (V(G1), E(G1))
G2 = (V(G2), E(G2))
V(G1) i V(G2) – rozłączne
Zespolenie G1 + G2 – bierzemy sumę G1 ∪ G2 i prowadzimy
krawędzie z każdego wierzchołka V(G1) do każdego wierzchołka
V(G2).
G1
G2
Matematyka Dyskretna, Podstawy Logiki i Teorii Mnogości
Barbara Głut
G1 + G2
1
Odrzucanie
Jeżeli e jest krawędzią grafu G, to G – e jest grafem otrzymanym z G po
odrzuceniu krawędzi e.
V
W
U
V
W
Y
X
U
Y
X
Jeżeli v jest wierzchołkiem grafu G, to G – v jest grafem otrzymanym z G
po usunięciu z G wierzchołka v wraz z przyległymi do niego
W
krawędziami.
U
Y
X
Ściągnięcie
G \ e – graf otrzymany w wyniku ściągnięcia krawędzi e i utożsamienia
jej końców v oraz w i to w taki sposób, że otrzymany wierzchołek jest
incydentny z tymi krawędziami, które przedtem były incydentne z v i
w (z wyjątkiem krawędzi e).
V
W
U
U
Y
Z
X
Y
Matematyka Dyskretna, Podstawy Logiki i Teorii Mnogości
Barbara Głut
2
Trasa (marszruta) w grafie G – skończony ciąg krawędzi
v0 → v1 → v2 → ... → vm
w którym każde dwie kolejne krawędzie są albo sąsiednie, albo
identyczne.
długość trasy – liczba krawędzi w trasie.
Trasa wyznacza pewien ciąg wierzchołków, gdzie
v0 – początek, vm – koniec
Ścieżka (łańcuch) – trasa, w której wszystkie krawędzie są różne.
Droga – ścieżka, w której ponadto wszystkie wierzchołki są różne.
Ścieżka lub droga są zamknięte,
zamknięte gdy v0 = vm.
Cykl – Droga zamknięta zawierającą przynajmniej jedną krawędź
Obwód grafu – długość najkrótszego cyklu w tym grafie.
Przykład:
V
W
Y
X
U
Trasa:
V → U → Y → V → W → Y → U o długości 6.
Ścieżka: V → U → Y → V → W → Y
Droga: V → U → Y → W → X
Cykl:
V→U→Y→X→W→V
Obwód: 3
Matematyka Dyskretna, Podstawy Logiki i Teorii Mnogości
Barbara Głut
3
Spójność grafu
Graf jest spójny, gdy nie może być przedstawiony w postaci sumy
dwóch grafów.
Graf jest spójny, gdy dowolna para wierzchołków grafu jest
połączona drogą.
Graf niespójny - w przeciwnym przypadku.
Dowolny niespójny graf może być przedstawiony jako suma skończonej
liczby grafów spójnych, zwanych składowymi spójnymi grafu.
Twierdzenie:
Każdy graf prosty, który ma n wierzchołków i więcej niż (n–1)(n–2)/2
krawędzi, jest spójny.
spójny
8 wierzchołków
9 krawędzi
niespójny
8 wierzchołków
8 krawędzi
Pytanie:
jak bardzo graf spójny jest spójny?
To znaczy: ile krawędzi lub wierzchołków należy usunąć, aby graf stał
się niespójny?
Matematyka Dyskretna, Podstawy Logiki i Teorii Mnogości
Barbara Głut
4
Zbiór rozspajający grafu spójnego G
– zbiór krawędzi, których usunięcie spowoduje, że graf G przestanie być
spójny.
V
W
V
W
Y
X
U
U
Y
X
Zbiór rozspajający: {e1, e2, e5} lub {e3, e6, e7, e8}
Rozcięcie – zbiór rozspajający, którego żaden podzbiór właściwy nie
jest już zbiorem rozspajającym.
Np. {e3, e6, e7, e8}
Most
– jeżeli rozcięcie składa się z jednej krawędzi, to krawędź tę
nazywamy mostem.
Spójność krawędziowa λ(G) – w grafie spójnym jest to liczba
krawędzi należących do najmniej licznego rozcięcia grafu.
Tzn. jest to najmniejsza liczba krawędzi, które należy usunąć, aby graf
przestał być spójny.
Graf jest k–spójny krawędziowo, jeśli λ (G) ≥ k.
1-spójny i 2-spójny krawędziowo,
ale nie 3-spójny
Matematyka Dyskretna, Podstawy Logiki i Teorii Mnogości
Barbara Głut
5
Zbiór rozdzielający grafu spójnego G
– zbiór wierzchołków, których usunięcie spowoduje, że graf przestanie
być spójny.
V
W
W
U
U
Y
X
X
Zbiór rozdzielający: {V, Y}
Spójność wierzchołkowa κ(G)
– Jeżeli graf G jest spójny i nie jest pełny, to spójnością
wierzchołkową grafu G nazywamy liczbę elementów najmniejszego
zbioru rozdzielającego.
Graf jest k–spójny wierzchołkowo, jeśli κ (G) ≥ k.
Wierzchołek rozcinający
– Jeżeli zbiór rozdzielający składa się tylko z jednego wierzchołka, to
ten wierzchołek nazywamy wierzchołkiem rozcinającym.
Matematyka Dyskretna, Podstawy Logiki i Teorii Mnogości
Barbara Głut
6
Grafy eulerowskie
Graf spójny G nazywamy grafem eulerowskim,
eulerowskim jeżeli istnieje
ścieżka zamknięta zawierająca każdą krawędź G.
Taką ścieżkę nazywamy cyklem Eulera.
Eulera
Uwaga: nazwa „cykl”, choć od cyklu żąda się by był drogą.
Niekonsekwencja ze względu na tradycyjną nazwę.
Jak narysować ten graf bez odrywania
ołówka i bez rysowania tej samej linii
wielokrotnie?
Grafy półeulerowskie
Graf, który nie jest grafem eulerowskim, nazywamy
półeulerowskim,
półeulerowskim jeżeli istnieje ścieżka zawierająca każdą
krawędź grafu G.
Graf półeulerowski
Graf, który nie jest eulerowski
ani półeulerowski
Matematyka Dyskretna, Podstawy Logiki i Teorii Mnogości
Barbara Głut
7
Problem mostów królewieckich
Czy można przejść dokładnie jeden raz przez każdy z siedmiu
mostów i powrócić do punktu wyjścia?
Rozwiązane przez Eulera
Pytanie:
Czy możliwe jest znalezienie warunku koniecznego
i wystarczającego na to, by graf był eulerowski?
Twierdzenie (Euler,
Euler, 1776): Graf spójny G jest grafem eulerowskim
wtedy i tylko wtedy, gdy stopień każdego wierzchołka grafu G jest
liczbą parzystą.
Twierdzenie:
Twierdzenie: Graf spójny G jest grafem półeulerowskim wtedy i tylko
wtedy, gdy ma dokładnie dwa wierzchołki nieparzystych stopni.
W grafie półeulerowskim każda ścieżka Eulera musi zaczynać się w
jednym wierzchołku nieparzystego stopnia i kończyć w drugim
takim wierzchołku.
Matematyka Dyskretna, Podstawy Logiki i Teorii Mnogości
Barbara Głut
8
Uwaga: żaden graf nie może mieć dokładnie jednego
wierzchołka nieparzystego stopnia.
To wynika z lematu o uściskach dłoni:
dłoni jeśli pewne osoby witają się
podając sobie dłonie, to łączna liczba uściśniętych dłoni jest parzysta.
W każdym grafie suma stopni wszystkich wierzchołków
jest liczbą parzystą.
W każdym grafie liczba wierzchołków o nieparzystych
stopniach jest parzysta.
Algorytm Fleury’ego
służy do konstrukcji cyklu Eulera w grafie eulerowskim
Zacznij cykl w dowolnym wierzchołku u i przechodź krawędzie w
dowolnej kolejności, dbając jedynie o zachowanie następujących
reguł:
(1) usuwaj z grafu przechodzone krawędzie i wierzchołki izolowane
powstające w wyniku usuwania krawędzi;
(2) w każdym momencie przechodź przez most tylko wtedy, gdy nie
masz innej możliwości.
Matematyka Dyskretna, Podstawy Logiki i Teorii Mnogości
Barbara Głut
9
Grafy hamiltonowskie
Czy istnieje zamknięta ścieżka przechodząca dokładnie jeden
raz przez każdy wierzchołek grafu spójnego G?
Taka ścieżka musi być cyklem → cykl Hamiltona
Graf, w którym istnieje cykl Hamiltona nazywamy
grafem hamiltonowskim.
Graf półhamiltonowski
graf, który nie jest hamiltonowski i w którym istnieje droga
przechodząca dokładnie jeden raz przez każdy wierzchołek
graf półhamiltonowski
graf niehamiltonowski
Matematyka Dyskretna, Podstawy Logiki i Teorii Mnogości
Barbara Głut
10
Dla grafów hamiltonowskich nie ma udowodnionych warunków
koniecznych i wystarczających takich, jak w przypadku grafów
eulerowskich.
Twierdzenie (Dirac,
Dirac, 1952): Jeżeli w grafie prostym G o n
wierzchołkach (n ≥ 3), stopień każdego wierzchołka jest
większy bądź równy n/2, to graf G jest hamiltonowski.
Twierdzenie (Ore,
Ore, 1960): Jeśli graf prosty G ma n
wierzchołków (n ≥ 3) oraz suma stopni dowolnych dwóch
wierzchołków, które nie są sąsiednie, jest większa od n, to
graf G jest hamiltonowski.
Zagadnienie najkrótszej drogi
B
D
G
J
E
A
C
F
H
I
L
K
Graf z wagami
liczba przypisana krawędzi - waga
Litery oznaczają miasta połączone drogami.
Liczby oznaczają długości dróg lub czas podróży, lub koszt przejazdu.
Znaleźć drogę z miasta A do miasta L o najmniejszej
całkowitej wadze.
Matematyka Dyskretna, Podstawy Logiki i Teorii Mnogości
Barbara Głut
11
Przesuwamy się wzdłuż grafu z lewa na prawo, przypisując każdemu
wierzchołkowi V liczbę l(V) określającą najkrótszą odległość od
wierzchołka A do wierzchołka V.
B
D
G
J
E
A
C
H
I
F
L
K
Zagadnienie chińskiego listonosza
Zadanie polega na tym, by listonosz, który musi doręczyć pocztę,
przeszedł jak najkrótszą łączną drogę i powrócił do punktu wyjścia.
B
C
A
D
F
E
Znaleźć taką trasę zamkniętą, której całkowita waga jest minimalna i
w której każda krawędź występuje co najmniej jeden raz.
Jeśli graf jest grafem eulerowskim, to każdy cykl Eulera jest poszukiwaną
trasą.
Jeśli graf nie jest eulerowski – zadanie trudniejsze.
Matematyka Dyskretna, Podstawy Logiki i Teorii Mnogości
Barbara Głut
12
B
C
A
D
F
Wierzchołki B i E są jedynymi
wierzchołkami stopni nieparzystych
→ znajdujemy ścieżkę półeulerowską
z B do E.
Aby powrócić najkrótszą drogą do
punktu wyjścia → znajdujemy
najkrótszą drogę z E do B.
E
Rozwiązanie:
znaleziona ścieżka półeulerowska
+ najkrótsza droga E→ F → A → B
razem tworzą graf eulerowski =>
B
C
A
D
Droga długości: 13 + 64 = 77
F
E
Zagadnienie komiwojażera
Komiwojażer, który chce odwiedzić kilka miast i powrócić do punktu
wyjścia, powinien znaleźć drogę o najmniejszej łącznej długości.
A
E
B
C
D
Znaleźć cykl Hamiltona o najmniejszej całkowitej wadze.
Matematyka Dyskretna, Podstawy Logiki i Teorii Mnogości
Barbara Głut
13