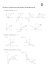Funkcje wielu zmiennych

Automatyka i robotyka
semestr I
rok ak. 2009/2010
Matematyka – ćwiczenia
Funkcje wielu zmiennych
♦ Opis, wykresy i ciągłość
4.1. Znaleźć dziedzinę naturalną (obszar określoności) funkcji:
y
(x2 + y 2 − 4)(9 − x2 − y 2 ); (c) z(x, y) = arc sin ;
x
√
√
x
x
+
y
(d) z(x, y) = arc cos
; (e) z(x, y) = 1 − x2 + y 2 − 1;
(f ) f (x, y) =
.
x+y
x−y
4.2. Narysować plan poziomicowy wykresu funkcji:
(a) z(x, y) = x +
√
y;
(b) z(x, y) =
q
(a) z = xy;
(b) z = 2x − y + 1;
√
(d) z = − 9 − y 2 ;
(e) z = e−x
2 −y 2
;
(c) z = |x| + y;
(f ) f (x, y) = x2 + y.
4.3. Narysować wykres funkcji:
(a) f (x, y) = 25 −
(c) z =
√
x2 y 2
− , gdzie 0 ¬ x ¬ 10, 0 ¬ y ¬ 10; (b) z = −x − y + 1;
4
4
1 − x2 − y 2 na obszarze jej określoności;
(d) z = 0,
(e) f (x, y) = 4 − x2 − y 2 , gdzie 0 ¬ x ¬ 2, 0 ¬ y ¬ 2;
(f ) z = x2 + y 2 , gdzie 0 ¬ x ¬ 5, 0 ¬ y ¬ 5.
4.4. Znaleźć zbiory punktów ciągłości podanych funkcji:




√





 sin x
1 − x2 − y 2 dla x2 + y 2 ¬ 1,
(a) f (x, y) =
(b) g(x, y) =






 0
 1
dla x2 + y 2 > 1;
dla y ­ 0 oraz x ∈ R,
dla y < 0 oraz x ∈ R.
♦ Pochodne cząstkowe i kierunkowe funkcji wielu zmiennych
4.5. Obliczyć wszystkie pochodne cząstkowe pierwszego rzędu podanych funkcji:
1 − xy
x
(a) f (x, y) = arc tg
;
(b) f (x, y, z) = 2
;
x+y
x + y2 + z2
(c) g(x, y) = x3 + 2x2 y + 3xy 2 + 4x − 5y + 100; (d) h(x, y, z) = sin(x cos(y sin z));
s
(e) f (x, y) =
x2 y + 3y 2
+ sin(5x + 7y + 5);
5xy − x2 y 5
(g) k(x, y) = arc tg x −
q
y2
(f )
g(x, y) = ln(8x2 y 3 + 7) + tg
+ 1 + ln(x + 2y); (h) h(x, y) = ex
7
2 y2
cos
3x + y
;
7x2 y
5x + y
;
2x − 3y
Automatyka i robotyka
semestr I
(i) f (x, y) =
(j) g(x, y) =
q
√
rok ak. 2009/2010
Matematyka – ćwiczenia
8x2 y + sin x2 + cos(y 2 x3 ) + (8xy 2 − 7x)10 ;
√
5x2 + y 3 − arc sin x2 + 3y + 5exy .
4.6. Obliczyć:
(a)
q
∂f
√
(1, 5), jeżeli f (x, y) = x3 y 3 + y + y;
∂x
(b)
√
∂f
(2, 5), jeżeli f (x, y) = y 2 + 1 − x2 .
∂y
4.7. Obliczyć wszystkie pochodne cząstkowe drugiego rzędu funkcji i sprawdzić, czy pochodne cząstkowe mieszane są równe:
(a) f (x, y) = sin(x2 + y 2 );
1
(b) g(x, y, z) = √ 2
;
x + y2 + z2
(c) h(x, y, z) = ln(x2 + y 4 + z 6 + 1);
(d) f (x, y) = exy .
2
∂ 2u ∂ 2u ∂ 2u
1
4.8. Sprawdzić, czy funkcja u = √ 2
spełnia
równanie
+
+
= 0?
∂x2 ∂y 2 ∂z 2
x + y2 + z2
4.9. Obliczyć gradienty podanych funkcji we wskazanych punktach:
(a) f (x, y) = x2 + y 2 ,
(b) g(x, y, z) = exyz ,
P = (−3, 4);
P = (−1, 1, −1).
4.10. Obliczyć długość gradient funkcji u = x3 + y 3 − 3z w punkcie P (2, 1, 0).
4.11. Obliczyć pochodne kierunkowe podanych funkcji
punkcie P i kierunku ~v :
√w
"
#
1 3
(a) f (x, y) = sin x cos y, P (0, π), ~v = − ,
;
2 2
z−x
6 3 2
(b) f (x, y, z) =
, P (1, 0, −3), ~v = − , , − .
z+y
7 7 7
2
2
4.12. Obliczyć pochodną funkcji z = 2x − 3y w punkcie P0 (1, 0) w kierunku półosi P0 s o kątach
2
π
kierunkowych α = π, β = .
3
6
4.13. Dana jest funkcja f (x, y, z) = x2 + 3xyz + yz 3 . Obliczyć
df
w punkcie P0 (5, 2, 1), jeżeli
ds
wiadomo, że wektor v = [3, 3, 3] jest zgodnie równoległy do półosi P0 s.
4.14. Napisać równania płaszczyzn stycznych do wykresów podanych funkcji we wskazanych punktach wykresu:
√
!
1 3
arc sin x
(a) f (x, y) =
, (x0 , y0 , z0 ) = − ,
, −1 ; (b) f (x, y) = xy , (x0 , y0 , z0 ) = (2, 4, 16).
arc cos y
2 2
8
Automatyka i robotyka
semestr I
rok ak. 2009/2010
Matematyka – ćwiczenia
♦ Różniczka funkcji wielu zmiennych
4.15. Napisać różniczki podanych funkcji we wskazanych punktach:
y
(a) f (x, y) = arc cos , (x0 , y0 ) = (4, 1); (b) f (x, y, z) = xy − z x , (x0 , y0 , z0 ) = (2, 4, 6).
x
4.16. Wykorzystując różniczkę funkcji obliczyć przybliżone wartości podanych wyraże/n:
(a)
√
2, 1 · 8, 05;
(b) 1, 083,96 ;
(c)
sin 1, 49 · arc tg 0, 07
;
22,95
(d)
q
3
(2.93)3 + (4.05)3 + (4.99)3 .
4.17. Wykorzystując różniczkę funkcji obliczyć w przybliżeniu jak zmieni się objętość V walca o
promieniu podstawy R = 1 m i wysokości H = 2 m, jeżeli jego wysokość zwiększymy o 1 cm, a
promień podstawy zmniejszymy o 3 cm?
4.18. Ciśnienie gazu w pewnym procesie technologicznym wyraża się wzorem
p=
100eT
,
V
gdzie T jest temperaturą gazu, a V jego objętością. Aktualne wartości tych parametrów wynoszą
T = 0o C, V = 300 m3 . Objętość gazu wzrosła o 1 m3 . Obliczyć w przybliżeniu, jak należy
zmienić temperaturę gazu, aby jego ciśnienie nie uległo zmianie.
4.19. Przy pomocy menzurki można zmierzyć objętość ciała z dokładnością ∆V = 0.1 cm3 , a przy
pomocy wagi sprężynowej można ustalić jego masę z dokładnością ∆M = 1 g. Objętość ciała
zmierzona tym sposobem wynosi V = 25 cm3 , a masa M = 200 g. Z jaką w przybliżeniu
dokładnością można obliczyć gęstość ρ tego ciała?
4.20. Boki trójkątnego kawałka ziemi zmierzone z dokładnością 1 m wynoszą a = 250 m, b = 400 m.
Kąt między tymi bokami zmierzony z dokładnością 0.01 rad wynosi α =
dokładnością można obliczyć pole P tego kawałka ziemi?
9
π
. Z jaką w przybliżeniu
3