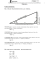Zapisz jako PDF

Funkcje trygonometryczne w trójkącie prostokątnym
Oznaczenia boków i kątów trójkąta
prostokątnego użyte w definicjach
Sinus
Sinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek przyprostokątnej przeciwległej
danemu kątowi do przeciwprostokątnej:
Kosinus
Kosinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek przyprostokątnej przyległej
do danego kąta do przeciwprostokątnej:
Tangens
Tangensem kąta ostrego w trójkącie prostokątnym nazywamy stosunek przyprostokątnej
przeciwległej danemu kątowi do przyprostokątnej przyległej do danego kąta:
Kotangens
Kotangensem kąta ostrego w trójkącie prostokątnym nazywamy stosunek przyprostokątnej
przyległej do danego kąta do przyprostokątnej przeciwległej danemu kątowi:
Uwaga
Czasem, choć rzadko, używa się też funkcji sekans i kosekans. Są one definiowane jako:
.
Miara łukowa kąta
Def. 1 radian (1 rad) jest to miara kąta opartego na łuku, którego długość jest równa długości
promienia okręgu. Mamy więc proste wzory na zamianę miary kąta w stopniach
na miarę łukową
:
W szczególności:
(rad);
;
;
się już nie podaje że jest on mierzony w radianach).
(podając kąt w mierze łukowej, często
Funkcje trygonometryczne dowolnego kąta
Mając zdefiniowane funkcje trygonometryczne dla dowolnego kąta
definicje na dowolny inny kąt. Robi się to tak:
, łatwo rozszerzyć te
Niech będzie kątem skierowanym umieszczonym w ukł wsp. tak, że jego początkowe ramię
pokrywa się z dodatnią półosią
, a końcowym ramieniem jest półprosta o początku w punkcie
. Na końcowym ramieniu wybieramy dowolny punkt
, różny od punktu
Funkcje trygonometryczne kąta
definiujemy w sposób następujący:
gdzie
od punktu
jest odległością punktu
,zaś
.
.
Znaki funkcji trygonometrycznych w poszczególnych ćwiartkach układu
współrzędnych
"W
W
W
A
pierwszej wszystkie są dodatnie,
drugiej tylko sinus,
trzeciej tangens i kotangens,
w czwartej kosinus".
Wartości funkcji trygonometrycznych dla niektórych wartości kątów
stopnie
NI
NI
NI
NI
Wykresy funkcji sinus i cosinus.
Parzystość i nieparzystość funkcji trygonometrycznych
Funkcja
jest parzysta:
Funkcja
jest nieparzysta:
Funkcja
jest nieparzysta:
Funkcja
jest nieparzysta:
Okresowość funkcji trygonometrycznych
Okresem podstawowym funkcji
oraz
Zachodzi:
oraz
Okresem podstawowym funkcji
oraz
Zachodzi:
oraz
jest
:
.
jest :
.
Związki pomiędzy funkcjami trygonometrycznymi tego samego kąta, tzn.
tożsamości trygonometryczne
— jest to tzw. jedynka trygonometryczna;
;
;
Przy użyciu tych tożsamości trygonometrycznych można udowodnić wiele innych — zależnie od
potrzeby.
Związki pomiędzy funkcjami trygonometrycznymi różnych kątów
Dla dowolnych kątów
zachodzą związki:
Dow. Wynikają z nich, po przyjęciu
, związki na funkcje trygonometryczne podwojonego kąta
oraz połówkowego kąta:
Wzory redukcyjne na sprowadzanie kąta do pierwszej ćwiartki
Okresowość funkcji trygonometrycznych oraz wzory na sumę kątów pozwalają sprowadzić dowolny
argument funkcji trygonometrycznej do I. ćwiartki.
Przykład
Funkcje odwrotne do funkcji trygonometrycznych
Z uwagi na okresowość funkcji trygonometrycznych, nie można zdefiniować funkcji odwrotnych do
nich dla wszystkich argumentów. Funkcję odwrotną do można zdefiniować dla tych argumentów,
dla których jest wzajemnie jednoznaczna.
Weźmy funkcję
(+ zbiory, pomiędzy którymi
, widać, że
jest funkcją wzajemnie jednoznaczną, jeśli za zbiór
argumentów weźmiemy
Funkcję odwrotną
działa). Patrząc na wykres
, zaś za zbiór wartości
do funkcji
funkcji odwrotnej — jako: Jeśli
.
nazywamy
i definiujemy — zgodnie z definicją
, to
.
Uwaga
Wzajemna jednoznaczność
ma miejsce także w innych sytuacjach, np. "X
niestandardowy":
,
Standardowa umowa mówi, że za
, i zdefiniować funkcję
bierze się
.
.
Funkcja odwrotna do sinusa
Ostatecznie (aby oswoić z różnymi notacjami):
Def. Dla funkcji
:
definiujemy odwrotną do niej funkcję
jako: Jeśli
, to
itd.).
Wykres funkcji
(więc np.
:
— zgodnie z ogólną reguła uzyskiwania wykresów funkcji odwrotnych — otrzymuje się z wykresu
przez zamianę osi lub równoważnie przez symetrię względem osi
.
Funkcje odwrotne dla innych funkcji trygonometrycznych
Def. Dla funkcji
:
definiujemy odwrotną do niej funkcję
jako: Jeśli
Def. Dla funkcji
:
, to
:
.
definiujemy odwrotną do niej funkcję
jako: Jeśli
,to
:
.
Biegunowy układ współrzędnych
Punkt na płaszczyźnie można zaznaczyć, zadając układ współrzędnych i pisząc współrzędne punktu
(w tym układzie są to też składowe wektora
).
Do wyznaczenia położenia punktu na płaszczyźnie można jednak użyć innego układu współrzędnych.
Jeżeli zamiast
wprowadzimy
przez
Biegunowy układ współrzędnych
(lub na odwrót:
), to jest to równie dobry układ współrzędnych co
Każdemu punktowi płaszczyzny odpowiada dokładnie jedna para liczb
oraz na odwrót: Każdej
parze
odpowiada dokładnie jeden punkt płaszczyzny. (jest jeden WYJĄTEK: punkt
kąt nie jest określony).
, gdzie
Jedną z większych sztuk w matematyce (i fizyce) jest dobór odpowiedniego układu współrzędnych.
Gdy się go odpowiednio (do zagadnienia) dobierze, to problem często znacznie się upraszcza lub
nawet trywializuje.
:
Przykłady
1. Równanie okręgu (o środku w
postać
i promieniu
) ma we współrzędnych kartezjańskich
zaś we współrzędnych biegunowych
2.
Rysunek kardioidy dla a=0.9
Rozważmy krzywą (kardioidę)
Analiza we współrzędnych kartezjańskich, aczkolwiek możliwa, jest dość uciążliwa. We
współrzędnych biegunowych badanie jest o wiele łatwiejsze i krzywą można narysować "od
ręki".
3. Rozważmy krzywą (lemniskata Bernoulliego)
Rysunek wykres leminiskaty Bernoulliego dla a=3
Można ją wykreślić we współrzędnych kartezjańskich, aczkolwiek jest to dość pracochłonne.
We współrzędnych biegunowych ma ona o wiele dogodniejszą do analizy postać:
Twierdzenie kosinusów
Rozpatrzmy trójkąt o bokach długości
, gdzie kąt między bokami i wynosi . Ma miejsce
następujące uogólnienie twierdzenia Pitagorasa, zwane twierdzeniem kosinusów:
Zachodzi:
Ilustracja twierdzenia kosinusów
Twierdzenie sinusów
Rozpatrzmy trójkąt o bokach
oraz kątach: — naprzeciw boku (tzn. kąt pomiędzy bokami
); — naprzeciw boku ; — naprzeciw boku . Między długościami boków
a kątami
zachodzą następujące związki, zwane twierdzeniem sinusów:
Zachodzą równości:
Trójkąt.
gdzie
— promień okręgu opisanego na trójkącie.
i