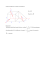1 Powierzchnie stopnia drugiego

Wykład dla semestru 2
1
Małgorzata Komisarska
1
Powierzchnie stopnia drugiego
Powierzchnią stopnia drugiego nazywamy zbiór punktów P (x, y, z), których współrzędne
spełniają równanie:
Ax2 + By 2 + Cz 2 + A1 xy + B1 xz + C1 yz + A2 x + B2 y + C2 z + D2 = 0
gdzie co najmniej jeden ze współczynników A, B, C, A1 , B1 , C1 jest różny od zera.
1.1
Powierzchnie walcowe
Powierzchnią walcową nazywamy zbiór prostych równoległych do danej prostej
i przechodzących przez punkty krzywej K.
Krzywą K nazywamy kierownicą, a proste tworzącymi powierzchni walcowej.
Walec eliptyczny:
Kierownicą jest elipsa o równaniu
x2
a2
+
y2
b2
= 1, leżąca na płaszczyźnie OXY , tworzące są
równoległe do osi OZ.
x2 y 2
+ 2 = 1 dla a > 0, b > 0
a2
b
Podobnie otrzymujemy inne możliwe położenia walca w układzie współrzędnych:
Wykład dla semestru 2
Małgorzata Komisarska
• Kierownicą jest elipsa o równaniu
x2
a2
+
z2
c2
2
= 1, leżąca na płaszczyźnie OXZ, tworzące są
równoległe do osi OY .
x2 z 2
+ 2 = 1 dla a > 0, c > 0
a2
c
• Kierownicą jest elipsa o równaniu
y2
b2
+
z2
c2
= 1, leżąca na płaszczyźnie OY Z, tworzące są
równoległe do osi OX.
y2 z2
+ 2 = 1 dla b > 0, c > 0
b2
c
Walec kołowy:
Jeżeli w równaniu walca eliptycznego a = b = r, otrzymujemy walec kołowy:
Kierownicą jest okrąg o równaniu x2 + y 2 = r2 , leżący na płaszczyźnie OXY , tworzące są
równoległe do osi OZ.
x2 + y 2 = r 2
dla r > 0
Inne położenia walca w układzie współrzędnych:
• Kierownicą jest okrąg o równaniu x2 + z 2 = r2 , leżący na płaszczyźnie OXZ, tworzące są
równoległe do osi OY .
x2 + z 2 = r 2
dla r > 0
Wykład dla semestru 2
Małgorzata Komisarska
3
• Kierownicą jest okrąg o równaniu y 2 + z 2 = r2 , leżący na płaszczyźnie OY Z, tworzące są
równoległe do osi OX.
y 2 + z 2 = r2
dla r > 0
Walec hiperboliczny:
Kierownicą jest hiperbola o równaniu
x2
a2
−
y2
b2
= 1, leżąca na płaszczyźnie OXY , tworzące
są równoległe do osi OZ.
x2 y 2
− 2 = 1 dla a > 0, b > 0
a2
b
Przykładowe położenia w układzie współrzędnych:
• Kierownicą jest hiperbola o równaniu
x2
a2
2
− zc2 = 1, leżąca na płaszczyźnie OXZ, tworzące
są równoległe do osi OY .
x2 z 2
− 2 = 1 dla a > 0, c > 0
a2
c
• Kierownicą jest hiperbola o równaniu
y2
b2
2
− zc2 = 1, leżąca na płaszczyźnie OY Z, tworzące
są równoległe do osi OX.
y2 z2
− 2 = 1 dla b > 0, c > 0
b2
c
Wykład dla semestru 2
Małgorzata Komisarska
4
Walec paraboliczny:
Kierownicą jest parabola o równaniu y 2 = 2px, leżąca na płaszczyźnie OXY , tworzące są
równoległe do osi OZ.
y 2 = 2px dla p 6= 0
Inne możliwości:
• Kierownicą jest parabola o równaniu x2 = 2py, leżąca na płaszczyźnie OXY , tworzące są
równoległe do osi OZ.
x2 = 2py
dla p 6= 0
• Kierownicą jest parabola o równaniu y 2 = 2pz, leżąca na płaszczyźnie OY Z, tworzące są
równoległe do osi OX.
y 2 = 2pz
dla p 6= 0
• Kierownicą jest parabola o równaniu z 2 = 2py, leżąca na płaszczyźnie OY Z, tworzące są
równoległe do osi OX.
z 2 = 2py
dla p 6= 0
• Kierownicą jest parabola o równaniu x2 = 2pz, leżąca na płaszczyźnie OXZ, tworzące są
równoległe do osi OY .
x2 = 2pz
dla p 6= 0
• Kierownicą jest parabola o równaniu z 2 = 2px, leżąca na płaszczyźnie OXZ, tworzące są
równoległe do osi OY .
z 2 = 2px dla p 6= 0
Wykład dla semestru 2
1.2
Małgorzata Komisarska
5
Sfera (powierzchnia kulista)
Sferą (powierzchnią kulistą) o środku S(x0 , y0 , z0 ) i promieniu r, r > 0, nazywamy zbiór
punktów, których odległość od środka S jest równa r:
(x − x0 )2 + (y − y0 )2 + (z − z0 )2 = r2
dla r > 0
W szczególności, gdy x0 = y0 = z0 = 0 otrzymujemy równanie sfery o środku S(0, 0, 0)
i promieniu r:
x2 + y 2 + z 2 = r 2
1.3
Elipsoida
dla r > 0
Wykład dla semestru 2
Małgorzata Komisarska
6
Elipsoidą nazywamy powierzchnię o równaniu
x2 y 2 z 2
+ 2 + 2 = 1 dla a > 0, b > 0, c > 0
a2
b
c
Jest to powierzchnia symetryczna względem wszystkich płaszczyzn, osi i początku układu
współrzędnych.
1.4
Paraboloidy
Paraboloidy eliptyczne:
x2 y 2
+ 2 =z
a2
b
dla a > 0, b > 0
W szczególności, gdy a = b otrzymujemy paraboloidę obrotową:
Wykład dla semestru 2
Małgorzata Komisarska
Inne możliwe położenia w układzie współrzędnych:
y2 z2
+ 2 = x dla b > 0, c > 0
b2
c
x2 z 2
+ 2 =y
a2
c
dla a > 0, c > 0
Paraboloidy hiperboliczne:
x2 y 2
− 2 =z
a2
b
dla a > 0, b > 0
7
Wykład dla semestru 2
Małgorzata Komisarska
Inne możliwe położenia w układzie współrzędnych:
y2 z2
− 2 = x dla b > 0, c > 0
b2
c
x2 z 2
− 2 =y
a2
c
1.5
dla a > 0, c > 0
Hiperboloidy
hiperboloidy jednopowłokowe:
hiperboloidą jednopowłokową nazywamy powierzchnię o równaniu
x2 y 2 z 2
+ 2 − 2 = 1 dla a > 0, b > 0, c > 0
a2
b
c
8
Wykład dla semestru 2
Małgorzata Komisarska
hiperboloidy dwupowłokowe:
hiperboloidą dwupowłokową nazywamy powierzchnię o równaniu
x2 y 2 z 2
+ 2 − 2 = −1 dla a > 0, b > 0, c > 0
a2
b
c
1.6
Stożek eliptyczny
stożkiem eliptycznym nazywamy powierzchnię o równaniu
x2 y 2 z 2
+ 2 − 2 = 0 dla a > 0, b > 0, c > 0
a2
b
c
9
Wykład dla semestru 2
W szczególności, gdy a = b otrzymujemy stożek obrotowy:
Wszystkie zamieszczone ilustracje pochodzą z Wikipedii.
Małgorzata Komisarska
10