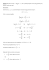Lista 5 - Arsenic Rose

Lista 5
Kamil Matuszewski
18 listopada 2015
Zadanie 1
−xn−1
xn+1 = xn − f (xn ) f (xxnn)−f
(xn−1 ) =
=
xn ·(f (xn )−f (xn−1 ))
f (xn )−f (xn−1 )
f (xn )xn −f (xn−1 )xn −f (xn )xn +f (xn )xn−1
f (xn )−f (xn−1 )
=
−
f (xn )(xn −xn−1 )
f (xn )−f (xn−1 )
=
f (xn )xn−1 −f (xn−1 )xn
f (xn )−f (xn−1 )
A to jest to do czego chcieliśmy dojść. Teraz który wzór jest lepszy? Drugi wzór ma mniejszą liczbę
odejmowań, a jak wiemy z poprzednich list odejmowanie jest niebezpieczne. ALE w momencie
zbliżania się do miejsca zerowego f (xn ) → f (xn−1 ) , czyli wartości te są sobie bardzo bliskie,
podczas gdy w pierwszym wzorze nie mamy takiego problemu, więc, mimo wszystko, drugi wzór
jest gorszy, a pierwszy lepszy.
Zadanie 2
Niech:
F (xk ) = xk+1 , oraz
F (α) = α, F 0 (α) = F 00 (α) = ... = F (i) (α) = ... = F (p−1) (α) = 0, F (p) (α) 6= 0
Wtedy:
F (xk ) = xk+1
\−α
F (xk ) − α = xk+1 − α
Ale nasze xk+1 − α to jakiś błąd, nazwijmy go ek+1 mamy więc:
F (ek + α) − α = ek+1
Rozpiszmy teraz F (ek + α) w szereg Taylora
F (ek + α) = F (α) +
F 0 (α)
1!
· ek + ... +
F (p−1) (α)
(p−1)!
+
· ep−1
k
F (p) (η)
p!
ALE F (α) = α a wszystkie F (i) dla 1 ¬ i < p jest równe 0, dlatego mamy:
α+
ale
F (p) (η)
p!
F (p) (η)
p!
· epk − α =
F (p) (η)
p!
· epk ,
=C
czyli to jest jakaś stała, czyli
en+1 = C · epk
czyli rząd zbieżności to p, a wzór na C to
F (p) (η)
p!
1
· epk
Zadanie 3
Mamy
xn+1 = xn −
f (xn )
.
f 0 (x0 )
Sprawdźmy to daną w poprzednim zadaniu metodą:
F (x) = x −
f (x)
f 0 (x0 )
F (α) = α −
f (α)
,
f 0 (x0 )
ale α to pierwiastek, mamy więc:
F (α) = α −
f (α)
f 0 (x0 )
= α − 0 = α, więc się zgadza.
F 0 (x) = 1 −
f 0 (x)f 0 (x0)
(f 0 (x0))2
F 0 (x) = 1 −
f 0 (x)
f 0 (x0)
F 0 (α) = 1 −
f 0 (α)
f 0 (x0)
Wnioski:
f 0 (x)
Jeśli f 0 (x0)
= 1 to rząd zbieżności ­ 2
W przeciwnym wypadku rząd zbieżności to 1.
Zadanie 4
Mamy
xn+1 = xn −
f (xn )
,
f 0 (xn )
i
f (α) = f 0 (α) = 0 6= f 00 (α)
Podobnie jak w zadaniu 2, odejmijmy obustronnie α i sprawdźmy jak zachowują się błędy.
en+1 = en −
f (en +α)
,
f 0 (en +α)
rozpiszmy teraz górę w szereg Taylora:
e2 ·f 00 (η1 )
2!
0
en+1 = en −
f (α)+ en ·f1! (α) + n
f 0 (en +α)
en+1 = en −
0+0+ n 2! 1
f 0 (en +α)
e2 ·f 00 (η )
en+1 = en −
en (1 − 12 ·
e2n ·f 00 (η1 )
2!·f 0 (en +α)
, ale f (α) = f 0 (α) = 0, więc:
2
00
en ·f (η)
= en − 2!·f
0 (e +α) , i rozpiszmy teraz dół z szeregu Taylora:
n
= en −
f 00 (η1 )
f 00 (η2 ) ).
e2n ·f 00 (η1 )
f 00 (η )
2!·(f 0 (α)+ 1! 2 ·en )
= en −
1
2
·
en ·f 00 (η1 )
0+f 00 (η2 )
=
W przedostatnim przejściu ponownie skorzystaliśmy z tego, że f 0 (α) = 0.Otrzymaliśmy coś dziwf 00 (η )
nego, ale w rzeczywistości f 00 (η1 ) to jakaś (niewielka, tu pomachaj rękoma) stała, co oznacza,
2
że:
en+1 = e1n · C, a to oznacza, że ta metoda jest zbieżna liniowo.
2
Zadanie 5
Wiemy, że
|xn+1 −α|
p
n→inf |xn −α|
lim
lim |en+1p |
n→inf |en |
= C, i, że możemy to zapisać, jako
=C
|en+1 |
p
n→inf |en |
log lim
|
= log C ↔ lim log |e|en+1
p = log C,
n|
n→inf
Ale również, wiemy, że możemy to zapisać jako:
n+2 |
lim log |e|en+1
= log C
|p
n→inf
Czyli, że:
|
n+2 |
= lim log |e|en+1
lim log |e|en+1
p
|p
n|
n→inf
n→inf
lim log
n→inf
|en+2 |
|en+1 |p
lim (log
n→inf
|en+2 |
|en+1 |p
|
− lim log |e|en+1
p = 0
n|
n→inf
|
− log |e|en+1
p ) = 0
n|
lim (log |en+2 | − log |en+1 |p − log |en+1 | + log |en |p ) = 0
n→inf
lim (log |en+2 | − p · log |en+1 | − log |en+1 | + p · log |en |) = 0
n→inf
lim (log |en+2 | − log |en+1 | − p · (log |en+1 | − log |en |)) = 0
n→inf
lim (log |en+2 | − log |en+1 |) − lim p · (log |en+1 | − log |en |) = 0
n→inf
n→inf
p · lim (log |en+1 | − log |en |) = lim (log |en+2 | − log |en+1 |)
n→inf
p = lim
n→inf
n→inf
(log |en+2 |−log |en+1 |)
(log |en+1 |−log |en |)
Zadanie 6
Co się dzieje w 6? Program ma kilka komentarzy, odkomentowanie komentarzy
oznaczonych odpowiednim (i) i zakomentowanie pozostałych da ci inną funkcję.
Zmieniając x od którego zaczynasz i zmieniając wartość a, otrzymujemy różne wyniki, jednak możemy zauważyć, ze dla pierwiastków pojedynczych zbieżność jest
sześcienna a dla pierwiastków podwójnych już liniowa.
3