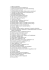iCSE: Zagadnienie dwóch ciał

iCSE: Zagadnienie dwóch ciał
Skrypt
Rozpatrzmy układ dwóch punktowych ciał o masach m1 i m2 , znajdujących się w położeniach r1 i r2 (wektory oznaczone są pogrubioną czcionką)
względem początku układu współrzędnych O. Niech energia ich wzajemnego
oddziaływania U zależy tylko od odległości między nimi: U = U (|r1 − r2 |).
Wówczas Lagrangian tego układu ma postać (kropka nad symbolem oznacza
pochodną po czasie):
L=
m1 ṙ21 m2 ṙ22
+
− U (|r1 − r2 |).
2
2
(1)
Jeśli wprowadzimy następujące oznaczenia na masy:
• całkowita masa układu M :
M = m1 + m2 ,
• masa zredukowana µ:
1
1
1
=
+
,
µ
m1 m2
oraz na wektory:
• wektor opisujący ruch względny ciała 1 względem ciała 2:
r = r1 − r2 ,
• wektor środka masy:
R=
m1
m2
r1 +
r2 ,
M
M
to Lagrangian (1) można zapisać w postaci:
L=
M Ṙ2 µṙ2
+
− U (|r|) = LR + Lr ,
2
2
1
(2)
m1
r
R
r1
m2
r2
O
Rysunek 1: Przykładowy układ wektorów r1 i r2 oraz mas m1 < m2 . Rozpatrzmy następnie rzeczywisty układ: m1 = mZ oraz m2 = mS , gdzie mZ
to masa Ziemi, a mS to masa Słońca. Zakładając, że orbita Ziemska jest
okręgiem o promieniu wielkości jednej jednostki asronomiczej (1 AU), którego środek leży w środku Słońca oraz przyjmując ten środek za początek
układu współrzędnych (tj. r = r1 , |r| = 1AU, r2 = 0), otrzymamy: µ ≈ mZ ,
M ≈ mS oraz |R| < RS , gdzie RS to promień Słońca (środek masy rozpatrywanego układu leży wewnątrz Słońca).
Przystąpmy następnie do analizy równań ruchu Lagrange’a:
M Ṙ2
(3)
2
opisuje ruch środka masy układu dwóch ciał – jest to ruch cząstki swobodnej
o masie M – ruch prostoliniowy i jednostajny,
LR =
µṙ2
− U (|r|)
(4)
2
opisuje ruch względny jednego ciała względem drugiego – jest to ruch cząstki
o masie µ w polu zewnętrznym U (|r|).
Lr =
Zatem ruch dwóch ciał możemy sprowadzić do ruchu układu jako całości
oraz ruchu względnego. Jeżeli wybierzemy układ odniesienia związany ze
środkiem masy układu dwóch ciał to wówczas R = 0. Układ dwóch ciał jako całość spoczywa w tym układzie odniesienia i to w początku tego układu.
Początek układu współrzędnych znajduje się zatem w środku masy układu
ciał.
Zajmijmy się zatem ruchem opisanym Lagrangianem Lr – jest to ruch
ciała w polu o symetrii sferycznej. Jeżeli energia potencjalna punktu U materialnego zależy tylko od odległości od pewnego nieruchomego punktu w
2
przestrzeni, jak w naszym przypadku, to pole takie nazywa się polem centralnym. Siła działająca na ten punkt materialny wynosi:
F = −grad U (r) = −
∂U (r)
∂U (r)
∂U (r)
ex −
ey −
ez ,
∂x
∂y
∂z
gdzie: r = xex + yey + zez , r = |r| =
p
x2 + y 2 + z 2 .
Obliczając odpowiednie pochodne:
∂U (r) ∂r
∂U (r) x
∂U (r)
=
=
,
∂x
∂r ∂x
∂r r
podobnie dla y i z,
otrzymujemy, że F ma taki sam kierunek jak r :
F=−
∂U (r) r
.
∂r r
Użyjmy następnie powyższych obliczeń do pokazania, że w polu centralnym
zachowany jest moment pędu J = r × p względem centrum (źródła pola):
J̇ = ṙ × p + r × ṗ
= v × mv + r × F
∂U (r) r
= 0,
= 0+r× −
∂r r
przy czym w naszym przypadku m = µ. Ponieważ J jest stały i prostopadły
do promienia wodzącego r i prędkości cząstki v, więc ruch odbywa się w
płaszczyźnie prostopadłej do J, czyli jest to ruch płaski.
Dalszą dyskusję będziemy prowadzili w układzie sferycznym – przepiszmy
zatem Lagrangian Lr w tym układzie:
1
Lr = µ(ṙ2 + r2 θ̇2 + r2 sin2 θφ̇2 ) − U (r) .
2
(5)
Zgodnie z naszymi poprzednimi rozważaniami (rozpatrywany ruch jest ruchem płaskim) z r, θ, φ trzeba wybrać dwie współrzędne. Jeżeli ustalimy
θ = π/2 to ruch będzie odbywać się w płaszczyźnie (x, y), a J będzie skierowany wzdłuż osi z : J = Jez . wówczas Lagrangian Lr uprości się do (θ̇ = 0,
sin θ = 1):
1
Lr = µ(ṙ2 + r2 φ̇2 ) − U (r) .
(6)
2
Równanie ruchu cząstki r = r(φ) otrzymamy rozwiązując układ równań
Lagrange’a:

∂Lr
d ∂Lr


−
= 0


 ∂r
dt ∂ ṙ
(7)


∂L
d
∂L
r
r


−
= 0

∂φ
dt ∂ φ̇
3
Drugie z równań (7) daje nam J˙ = 0 :
µr2 φ̇ = J .
(8)
Z pierwszego z równań (7) otrzymamy:
µ(r̈ − rφ̇2 ) = Fr ,
(9)
gdzie: Fr = −∂U (r)/∂r to radialna składowa siły. Obliczmy następnie (φ̇ =
J/µr2 ):
J ∂ 1
dr
∂r
∂r J
=−
,
ṙ =
=
φ̇ =
dt
∂φ
∂φ µr2
µ ∂φ r
podobnie, korzystając z powyższego wyniku, obliczamy:
r̈ =
dṙ
J 2 ∂2
=− 2 2 2
dt
µ r ∂φ
1
r
.
Stosując wyniki powyższych obliczeń do (9) otrzymujemy wzór Bineta:
∂2
∂φ2
1
r
+
1
µr2
= − 2 Fr .
r
J
(10)
Z równania (10), zakładając U (r) = −α/r (wtedy Fr = −α/r2 ), znajdujemy
tor cząstki r = r(φ) (krzywe stożkowe):
p
=r
1 + e cos(φ − φ0 )
gdzie: p = J 2 /(µα), e =
√
(11)
1 + 2Ep to mimośród:
e = 0
okrąg,
e < 1
elipsa,
e = 1
parabola,
e > 1
hiperbola.
Występujący w definicji e symbol E oznacza całkowitą energię układu:
E =
=
=
∂Lr
∂Lr
ṙ +
φ̇ − Lr
∂ ṙ
∂ φ̇
1
µ(ṙ2 + r2 φ̇2 ) + U (r)
2
1 2
J2
µṙ +
+ U (r) .
2
2µr2
Rozpatrywany przez nas układ ma dwie całki ruchu: J˙ = 0 oraz Ė = 0.
4
Zadania
Zadanie 1. Sprawdź przejście i ) z (1) do (2), a następnie ii ) z (4) do (5).
Zadanie 2. Oblicz składowe wektora momentu pędu J w układzie sferycznym, porównaj uzyskany wynik z (8).
Zadanie 3. Sprawdź, że (11) jest faktycznie
rozwiązaniem (10) dla dowol√
nego e (tzn. niekoniecznie dla e = 1 + 2Ep).
5