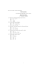∞= limn −∞= − )23(limn .ln ) ), cos( ) ,2 ), ! 1 ), )1( 12 ), ) n af n ae ad

Analiza matematyczna 1
Lista 2
Z.1.
Korzystając z definicji granicy ciągu wykazać, że (po 3 p.)
n
= 1,
n→∞ n + 1
a) lim n n = 1 ,
c) lim n 5 = 1 ,
b) lim
n→∞
n→∞
(−1) n
= 0,
n→∞
n
d) lim
e) lim n 2 = ∞ , f) lim(3 − 2n ) = −∞ .
n→∞
n→∞
Z.2. Zbadać monotoniczność ciągów o następujących wyrazach ogólnych: (po 2 p.)
a ) an = n 2 ,
b) a n =
2n + 1
n2 + 1
, c ) an =
, d ) an = 2 n , e) an = cos(nπ ),
n(n + 1)
n!
f ) an = ln n.
Z.3. Zbadać czy ciągi o następujących wyrazach ogólnych są ograniczone z dołu, z góry, czy są
ograniczone: (po 2 p.)
1
3n
1
a ) an = , b ) a n = n
, c) an = n + 2 , d ) an = ln n, e) an = 2 − .
n
3 +2
n
Z.4. Obliczyć granice ciągów o następujących wyrazach ogólnych : (po 2 p.)
4n − 3
n2 −1
(2n − 1) , d) a = 2 − 5n − 10n 2 .
c
a
=
, b ) an =
,
)
n
n
(4n − 1)(3n + 2)
6 − 5n
3 − n3
3n + 15
2
a ) an =
Z.5. Niech a0 ,..., ak , b0 ,..., bl ∈ R , przy czym ak , bl ≠ 0 . Oblicz
ak n k + ... + a1n + a0
. (3p.)
n→∞ b n l + ... + b n + b
l
1
0
lim
Z.6. Obliczyć granice ciągów o następujących wyrazach ogólnych : (po 2 p.)
a ) a n = n 2 + n − n, b) a n = 3n 2 + 2n − 5 − n 3 , c) an = 3 n 3 + 4n 2 − n,
d ) an =
1
n + n +1 − n + 5
2
2
, e) a n =
1
3
n + n + 1 − 3 n3 − n 2 + 1
3
2
,
f ) an =
3n − 2 n
4 ⋅ 32 n − 7
2 n +1 − 3n −2
1 + 2 + 3 + ... + n
,
g
)
a
,
h
)
a
=
, i ) an =
,
=
n
n
n
n
n
n+2
n2
4 −3
5⋅9 + 2
3
j ) an =
12 + 2 2 + ... + n 2
1 + 3 + 5 + ... + (2n − 1)
1 + 2 + 4 + ... + 2n
, k ) an =
, l) an =
.
3
3
n
7n + n − 1
(3n − 1) 2
Z.7. Obliczyć granice ciągów o następujących wyrazach ogólnych : (po 2 p.)
a ) an =
n
1 + 2 + 3 + ... + n
n sin n
sin(2n), b) an =
cos(n !), c) an = 2
.
3
n +1
n
n +1
2
(Wykorzystać fakt : Jeżeli ciąg (an ) jest ograniczony, zaś ciąg (bn ) jest zbieżny do zera, to ciąg
(anbn ) jest zbieżny do zera )
Z.8. Obliczyć granice ciągów o następujących wyrazach ogólnych : (po 2 p.)
sin 2 n + 4n
 3  1 1
a ) a n = 5 + 4 + 3 , b) a n =   +   +   , c ) an =
, d ) an = n 2n 4 + n 2 + 1,
3n − 1
 4  2 3
n
n
n
n
n
n
n
n
1
e) an = n 14n 2 − 2n + 6 ,
n
 2
i ) an = 1 +  ,
 n
f ) an = n 2 n + π n + e n ,
 1  n  3  n  n
g ) an = n 5 n + cos 2 n + 3n , h) an =   +    ,
 3   4  
 n +5
 4
j ) an = 
 , k ) a n = 1 − 
 n 
 n
n
6n
2n
1 

 2n − 1 
n ) a n = 1 +
 , o) an = 
 ,
 2n + 3 
 2n + 1 
− n +3
n2
 n2 + 6 
1 

, l ) an = 1 − 2  , m) an =  2  ,
 n 
 n 
n
2n
 3n − 2 
p ) an = 
 .
 3n + 1 
Z.9. Zbadaj zbieżność ciągu (an ) n∈N stwierdzając, czy jest monotoniczny i ograniczony: ( 9p.)
a ) a1 = 0, an+1 = 2 + an dla każdego n ∈ N ,
b) a1 =
π
2
, an+1 = sin an dla każdego n ∈ N ,
c) a1 = a2 = 1, an+ 2 = an + an+1 dla każdego n ∈ N 0 .
Z.10 .Zbadaj zbieżność ciągu (an ) n∈N stwierdzając czy spełnia on warunek Cauchy’ego: (po 3
p.)
a ) an =
sin 1 sin 2
sin n
+ 2 + ... + n ,
2
2
2
b ) an = 1 +
1
1
1
+ 2 + ... + 2 ,
2
2 3
n
c ) an = 1 +
1 1
1
+ + ... + .
2 3
n
Z.11. Oblicz granice dolną i górną ciągu (an ) n∈N : (po 2 p.)
a ) an = (−1) n ,
b) an = (−3) n ,
c) an = sin
nπ
,
2
d ) an = cos
e) an = tg
nπ
,
3
nπ
.
3