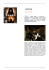kwartalna sprzedaż żelazek

Modele nieliniowe
MODELE NIELINIOWE
Przykład. (model liniowy i nieliniowy - porównanie).
Kwartalna sprzeda elazek w latach 1996 - 1999 wynosiła:
t
yt
1
45
2
53
3
57
4
62
5
64
6
68
7
65
8
68
9
67
10
69
11
72
12
70
13
73
14
75
Wyznacz prognoz na trzeci kwartał roku 1999.
Z wykresu wida , e trend jest rosn cy lecz coraz wolniejszy (wzgl dne nasycenie rynku)
zatem zamiast trendu liniowego nale y zastosowa trend nieliniowy o malej cym tempie
wzrostu np. model pot gowy y = atb (0 < b < 1).
sprzeda (tys. szt.)
Logarytmuj c model pot gowy y = atb otrzymamy lny = lna + blnt a po podstawieniu
t' = lnt; y' = lny; a' = lna otrzymamy model liniowy y' = a' + b't'.
Wykres par (lnt, lny) potwierdza trafno wybranego modelu.
80
75
70
65
60
55
50
45
40
kwartalna sprzeda
elazek
y = 1,8066x + 51,308
R2 = 0,8308
y = 46,783x0,1768
R2 = 0,9609
1
2
3
4
5
6
7
8
9
10 11 12 13 14
kwartały
t
1
lnt
0
lny
2
3
4
5
6
7
8
9
0,69 1,1 1,39 1,61 1,79 1,95 2,08 2,2
10
11
12
13
14
2,3
2,4 2,48 2,56 2,64
3,81 3,97 4,04 4,13 4,16 4,22 4,17 4,22 4,2 4,23 4,28 4,25 4,29 4,32
Oszacowany model liniowy ma posta :
yˆ ′ = 3,846 + 0,177t ′
Oszacowany model pot gowy ma posta :
yˆ = 46,8t 0,177
Zatem prognoza punktowa wyniesie y15 = 46,8 ⋅ 15
Problem: wyznaczy prognoz punktow na 16 kwartał.
*
0,177
1
= 75,6
Modele nieliniowe
Model liniowy wzgl dem parametrów.
Yˆ = b0 + b1 f1 ( X 1 ) + ... + bk f k ( X k )
f1, ..., fk - funkcje ró nowarto ciowe.
Podstawiaj c Zi = fi(Xi)
i = 1, ..., k otrzymamy model liniowy:
Yˆ = b0 + b1 Z1 + ... + bk Z k
Przykład. (model paraboliczny).
Yˆ = b0 + b1 X + b2 X 2
b2 ≠ 0,
podstawiaj c
Z1 = X, Z2 = X2 , otrzymamy model liniowy
Yˆ = b0 + b1 Z1 + b2 Z 2
Przykład. (model hiperboliczny).
b
Yˆ = b0 + 1
X
X >0
b1 ≠ 0,
podstawiaj c
Z = 1/X, otrzymamy model liniowy
Yˆ = b0 + b1 Z1
Przykład. (model logarytmiczny).
Yˆ = b0 + b1 ln X
X >0
podstawiaj c
Z = lnX, otrzymamy model liniowy
Yˆ = b0 + b1 Z 1
2
b1 ≠ 0,
Modele nieliniowe
Model linearyzowany.
Model linearyzowany to taki model dla którego istnieje jednoznaczne przekształcenie
obu jego stron takie, e otrzymamy model liniowy lub liniowy wzgl dem parametrów.
Przykład. (model wykładniczy).
Yˆ = b0 p b1 X
b0, p > 0, p ≠ 1
ogólnie
Yˆ = b0 p b1 X1 +...+bk X k
Linearyzacja polega na obustronnym zlogarytmowaniu modelu wyj ciowego (najlepiej
zastosowa logarytm o podstawie p) i podstawieniu
~
b0 = log p b0 ,
otrzymamy model liniowy
Zˆ = log p Yˆ ,
~
Zˆ = b0 + b1 X 1 + ... + bk X k
Przykład. (model pot gowy).
Yˆ = b0 X b1
b0, X > 0,
ogólnie
b
b
b
Yˆ = b0 X 1 1 X 2 2 ... X k k
Linearyzacja polega na obustronnym zlogarytmowaniu modelu wyj ciowego (najlepiej
zastosowa logarytm naturalny - o podstawie e) i podstawieniu
~
b0 = ln b0 , Z i = ln X i ,
otrzymamy model liniowy
Zˆ = ln Yˆ ,
~
Zˆ = b0 + b1 Z1 + ... + bk Z k
3
Modele nieliniowe
Estymacja parametrów funkcji regresji krzywoliniowej.
Parametry wybranej funkcji nieliniowej wyznacza si te bezpo rednio metod
kwadratów, korzystaj c z odpowiedniego układu równa normalnych.
Funkcja wielomianowa.
najmniejszych
yˆ i = b0 + b1 x + b2 x 2 + ... + bk x k
Jej parametry b0, ...,bk wyznaczamy rozwi zuj c układ równa normalnych który ma posta :
nb0 +
xi b1 +
xi2 b2 + ... +
i
xi b0 +
i
xik +1 bk =
xi3 b2 + ... +
i
yi
i
xi2 b1 +
i
xik bk =
i
i
i
xi yi
i
...
xik +1 b1 +
xik b0 +
i
xik +2 b2 + ... +
i
i
xi2k bk =
xik yi
i
i
Powy szy układ k + 1 równa otrzymujemy przyrównuj c do zera pochodne cz stkowe funkcji k + 1 zmiennych
S (b0 , b1 , b2 ,..., bk ) =
n
i =1
( yi − yˆi )2 =
n
i =1
(y − (b
i
0
+ b1 xi + b2 xi2 + ... + bk xik
))
2
W szczególno ci funkcja kwadratowa.
yˆ i = b0 + b1 x + b2 x 2
Jej parametry b0, b1, b2 wyznaczamy rozwi zuj c układ równa normalnych który ma posta :
nb0 +
xi b1 +
xi2 b2 =
i
i
i
xi b0 +
xi2 b0 +
yi
i
xi2 b1 +
i
i
i
i
xi3 b1 +
i
xi3 b2 =
xi yi
i
xi4 b2 =
xi2 yi
i
Funkcja pot gowa.
b
yˆ i = axi
Zało enie a > 0, b > 0, xi >0.
Chocia jest to niekiedy szczególny przypadek funkcji wielomianowej to warto rozpatrywa go
równie oddzielnie. Jej parametry a, b wyznaczamy przez przekształcenie do postaci liniowej
(logarytmujemy obie strony).
ln yˆ i = ln a + b ln xi
Układ równa normalnych ma posta :
ln y i = n ln a + b
i
ln xi ln yi = ln a
i
ln xi
i
ln xi + b
i
ln 2 xi
i
Rozwi zuj c powy szy układ równa (liniowych wzgl dem a' = lna i b) obliczamy a' i b.
a'
St d a = e .
Parametr b jest interpretowany jako współczynnik elastyczno ci, tzn. je li zmienna X wzro nie o 1%,
to Y zmieni si rednio o b %.
4
Modele nieliniowe
Funkcja wykładnicza.
yˆ i = ab xi
Zało enie a > 0, b > 0.
Logarytmuj c obie strony otrzymamy.
ln yˆ i = ln a + xi ln b
Układ równa normalnych ma posta :
ln y i = n ln a + ln b
i
xi ln y i = ln a
i
xi
i
xi + ln b
i
xi
2
i
Rozwi zuj c powy szy układ równa (liniowych wzgl dem a' = lna i b' = lnb) obliczamy a' i b'. St d
a = ea' i b = eb'.
Parametr b jest interpretowany jako redni przyrost wzgl dny, tzn. je li zmienna X wzro nie
o jednostk , to Y zmieni si rednio o (b - 1)100 %.
Funkcja logistyczna.
yˆ i =
a
1 + be −ct
gdzie t - czas, a > 0, b > 1, c > 0.
Funkcja logistyczna słu y mi dzy innymi do opisu i prognozowania wielko ci sprzeda y produktu
wchodz cego na rynek.
Przyjmujemy
zt =
1
yt
Najpierw wyznaczamy warto ci parametrów a, c
a=
u
−1
u0
c = − ln
u1
u
gdzie
u = (n − 1)
n −1
z −
t =1
u0 =
n −1
t =1
z t +1
u1 = (n − 1)
n −1
n −1
t =1
n −1
t =1
2
t
t =1
z t2 −
n −1
t =1
z t z t +1 −
2
zt
zt
n −1
t =1
n −1
t =1
z t z t +1
z t +1
n −1
t =1
zt
Nast pnie korzystaj c z obliczonych a i c obliczamy b
b=
1
n
n
t =1
a
− 1 e ct
yt
t = 1, 2, ...,n
Parametr b > 1 gwarantuje istnienie punktu przegi cia, za parametr a jest interpretowany jako poziom
nasycenia (asymptota pozioma).
5
Modele nieliniowe
Uwaga.
a)
W przypadku nieliniowym miar
współczynnik korelacji krzywoliniowej
n
R = 1− i=n1
i=1
dopasowania
(yi − yˆ)2
(yi − y)
modelu do danych statystycznych jest
R ∈ <0, 1>.
;
2
b)
Bł d prognozy dla modelu nieliniowego przekształconego do modelu liniowego za pomoc
przekształcenia y' = f(y) gdzie f - funkcja ró niczkowalna wyra a si wzorem
Se 1 +
(xτ − x )2
n
(xi − x )2
i =1
Sτ =
W szczególno ci gdy
1
+
n
dy ′ *
yτ
dy
dy ′ * 1
yτ = *
dy
yτ
′
dy *
−1
yτ =
2
dy
yτ*
*
dy ′ *
yτ = e yτ
dy
y' = lny to
y' = 1/y to
( )
y' = ey to
c)
Przykład.
Maj c dane
t
1
2
3
4
5
6
7
8
y
8
6
5
2
2
4
7
8
Wyznaczymy kwadratow funkcj regresji.
Korzystaj c z sum w poni szej tabeli układamy układ równa normalnych:
suma
t
y
t
2
t
3
t
4
y
2
ty
ty
1
8
1
1
1
64
8
8
2
6
4
8
16
36
12
24
3
5
9
27
81
25
15
45
4
2
16
64
256
4
8
32
5
2
25
125
625
4
10
50
6
4
36
216
1296
16
24
144
7
7
49
343
2401
49
49
343
8
8
64
512
4096
64
64
512
36
42 204
1296
8772 262 190 1158
6
2
Modele nieliniowe
a⋅8772 + b⋅1296 + c⋅204 = 1158
a⋅1296 + b⋅204 + c⋅36 = 190
a⋅204 + b⋅36 + c⋅8 = 42
Rozwi zaniem (przybli onym) układu jest
a = 0,4643; b = -4,1548;
c = 12,107
Zatem funkcja regresji kwadratowej ma posta
yˆ = 0,4643x 2 - 4,1548x + 12,107
Funkcja ta jest dobrze dopasowana do danych statystycznych
(R2 = 0,8732, r = 0,93).
Zauwa my,
e w tym przypadku funkcja liniowa nie jest dobr
funkcj
regresji
a bardzo niska warto współczynnika korelacji Pearsona wiadczy o braku zale no ci liniowej a nie
o braku zale no ci jakiejkolwiek.
y = 0 ,4 6 4 3x 2 - 4 ,1 54 8 x + 1 2 ,1 07
R 2 = 0 ,8 7 32
10
8
Y
6
4
2
0
0
2
4
6
czas t
8
10
y = 0 ,0 2 4 x + 5,1 4
R 2 = 0 ,0 00 6
L. Kowalski, 18.03.2005
7