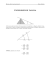v wyszukiwania

Problem (okienkowanie)
Okienkowanie
(windowing)
Wykład 11
2007/01/03
Problem (proste okienkowanie)
Dane:
• zbiór odcinków S na płaszczyźnie, każdy
odcinek poziomy lub pionowy
Cel:
• utworzenie struktury danych pozwalającej
szybko odpowiadać na zapytania z zakresu
Zapytanie z zakresu:
• dane: okno W= [x1,y1]×[x2,y2]
• wynik: wszystkie odcinki s∈S takie, że
s ∩W≠∅
Dane:
• zbiór odcinków S na płaszczyźnie
Cel:
• utworzenie struktury danych pozwalającej
szybko odpowiadać na zapytania z zakresu
Zapytanie z zakresu:
• dane: okno W= [x1,y1]×[x2,y2]
• wynik: wszystkie odcinki s∈S takie, że
s ∩W≠∅
Proste okienkowanie a zapyt. przedz.
Jak znajdować odcinki s∈S, takie że co
najmniej jeden koniec s należy do W?
Odp.: drzewa przedziałowe dla zbioru końców
odcinków
Wydajność:
• pamięć O(n log n)
• preprocessing: O(n log n)
• czas zapytań O(log n + k) – fractional casc.
[O(log2n + k)]
Proste okienkowanie c.d.
Co z odcinkami, których końce poza S?
• interesują nas tylko takie, które przecinają
S, więc przecinają 2 jego krawędzie (obie
pionowe lub obie poziome)
• ograniczmy się do wyszukiwania odcinków
przecinających jedną krawędź (np.
poziomą)... użyjemy interval trees
Odcinki przecinające prostą
Dane: zbiór odcinków poziomych S
Wynik: struktura danych pozwalająca szybko
odpowiadać na pytania:
• dane: prosta pionowa q
• wynik: wszystkie s∈S takie, że s ∩q≠∅
Odcinki przecinające krawędź
Dane: zbiór odcinków poziomych S
Wynik: struktura danych pozwalająca szybko
odpowiadać na pytania:
• dane: odcinek pionowy q
• wynik: wszystkie s∈S takie, że s ∩q≠∅
Interval trees
Dane: zbiór odcinków poziomych I
Interval tree dla I:
• xmid: mediana zbioru końców odcinków
• Ileft={[xj, x’j] ∈I | x’j<xmid}
• Iright={[xj, x’j] ∈I | x’j>xmid}
• Imid={[xj, x’j] ∈I | xj<xmid< x’j}
Interval trees c.d.
• I=∅: IT(I) jest liściem
• I≠∅: v=root(IT(I)) zawiera
– xmid
– Imid posortowany wg końców
– Imid posortowany wg początków
Interval trees: własności
•
•
•
•
Pamięć: O(n)
Głębokość: O(log n)
Czas konstrukcji: O(n log n)
czas zapytania: O(log n + k), gdzie k to
rozmiar odpowiedzi [liczba odcinków]
• left(v)=IT(Ileft)
• right(v)=IT(Iright)
ConstructIntervalTree(I)
•
•
•
•
If I=∅: zwróć pusty liść, wpp
Utwórz wierzchołek v
Wyznacz xmid, Ileft, Iright, Imid
Dołącz do v:
– Lleft(v): Imid posortowany wg początków
– Lright(v): Imid posortowany wg końców
• left(v) ← ConstructIntervalTree(Ileft)
• right(v) ← ConstructIntervalTree(Iright)
Uwaga: przed konstrukcją sort. odc. wg pocz. i końców
QueryIntervalTree(v, qx)
Dane: v – korzeń IT, qx – wsp. pozioma pionowej
prostej
Jeśli v jest liściem: koniec, wpp
• Jeśli qx<xmid(v)
– wypisz wszystkie odcinki Lleft(v), których lewy
koniec mniejszy od xmid(v)
– QueryIntervalTree(left(v), qx)
• Jeśli qx>xmid(v)
– wypisz wszystkie odcinki Lright(v), których prawy
koniec większy od xmid(v)
– QueryIntervalTree(right(v), qx)
Odcinki przecinające krawędź
Dane: zbiór odcinków poziomych S
Wynik: struktura danych pozwalająca szybko
odpowiadać na pytania:
• dane: odcinek pionowy q
• wynik: wszystkie s∈S takie, że s ∩q≠∅
Jak uogólnić interval trees aby rozwiązać
ten problem?
QueryIntervalTree(v, qx)
Dane: v – korzeń IT, qx – wsp. pionowej prostej
Jeśli v jest liściem: koniec, wpp
• Jeśli qx<xmid(v)
– wypisz wszystkie odcinki Lleft(v), których lewy
koniec mniejszy od xmid(v)
– QueryIntervalTree(left(v), qx)
• Jeśli qx>xmid(v)
– wypisz wszystkie odcinki Lright(v), których prawy
koniec większy od xmid(v)
– QueryIntervalTree(right(v), qx)
Odcinki przecinające krawędź
Rozwiązanie:
• zamiast uporządkowanych list Lleft(v) i
Lright(v) [porządek po początkach/końcach],
w węźle v przechowujemy....
• drzewo przedziałowe (range tree) RT(Imid)
dla zbioru Imid
• a algorytm wyszukiwania zmienia się
następująco:
QueryMIntervalTree(v, qx)
Dane: v – korzeń IT, qx, [qy,q’y]: odcinek pionowy
• Jeśli qx< xmid(v)
– wypisz wynik zapytania , (-∝,qx]×[qy,q’y] na
RT(Imid)
– QueryMIntervalTree(left(v), qx)
• Jeśli qx> xmid(v)
– wypisz wynik zapytania , [qx, +∝), ×[qy,q’y] na
RT(Imid)
– QueryMIntervalTree(right(v), qx)
Interval trees: własności po modyf.
•
•
•
•
Pamięć: O(n log n)
Głębokość: O(log n)
Czas konstrukcji: O(n log n)
czas zapytania: O(log2 n + k), gdzie k to
rozmiar odpowiedzi [liczba odcinków]
bez fractional cascading: O(log3 n + k)
Drzewa priorytetowe
Dane: zbiór punktów na płaszczyźnie P.
Drzewo priorytetowe T dla P:
• Jeśli P= ∅: T jest pustym liściem, wpp
•
•
•
•
•
pmin ← punkt w P o min. wart. wsp. x
ymid ← mediana współrzędnych y w P
Pbelow ← {p∈P\{pmin} | p.y < ymid }
Pabove ← {p∈P\{pmin} | p.y > ymid }
T składa się z:
– korzenia v, w nim: p(v)=pmin i y(v)=ymid
– left(v), right(v): drzewa priorytetowe dla Pbelow i
Pabove.
Drzewa priorytetowe
Cel: konstrukcja struktury danych, która dla
• zbioru punktów S
pozwala szybko odpowiadać na zapytania
przedziałowe postaci:
(-∝,qx]×[qy,q’y]
i zajmuje małą (liniową) pamięć.
Wyszukiwanie wg wsp. x
ReportInSubtreeX(v,qx)
Dane: v, korzeń PT (priority tree), qx – liczba.
Wynik: wszystkie p-ty o wsp. x mn. od qx
Jeśli v nie jest liściem i p(v).x < qx:
• Wypisz p(v)
• ReportInSubtreeX(left(v), qx)
• ReportInSubtreeX(right(v), qx)
SearchPrioTree (T, R=(-∝,qx]×[qy,q’y])
Dane: T: drzewo PT; (-∝,qx]×[qy,q’y]: przedział.
Wynik: wszystkie p-ty w prostokącie R
• path1: ścieżka wyszukiwania dla qy (wg pól y(∗
∗))
• path2: ścieżka wyszukiwania dla q’y (wg pól y(∗
∗))
• vsplit: najniższy wspólny element path1 i path2
• Dla każdego v∈path1, poniżej vsplit:
Drzewa priorytetowe: wydajność
• Pamięć: O(n)
• Czas konstrukcji: O(n log n)
• czas odpowiedzi na zapytania
(-∝,qx]×[qy,q’y]: O(log n + k)
– jeśli path1 skierowana w lewo od v:
• ReportInSubtreeX(right(v), qx)
• Dla każdego v∈path2, poniżej vsplit:
– jeśli path2 skierowana w prawo od v:
• ReportInSubtreeX(left(v), qx)
Drzewa segmentowe (segment trees)
Cel (właściwy):
• struktura danych do zadania okienkowania
(zapytania o zakres/prostokąt dla zbioru
odcinków)
Cel pośredni (raz jeszcze):
• Dane: zbiór przedziałów
I={[x1,x’1],...,[xn,x’n]}
• Cel: utworzenie struktury do zapytań o punkt qx:
– odpowiedź to wszystkie przedziały z I
zawierające qx
Drzewa segmentowe
Dane: zbiór przedziałów
I={[x1,x’1],...,[xn,x’n]}
Definicja drzewa segmentowego dla I:
• p1≤… ≤pm: uporządkowany zbiór wszystkich
końców odcinków z I
• przedziały elementarne:
(-∝,p1),[p1,p1], (p1,p2), [p2,p2],…,
(pm-1,pm),[pm,pm],(pm, +∝)
cdn ...
Drzewa segmentowe: definicja c.d.
Drzewo segmentowe – zbalansowane BST:
• liść: reprezentuje przedział elementarny,
• wierzchołek wewnętrzny: reprezentuje przedział sumę przedziałów elementarnych z poddrzewa,
• w każdym wierzchołku przechowujemy:
– Int(v) – przedział odpowiadający wierzchołkowi v,
– I(v)={[x,x’]∈I | Int(v)⊆[x,x’] oraz Int(parent(v))⊄[x,x’]}
Drzewo segmentowe: wyszukiwanie
Dane: v - korzeń drzewa, qx – liczba
Wynik: wszystkie przedziały zawierające qx
QuerySegmentTree(v,qx)
1. Wypisz wszystkie elementy I(v)
2. Jeśli v nie jest liściem:
•
Jeśli qx∈Int(left(v))
•
PAMIĘĆ: O(n log n)
Lemat. Każdy przedział może wystąpić co najwyżej
dwukrotnie w I(∗
∗) na tym samym poziomie.
Drzewo segmentowe: konstrukcja
• Posortuj zbiór {x1,…,xn} ∪ {x’1,…,x’n} i utwórz
przedziały elementarne
• Zbuduj T - zbalansowane BST dla przedziałów
elementarnych i wyznacz bottom-up wartości
Int(v) dla każdego v∈T
• Dla każdego [x:x’] ∈ I
– InsertSegmentTree(root(T), [x:x’])
•
QuerySegmentTree(left(v), qx)
w przeciwnym przypadku
•
QuerySegmentTree(ritht(v), qx)
InsertSegmentTree(v, [x:x’])
Dane: v - korzeń drzewa [w nim wszystkie przedz.el.]
Wynik: [x:x’] wstawione do odpowiednich I(v’)
• Jeśli Int(v) ⊆ [x:x’]:
– dodaj [x:x’] do I(v),
• w przeciwnym przypadku
– Jeśli Int(left(v))∩[x:x’]≠∅:
• InsertSegmentTree(left(v), [x:x’])
– Jeśli Int(ritht(v))∩[x:x’]≠∅:
• InsertSegmentTree(right(v), [x:x’])
Drzewa segmentowe: wydajność
• Pamięć: O(n log n)
• Czas konstrukcji: O(n log n)
• Zapytanie: O(k+log n)
Windowing: nowe drzewa segmentowe
Dane: zbiór odcinków S (zał.: nie przecinają
się)
1. IS: zbiór rzutów odcinków z S na oś OX
2. Zbuduj drzewo segmentowe dla zbioru
odcinków IS, z modyfikacjami:
•
•
Windowing: reprezentacja I(v)
Obserwacja: odcinki w zbiorze I(v)
„rozpinają” obszar odpowiadający Int(v).
Wniosek: odcinki w I(v) można
uporządkować „pionowo” [relacja „nad” i
„pod”]
W efekcie:
T(v) to zbalansowane BST reprezentujące
I(v), wg porządku pionowego.
I(v) reprezentuje odcinki z S, a nie ich rzuty
I(v) dla każdego wierzchołka v
reprezentujemy jako T(v), drzewo binarne
opisane dalej.
Nowe drzewo segm.: wyszukiwanie
Dane: T – nowe drzewo segm.,
U=[qx]×[qy,q’y] – odcinek pionowy
Wynik: zbiór odcinków z T, przecinających U
• wykonaj QuerySegmentTree(T, qx)
• w każdym odwiedzonym węźle v:
a)
b)
c)
d)
nie wypisuj wszystkich elementów T(v)
wyszukaj qy w T(v) [najwyższy poniżej qy]
wyszukaj q’y w T(v) [najniższy powyżej q’y]
wypisz wszystkie odcinki pomiędzy
znalezionymi w (b) i (c)
Nowe drzewo segm.: wydajność
Pamięć: O(n log n)
Czas konstrukcji: O(n log2n) [można O(n logn)
Czas wyszukiwania: O(log2n+k)