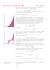TeX: Rola Daniel

262
4) Druga pochodna funkcji xy (w tym samym przedziale) jest równa r(r = 1)xy − 2, widać
stąd, że dla r > 1 i r < 0 funkcja ta jest wypukła, a dla 0 < r < 1 – wklęsła (1) ; itd.
We wszystkich tych przykładach mieliśmy ścisłą wypukłość albo wklęsłość
Na zakończenie wkażemy jeszcze jedną ważną charakterystykę geometryczną funkcji wypukłej f (x). Zamiast cięciwy z wykresu funkcji y = f (x), którą rozpatrywaliśmy
w ustępie 141, rozpatrzmy tu styczną w dowolnym punkcie wykresu (rys. 73).
Twierdzenie 3. Niech funkcja f (x) określona i ciągła w przedziale X ma w tym przedziale
pochodną skończoną f ′ (x). Na to, by f (x) była
wypukła potrzeba i wystarcza, żeby wykres jej leżał całkowicie nad dowolną styczną (lub na tej
stycznej).
K o n i e c z n o ś ć. Styczna do krzywej y =
f (x) w punkcie A0 (x0 , f (x0 )) ma współczynnik
kątowy f ′ (x0 ). Równanie stycznej można zapisać
w następujący sposób:
y = f (x0 ) + f ′ (x0 )(x − x0 ).
Rys. 73
Trzeba wykazać, że wypukłość funkcji f (x) pociąga za sobą dla dowolnych punktów
x0 i x z X nierówność
(10)
f (x) ­ f (x0 ) + f ′ (x0 )(x − x0 ).
Nierówność ta jest równoważna z dwiema nierównościami
(11a)
f ′ (x0 ) ¬
f (x) − f (x0 )
x − x0
dla
x > x0
f ′ (x0 ) ­
f (x) − f (x0 )
x − x0
dla
x < x0
i
(11b)
te zaś nierówności pokrywają się odpowiednio z nierównościami (7a) i (7b) otrzymanymi
przy dowodzie twierdzenia 1 (właśnie przy założeniu wypukłości funkcji), jeśli w pierwszej
z nich przyjąć x2 = x, x1 = x0 , a w drugiej x2 = x0 , x1 = x.
D o s t a t e c z n o ś ć. Załóżmy na odwrót, że spełniona jest nierówność (10) lub, co na
jedno wychodzi, nierówności (11a) i (11b). Wówczas można z nich odtworzyć nierówności
(7a) i (7b), skąd wynika, że f ′ (x1 ) ­ f ′ (x2 ), a więc pochodna f ′ (x) jest funkcją rosnącą.
To zaś, jak wiemy (twierdzenie 1), pociąga za sobą z kolei wypukłość funkcji f (x).
Uwaga. Zwracamy uwagę czytelnika na to, że faktycznie (patrz odsyłacz na str. 261)
konieczność nierówności (10) dla danego x0 i dowolnego x 6= x0 została udowodniona przy
założeniu istnienia pochodnej f ′ (x0 ) tylko w tym samym punkcie x0 .
(1) Przykład ten pozwala przy sposobności pokazać, że iloczyn dwóch funkcji wypukłych może nie być
funkcją wypukłą. Tak więc funkcja −x1/3 jest wypukła, podczas gdy jej kwadrat, tzn funkcja x2/3 jest
wklęsła.
263
144. Nierówność Jensena i jej zastosowania. Zgodnie z definicją funkcji wypukłej (patrz
(1)) mamy
f (q1 x1 + q2 x2 ) ¬ q1 f (x1 ) + q2 f (x2 ),
(q1 , q2 > 0, q1 + q2 = 1).
Można udowodnić, że dla funkcji wypukłe zachodzi ogólniejsza nierówność (którą łączymy z nazwiską Jensena):
(12)
f (q1 x1 +q2 x2 +. . .+qn xn ) ¬ q1 f (x1 )+q2 f (x2 )+. . .+qn xn ,
(q1 , q2 , . . . , qn > 0, q1 +q2 +. . .+qn = 1).
dla dowolnych x1 , x2 , ..., xn z przedziału X . Dla n = 2 nierówność ta jest, jak wiemy, słuszna.
Załóżmy teraz, że jest ona słuszna dla pewnego naturalnego n ­ 2 i udowodnimy, że jest ona
słuszna również dla n+1, tzn. że biorąc n+1 wartości x1 , ..., xn , xn + 1 z X i n+1 liczb dodatnich
q1 , ..., qn , qn + 1, których suma równa się jedności, otrzymamy
(13)
f (q1 x1 + q2 x2 + . . . + qn xn + qn+1 xn+1 ) ¬ q1 f (x1 ) + q2 f (x2 ) + . . . + qn f (xn ) + qn+1 f (xn+1 ),
W tym celu zastąpimy sumę dwóch ostatnich składników po lewej stronie xn xn + qn + 1xn + 1
przez jeden składnik
(qn + qn+1 )
qn
qn+1
xn +
xn+1
qn + qn+1
qn + qn+1
Pozwoli nam to skorzystać z nierówności (12) i stwierdzić, że wytażenie znajdujące się po lewej
stronie we wzorze (13) nie przewyższa sumy
q1 f (x1 ) + q2 f (x2 ) + . . . + (qn + qn+1 )f
qn
qn+1
xn +
xn+1
qn + qn+1
qn + qn+1
Pozostaje tylko zastosować do wartości funkcji w ostatnim składniku podstawową nierówność (13).
Tak więc metodą indukcji matematycznej została udowodniona nierówność (12).
Zwykle zamiast czynników qi , których suma równa się jedności, wprowadza się dowolne liczby
dodatnie pi . Przyjmując w nierówności (12)
qi =
pi
,
p1 + . . . + pn
sprowadzamy tę nierówność do postaci
(12⋆ )
f
P
P
px
p f (x )
P i i ¬ Pi i
pi
pi
W przypadku funkcji wklęsłej f znak nierówności trzeba oczywiście zmienić na przeciwny.
Wybierając na różny sposób funkcję f można otrzymać stąd ważne konkretne nierówności –
i przy tym wszystkie z jednego źródło! Przytoczymy przykłady.
1) Niech f (x) = xk , ngdzie x > 0, k > 1 (funkcja wypukła). Otrzymujemy
k P k
P
pi xi
px
Pi i
,
¬ P
pi
czyli
X
pi xi
k
¬
pi
X k−1 X
pi
pi xki .