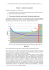
Maksymalna doskonałość

Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Samolotów i Śmigłowców
Projekt 1 – Wyprowadzenie wzorów
Niniejszy dokument zawiera wyprowadzenia wzorów używanych przy wstępnych
szacunkach oraz do określenia podstawowych danych geometrycznych samolotu i
charakterystyk zespołów napędowych. Podane wzory są w większości wynikiem
uproszczonych analiz (przyjętych modeli) i mogą różnić się od tych, które są prezentowane na
wykładach z mechaniki lotu. Do wyznaczania osiągów samolotu należy użyć metod
mechaniki lotu (Przewodnik po projektach z Mechaniki Lotu oraz opis projektu
Charakterystyki aerodynamiczne i osiągi samolotu).
1. Maksymalna doskonałość
Biegunowa analityczna samolotu ma postać:
C x = C x0
C 2z
+
π ⋅ A⋅ e
(1)
Gdzie:
A – wydłużenie płata
0,01 ≤ C x 0 ≤ 0,06
e ≈ 0,8
Doskonałość aerodynamiczna samolotu to stosunek siły nośnej do oporu, można ją więc
zapisać jako:
Cz
= Cz ⋅
Cx
1
C x0 +
C 2z
π ⋅ A⋅ e
(2)
Aby obliczyć dla jakiego Cz doskonałość jest maksymalna należy równanie (2)
zróżniczkować:
Cz
Cx
=
dC z
d
1
C x0 +
2
z
C
π ⋅ A⋅ e
+ Cz
2 ⋅ Cz
−1
2
π ⋅ A⋅ e 
C 2z 
 C x 0 +

π ⋅ A ⋅ e 

(3)
i pochodną przyrównać do zera:
1
0=
C x0 +
2
z
C
π ⋅ A⋅ e
+ Cz
2 ⋅ Cz
−1
2
π ⋅ A⋅ e 
C 2z 
 C x0 +



π
⋅
A
⋅
e


Cezary Galiński, Tomasz Grabowski - Materiały pomocnicze: Wyprowadzenie wzorów
(4)
1/9
Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Samolotów i Śmigłowców

C 2z 

Pomnóżmy teraz obie strony równania (4) przez  C x 0 +

π
⋅
A
⋅
e


2
C 2z
2 ⋅ Cz
C 2z
− Cz
= C x0 −
π ⋅ A⋅ e
π ⋅ A⋅ e
π ⋅ A⋅ e
0 = C x0 +
(5)
Z równania (5) możemy obliczyć Cz maksymalnej doskonałości:
Cz =
π ⋅ A ⋅ e ⋅ C x0
(6)
i odpowiadającą jej prędkość
V=
2W
ρS
1
(7)
π ⋅ A ⋅ e ⋅ C x0
Maksymalna doskonałość będzie więc miała wartość:
π ⋅ A ⋅ e ⋅ C x0
π ⋅ A ⋅ e ⋅ C x0
 Cz 


=
=
=
2
π
⋅
A
⋅
e
⋅
C
C
C
x
0
 x  max C +
z
C x0 +
x0
π ⋅ A⋅ e
π ⋅ A⋅ e
π ⋅ A ⋅ e ⋅ C x0
2 ⋅ C x0
=
1 π ⋅ A⋅ e
2
C x0
(8)
Znając maksymalną doskonałość samolotu można na tej podstawie obliczyć CX0.
2. Wznoszenie
Prędkość wznoszenia określona jest wzorem:
dH
= V sin γ =
dt
Ps
V dV
1+
g dH
(9)
Gdzie: Ps – nadmiar mocy
Ps = V
( T − D)
W
(10)
Dla dV/dH=0
sin γ =
T− D
= G
W
(11)
Gdzie: G – gradient wznoszenia
W = mg - ciężar
Cezary Galiński, Tomasz Grabowski - Materiały pomocnicze: Wyprowadzenie wzorów
2/9
Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Samolotów i Śmigłowców
D
T
=
−G
W W
(12)
D jest równe iloczynowi współczynnika oporu określonego biegunową analityczną (1),
powierzchni i ciśnienia dynamicznego. Iloraz D/W można więc przedstawić jako:
C 2z  q ⋅ S 
D q⋅ S
1
W2
 C x0 +
 =

=
C
+
x0
W
W 
π ⋅ A ⋅ e 
W 
π ⋅ A ⋅ e S 2q 2

 =

1 
W 2 1  qC x 0 W 1
 qSC x 0 + 2
 =
=
+
W
S π Aeq  W / S S qπ Ae
(13)
Wstawiając wynik przekształceń (13) do równania (12) otrzymamy:
qC x 0 W 1
T
+
=
− G
W / S S qπ Ae W
(14)
Pomnóżmy teraz obie strony przez W/S
2
qC x 0
1
 W
 T
 W
+ 
− 
− G
= 0

 S  qπ Ae  W
 S
(15)
Jak widać jest to równanie kwadratowe ze względu na W/S, którego ∆ równa jest:
2
C
 T

∆ = 
− G  − 4 x0
π Ae
 W

(16)
A rozwiązania mają postać:
W
=
S
 T

− G ±

W

2
C
 T

− G  − 4 x0

π Ae
 W

2
qπ Ae
(17)
Aby rozwiązania te miały wartości rzeczywiste, wyrażenie pod pierwiastkiem musi być
dodatnie. Stąd też otrzymujemy warunek na T/W:
C x0
T
≥ G+ 2
W
π Ae
Cezary Galiński, Tomasz Grabowski - Materiały pomocnicze: Wyprowadzenie wzorów
(18)
3/9
Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Samolotów i Śmigłowców
4. Zasięg –samoloty śmigłowe
Z równania Breguet’a wiemy że zasięg samolotu śmigłowego równy jest:
R=
C
η
⋅ z ⋅ ln( Wn / Wn + 1 )
C ⋅ g Cx
(19)
Maksymalny zasięg uzyskamy dla Cz maksymalnej doskonałości:
Cz =
π ⋅ A ⋅ e ⋅ C x0
(20)
Pamiętając, że
W = qSC z
(21)
Otrzymamy:
W
= q π ⋅ A ⋅ e ⋅ C x0
S
(22)
5. Zasięg –samoloty odrzutowe
Z równania Breguet’a wiemy że zasięg samolotu odrzutowego równy jest:
R=
V Cz
⋅
⋅ ln( Wn / Wn + 1 )
C ⋅ g Cx
(23)
Maksymalny zasięg uzyskamy gdy VCL/CD osiągnie wartość maksymalną, przy czym V
2W
możemy zastąpić przez V =
i otrzymamy:
ρ SC z
VC z C z
=
Cx
Cx
2W
=
ρ SC z
Cz
C x0 +
2
z
C
π Ae
2W
ρS
Wyrażenie to możemy teraz zróżniczkować po CL i przyrównać do zera:


VC z


∂


Cx
2C z
2W
1
1
−1


= 0=
+
C
z
2
2
∂ Cz
ρ S  2 Cz
π Ae 
C 2z


C
z
C x0 +
 C x0 +
 



π Ae
π Ae  


Cezary Galiński, Tomasz Grabowski - Materiały pomocnicze: Wyprowadzenie wzorów
(24)
(25)
4/9
Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Samolotów i Śmigłowców
A następnie uprościć


 1
2C z
2W
1
−1
0=
+ Cz
2 
ρS
π Ae 
Cz  2 Cz
C 2z 
 C x 0 +

C x0 +
π Ae 
π Ae 

2C z
1
−1
=
+ Cz
π Ae 
2 Cz
C 2z 
 C x0 +



π
Ae





 =



(26)
Cz
Pomnóżmy teraz obie strony przez
Cx0 +
C 2z
π Ae
C 2z  2C 2z C x 0 3 C 2z
1
−
0 =  C x 0 +
=
−
2
π Ae  π Ae
2
2 π Ae
(27)
I przekształćmy w celu obliczenia Cz
Cx 0 3 C2z
=
2
2 π Ae
Cz =
C x 0 π Ae
3
(28)
Pamiętając, że
W
= qC z
S
Otrzymamy, że największy zasięg samolotu odrzutowego uzyskamy gdy:
W
Cz 0 π Ae
= q
S
3
Cezary Galiński, Tomasz Grabowski - Materiały pomocnicze: Wyprowadzenie wzorów
(29)
5/9
Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Samolotów i Śmigłowców
6. Zakręt dowolny

ψ
Z warunków równowagi w zakręcie
wynika, że:
 W = L cos ϕ

 mV 2
= L sin ϕ

 r
(30)

L
ϕ
Przechylenie samolotu wiąże się ze
wzrostem współczynnika obciążenia:
cos ϕ =
W 1
=
L n
(31)
r
Pamiętając, że:
cos 2 ϕ + sin 2 ϕ = 1
(32)
Możemy zapisać:
2
 1
  + sin 2 ϕ = 1
 n
sin ϕ =
1−
1
n2
(33)
Wstawiając (33) do drugiego równania z układu (30) otrzymamy promień zakrętu:
mV 2
W V2
V2
V2
r=
=
=
=
L sin ϕ
L g sin ϕ ng sin ϕ g n 2 − 1
(34)
Prędkość kątowa wynika ze związku pomiędzy prędkością kątową i liniową w ruchu po łuku
V = ψ r
(35)
Wstawiamy (34) do (35), upraszczamy i otrzymujemy
ψ =
V Vg n 2 − 1 g n 2 − 1
=
=
r
V
V
(36)
A przekształcając na n:
Cezary Galiński, Tomasz Grabowski - Materiały pomocnicze: Wyprowadzenie wzorów
6/9
Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Samolotów i Śmigłowców
2
 Vψ 

 + 1
 g 
n=
(37)
Pamiętamy, że współczynnik obciążenia jest zdefiniowany jako:
n=
L qC z max
=
W
W/S
(38)
Wstawiając więc (37) do (38) otrzymamy obciążenie powierzchni pozwalające na
wykonywanie zakrętów przy założonej prędkości kątowej:
W
=
S
qCz max
2
 ψ V 

 + 1
 g 
(39)
7. Zakręt prawidłowy
Zakręt prawidłowy, to taki w którym pułap lotu samolotu nie ulega zmianie. Układ (30)
gwarantował brak przyspieszeń w kierunku pionowym. Nie pozwalał jednak wnioskować o
ustalonej prędkości opadania/wznoszenia. Będzie ona równa zeru, jeśli w zakręcie spełniony
będzie warunek:
T= D
(40)
Wstawiając biegunową równowagi (1) otrzymamy:
T = qS(Cx 0 +
C2z
)
π Ae
(41)
Z kolei podzieliwszy równanie (41) przez W mamy:
T qS 
C 2z 
 C x 0 +

=
W W
π Ae 
(42)
pamiętając że
n=
Cz =
L Cz qS
=
W
W
nW
qS
(43)
(44)
Możemy wyeliminować Cz z równania (42):
Cezary Galiński, Tomasz Grabowski - Materiały pomocnicze: Wyprowadzenie wzorów
7/9
Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Samolotów i Śmigłowców
T qC x 0 W n 2
=
+
W W / S S qπ Ae
(45)
Pomnóżmy je teraz przez W/S
2
2
T w
 W n
−
+ qCx 0 = 0


 S  qπ Ae W s
(46)
Otrzymaliśmy równanie kwadratowe ze względu na W/S, dla którego
2
4n 2qCx 0
 T
∆ = 
 −
qπ Ae
 W
(47)
A rozwiązania mają postać:
2
4n 2Cx 0
 T

 −
π Ae
 W
2
2n
qπ Ae
T
±
W
W
=
S
(48)
Wyrażenie pod pierwiastkiem musi być dodatnie skąd otrzymujemy warunek na T/W
T
Cx 0
≥ 2n
W
π Ae
(49)
Z równania (45) możemy też wyliczyć maksymalny współczynnik obciążenia w zakręcie
prawidłowym
qπ Ae   T 
qCx 0 
 

−

W / S   W  max W / S 
n max =
(50)
A ponieważ:
ψ =
g n2 − 1
V
(51)
Więc maksymalna prędkość kątowa w zakręcie prawidłowym wyniesie:
g
ψ max =
qπ Ae   T 
qC x 0 
 
−1
−

W / S   W  max W / S 
V
Cezary Galiński, Tomasz Grabowski - Materiały pomocnicze: Wyprowadzenie wzorów
(52)
8/9
Wydział Mechaniczny Energetyki i Lotnictwa Politechniki Warszawskiej - Zakład Samolotów i Śmigłowców
8. Prędkość maksymalna
W warunkach równowagi przy prędkości maksymalnej (większej lub równej zakładanej) w
locie poziomym spełnione są równania:
ρ V2
SC x
2
ρ V2
Pz =
SC z
2
Px ≤ T
Pz = mg
Px =
(53)
(54)
(55)
(56)
Zakładając wyposażenie samolotu w śmigło o zmiennym skoku można przyjąć że sprawność
śmigła jest bliska maksymalnej i nie mniejsza niż 80%. Ponadto można przyjąć biegunową
analityczną w postaci (1)
Wstawiając (53) i (1) do (55) otrzymujemy:
ρ V2
2

C 2z 

 ≤ T
S C x 0 +

π
Λ
e


(57)
Z kolei wstawiając (56) do (54) otrzymujemy:
Cz =
2mg
ρ V 2S
(58)
Można teraz wstawić (58) do (57)
ρ V2
2

4m 2 g 2
S C x 0 +
π Λ eρ 2 S 2 V 4


 ≤ T

(59)
Dzieląc obie strony przez mg mamy:
ρ V2 
4m 2 g 2
S C x 0 +
2mg 
π Λ eρ 2 S 2 V 4
 T
 ≤
 mg
(60)
Wiedząc, że mg = W dostaniemy ostatecznie:
ρ V2 S 
4
W2 
T
 C x 0 +
 ≤
2
4
2 
2 W
π Λ eρ V S  W
Cezary Galiński, Tomasz Grabowski - Materiały pomocnicze: Wyprowadzenie wzorów
(61)
9/9