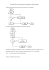Rekurencja

Rekurencja
Przygotowała:
Agnieszka Reiter
Definicja
• Charakterystyczną cechą funkcji (procedury)
rekurencyjnej jest to, że wywołuje ona samą
siebie. Drugą cechą rekursji jest jej dziedzina,
którą mogą być tylko liczby naturalne.
• Rekurencja jest sposobem programowania, w
którym stosuje się procedury wywołujące same
siebie. Ilość tych wywołań nie ma znaczenia,
fakt wywołania jest podstawą do określenia
algorytmu jako rekurencyjnego.
Po co nam jest rekurencja?
Przede wszystkim dzięki niej łatwo jest wykonać
wiele zadań, w których potrzeba jest wyników
cząstkowych do obliczenia całości.
Sztandarowym przykładem w zagadnieniu
rekurencji jest liczenie silni (n!), lub nieco
bardziej zaawansowany przykład liczenia n-tej
wartości w ciągu Fibonacciego.
Dla przypomnienia, ciąg Fibonacciego jest
ciągiem, w którym każda następna wartość jest
równa sumie dwóch poprzednich.
Algorytm silnia
ALGORYTM SILNI W J. PASCAL
Function silnia(n:byte):word;
Begin
If n<1 then silnia:=1
else silnia:=silnia(n-1)*n;
End;
Algorytm silni
Często przytaczanym przykładem jest
definicja funkcji obliczającej wartość silni
long int SILNIA(int n)
{
if(n<1) return 1;
else return n * SILNIA(n-1);
}
Analiza
Odwołanie się do funkcji wewnątrz tej samej
funkcji następuje z parametrem o 1 mniejszym,
niż oryginalnie podano.
Dlatego kolejna wersja funkcji będzie liczyła
wartość silni już tylko dla np. 5, podczas gdy
początkowe wywołanie było dla 6.
Kolejne poziomy wywołań funkcji SILNIA będą
liczyły silnię dla coraz mniejszych wartości, aż
do 0, a wtedy zwrócone zostanie 1.
Potem, zwracane są kolejne wartości podczas
wychodzenia z kolejnych poziomów wywołań,
i wtedy właśnie będzie obliczana rzeczywista
wartość (będą mnożone przez siebie kolejne
liczby).
Przykład - silnia(6)
Uwaga
Cechą charakterystyczną jest to, że
funkcja wchodzi w kolejny poziom,
aby obliczyć iloczyn podanego jej
parametru oraz wartość (parametr-1).
Dopiero w momencie powrotu
z wywołań obliczane są rzeczywiste
iloczyny, i wtedy też przeliczana jest
wartość silni.
Ciąg fibonacciego
• Liczby naturalne tworzące ciąg o takiej
własności, że kolejny wyraz (z wyjątkiem dwóch
pierwszych) jest sumą dwóch poprzednich
nazywa się liczbami Fibonacciego i pojawiają się
w tak wielu sytuacjach, że wydaje się to
niemożliwe.
• Podstawowy ciąg liczb Fibonacciego to: 1, 1, 2,
3, 5, 8, ... Każda liczba w ciągu jest sumą dwóch
poprzednich (poza pierwszą i drugą). Mamy
więc do czynienia z ciągiem rekurencyjnym.
Występowanie
• Ciąg Fibonacciego można odnaleźć
w wielu aspektach przyrody, ciąg taki opisuje
np. liczbę pędów rośliny jednostajnie
przyrastającej w latach.
• W słoneczniku możemy zaobserwować dwa
układy linii spiralnych, wychodzących ze środka.
• Takie same spirale można zaobserwować na
wielu innych roślinach ( np. kalafior, ananas).
• Liczby spiral występujących w tych roślinach
są kolejnymi liczbami Fibonacciego.
Ciąg fibonacciego w j. Pascal
Function fibonacci(n:byte):word;
Begin
If ((n=1) or (n=2)) then fibonacci:=1
Else
fibonacci := fibonacci(n-1)+fibonacci(n-2);
End;
Ciąg Fibonacciego C++
#include <iostream>
using namespace std;
int Fibonacci(int n)
{
if (n==1 || n==2)
return 1;
else
return Fibonacci(n-1) + Fibonacci(n-2);
}
int main()
{
int n;
cout << "Podaj n= ";
cin >> n;
cout << n << " wyraz ciagu Fibonacciego to: " << Fibonacci(n)
<<endl;
system("pause>null");
return 0;
}
Wieże HANOI
Wieże Hanoi – problem polegający na odbudowaniu,
z zachowaniem kształtu, wieży z krążków o różnych
średnicach (popularna dziecięca zabawka), przy czym
podczas przekładania wolno się posługiwać buforem
(reprezentowanym w tym przypadku przez dodatkowy
słupek), jednak przy ogólnym założeniu, że nie wolno
kłaść krążka o większej średnicy na mniejszy ani
przekładać kilku krążków jednocześnie. Jest to przykład
zadania, którego złożoność obliczeniowa wzrasta
niezwykle szybko w miarę zwiększania parametru
wejściowego, tj. liczby elementów wieży.
Rozwiązania
Dla 2 krążków:
Dla 3 krążków:
rozwiązanie dla 3 krążków składa się z 7 ruchów:
kolejne etapy to:
• przenieś krążek o najmniejszej średnicy na palik docelowy,
• krążek o średnicy większej przenieś na palik pomocniczy,
• krążek najmniejszy przenieś na palik pomocniczy,
• następnie krążek największy przenieś na palik docelowy a najmniejszy
na źródłowy,
• na największym połóż średni i potem najmniejszy,
• koniec
Wieża Hanoi
• Ułóż stos na trzecim patyku przestrzegając następujących
reguł:
- przesuwaj jeden krążek z wierzchu stosu,
- nie kładź większego krążka na mniejszym.
bufora
Od lewej: słupek A
z całą wieżą,
pusty słupek B
pełniący rolę
i pusty słupek
docelowy C
Wieża Hanoi
Wynik końcowy
Ruchy pośrednie
Algorytm
Rozwiązanie rekurencyjne:
1. Zidentyfikuj największy krążek na nie swoim
miejscu (=krążek N)
2. If daje się go przenieść na docelowy słupek
Then przenieś
Else
3. Podzadanie: ustaw (N−1)-krążkową
wieżę na nie-docelowym słupku.
4. Skocz do punktu 1. ...
Rozwiązanie rekurencyjne
Algorytm rekurencyjny składa się z następujących
kroków:
• przenieś (rekurencyjnie) n-1 krążków ze słupka
A na słupek B posługując się słupkiem C,
• przenieś jeden krążek ze słupka A na słupek C,
• przenieś (rekurencyjnie) n-1 krążków ze słupka
B na słupek C posługując się słupkiem A
Implementacja w C++
#include <iostream>
using namespace std;
void hanoi(int n, char A, char B, char C)
{ // przekłada n krążków z A korzystając z B na C
if (n > 0) {
hanoi(n-1, A, C, B);
cout << A << " -> " << C << endl;
hanoi(n-1, B, A, C); } }
int main(int argc, char *argv[])
{
hanoi(3, 'A', 'B', 'C');
return 0;
}