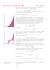1. Liczby rzeczywiste

Transkrypt

3
Spis treści
OD AUTORÓW ................................................................................ 4
1. LICZBY RZECZYWISTE ............................................................................................. 5
1.1. DZIAŁANIA ARYTMETYCZNE....................................................................................... 5
1.2. KOLEJNOŚĆ DZIAŁAŃ MATEMATYCZNYCH ................................................................. 8
1.3. LICZBY NATURALNE, CAŁKOWITE, WYMIERNE I NIEWYMIERNE .................................. 8
1.4. DZIAŁANIA NA UŁAMKACH ......................................................................................... 9
1.5. UŁAMKI DZIESIĘTNE ................................................................................................. 12
1.6. PROCENTY ................................................................................................................ 13
1.7. POTĘGOWANIE I DZIAŁANIA NA POTĘGACH............................................................... 14
1.8. WZORY SKRÓCONEGO MNOŻENIA ............................................................................. 15
1.9. PIERWIASTKOWANIE ................................................................................................. 16
1.10. WARTOŚĆ BEZWZGLĘDNA (MODUŁ) LICZBY ........................................................... 18
1.11. PIERWIASTEK NIEPARZYSTEGO STOPNIA Z LICZBY UJEMNEJ ................................... 18
1.12. POTĘGA O WYKŁADNIKU RZECZYWISTYM .............................................................. 19
1.13. DZIAŁANIA NA WYRAŻENIACH NIEWYMIERNYCH ................................................... 20
1.14. RELACJE ................................................................................................................. 21
1.15. RÓWNANIA I NIERÓWNOŚCI. PRZEDZIAŁY .............................................................. 22
2. ZADANIA RÓŻNE ....................................................................................................... 25
2.1. PRZEKSZTAŁCANIE WYRAŻEŃ WYMIERNYCH............................................................ 25
2.2. PRZEKSZTAŁCANIE WYRAŻEŃ NIEWYMIERNYCH ...................................................... 27
2.3. ROZWIĄZYWANIE RÓWNAŃ I NIERÓWNOŚCI LINIOWYCH .......................................... 31
2.4. ROZWIĄZYWANIE RÓWNAŃ I NIERÓWNOŚCI KWADRATOWYCH ................................ 39
3. ROZWIĄZANIA ZADAŃ ............................................................................................ 49
4. LITERATURA .............................................................................................................. 72
4
Od Autorów
U podstaw decyzji o wydaniu serii zeszytów pod wspólnym tytułem „Ćwiczenia z matematyki” są nasze wieloletnie doświadczenia nauczycieli akademickich w zakresie nauczania przedmiotów ilościowych (matematyka, statystyka matematyczna, doświadczalnictwo,
ekonometria) jak i informatycznych (arkusze kalkulacyjne, relacyjne bazy danych).
Od szeregu lat obserwujemy narastające problemy znacznej grupy studiujących ze
zrozumieniem tych przedmiotów, przy czym jest to szczególnie groźne w przypadku osób
studiujących w trybie zaocznym.
Seria „Ćwiczenia z matematyki” została pomyślana z jednej strony jako materiał
ułatwiający przypomnienie programu matematyki z zakresu szkoły średniej. Z drugiej
strony materiał zawarty w tej serii jest już pewnym przygotowaniem pod nauczanie takich
przedmiotów jak właśnie statystyka, ekonometria, arkusze kalkulacyjne, bazy danych czy
badania operacyjne.
Seria „Ćwiczenia z matematyki” powinna być traktowana raczej jako literatura uzupełniająca klasyczną literaturę przedmiotu (podawaną przez prowadzących poszczególne
przedmioty) niż jako jedyny i wystarczający do zrozumienia matematyki skrypt. Mamy
jednak nadzieję, że przedstawiony materiał z szeregiem szczegółowych przykładów ułatwi
zrozumienie tych wybranych działów matematyki.
W serii „Ćwiczenia z matematyki” wstępnie zaplanowano ukazanie się następujących
pozycji:
•
Zeszyt 1. Funkcje i ciągi liczbowe
•
Zeszyt 2. Granice ciągów i funkcji. Pochodna i jej zastosowanie
•
Zeszyt 3. Całki i ich zastosowania
•
Zeszyt 4. Macierze i rozwiązywanie układów równań liniowych
•
Zeszyt 5. Równania różniczkowe i ich zastosowania.
Praktyka trochę zmodyfikowała te wstępne plany, zeszyty 1-4, których autorem jest dr
Janusz Górczyński, ukazały się w latach 2000-2001, w roku 2002 pojawił się nowy
Zeszyt 6 napisany przez dr Andrzeja Zielińskiego z zamysłem, aby umożliwić studentom
samoocenę posiadanej wiedzy matematycznej. Wydanie Zeszytu 5 odsuwa się na trochę
dalszy plan, ale nie rezygnujemy z jego wydania.
Ten zeszyt pojawił się z potrzeby chwili i jako pewne uzupełnienie wcześniejszych
zeszytów. Po prostu jest bardzo duża grupa kandydatów i studentów, którzy muszą przypomnieć sobie rzeczy elementarne.
Janusz Górczyński
Andrzej Zieliński
5
1. Liczby rzeczywiste
Pod pojęciem „zbiór liczb rzeczywistych” rozumiemy wszystkie możliwe liczby, zbiór
ten będziemy oznaczać literą R, a jego elementy małymi literami alfabetu. Fakt, że jakaś
liczba, powiedzmy x, należy do zbioru liczb rzeczywistych zapiszemy następująco:
x∈R .
Zbiór R jest zbiorem nieskończonym, co oznacza, że zawiera nieskończenie wiele
elementów. Inaczej mówiąc zbiór R nie zawiera ani elementu najmniejszego, ani elementu
największego. Umownie mówimy, że zbiór R rozciąga się od minus do plus
nieskończoności. Te dwa umowne „krańce” będziemy oznaczać odpowiednio jako −∞
oraz +∞ .
Graficznie zbiór liczb rzeczywistych można przedstawić na osi liczbowej, na której
zaznaczamy kierunek zwiększania się liczb oraz jeden lub więcej punktów charakterystycznych. Na pokazanej niżej osi liczbowej zaznaczone zostało zero jako punkt
charakterystyczny (punkt odniesienia); liczba zero dzieli zbiór liczb rzeczywistych na trzy
podzbiory: zbiór liczb ujemnych ( R − ), liczbę zero oraz zbiór liczb dodatnich ( R + ).
1
0
1.1. Działania arytmetyczne
W zbiorze R zdefiniowane są cztery działania:
x+ y = {
z
dodawanie
1
424
3
skladniki
odejmowanie
odjemna
mnożenie
odjemnik
różnica
x⋅ y = {
z
123
czynniki
dzielenie
suma
x − {
y = {
z
{
iloczyn
x : {
y ={
z
{
dzielna dzielnik
gdzie y ≠ 0 .
iloraz
Jeżeli nie prowadzi to do nieporozumień, możemy w zapisie mnożenia opuścić znak
mnożenia (symbol kropki), np. możemy napisać 2 x zamiast 2 ⋅ x , czy xy zamiast x ⋅ y .
Ale zapis x 2 nie musi oznaczać mnożenia, lepiej więc pisać x ⋅ 2 , a już na pewno 23 nie
oznacza 2 ⋅ 3 !
6
Odejmowanie jest działaniem odwrotnym do dodawania:
x− y = z ⇔ z+ y = x,
gdzie symbol ⇔ oznacza: „wtedy i tylko wtedy, gdy...”. Inaczej mówiąc z warunku
x − y = z wynika warunek z + y = x i odwrotnie.
Liczba zero jest wynikiem odejmowania w sytuacji, gdy odjemna i odjemnik są sobie
równe: x − x .
Dla każdego x ∈ R zachodzi:
x ⋅0 = 0⋅ x = 0 .
Dla x, y ∈ R zachodzą następujące równoważności:
x = y ⇔ x− y =0
x < y ⇔ x− y < 0
x > y ⇔ x− y >0
Liczbę x < 0 nazywamy liczbą ujemną, a x > 0 liczbą dodatnią. Różnicę 0 − x
oznaczamy symbolem − x i nazywamy liczbą przeciwną do x . Suma liczby x i liczby
przeciwnej do niej, czyli − x , jest równa zero:
x + (− x) = x − x = 0 .
Przy oznaczaniu liczby dodatniej x można użyć zarówno symbolu x jak i + x
(poprzedzić ją symbolem plus, np. można pisać zarówno 5 jak i +5 ). Liczba ujemna musi
być poprzedzona symbolem minus.
Obowiązują następujące prawa (tzw. prawa znaków):
+ (+ x) = + x
− (+ x) = − x
+ (− x) = − x
− (− x) = + x .
Dzielenie jest działaniem odwrotnym do mnożenia:
x: y = z ⇔ y⋅z = x
Dzielenie może być zapisane jako x : y lub
x
y
dla y ≠ 0
. Wyrażenie
x
y
nazywamy ułamkiem.
Dzielną x nazywamy wtedy licznikiem, a dzielnik y mianownikiem.
Liczbę
1
x
( x ≠ 0) nazywamy liczbą odwrotną do liczby x. Iloczyn liczby x przez jej
odwrotność jest równy jeden:
x ⋅ 1x = 1 .
7
Wykorzystując pojęcie liczby odwrotnej do danej liczby można przedstawić dzielenie
jako mnożenie przez liczbę odwrotną. Przykładowo:
6:2 =
6
2
= 6 ⋅ 12 .
Wynik każdego działania arytmetycznego musi być określony i to jednoznacznie,
dlatego też dzielenie przez zero nie jest możliwe! Rozpatrzmy przykładowe sytuacje:
a) 0 : 5 =
0
5
b) 5 : 0 =
5
0
c) 0 : 0 =
0
0
= 0 , ponieważ 5 ⋅ 0 = 0 ,
nie istnieje, bo gdyby
5
0
= z , to musiałaby zachodzić równość z ⋅ 0 = 5 ,
nie istnieje, ponieważ wynik nie jest określony jednoznacznie, tzn. każda
liczba rzeczywista może być wynikiem:
0
0
= z ⇔ z⋅0 = 0 .
Liczbę zero nazywamy elementem obojętnym (tzw. modułem) dla dodawania,
ponieważ:
x+0 = 0+ x = x .
Liczbę jeden nazywamy elementem obojętnym (tzw. modułem) dla mnożenia,
ponieważ:
x ⋅1 = 1 ⋅ x = x .
Działania arytmetyczne podlegają następującym prawom:
Prawo łączności dodawania
( x + y) + z = x + ( y + z)
Prawo przemienności dodawania
x+ y = y+x
Prawo łączności mnożenia
( x ⋅ y) ⋅ z = x ⋅ ( y ⋅ z)
Prawo przemienności mnożenia
x⋅ y = y⋅x
Prawo rozdzielności mnożenia względem dodawania
( x + y) ⋅ z = x ⋅ z + y ⋅ z
8
Prawdziwe są następujące wzory określające znak mnożenia (także dzielenia):
(+ x) ⋅ (+ y ) = + x ⋅ y
(− x) ⋅ (+ y ) = − x ⋅ y
(+ x ) ⋅ ( − y ) = − x ⋅ y
.
(− x ) ⋅ (− y ) = + x ⋅ y
1.2. Kolejność działań matematycznych
Kolejność działań matematycznych określona jest następującymi dwoma regułami:
•
Jeżeli w wyrażeniu występują nawiasy, to najpierw wykonywane są działania
wewnątrz nawiasów,
•
Jeżeli nie ma nawiasów, to najpierw wykonujemy mnożenia i dzielenia, a następnie dodawania i odejmowania, przy czym działania wykonywane są
w kolejności ich wykonywania od lewej do prawej strony wyrażenia.
Przykład 1. Mamy obliczyć wartość wyrażenia (kursywą komentarz):
4 − 6 : 3 − 2 + 20 : 5 ⋅ 2 =
Wykonujemy dzielenia 6:3 i 20:5
= 4 − 2 − 2 + 4⋅2 =
Wykonujemy mnożenie 4·2
= 4−2−2+8 =
Kolejno odejmujemy i dodajemy
= 2−2+8 =
= 0+8 = 8
Przykład 2. Obliczmy wartość wyrażenia (kursywą komentarz):
{4 ⋅ 7 − [(4 ⋅ 3 + 8 : 4) − (2 ⋅ 6 − 10)] ⋅ 5} + 3 ⋅ (4 ⋅ 7 − 26) =
Wykonujemy najpierw działania w nawiasach otrzymując:
{4 ⋅ 7 − [(12 + 2) − (12 − 10)] ⋅ 5} + 3 ⋅ ( 28 − 26) = {4 ⋅ 7 − [14 − 2] ⋅ 5} + 3 ⋅ (2) =
= {28 − 12 ⋅ 5} + 6 = {28 − 60} + 6 = −32 + 6 = −26
1.3. Liczby naturalne, całkowite, wymierne
i niewymierne
Zbiór N liczb naturalnych tworzą liczby { 1, 2, 3, ....} . Zbiór liczb
naturalnych jest
ograniczony z dołu przez liczbę 1, inaczej mówiąc w zbiorze tym istnieje element
najmniejszy. Zbiór N jest nieograniczony od góry, czyli nie istnieje element największy.
Wynik dodawania czy mnożenia dwóch liczb naturalnych jest zawsze liczbą naturalną.
Odejmowanie dwóch liczb naturalnych nie zawsze daje w wyniku liczbę naturalną (np.
2 − 5 ), natomiast jest ono wykonalne w zbiorze liczb całkowitych.
9
Zbiór C liczb całkowitych tworzą liczby {... − 3, − 2, − 1, 0, 1, 2, 3, ....} . Zbiór liczb
całkowitych jest nieograniczony zarówno z dołu (nie istnieje element najmniejszy), jak i od
góry (nie istnieje element największy).
Dzielenie dwóch liczb całkowitych nie zawsze daje w wyniku liczbę całkowitą. Niech
m, n ∈ C oraz n ≠ 0 . Liczba m jest podzielna przez n wtedy i tylko wtedy, gdy iloraz
m : n jest liczbą całkowitą. Liczbę n nazywamy wtedy podzielnikiem m.
Liczby naturalne podzielne przez dwa nazywamy liczbami parzystymi, a niepodzielne
przez dwa liczbami nieparzystymi.
Taką liczbę naturalną różną od jeden, której podzielnikiem jest jeden i ona sama
nazywamy liczbą pierwszą. Przykładem liczb pierwszych są:
2, 3, 5, 7, 11, 13, 17, 19, 23, ....
Liczby pierwsze znajdują bardzo ważne zastosowanie w nowoczesnych technologiach
szyfrowania, a bez nich trudno byłoby mówić o np. komercyjnym wykorzystywaniu
Internetu.
Niech a, b ∈ C oraz b ≠ 0 . Liczbę postaci
a
b
nazywamy liczbą wymierną. Przykładowe liczby wymierne:
1 3 9
−4 8
,
,
,
, =8.
2 2 4
7 1
a
nazywamy ułamkiem zwykłym. Dla a b ułamek niewłaściwy.
Dla a, b ∈ N oraz b ≠ 0 iloraz
Pozostałe liczby rzeczywiste nazywamy liczbami niewymiernymi. Takimi liczbami są
np. 2 (długość przekątnej kwadratu o boku 1), π (stosunek długości okręgu do jego
promienia) czy e (podstawa logarytmu naturalnego).
1.4. Działania na ułamkach
Wartość ułamka nie zmieni swojej wartości, jeżeli jego licznik i mianownik pomnożymy lub podzielimy przez tę samą liczbę różną od zera. W przypadku mnożenia mówimy
o rozszerzaniu ułamka, a przy dzieleniu o skracaniu.
a a ⋅c
=
b b⋅c
rozszerzanie, c ≠ 0 ,
10
a⋅c a
=
b⋅c b
skracanie, c ≠ 0 .
Przy dodawaniu lub odejmowaniu ułamków musimy sprowadzić je do wspólnego
mianownika:
a c a ⋅d ± b⋅c
.
± =
b d
b⋅d
Wspólny mianownik musi być tak dobrany, by poszczególne mianowniki były jego
czynnikami. Nie oznacza to, że zawsze trzeba wziąć jako wspólny mianownik iloczyn
wszystkich mianowników.
Przykład 3. Obliczmy wartość wyrażenia
5
3 13
+
−
.
12 20 24
Bierzemy najpierw iloczyn m1 = 3 ⋅ 4 = 12 . W iloczynie 4 ⋅ 5 = 20 powtarza się czynnik
4, natomiast „nowym” czynnikiem w stosunku do iloczynu m1 jest 5. Bierzemy więc
iloczyn m2 = 3 ⋅ 4 ⋅ 5 . W iloczynie 2 ⋅ 3 ⋅ 4 = 24 powtarza się iloczyn 3 ⋅ 4 , a nowym
czynnikiem w stosunku do m2 jest 2. Bierzemy więc jako wspólny mianownik iloczyn
m3 = 2 ⋅ 3 ⋅ 4 ⋅ 5 = 120 .
5
3 13 5 ⋅ 10
3 ⋅ 6 13 ⋅ 5 50 + 18 − 65
3
1
+
−
=
+
−
=
=
=
.
12 20 24 12 ⋅ 10 20 ⋅ 6 24 ⋅ 5
120
120 40
Oczywiście nie byłoby błędem wzięcie jako wspólny mianownik iloczynu liczb
występujących w mianownikach poszczególnych ułamków, czyli 12 ⋅ 20 ⋅ 24 = 5760 , tylko
rachunki byłyby bardziej skomplikowane.
Przykład 4. Obliczmy wartość wyrażeń:
a)
5 7 1
5 5 ⋅ 4 7 ⋅ 3 1⋅ 2
5
20 + 21 + 2 + 5 48
+ + +
=
+
+
+
=
=
=2
6 8 12 24 6 ⋅ 4 8 ⋅ 3 12 ⋅ 2 24
24
24
b)
1 23 9
1 46 9 56 1 − 46 + 9 + 56 20
− + + 14 = −
+ +
=
=
=5
4 2 4
4 4 4 4
4
4
c) 21 +
12 22 5
21
12 + 5 22 + 21
+
+ +3+
= 24 +
+
= 24 + 1 + 1 = 26 .
17 43 17
43
17
43
Przy mnożeniu ułamków mnożymy liczniki i mianowniki:
a c a ⋅c
⋅ =
.
b d b⋅d
11
Przy dzieleniu ułamków pierwszy z nich mnożymy przez odwrotność drugiego:
a c
: =
b d
a
b
c
d
=
a d a⋅d
⋅ =
.
b c b⋅c
Z powyższych wzorów wynika, że
a
a⋅c
a
a c a⋅c a⋅c
⋅c =
, bo ⋅ c = ⋅ =
=
.
b
b
b
b 1 b ⋅1
b
Przypomnijmy także, że każda równość może być czytana również od strony prawej do
a⋅c
a
c
lewej, czyli np. od postaci
można przejść do postaci ⋅ c jak i do postaci a ⋅ :
b
b
b
a⋅c a
c
= ⋅c = a⋅ .
b
b
b
a±b a b
= ± .
c
c c
c
c c
12
12
= ± . Wystarczy porównać np.
Nie jest natomiast prawdą, że
=
=2
a±b a b
2+4 6
12 12
z
+
= 6+3= 9.
2
4
Z prawa rozdzielności mnożenia względem dodawania wynika wzór
Dla ułamków prawdziwe są następujące wzory:
−a
a
a
=− =
,
b
b −b
a + a −a
=
=
.
b +b −b
12
1.5. Ułamki dziesiętne
Każdą liczbę rzeczywistą można zapisać w postaci dziesiętnej. Zapis dziesiętny składa
się z części całkowitej i części ułamkowej rozdzielonych przecinkiem, np.
1,4142 = 1 +
4
1
4
2
14142
+
+
+
=
.
10 100 1000 10000 10000
Jeśli mianownik ułamka zwykłego jest podzielnikiem 10, 100, 1000 itd., to taki ułamek
można zamienić na ułamek dziesiętny mnożąc jego licznik i mianownik przez odpowiednią
liczbę, np.:
6
6⋅4
24
=
= 0,24 ,
=
25 25 ⋅ 4 100
1
1⋅ 8
8
=
= 0,008 ,
=
125 125 ⋅ 8 1000
78 78 ⋅ 2 156
=
=
= 15,6 .
5
5⋅2
10
W tych przypadkach mówimy, że dana liczba ma rozwinięcie dziesiętne skończone, tzn.
6
= 0,24 = 0,240 itd.
po przecinku występuje skończona liczba cyfr różnych od zera, np. 25
W pozostałych przypadkach (ale również w wyżej opisanych) zamianę ułamka zwykłego
na dziesiętny można wykonać stosując algorytm „dzielenia pod kreską”, który w nieco
zmodyfikowanej postaci przedstawia przykład 5.
Przykład 5. Mamy podać zapis dziesiętny ułamka
dzielenie
m:n
7:33
70:33
40:33
70:33
40:33
wynik całkowity k
(n mieści się k razy w m)
0
2
1
2
1
Wobec tego
7
33
reszta
m-k⋅n
7
4
7
4
7
7
:
33
reszta⋅10
(kolejne m)
70
40
70
40
70
ułamek dziesiętny
(kolejne przybliżenie)
0
0,2
0,21
0,212
0,2121
≈ 0,2121 . Równość jest przybliżona, ponieważ w nieskończoność
będzie się po przecinku pojawiał okres (21). Używając dokładnej równości napisalibyśmy
7
= 0, (21) .
33
13
Mówimy, że ułamek
7
33
ma rozwinięcie dziesiętne nieskończone okresowe. Każda
liczba wymierna ma rozwinięcie dziesiętne skończone albo okresowe nieskończone.
Natomiast rozwinięcie dziesiętne liczby niewymiernej jest zawsze nieskończone, przy
czym nie można wskazać ciągu cyfr (okresu), który by powtarzał się w nieskończoność.
Mnożenie (dzielenie) ułamka dziesiętnego przez 10, 100, 1000 itd. polega na
przesunięciu przecinka o 1, 2, 3, itd. miejsca w prawo (lewo).
Przykład 6. Mamy obliczyć a = 4 ⋅ 0,125 .
Obliczamy najpierw b = 1000 ⋅ a = 4 ⋅ 0,125 ⋅ 1000 = 4 ⋅ 125 = 500 . Żeby obliczyć a ,
trzeba teraz b podzielić przez 1000, tak więc a = 500 : 1000 = 0,5 , czyli 4 ⋅ 0,125 = 0,5 .
Przykład 7. Obliczmy wartość wyrażenia 0,15 : 0,3 .
Mamy
0,15 0,15 ⋅ 100 15
=
=
= 0,5 .
0,3
0,3 ⋅ 100 30
Przykład 8. Obliczmy wartość wyrażenia
(0,3 − 0,15) : 0,3
.
(1,88 + 2,12) ⋅ 0,125
(0,3 − 0,15) : 0,3
0,15 : 0,3 0,5
=
=
= 1.
(1,88 + 2,12) ⋅ 0,125 4 ⋅ 0,125 0,5
1.6. Procenty
Jeden procent pewnej liczby to
1
100
część tej liczby. Przykładowo:
1% liczby 25 to 0,25
1% liczby 12,34 to 0,1234
1% liczby 1345,5 to 13,455.
Z określenia procentu wynikają następujące związki:
p% liczby a jest równe
p⋅a
,
100
liczba, której p% wynosi b, jest równa
b ⋅100
.
p
14
Przykład 9. Obliczmy:
a) 4% liczby 62. Rozwiązanie:
4 ⋅ 62
= 2,48
100
b) 36% liczby 130. Rozwiązanie:
36 ⋅ 130
= 0,36 ⋅ 130 = 46,8
100
c) liczbę, której 15% wynosi 8. Rozwiązanie:
8 ⋅100 8 ⋅ 20
=
= 53, (3)
15
3
d) liczbę, której 70% wynosi 45. Rozwiązanie:
45 ⋅100 450
=
= 64, (285714)
70
7
Przykład 10. Jeden bok prostokąta skrócono o 50%, a drugi wydłużono o 50%. Jak
zmieni się pole prostokąta?
Początkowe boki prostokąta to x i y, a jego pole P = x ⋅ y . Pierwszy bok skrócono
o 50%, czyli jego długość jest równa 50% ⋅ x = 0,5 ⋅ x , a drugi powiększono o 50%, stąd
jego długość jest równa y + 50% y = 1,5 y . Tym samym pole tak zmienionego prostokąta
jest równe P' = (0,5 x) ⋅ (1,5 y ) = 0,75 xy . Jak widzimy, pole prostokąta zmniejszyło się
o 25%.
1.7. Potęgowanie i działania na potęgach
Potęgę o podstawie a i wykładniku naturalnym n oznaczamy symbolem a n i definiujemy następująco:
dla n = 1
a

a n = a ⋅ a ⋅ ⋅ ⋅ a dla n > 1 .
1
424
3
n czynników
Przykład 11. Obliczmy wartość potęg:
34 = 3 ⋅ 3 ⋅ 3 ⋅ 3 = 9 ⋅ 9 = 81,
51 = 5,
(−2) 2 = (−2) ⋅ (−2) = 4 .
Jeżeli nie ma nawiasów, to potęgowanie – jako mnożenie – wykonuje się przed
odejmowaniem, tak więc np. − 2 2 = −4 .
Niech m i n oznaczają liczby naturalne ( m, n ∈ N ). Z definicji potęgi wynikają
następujące wzory:
am ⋅ an = am+n
15
am : an =
am
an
= a m −n
dla a ≠ 0 i m > n
( a ⋅ b) n = a n ⋅ b n
n
an
a
( a : b) n =   = a n : b n = n
b
b
dla b ≠ 0
(a n ) m = a n⋅m .
Przykład 12. Obliczmy wartości wyrażeń:
23 ⋅ 22 = 23+ 2 = 25 = 32
25 : 23 = 25 − 3 = 2 2 = 4
(2 ⋅ 3) 4 = 2 4 ⋅ 34 = 16 ⋅ 81 = 1296
(2 2 )3 = 2 2⋅3 = 26 = 64
2
( )
2 6 = 23⋅ 2 = 23
= 82 = 64
(2 x) 2 = 2 2 ⋅ x 2 = 4 x 2
8 x 3 = 23 ⋅ x 3 = (2 x )3 .
1.8. Wzory skróconego mnożenia
Kwadrat sumy:
(a + b) 2 = a 2 + 2ab + b 2
Kwadrat różnicy:
(a − b) 2 = a 2 − 2ab + b 2
Sześcian sumy:
(a + b)3 = a 3 + 3a 2b + 3ab 2 + b3
Sześcian różnicy:
(a − b)3 = a 3 − 3a 2b + 3ab 2 − b3
Różnica kwadratów:
a 2 − b 2 = (a − b)(a + b)
Różnica sześcianów:
a 3 − b3 = (a − b)(a 2 + ab + b 2 )
Suma sześcianów:
a 3 + b3 = (a + b)(a 2 − ab + b 2 )
Powyższe wzory (cztery pierwsze czytane od prawej do lewej) dają możliwość przejścia
od sumy do iloczynu, inaczej mówiąc umożliwiają rozkład sumy na czynniki, co może być
16
szczególnie przydatne wtedy, gdy mianowniki ułamków chcemy rozłożyć na czynniki,
poszukując wspólnego mianownika.
Wobec powyższych wzorów nieprawdziwa jest np. równość (a ± b) 2 = a 2 ± b 2 .
Wystarczy porównać (2 + 3) 2 = 52 = 25 z 2 2 + 32 = 4 + 9 = 13 . Inaczej mówiąc kwadrat
sumy (różnicy) nie jest tym samym co suma (różnica) kwadratów.
Przykład 13. Obliczmy wartości wyrażeń (kursywą komentarz):
(2 x + 3) 2 = (2 x) 2 + 2 ⋅ (2 x) ⋅ 3 + 32 = 4 x 2 + 12 x + 9 (z uwagi na przemienność i łączność mnożenia 2 ⋅ (2 x) ⋅ 3 = 3 ⋅ 2 ⋅ (2 x) = 6 ⋅ (2 x) = 6 ⋅ 2 ⋅ x = 12 x )
(0,5 x − 2) 2 = (0,5 x) 2 − 2 ⋅ (0,5 x ) ⋅ 2 + 2 2 = 0,25 x 2 − 2 x + 4
(2 x + 3) 3 = (2 x) 3 + 3 ⋅ (2 x) 2 ⋅ 3 + 3 ⋅ (2 x) ⋅ 32 + 33 = 8 x 3 + 36 x 2 + 54 x + 27
(3 x − 2) 3 = (3x) 3 − 3 ⋅ (3x) 2 ⋅ 2 + 3 ⋅ (3x) ⋅ 2 2 − 23 = 27 x 3 − 54 x 2 + 36 x − 8
2
( ) − 3 = (x 2 − 3)(x 2 + 3)
2 x = x ⋅ 2 = x ⋅ ( 2 ) = (x 2 ) )
2x2 − 9 = x 2
2
2
2
2
2
(z uwagi na to, że 2 =
2
( 2 ) , mamy
2
8 x 3 − 1 = (2 x)3 − 13 = (2 x − 1)(4 x 2 + 2 x + 1)
8 x 3 + 1 = (2 x)3 + 13 = (2 x + 1)(4 x 2 − 2 x + 1) .
1.9. Pierwiastkowanie
Niech n ∈ N oraz a ≥ 0 . Pierwiastek stopnia n z liczby a określamy następująco:
n
a = p ⇔ pn = a i p ≥ 0 .
Pierwiastek stopnia drugiego nazywamy kwadratowym, stopnia trzeciego –
sześciennym.
Przykład 14. Obliczmy wartości pierwiastków:
4 = 4 = 2 , ponieważ 2 2 = 4 (w przypadku pierwiastka kwadratowego możemy nie
pisać stopnia pierwiastka);
2
3
8 = 2 , ponieważ 23 = 8 .
Z definicji pierwiastka wynika, że np.
2
( 7)
= 7,
3
6
( 9 ) = 9, ( 2 )
3
6
= 2.
17
Warunek p ≥ 0 w określeniu pierwiastka został wprowadzony po to, aby pierwiastkowanie było działaniem jednoznacznym. Przykładowo, dzięki temu warunkowi
a nie
4 = 2,
2
4 = ±2 (chociaż (− 2) = 4 ).
Działania na pierwiastkach
Z określenia pierwiastka wynikają następujące wzory:
n
a ⋅b = n a ⋅ n b
n
a
=
b
n m
n
n
a
n
b
dla a ≥ 0 i b ≥ 0
dla a ≥ 0 i b > 0
a = n⋅ m a
am =
dla a ≥ 0
( a)
n
m
dla a ≥ 0 .
( a)
n
= a . Nie jest nato-
a ± b = a ± b . Wystarczy porównać np.
25 − 16 = 9 = 3
Z ostatniego wzoru i definicji pierwiastka wynika, że
miast prawdziwa równość
z
n
25 − 16 = 5 − 4 = 1 .
16 ⋅ 25 ⋅ 81 = 16 ⋅ 25 ⋅ 81 = 4 ⋅ 5 ⋅ 9 = 20 ⋅ 9 = 180
121
121 11
=
=
169
169 13
3
3
6
64 = 3⋅2 64 = 26 = 2
2
64 = 3 8 2 =  3 2 3  = 2 2 = 4


81a 2b 4c 2
81 ⋅ a 2 ⋅ b 4 ⋅ c 2 9ab 2c 3ab 2c
=
=
=
36
6
2
36
2 ⋅3 3 ⋅4 4 = 2 ⋅3 3 ⋅2 2 4 = 2 ⋅3 3 ⋅ 2 = 2⋅3 3 .
an =
n
18
1.10. Wartość bezwzględna (moduł) liczby
Wartość bezwzględną liczby x oznaczamy symbolem x i określamy następująco:
dla
x
x =
−
x
dla

x≥0
x<0
.
Przykład 16. Obliczmy wartości bezwzględne liczb:
77 = 77,
− 8 = 8,
0 =0.
Niezależnie od tego, czy liczba jest dodatnia czy ujemna, moduł tej liczby jest zawsze
dodatni.
Z definicji wartości bezwzględnej oraz pierwiastka stopnia n wynika, że wzór:
x2 = x
jest prawdziwy dla każdego x ∈ R . Przykładowo
72 = 7 = 7 ,
(−7) 2 = − 7 = 7 .
1.11. Pierwiastek nieparzystego stopnia z liczby
ujemnej
Niech n będzie nieparzystą liczbą naturalną, zaś a liczbą ujemną. Przyjmuje się, że:
n
a = −n a .
Przykład 17. Obliczmy wartości pierwiastków:
3
− 8 = − 3 − 8 = − 3 8 = − 3 2 3 = −2 ,
5
− 32 = − 5 − 32 = − 5 25 = −2 .
Uwaga: pierwiastek stopnia parzystego z liczby ujemnej nie jest określony w zbiorze
liczb rzeczywistych, tzn. nie istnieje np.
− 4 . Gdyby przyjąć, że
− 4 = p , to zgodnie
z definicją pierwiastka musiałaby zachodzić równość p 2 = −4 , a to jest niemożliwe.
Niezależnie od tego, czy p jest liczbą dodatnią, zerem czy liczbą ujemną, to jej kwadrat
nie może być liczbą ujemną.
19
1.12. Potęga o wykładniku rzeczywistym
W rozdziale 1.7 mówiliśmy o potędze naturalnej, teraz rozszerzymy potęgowanie na
inne wykładniki.
Potęga o wykładniku całkowitym ujemnym
1
a−n = n
df a
Potęga o wykładniku będącym odwrotnością liczby naturalnej n
1
an = n a
df
Potęga o wykładniku wymiernym
m
a n =  a n  =
df 

1
m
a
− mn
1
=  a n 
df 

( a)
n
−m
=
m
= n am
1
 a 
 
1
n
m
=
dla a ≥ 0,
1
n
am
m, n ∈ N
dla a > 0,
m, n ∈ N
Ponieważ każdą liczbę niewymierną można przybliżyć z dowolną dokładnością liczbą
wymierną (np. 2 ≈ 1,4142 z dokładnością do czterech cyfr po przecinku), również potęga
o dowolnym wykładniku rzeczywistym może być przybliżona potęgą o wykładniku
wymiernym:
a
2
≈ a1, 4142 .
1
pozostaną prawan
dziwe, jeśli jako wykładniki m i n będziemy brać dowolne liczby rzeczywiste, a nie tylko
liczby naturalne.
Wzory z paragrafu 1.7 ( a m ⋅ a n = a m + n itd.) oraz wzór a − n =
a) 3− 2 =
b)
1 −3
2
()
1
3
1
3
=
2
=
1
1 3
2
()
3
1
9
=
1
1
8
= 1 ⋅ 81 = 8
c) 8 = 3 8 = 23 = 2
20
3
4
d) 2 4 = 23 = 4 8
e) 2
− 34
1
=
2
1
=
3
4
4
.
8
Przykład 19. Obliczmy wartość wyrażenia:
3
64 ⋅
(43 )0,75 ⋅ 2− 0,75 = (2 ⋅ 3)0,75 ⋅ (43 )0,75 ⋅ 2− 0,75 = 20,75 ⋅ 2−0,75 ⋅ 30,75 ⋅ 3−0,75 ⋅ 40,75 =
3 2
0
=
0
2 ⋅3 ⋅ 4
3 2
0,75
4
=
3 2
3
4
2
(2 )
=
1
2
=
1
3⋅ 22
3 2
3
4
3⋅ 22
3
2
3
2
1
=
3⋅ 22
2 ⋅2
3
− 12
=
2
3 1
−
2 2
3
=
21 2
=
3 3
Przykład 20. Obliczmy wartość wyrażenia:
3
 2 13 + 4 13  − 61 + 2 13 + 4 13  =




3
2
2
3
1
1
1
1
1
1
1
2
=  2 3  + 3 2 3   4 3  + 3 2 3  4 3  +  4 3  − 6 − 6 ⋅ 2 3 − 6 ⋅ 2 3 =
 
        
2
2
1
5
4
4
1
2
= 2 + 3⋅ 2 3 ⋅ 2 3 + 3⋅ 23 ⋅ 2 3 + 4 − 6 − 3⋅ 2 ⋅ 23 − 3⋅ 2 ⋅ 2 3 =
4
5
2
5
2
5
= 3 ⋅ 2 3 + 3 ⋅ 2 3 − 3 ⋅ 2 3 − 3 ⋅ 2 ⋅ 2 3 = 3 ⋅ 2 3 − 3 ⋅ 21 ⋅ 2 3 = 3 ⋅ 2 3 − 3 ⋅ 2 3 = 0
1.13. Działania na wyrażeniach niewymiernych
Dzielenie przez liczbę niewymierną jest działaniem skomplikowanym rachunkowo.
Czasami można przekształcić wyrażenie z liczbą niewymierną w mianowniku w wyrażenie
o tej samej wartości z liczbą wymierną w mianowniku. Nazywa się to usuwaniem
niewymierności z mianownika (w liczniku może pozostać wyrażenie niewymierne).
Przykład 21. Usunąć niewymierność z mianownika:
a)
b)
c)
1
2
1
3
2
2
=
2⋅ 2
3
=
3
3
a+ b
=
2
2
3
4
2⋅ 4
1
=
=
3
4
2⋅4
3
=
3
4
8
3
=
a− b
(
a+ b
)(
a− b
3
=
4
23
3
=
4
2
a− b
) ( a) −( b)
2
2
=
a− b
.
a −b
21
1.14. Relacje
W zbiorze liczb rzeczywistych określone są dwie relacje:
•
•
relacja równości oznaczana symbolem =
relacja mniejszości oznaczana symbolem <
Dla każdych dwóch liczb rzeczywistych x, y ∈ R zachodzi dokładnie jedna z trzech
możliwych sytuacji:
x= y
albo x < y
albo
(czytamy: x jest równe y )
(czytamy: x jest mniejsze od y )
y < x (czytamy: y jest mniejsze od x ).
Ostatnia relacja mniejszości może być także zapisana jako x > y (czytamy: x jest
większe od y ).
Zapis x > 0 ( x < 0 ) czytamy: x jest liczbą dodatnią (ujemną).
Wychodząc od omówionych relacji można określić dodatkowe relacje w zbiorze liczb
rzeczywistych:
x≠ y
x jest różne od y
x≤ y
x jest mniejsze od y lub równe y ( x jest niewiększe od y, x jest co
najwyżej równe y )
x≥ y
x jest większe od y lub równe y ( x jest niemniejsze od y, x jest co
najmniej równe y ).
Nierówności typu „<” lub „>” nazywamy nierównościami ostrymi, natomiast
nierówności typu „ ≤ ” lub „ ≥ ” nazywamy nierównościami nieostrymi.
Zapis x ≥ 0 ( x ≤ 0 ) czytamy: x jest liczbą nieujemną (niedodatnią).
Kilka przykładów relacji:
sin 300 > cos 900
(bo sin 300 =
log 2 1 < sin 900
(bo log 2 1 = 0 , a sin 900 = 1 ),
log 10 = 20
(bo log 10 = log10 10 = 1 i 2 0 = 1 ).
1
2
, a cos 900 = 0 ),
Jeśli chcemy porównać dwa ułamki, musimy sprowadzić je do wspólnego mianownika,
a następnie porównać ich liczniki.
22
Przykład 22. Która z liczb
2 3
i
jest większa?
3 5
Wspólny mianownik: 3 ⋅ 5 = 15 . Ponieważ
2 10
3 9
2 3
=
,a =
, więc > .
3 15
5 15
3 5
Relacje można mnożyć stronami przez tę samą wielkość. Jeśli jest to wielkość dodatnia,
relacja nie ulegnie zmianie, natomiast w wyniku pomnożenia stronami przez wielkość
ujemną relacje „<”, „ ≤ ” zmienią się odpowiednio na „>”, „ ≥ ”, np. a ≤ b ⇔ 5a ≤ 5b ,
a > b ⇔ −3a < −3b .
Często mnożenie stronami ma na celu pozbycie się mianownika ułamka. Jednak
zgodnie z tym, co zostało powiedziane wyżej, można pomnożyć stronami równość
6
= 3 przez x − 2 , otrzymując równość 6 = 3( x − 2) , natomiast nie można tego samego
x−2
6
zrobić w przypadku nierówności
< 3 , ponieważ wielkość x − 2 nie ma ustalonego
x−2
znaku: może być dodatnia (np. dla x = 7 ) lub ujemna (np. dla x = 1 ). Można natomiast
6
pomnożyć stronami nierówność
< 3 przez x 2 + 2 , otrzymując nierówność
x2 + 2
6 < 3( x 2 + 2) , ponieważ niezależnie od x (dodatniego, ujemnego czy równego zeru)
wielkość x 2 + 2 jest dodatnia (kwadrat dowolnej liczby jest liczbą nieujemną, a ta
powiększona o 2 staje się liczbą dodatnią).
Uwaga. Można mnożyć stronami relacje, nie można natomiast mnożyć danego
wyrażenia tylko dlatego, że jest ono ułamkiem, żeby pozbyć się mianownika tego ułamka,
ponieważ zmieniamy wtedy wartość tego wyrażenia. Chyba że jest to mnożenie przez 1,
1
gdy licznik i mianownik mnożymy przez tę samą liczbę. I tak mnożąc liczbę
przez
2
1
2 otrzymujemy 1, ale nieprawdą jest, że
= 1 . Prawdziwe są natomiast równości
2
1
2
=
1⋅ 2
2⋅ 2
=
2
.
2
1.15. Równania i nierówności. Przedziały
Jeśli przynajmniej po jednej stronie relacji równości czy nierówności występuje
niewiadoma (najczęściej oznaczana przez x ), to można postawić pytanie, dla jakiej
(jakich) wartości niewiadomej x ta relacja jest prawdziwa. Poszukiwanie odpowiedzi na to
23
pytanie nazywa się rozwiązywaniem równania bądź nierówności. Wszystkie wartości
niewiadomej x , dla których relacja jest prawdziwa, tworzą zbiór rozwiązań. Rozwiązania
równania nazywamy też pierwiastkami równania.
Zbiór rozwiązań może być pusty, np. równanie x 2 + 2 = 0 nie ma pierwiastków,
ponieważ dla każdej wartości x lewa strona jest liczbą dodatnią, nigdy więc nie będzie
równa prawej stronie, która jest zerem. Takie równanie nazywamy sprzecznym.
Równanie może mieć dokładnie jedno rozwiązanie, np. równanie liniowe, czyli
równanie postaci ax + b = 0 , ma tylko jeden pierwiastek x = − ba , jeśli parametr a występujący w tym równaniu (tzw. współczynnik kierunkowy) jest różny od zera.
Równanie kwadratowe x 2 − 7 x + 10 = 0 jest spełnione tylko wtedy, gdy weźmiemy
x = 2 lub x = 5 , ma więc dwa pierwiastki (o równaniach kwadratowych więcej na str. 39).
Nierówności mają na ogół nieskończenie wiele rozwiązań, np. nierówność x > 4 jest
spełniona przykładowo przez 5, 8, 17,3, 100 2 i przez każdą inną liczbę, która jest
większa od 4. Zbiór rozwiązań tej nierówności tworzy tzw. przedział (4; ∞) .
Ogólnie:
przedziałem (a; ∞) nazywamy zbiór rozwiązań nierówności x > a ,
przedziałem [a; ∞) nazywamy zbiór rozwiązań nierówności x ≥ a ,
przedziałem (−∞; a) nazywamy zbiór rozwiązań nierówności x < a ,
przedziałem (−∞; a ] nazywamy zbiór rozwiązań nierówności x ≤ a .
Jeśli a a i x a i (jednocześnie) x a i (jednocześnie) x ≤ b ” itp.
Jeśli x > a i (jednocześnie) x a
często zapisujemy w postaci 
. Jeśli zbiorem rozwiązań każdej nierówności z osobna
x 0,9
Zbiorem rozwiązań układu 
jest przedział (3; ∞) .
 x>3
24
 x ≤ 1,5
Zbiorem rozwiązań układu 
jest x = 1,5 .
 x ≥ 1,5
x < 2
Zbiór rozwiązań układu 
jest pusty.
x > 3
Należy w tym miejscu zwrócić uwagę na różnicę pomiędzy zdaniem „ x < 2 i (jednocześnie) x > 3 ”, które nie jest prawdziwe dla żadnego x , a zdaniem „ x < 2 lub x > 3 ”,
które jest prawdziwe dla dowolnego x mniejszego od 2 lub większego od 3.
Rozwiązanie równania czy nierówności polega na wykonaniu operacji, które –
zmieniając postać równania bądź nierówności – nie zmieniają zbioru rozwiązań. Mówimy
wtedy, że przechodzimy do postaci równoważnej danego równania lub nierówności.
Dodanie do obu stron czy odjęcie od obu stron tej samej wielkości, pomnożenie czy
podzielenie obu stron przez te samą wielkość różną od zera są operacjami prowadzącymi
do postaci równoważnej.
Przykład 24. Rozwiązać nierówność 6 − 2 x > 0 .
Dodajemy −6 do obu stron (inaczej mówiąc przenosimy 6 na prawą stronę z przeciwnym znakiem) i otrzymujemy −2 x > −6 . Następnie dzielimy obie strony przez −2 i –
zmieniając znak nierówności - otrzymujemy x < 3 . Nierówność x < 3 jest równoważna
nierówności 6 − 2 x > 0 , tzn. obie nierówności mają ten sam zbiór rozwiązań. W takim
razie zbiorem rozwiązań nierówności 6 − 2 x > 0 jest przedział (−∞; 3) . Powyższe rozumowanie można krótko zapisać w następujący sposób:
6 − 2 x > 0 ⇔ −2 x > −6 ⇔ x < 3 .
Jeśli po jednej stronie nierówności ostrej jest iloraz dwóch wielkości, a po drugiej
stronie zero, to biorąc iloczyn tych wielkości zamiast ich ilorazu otrzymujemy nierówność
x
równoważną, np. nierówność
< 0 ma ten sam zbiór rozwiązań co nierówność
x+3
x( x + 3) < 0 .
Podniesienie obu stron do kwadratu może zwiększyć zbiór rozwiązań, np. równanie
x = 1 ma oczywiście tylko jeden pierwiastek, natomiast w równaniu x 2 = 1 dochodzi
jeszcze pierwiastek: −1 . Piszemy: x = 1 ⇒ x 2 = 1 (ale nie: x = 1 ⇔ x 2 = 1 ). Mimo to
można stosować ten sposób np. do rozwiązywania równań, w których niewiadoma
występuje pod znakiem pierwiastka kwadratowego, byleby sprawdzić, które z otrzymanych
rozwiązań są pierwiastkami równania wyjściowego.
25
2. Zadania różne
2.1. Przekształcanie wyrażeń wymiernych
Przykład 25. Rozłożyć na czynniki wyrażenia:
a) xy + yz + x + z
Rozwiązanie powinno zmierzać do takiego przekształcenia tego wyrażenia, aby było
możliwe wyłączenie przed nawias pewnych wspólnych czynników. Dość wyraźnie widać,
że z pierwszych dwóch składników można wyłączyć y, co z kolei pozwoli na wyłączenie
x+z:
xy + yz + x + z = xy + yz + ( x + z ) = y ( x + z ) + ( x + z ) = ( x + z )( y + 1) .
b) ax 2 − bx 2 + bx − ax + a − b
Rozwiązanie powinno przebiegać w kierunku takiego przekształcenia tego wyrażenia,
aby było możliwe wyłączenie wspólnego czynnika przed nawias.
ax 2 − bx 2 + bx − ax + a − b = x 2 (a − b) + x(b − a) + (a − b) =
= x 2 (a − b) + x(−1)(−b + a) + (a − b) = x 2 (a − b) − x(a − b) + (a − b) =
= (a − b)( x 2 − x + 1)
Przykład 26. Uprościć wyrażenie:
a−c
a 2 + ac + c 2
⋅
1 + c  c(1 + c) − a
a3 − c3 
c
−
.
1 +
:
2
2
c 
bc
a b − bc  a − c
Ten przykład jest trochę bardziej skomplikowany niż poprzednie. W jednym z liczników mamy różnicę sześcianów, a w mianowniku (innego ułamka) niepełny kwadrat sumy:
a 2 + ac + c 2 (pełny kwadrat sumy to a 2 + 2ac + c 2 ). Podobnie licznik pierwszego ułamka
zawiera różnicę a − c , a mianownik drugiego z ułamków możemy tak przekształcić, aby
taka różnica tam się pojawiła, co pozwoli na skrócenie ułamka. Z kolei wyrażenie
w nawiasie musimy doprowadzić do wspólnego mianownika. Kolejno otrzymujemy:
a−c
2
a + ac + c
=
2
⋅
a−c
a 2 + ac + c 2
a3 − c3 
c
1 + c  c (1 + c) − a
−
=
1 +
:
c 
bc
a 2b − bc 2  a − c
⋅
(a − c)(a 2 + ac + c 2 )  c (a − c) + c 2 − (a − c )(1 + c )  c(1 + c ) − a
:
=

b(a − c )(a + c) 
c( a − c )
bc

26
=
a − c  c((a − c) + c) − (a − c)(1 + c)  c(1 + c ) − a

 :
=
b(a + c) 
c(a − c)
bc

=
1
c(a − c + c) − (a + ac − c − c 2 ) c(1 + c) − a
⋅
:
=
b( a + c )
c
bc
1
ac − a − ac + c + c 2 c(1 + c) − a
⋅
:
=
b( a + c )
c
bc
c(1 + c) − a
bc
1
1
=
⋅
⋅
=
b( a + c )
c
c(1 + c) − a a + c
=
Zadania do samodzielnego wykonania
1. Rozłożyć na czynniki wyrażenie a 5 − a 3 + a 2 − 1 . Odp. (a − 1)(a + 1) 2 (a 2 − a + 1) .
2. Rozłożyć na czynniki wyrażenie bc(b + c) + ca (c − a ) − ab(a + b) .
Odp. (a + b)(b + c)(c − a) .
3. Uprościć wyrażenie
x 2 + 1x
x + 1x − 1
dla x ≠ 0 .
Odp. x + 1 .
2
2
 ab
 a − b a + b  a + b
4. Uprościć wyrażenie 
+
+ 1 2
dla a, b ≠ 0, a ≠ b .

 a + b2
 a + b a − b  2ab

Odp.
a+b
.
a−b
5. Uprościć wyrażenie
Odp.
1
x y
2 2
.
 1
1 
2 1 1
 +
+
 +  dla x, y ≠ 0, x ≠ − y .
2
2 

( x + y)  x
y  ( x + y )3  x y 
1
2
27
2.2. Przekształcanie wyrażeń niewymiernych
Przykład 27. Uprościć wyrażenie
(a + b) − 12 + (a − b) − 12 


−1
+ ( a + b )

− 12
( a + b )

−1
− ( a + b )

− 12
− 12
+ ( a − b)
− 12


− ( a − b)
− ( a − b)
− 12 
−1


−1

− 12
Przekształcanie tego wyrażenia musimy rozpocząć od wykorzystania wzorów na potęgę
o wykładniku rzeczywistym.
(a + b) − 12 + (a − b) − 12 


−1
+ ( a + b )

− 12
− 12 
−1
− ( a + b )

− 12
( a + b )

− 12
+ ( a − b)

− ( a − b)
− (a − b)
−1
− 12 
−1
− 12 
−1


−1
 1
 1
1 
1 
+
−

 +

a+b
a−b 
a −b 
 a+b
=
=
−1
−1
 1
 1
1 
1 
+
−

 −

a−b 
a−b 
 a+b
 a+b
−1
−1
 a−b + a+b
 a−b − a+b 

 +





a2 − b2
a 2 − b2
=
=
−1
−1
 a−b + a+b 
 a−b − a+b 

 −

a2 − b2
a2 − b2




a2 − b2
=
a−b + a+b
2
a −b
2
a−b + a+b
=
+
−
a 2 − b2
a−b − a+b =
a2 − b2
a−b − a+b

1
a 2 − b2 
+
a −b
 a−b + a+b

1
a2 − b2 
−
a
−
b
+
a+b
a−b



− a+b
=

1

− a+b
1
=
28
=
a−b − a+b + a−b + a+b
a−b − a+b − a−b − a+b
=
2 a−b
−2 a+b
=−
a−b
.
a+b
Przykład 28. Uprościć wyrażenie:
1− a2
⋅ (1 − a) 2 dla a ≤ 1
1− a a
 1 + a a


+ a 
− a
 1− a
 1 + a




Zaczniemy od przekształcenia mianownika ułamka piętrowego poprzez sprowadzenie
do wspólnego mianownika, a następnie wykorzystanie wzoru na różnicę kwadratów.
1− a2
⋅ (1 − a) 2 =
1− a a
 1 + a a


+ a 
− a
 1− a
 1 + a




=
=
=
=
1− a2
⋅ (1 − a) =
 1 − a a + a 1 − a  1 + a a − a 1 + a 






1− a
1+ a



(
)
(1 − a 2 )(1 − a)
(1 − a (a − 1) − a)(1 + a (a − 1) − a)
(
⋅ (1 − a) =
(1 − a 2 ) (1 − a) 2
(1 − a −
)(
)
)
a (a − 1) 1 − a + a (a − 1)
=
(1 − a 2 )(1 − a) 2
(1 − a) 2 −
1 − a 2 (1 − a)(1 + a)
=
=1+ a .
1− a
1− a
2
)
a (a − 1)
(1 − a 2 )(1 − a) 2
(1 − a 2 )(1 − a) 2
(1 − a 2 )(1 − a) 2
=
=
=
(1 − a) 2 − a(a − 1) 2 (1 − a) 2 − a(1 − a) 2
(1 − a) 2 (1 − a)
(wykorzystano zależność (1 − a) 2 = (a − 1) 2 )
=
(
=
29
Przykład 29. Usunąć niewymierność z mianownika w wyrażeniu:
1
1+ 2 + 3
.
Zadanie nasze polega na takim rozszerzeniu tego ułamka, aby można było zlikwidować
pierwiastki w mianowniku. Technicznie musimy mnożyć licznik i mianownik przez takie
wyrażenie, aby można było skorzystać ze wzorów na różnicę kwadratów.
W naszym przykładzie mamy:
1
1+ 2 + 3
=
1
=
(1 + 2 )+
1+ 2 − 3
2
3
((1 +
1+ 2 − 3
=
2
=
(1 + 2 ) − ( 3 )
2 (1 + 2 − 3 )
=
=
1+ 2 2 + 2 − 3
=
(1 + 2 )− 3
2 ) + 3 )((1 + 2 ) − 3 )
1+ 2 − 3
2 2
=
=
(
)
2 + 2 − 2 3 2 + 2 1− 3
2+ 2 − 6
=
=
4
4
4
2 2 2
Przykład 30. Usunąć niewymierność z mianownika w wyrażeniu:
1
2 + 5 + 2 2 + 10
.
Zaczniemy od odpowiedniego pogrupowania elementów mianownika w celu doprowadzenia do takiej sytuacji, aby było możliwe rozszerzenie ułamka likwidujące
niewymierność w mianowniku. Kolejno mamy:
1
2 + 5 + 2 2 + 10
=
=
1
2 + 5 + 2 2 + 2⋅5
1
2+2 2 + 5 + 2 5
=
(1 +
(
=
=
1
2+ 5 +2 2 + 2 5
1
(
)
(
2 1+ 2 + 5 1+ 2
)
=
1
)(
)
=
(1 + 2 )(2 + 5 )
5 ) (1 − 2 )(2 − 5 )
=
=
(1 − 2 )(2 − 5 )
(1 − 2 )(2 −
=
(1 − 2)(4 − 5)
2 )(2 + 5 )(1 − 2 )(2 − 5 )
= 1− 2 2 − 5 .
=
1
30
Zadania do samodzielnego wykonania
6. Uprościć wyrażenie:

 1
1+ a
1− a
1


− 1 −  dla 0 < a < 1 .
+
2

 1+ a − 1− a

a 
1− a2 −1+ a  a

Odp. −1 .
 4 a 3 − 4 b3
 a


− 4 a − 4 b   4 + 1

 a− b
 b



dla a > 0, b > 0, a ≠ b .
Odp. − 4 a .
a − 2 a +1
4
a − 2 a +1
4
:4
a +1
a −1
+1 .
Odp. 0 dla 0 < a < 1 , 2 dla a > 1 .
9. Usunąć niewymierność z mianownika:
1
3
3
2+ 2 + 4
Odp. 1− 12 3 4 .
.
1
dla a ≥ b > 0 .
a − a2 − b2
.
b
Odp.
a + a 2 − b2
1
10 − 15 + 14 − 21
.
Odp.
(
3+ 2
)(
2
5− 7
).
31
2.3. Rozwiązywanie równań i nierówności liniowych
Przykład 31. Rozwiązać równanie:
y−
20 y − (10 − 3 y ) 26 y − 51 2(1 − 3 y )
=
−
.
156
52
13
Przy rozwiązywaniu równań liniowych (czyli takich, w których niewiadoma występuje
w pierwszej potędze) tak przekształcamy wyrażenie, aby po lewej stronie znaku równania
otrzymać niewiadomą, a po prawej odpowiadającą jej liczbę. W naszym przykładzie
zaczniemy od zlikwidowania ułamków mnożąc obie strony równania przez wspólny
mianownik (tu 156), a następnie uporządkujemy wyrażenie. Kolejno otrzymujemy:
20 y − (10 − 3 y ) 26 y − 51 2(1 − 3 y )
=
−
⋅ 156
156
52
13
156 y − (20 y − (10 − 3 y ) ) = 3(26 y − 51) − 12 ⋅ 2(1 − 3 y )
156 y − (20 y − 10 + 3 y ) = 78 y − 153 − 24(1 − 3 y )
156 y − 23 y + 10 = 78 y − 153 − 24 + 72 y
133 y − 78 y − 72 y = −10 − 153 − 24
y−
− 17 y = −187 ⋅ (− 17 )
y = 11
Sprawdzenie rozwiązania:
L = 11 −
20 ⋅ 11 − (10 − 3 ⋅ 11)
= 11 −
220 − (10 − 33)
156
156
11 ⋅ 156 − 243 1716 − 243 1473
=
=
=
156
156
156
P=
=
26 ⋅ 11 − 51
52
705 + 768
156
L=P.
=
−
2(1 − 3 ⋅ 11)
1473
156
13
=
286 − 51
52
−
= 11 −
2(1 − 33)
13
=
220 + 23
235
52
156
−
−64
13
= 11 −
=
243
156
=
235 ⋅ 3 + 64 ⋅ 12
156
=
32
Przykład 32. Rozwiązać równanie:
1
2
x + 2x +1
4
+
2
x + 2x + x
=
3
5
2x + 2x2
.
Działania, które powinniśmy podjąć rozwiązując to równanie, powinny zmierzać do
zlikwidowania ułamków. Można to zrealizować mnożąc obustronnie to równanie przez
wspólny mianownik. Przed jego wyznaczeniem warto zauważyć, że z mianownika
drugiego z ułamków możemy wyciągnąć przed nawias x, a z mianownika trzeciego ułamka
wyrażenie 2x. Dodatkowo zauważmy, że x 2 + 2 x + 1 jest równe ( x + 1) 2 , co znakomicie
ułatwia ustalenie wspólnego mianownika dla wszystkich trzech ułamków. Kolejno mamy:
1
+
4
2x2
=
5
+ 2x + 1 x +
+
2x + 2x2
1
4
5
+
=
⋅ 2 x ( x + 1) 2
2
2
2 x(1 + x)
( x + 1) x( x + 1)
2 x + 4 ⋅ 2 = 5( x + 1)
x2
x3
2 x + 8 = 5x + 5
2 x − 5x = 5 − 8
− 3 x = −3 : (−3)
Rozwiązanie: x = 1 .
Sprawdzenie rozwiązania:
L=
P=
1
+
4
1+ 2 +1 1+ 2 +1
5
2+2
=
=
1
4
+1 =
1
4
+
4
4
=
1+ 4
4
=
5
4
5
4
L=P.
Przykład 33. Dla jakich wartości t prawdziwa jest nierówność:
6(t 2 + t + 1) > (t + 1)3 − (t − 1)3 .
Zaczniemy rozwiązywanie tej nierówności od podniesienia do trzeciej potęgi wyrażeń
po prawej stronie znaku większości, zlikwidowania nawiasu po stronie lewej oraz uporządkowania nierówności.
33
Kolejno mamy:
6(t 2 + t + 1) > (t + 1) 3 − (t − 1) 3
6t 2 + 6t + 6 > t 3 + 3t 2 + 3t + 1 − (t 3 − 3t 2 + 3t − 1)
6t 2 + 6t + 6 > t 3 + 3t 2 + 3t + 1 − t 3 + 3t 2 − 3t + 1
6t 2 + 6t + 6 > 6t 2 + 2
6t > 2 − 6
6t > −4 : 6
t > − 46
Rozwiązanie: t > − 23 .
Przykład 34. Dla jakich wartości x prawdziwa jest nierówność:
2+
1
4 − 8x
>
.
x −3
x −3
Przy rozwiązywaniu tej nierówności nie wolno nam pomnożyć jej obu stron przez
wyrażenie x − 3 (w celu zlikwidowania ułamka), ponieważ nie jest ustalony znak tego
wyrażenia. Zaczniemy od przeniesienia niewiadomych na lewą stronę znaku nierówności
tak, aby po prawej stronie pozostało zero. Kolejno mamy:
1
4 − 8x
2( x − 3) + 1 4 − 8 x
>
⇔
−
>0 ⇔
x−3
x−3
x−3
x−3
2 x − 6 + 1 − 4 + 8x
10 x − 9
⇔
>0 ⇔
>0
x −3
x −3
2+
10 x − 9
> 0 wtedy i tylko wtedy, gdy jego licznik i mianownik są tych samych
x−3
znaków. Otrzymujemy stąd dwa układy dwóch nierówności liniowych:
Ułamek
10 x − 9 > 0
10 x − 9 < 0
lub 
.

 x −3 > 0
 x −3 < 0
Rozwiązując kolejno oba układy otrzymujemy:
10 x − 9 > 0
⇔ 10 x − 9 > 0 ∧ x − 3 > 0 ⇔ x > 0,9 ∧ x > 3 ⇔ x > 3

 x−3> 0
10 x − 9 < 0
⇔ 10 x − 9 < 0 ∧ x − 3 < 0 ⇔ x < 0,9 ∧ x < 3 ⇔ x < 0,9 .

 x−3< 0
34
Ostatecznie rozwiązaniem naszej nierówności są x < 0,9 lub x > 3 .
Użyty w powyższym rozwiązaniu symbol „ ∧ ” jest tym samym co spójnik „i”.
Podobnie symbol „ ∨ ” jest tym samym co spójnik „lub”. Ostateczne rozwiązanie tej
nierówności można więc zapisać także w postaci: x < 0,9 ∨ x > 3 .
x−3 > 7 .
Korzystając ze wzorów dotyczących nierówności z modułem
x p ⇔ x < −p ∨ x > p
mamy:
x − 3 > 7 ⇔ x − 3 < −7 ∨ x − 3 > 7 ⇔ x < −4 ∨ x > 10 .
Odp. Nierówność x − 3 > 7 jest prawdziwa dla x < −4 ∨ x > 10 .
x +1 − x > 0 .
Wyrażenia w modułach zmieniają znak w otoczeniu punktów –1 i 0, stąd musimy
rozpatrywać tę nierówność dla x-ów z trzech przedziałów: x < −1 , −1 ≤ x < 0 , x ≥ 0 .
Dla x < −1 jest x + 1 < 0 i x < 0 . Mamy wtedy:
−( x + 1) − ( − x ) > 0 ⇔ − x − 1 + x > 0 ⇔ −1 > 0 – nierówność sprzeczną.
Dla −1 ≤ x < 0 mamy x + 1 ≥ 0 oraz x < 0 , stąd:
( x + 1) − ( − x ) > 0 ⇔ 2 x > −1 ⇔ x > −0,5 .
Dla x ≥ 0 mamy:
( x + 1) − x > 0 ⇔ x + 1 − x > 0 ⇔ 1 > 0 – nierówność prawdziwa.
Żadne x z przedziału (−∞, − 1) nie spełnia nierówności x + 1 − x > 0 , w przedziale
[−1, 0) nierówność ta spełniona jest dla x > −0,5 , a z przedziału [0, + ∞) nierówność
spełniają wszystkie x .
Ostatecznie rozwiązaniem naszej nierówności są więc x > −0,5 .
35
Przykład 37. Ile należy wziąć kg srebra próby 0,7 i ile kg srebra próby 0,9 , aby otrzymać
4 kg stopu próby 0,85 ?
Oznaczmy symbolem x ilość srebra próby 0,7 , a przez 4 − x ilość srebra próby 0,9 .
W x kilogramach srebra próby 0,7 czystego srebra jest 0,7 x . Analogicznie w 4 − x
kilogramach srebra próby 0,9 czystego srebra jest 0,9(4 − x) . W 4 kg stopu próby 0,85
czystego srebra będzie 0,85 ⋅ 4 = 3,4 . Ostatecznie potrzebne ilości obu stopów srebra
znajdziemy rozwiązując następujące równanie:
0,7 x + 0,9(4 − x)
= 0,85
4
0,7 x + 0,9(4 − x ) = 4 ⋅ 0,85
0,7 x + 3,6 − 0,9 x = 3,4
− 0,2 x = −3,6 + 3,4
− 0,2 x = −0,2
x =1
Odp. Musimy wziąć 1 kg srebra próby 0,7 i 3 kg srebra próby 0,9 w celu otrzymania
4 kg srebra próby 0,85 .
Przykład 38. Rozwiążmy układ dwóch równań liniowych postaci:
6 x + y = 0

2 x + 2 = 4 − x − y
Rozwiązaniem układu dwóch równań liniowych jest taka para wartości x,y, która
spełnia oba równania. Układ dwóch równań liniowych może mieć:
• jednoznaczne rozwiązanie (jedna para wartości x,y),
• brak rozwiązań (nie istnieje taka para x,y, która spełnia oba równania
jednocześnie – choć może spełniać jedno z tych równań),
• nieskończenie wiele rozwiązań (nieskończenie wiele par x,y spełniających oba
równania).
Istnieje kilka metod rozwiązywania układów dwóch równań liniowych. Do najczęściej
używanych można zaliczyć metodę podstawiania oraz metodę przeciwnych współczynników. Tę ostatnią metodę wykorzystamy do rozwiązania naszego układu równań.
6 x + y = 0

2 x + 2 = 4 − x − y
6 x + y = 0

3 x + y = 2 ⋅ (−1)
36
6 x + y = 0

 − 3 x − y = −2
po dodaniu stronami
⇒
3 x = −2 ⇒ x = −
2
.
3
Wyznaczoną wartość x wstawiamy do jednego z równań w celu obliczenia wartości
drugiej niewiadomej:
 2
6 ⋅ −  + y = 0 ⇒ y = 4 .
 3
Ostatecznie rozwiązaniem układu równań jest x = − 23 , y = 4 .
Przykład 39. W prostokątnym układzie współrzędnych X0Y na płaszczyźnie zaznaczyć
punkty, których współrzędne spełniają układ nierówności:
2 x + y − 2 ≥ 0

x − 2 y + 2 ≤ 0
Rozwiązanie tego typu zadań można zacząć od przekształcenia każdej nierówności do
postaci y ≥ ax + b lub y ≤ ax + b . Punkty płaszczyzny, których współrzędne x, y
spełniają nierówność y ≥ ax + b , położone są na prostej o równaniu y = ax + b i powyżej
tej prostej. Punkty płaszczyzny, których współrzędne x, y spełniają nierówność
y ≤ ax + b , położone są na prostej o równaniu y = ax + b i poniżej tej prostej.
W naszym przykładzie zaczynamy od przekształcenia obu nierówności do postaci
y ≥ ax + b oraz y ≤ cx + d , co pozwoli nam na naszkicowanie wykresów obu funkcji
liniowych i zaznaczenie punktów o współrzędnych spełniających każdą z nierówności.
 y ≥ −2 x + 2
2 x + y − 2 ≥ 0
 y ≥ −2 x + 2
⇔
⇔

x − 2 y + 2 ≤ 0
 y ≥ 0,5 x + 1
− 2 y ≤ − x − 2 : (−2)
l2 : y = 0,5 x + 1
l1 : y = −2 x + 2
37
Zadania do samodzielnego rozwiązania
12. Rozwiązać równanie
1
2
(3 − 2 y )
−
3
9 − 4y
2
=
4
(3 + 2 y )2
.
Odp. y = 0,9 .
13. Rozwiązać równanie ( x + 2)( x − 3) = ( x − 5)( x − 6) .
Odp. x = 3,6 .
3− x
1
+
= 2.
x−2 2− x
3
x2 −1
−
Odp. Równanie sprzeczne.
2x
5x
2x
=
−
.
x + 1 x2 −1 x − 1
Odp. x = 3 .
16. Masa wodoru zawartego w wodzie stanowi 12,5% masy zawartego w niej tlenu. Ile
kg wodoru i ile kg tlenu znajduje się w 8,1 kg wody?
Odp. 0,9 kg wodoru i 7,2 kg tlenu.
17. Ile gramów stopu 30% i ile gramów stopu 70% należy zmieszać, aby otrzymać 500
gram stopu 60%?
Odp. Odpowiednio 125 i 375 gramów obu stopów.
18. Rozwiązać nierówność 4 x − 3 < x + 6 .
19. Rozwiązać nierówność
4x + 1 x + 4
>
.
2
5
Odp. x < 3 .
Odp. x >
1
.
6
20. Rozwiązać nierówność ( x + 5)(4 − x) > 0 .
Odp. −5 < x < 4 .
21. Rozwiązać nierówność (3 x − 1) 2 + (4 x − 1) 2 < (5 x − 1) 2 .
Odp. x > 0,25 .
3x − 15
< 0.
x−2
2x +1
>1.
x+2
Odp. 2 < x < 5 .
Odp. x < −2 lub x > 1 .
38
 x − 5y = 1
24. Rozwiązać układ równań 
.
x + 2 y = 2
Odp. x = 127
y = 17 .
 2x − y = 3 + x
25. Rozwiązać układ równań 
.
 x − 0,5 y = 3 + 0,5 x
Odp. Brak rozwiązań, układ sprzeczny.
26. Po zmieszaniu dwóch roztworów kwasu solnego 75% i 54% otrzymano 42 litry
roztworu 66%. Jakie ilości roztworów o stężeniu 75% i 54% zmieszano?
Odp. Odpowiednio 24 i 18 kg kwasu obu stężeń.
27. W prostokątnym układzie współrzędnych X0Y na płaszczyźnie wyznaczyć punkty,
których współrzędne spełniają układ nierówności:
y < 3

 y − 6 > −2 x
28. W prostokątnym układzie współrzędnych X0Y na płaszczyźnie wyznaczyć punkty,
y < 3

 y − 6 > −2 x
x ≤ 5

29. W prostokątnym układzie współrzędnych X0Y na płaszczyźnie zaznaczyć punkty,
 2x + y − 2 ≤ 0
4 x + 2 y + 1 > 0

 2x + y − 2 > 0
4 x + 2 y + 1 < 0

2 x + y − 2 > 0
x > 3

39
2.4. Rozwiązywanie równań i nierówności
kwadratowych
Przykład 40. Rozwiązać równanie
2x +1 x −1
x+3 4+ x
− 2
=
−
.
x +3 x −9 3− x 3+ x
Zaczniemy od przekształcenia tego równania, tak by doprowadzić je do prostszej, ale
równoważnej postaci:
2x +1
−
x+3
2x +1
−
x+3
x −1
x +3 4+ x
−
x −9 3− x 3+ x
x −1
x+3 4+ x
=−
−
⋅ ( x + 3)( x − 3)
2
x −3 3+ x
x −9
2
=
(2 x + 1)( x − 3) − ( x − 1) = −( x + 3) 2 − (4 + x)( x − 3)
2 x 2 − 6 x + x − 3 − x + 1 = − x 2 − 6 x − 9 − 4 x + 12 − x 2 + 3x
4x2 + x − 5 = 0
Otrzymaliśmy równanie
następująco:
kwadratowe, którego ogólną postać
można zapisać
ax 2 + bx + c = 0, gdzie a ≠ 0 .
Wyrażenie ax 2 + bx + c nazywamy trójmianem kwadratowym.
Wyróżnik ∆ = b 2 − 4ac decyduje o liczbie pierwiastków (czyli rozwiązań) równania
kwadratowego:
−b− ∆
−b+ ∆
, x2 =
2a
2a
∆>0:
2 pierwiastki
x1 =
∆=0:
1 pierwiastek podwójny
x1 = x2 =
∆ < 0:
brak pierwiastków.
−b
2a
W przypadku równania 4 x 2 + x − 5 = 0 mamy:
∆ = 12 − 4 ⋅ 4 ⋅ (−5) = 81 ,
Stąd x1 =
−1 − 9
10
5
=− =− ,
2⋅4
8
4
∆ = 81 = 9 .
x2 =
−1 + 9 8
= =1.
2⋅4
8
Tak więc równanie 4 x 2 + x − 5 = 0 ma dwa pierwiastki: x1 = − 54 , x2 = 1 .
40
Sprawdzenie:
Dla x = x1 = − 54 mamy L = 4 ⋅ (−
5 2
4
)
+ (− 54 ) − 5 =
25
4
− 54 − 5 =
20
4
−5=5−5 = 0 = P.
Dla x = x2 = 1 mamy L = 4 ⋅ 12 + 1 − 5 = 4 + 1 − 5 = 5 − 5 = 0 = P .
Ponieważ wyjściowe równanie jest równoważne równaniu 4 x 2 + x − 5 = 0 , więc ma te
same pierwiastki. Sprawdzenie tego pozostawiamy jako samodzielne ćwiczenie.
Przykład 41. Rozwiązać równanie 12 x 2 + 7 x = 0 .
W tym przykładzie mamy taką sytuację (w odniesieniu do postaci ogólnej), że
współczynnik c jest zerowy. Jest to jedna z tzw. postaci równania kwadratowego
niezupełnego. Rozwiążemy to równanie poprzez wyciągniecie przed nawias wielkości ax .
W przykładzie mamy kolejno:
7
7

12 x 2 + 7 x = 0 ⇔ 12 x x +  = 0 ⇔ 12 x = 0 ∨ x +
=0 ⇔
12
12


7
x=0 ∨ x=−
12
Przykład 42. Rozwiązać równanie x 2 − 49 = 0 .
Jest to kolejna postać równania kwadratowego niezupełnego, tym razem ax 2 + c = 0 .
Równanie to ma rozwiązania tylko wtedy, gdy a ⋅ c ≤ 0 . Klasyczna technika
rozwiązywania polega na wykorzystaniu wzoru na różnicę kwadratów. W przykładzie
mamy:
x 2 − 49 = 0 ⇔ x 2 − 7 2 = 0 ⇔ ( x + 7)( x − 7) = 0 ⇔ x = −7 ∨ x = 7 .
Przykład 43. Rozwiązać równanie x 2 + 4 = 0 .
Zgodnie z uwagą sformułowaną w przykładzie 42 równanie to nie ma pierwiastków
( a ⋅ c = 1 ⋅ 4 = 4 > 0 ). Wynika to również z tego, że ∆ = 0 2 − 4 ⋅ 1 ⋅ 4 = −16 < 0 .
Przykład 44. Dla jakich x spełniona jest nierówność 5 x 2 − 7 x + 2 > 0 .
Rozwiązanie nierówności 5 x 2 − 7 x + 2 > 0 wymaga przedstawienia lewej strony jako
tzw. postaci iloczynowej trójmianu kwadratowego: ax 2 + bx + c = a( x − x1 )( x − x2 ) .
Mamy ∆ = (−7) 2 − 4 ⋅ 5 ⋅ 2 = 49 − 40 = 9,
Stąd x1 =
−(−7) − 3
2⋅5
=
4
10
= 0,4 ,
x2 =
∆ = 9 = 3.
− ( −7 ) + 3
2⋅5
=
10
10
=1.
41
Możemy już zapisać naszą nierówność w postaci:
5 x 2 − 7 x + 2 > 0 ⇔ 5( x − 0,4)( x − 1) > 0 .
Rozwiązanie nierówności 5( x − 0,4)( x − 1) > 0 najłatwiej znaleźć korzystając z wykresu
funkcji kwadratowej. Jak wiadomo, wykresem tej funkcji jest parabola o gałęziach skierowanych do góry dla a > 0 lub do dołu dla a < 0 .
y = 5x2 − 7 x + 2
+
+
0,4
−
1,0
Z wykresu widać, że wartości dodatnie funkcja y = 5 x 2 − 7 x + 2 przyjmuje dla x < 0,4
lub dla x > 1 .
Odp. Nierówność 5 x 2 − 7 x + 2 > 0 spełniona jest dla x < 0,4 lub dla x > 1 .
Przykład 45. Dla jakich x spełniona jest nierówność
−3 x
x+2
<0
Jedną z łatwiejszych metod rozwiązywania nierówności tego typu jest wykorzystanie
faktu, że znak ilorazu jest taki sam jak iloczynu. Mamy więc:
−3 x
x+2
< 0 ⇔ −3 x( x + 2) < 0 .
Po sporządzeniu szkicu wykresu trójmianu
kwadratowego y = −3x( x + 2) widzimy, że
wartości ujemne funkcja ta przyjmuje dla
x < −2 lub x > 0 .
Odp. Nierówność
dla x < −2 ∨ x > 0 .
−3 x
x+2
< 0 spełniona jest
y = −3 x ( x + 2 )
+
−2
0
−
−
42
Przykład 46. Dla jakiej wartości parametru m równanie:
(m + 2) x 2 + 6mx + 4m − 1 = 0
ma dwa różne pierwiastki ujemne?
Na to, aby równanie kwadratowe ax 2 + bx + c = 0 miało dwa różne pierwiastki ujemne
muszą być spełnione jednocześnie trzy warunki:
I . ∆ = b 2 − 4ac > 0
II . x1 + x2 =
−b− ∆
2a
+
−b+ ∆
2a
=
−b
a
<0
 − b − ∆  − b + ∆  b 2 − ∆ b 2 − b 2 + 4ac c

=
III . x1 ⋅ x2 = 
=
= >0.
 2a  2a 
a
4a 2
4a 2



W naszym przykładzie mamy a = m + 2 , b = 6m i c = 4m − 1 . Rozwiązujemy pierwszy
warunek:
I . ∆ = 36m 2 − 4(m + 2)(4m − 1) > 0 . Mamy
36m 2 − 4(4m 2 − m + 8m − 2) > 0 ⇒ 9m 2 − 4m 2 − 7 m + 2 > 0 ⇒
⇒ 5m 2 − 7 m + 2 > 0
Nierówność 5m 2 − 7 m + 2 > 0 jest analogiczna do nierówności z przykładu 42 (z m
zamiast x ), możemy więc od razu zapisać jej rozwiązanie:
5m 2 − 7 m + 2 > 0 ⇔ m < 0,4 ∨ m > 1 .
Tym samym dla takich wartości parametru m istnieją dwa różne pierwiastki. Dwa
dodatkowe warunki są po to, aby były to pierwiastki dodatnie. Kolejno je rozwiążemy, a na
koniec poszukamy wspólnego rozwiązania dla tych trzech warunków.
II . x1 + x2 =
−b
a
=
−6m
( m + 2)
< 0 ⇒ −6m(m + 2) < 0 ⇒ m(m + 2) > 0 .
Nierówność m(m + 2) > 0 jest równoważna nierówności −3x( x + 2) < 0 rozpatrywanej
w przykładzie 45, a jej rozwiązaniem są wartości m < −2 ∨ m > 0 .
III . x1 ⋅ x2 =
c 4m − 1
=
> 0 ⇒ 4(m − 0,25)(m + 2) > 0 .
a m+2
43
y = 4( m − 0,25)(m + 2)
+
+
−
−2
0,25
Nierówność 4( m − 0,25)(m + 2) > 0 jest spełniona dla m < −2 lub m > 0,25 .
Zestawiamy wszystkie trzy rozwiązania na wspólnej osi liczbowej:
-2
0,4
1
Ostatecznie równanie (m + 2) x 2 + 6mx + 4m − 1 = 0 będzie miało dwa różne pierwiastki
ujemne dla m < −2 lub m > 1 .
Przykład 47. Rozwiązać równanie x 4 − 5 x 2 + 4 = 0 .
Jest to przykład tzw. równania dwukwadratowego, które rozwiązujemy poprzez
wprowadzenie nowej zmiennej w taki sposób, aby sprowadzić je do standardowego
równania kwadratowego. W naszym przykładzie podstawiając x 2 = t otrzymamy:
t 2 − 5t + 4 = 0
∆ = (−5) 2 − 4 ⋅1⋅ 4 = 26 − 16 = 9
t1 =
−(−5) − 3 5 − 3
=
=1
2 ⋅1
2
∆ = 9 =3
t2 =
−(−5) + 3 5 + 3
=
=5.
2 ⋅1
2
Wracamy do podstawienia:
x 2 = t1 = 1 ⇔ x 2 − 1 = 0 ⇔ ( x + 1)( x − 1) = 0 ⇔ x = −1 ∨ x = 1 ,
x 2 = t 2 = 4 ⇔ x 2 − 4 = 0 ⇔ ( x + 2)( x − 2) = 0 ⇔ x = −2 ∨ x = 2 .
Ostatecznie pierwiastkami równania x 4 − 5 x 2 + 4 = 0 są liczby −2, − 1, 1, 2 .
44
Przykład 48. Rozwiązać równanie x + 10 x + 6 = 9 .
Jest to przykład równania pierwiastkowego (niewiadoma występuje pod znakiem
pierwiastka). Technika rozwiązywania tego typu równań polega na takim jego przekształceniu, aby zlikwidować pierwiastki. Zwykle robimy to podnosząc obie strony równania do
kwadratu (raz lub więcej razy). Operacja podnoszenia do kwadratu może spowodować
wprowadzenie obcych pierwiastków, stąd rozwiązania powinny być sprawdzone. W przykładzie mamy:
( 10 x + 6 )2 = (9 − x)2 ⇔
x + 10 x + 6 = 9 ⇔ 10 x + 6 = 9 − x ⇔
⇔ 10 x + 6 = 81 − 18 x + x 2 ⇔ x 2 − 28 x + 75 = 0
∆ = (−28) 2 − 4 ⋅ 1 ⋅ 75 = 784 − 300 = 484 ,
x1 =
−(−28) − 22
2 ⋅1
=
28 − 22
2
= 3,
x2 =
∆ = 484 = 22 ,
−(−28) + 22
2 ⋅1
=
28 + 22
2
= 25 .
Sprawdzenie pierwiastków
Dla x1 = 3 mamy L = 3 + 30 + 6 = 3 + 36 = 3 + 6 = 9 , P = 9, L = P .
Dla x2 = 25 mamy L = 25 + 250 + 6 = 25 + 256 = 25 + 16 = 41, P = 9, L ≠ P .
Ostatecznie pierwiastkiem równania x + 10 x + 6 = 9 jest x = 3 .
Przykład 49. Rozwiązać równanie
1− x − x =
1
3
.
Podnosimy dwukrotnie do kwadratu obie strony tego równania otrzymując:
1 2
1
 ⇔ 1− x − 2 x 1− x + x = ⇔
3
 3
1
1
⇒ −2 x 1 − x = − 1 ⇔ x 1 − x = ⇔
3
3
( 1 − x − x )2 = 
⇒
(
x 1− x
)2 =  1 
 3
2
⇔ 9x − 9x + 1 = 0
2
⇔ x(1 − x) =
∆ = (−9) 2 − 4 ⋅ 9 ⋅ 1 = 81 − 36 = 45,
1
9
⋅ 9 ⇔ 9x − 9x2 − 1 = 0 ⇔
∆ = 45 = 3 5 ,
45
x1 =
− (−9) − 3 5 9 − 3 5 1
5
=
= −
2 ⋅9
18
2 6
x2 =
− (−9) + 3 5 9 + 3 5 1
5
=
= +
2⋅9
18
2 6
Sprawdzenie pierwiastków
1
5
−
mamy:
2 6
Dla x1 =
1
L = 1−
2
5
+
1
−
6
2
5
−
6
1
=
2
+
5
[(
]
)
[
Dla x2 =
5
−
[(
(
6+2 5
=
6
2
6
2
1 
 1+ 5 −
4⋅3 
1 
6+2 5 − 6−2 5 =

12 
1
1
1+ 5 − 1− 5 =
=
1+ 5 −
2 3
2 3
1
2
1
=
1+ 5 +1− 5 =
=
=P
2 3
2 3
3
=
1
−
)
12
−
6−2 5
12
(1 − 5 )2  =

)]
) (
5 −1 =
]
1
2
L = 1−
5
+
1
2
mamy:
6
−
6
−
1
2
+
(
[(
−
6+2 5
5
6
1
=
2
−
5
6
1
−
2
+
5
6
=
1 
6−2 5 − 6+2 5 =

12
12
2 3 
2
2
1 
1
=
1− 5 − 1+ 5 =
 1 − 5 − 1 + 5  ==
2 3
2 3

1
1
=
− 1 − 5 − 1 + 5 ==
−1+ 5 −1− 5 =
2 3
2 3
−2
−1
1
=
=
≠
=P
2 3
3
3
=
6−2 5
5
)
) (
=
(
[
)
)]
Ostatecznie pierwiastkiem równania
]
(
1− x − x =
)
1
3
jest x =
1
5
−
.
2 6
=
46
Przykład 50. Rozwiązać nierówność
1
2
x + 5x + 4
<0.
Powyższa nierówność będzie spełniona wtedy, gdy mianownik będzie przyjmował
wartości ujemne:
1
x2
+ 5x + 4
< 0 ⇔ x 2 + 5x + 4 < 0 .
Tę ostatnią nierówność rozwiążemy graficznie, ale wcześniej musimy znaleźć miejsca
zerowe trójmianu:
∆ = 52 − 4 ⋅1⋅ 4 = 25 − 16 = 9
y = x 2 + 5x + 4
∆ = 9 =3
x1 =
−5 − 3
= −4 ,
2
−5 + 3
x2 =
= −1 .
2
Z wykresu odczytujemy, że rozwiązaniem
nierówności x 2 + 5 x + 4 < 0 są −4 < x < −1 .
+
+
−4
−
−1
47
Zadania do samodzielnego rozwiązania
Odp. x1 = 0,
x 2 = 1,5 .
Odp. x1 = −8,
1
2
+
=1.
2x −1 2x + 1
x +8
24
−2 =
.
x −8
x−4
x 2 = 12 .
34. Znaleźć równanie kwadratowe x 2 + px + q = 0 , którego pierwiastki są odpowiednio
równe –9 i 8.
Odp. x 2 + x − 72 = 0 .
35. Dla jakiej wartości parametru k równanie (k + 2) x 2 + 6kx + 4k − 1 = 0
ma pierwiastek podwójny?
Odp. Dla k = 0,4 lub k = 1 .
36. Rozwiązać równanie x 4 + 2 x 2 + 1 = 0 .
Odp. Równanie sprzeczne.
37. Rozwiązać równanie 3 − x − 1 = 3x − 2 .
Odp. x = 2 .
Odp. x < −3 lub x ≥
2x −1
≥ 0.
x+3
1
.
2
x2 + 4
<0.
x2 − x − 6
Odp. −2 < x < 3 .
40. Dla jakiej wartości parametru m nierówność mx 2 + x + 5m − 2 > 0 jest spełniona
dla wszystkich x ∈ R ?
Odp. m > 0,5 .
48
41. Dla jakiej wartości parametru m równanie mx 2 + 3 x − m + 5 = 0 ma dwa różne
pierwiastki?
Odp. Dla m < 0 lub 0 < m <
1
2
lub m >
9
2
.
42. Dla jakiej wartości parametru m równanie mx 2 + 3 x − m + 5 = 0 ma dwa różne
pierwiastki dodatnie?
Odp. Dla 0 < m <
1
2
lub
9
2
< m < 5.
43. Dla jakiej wartości parametru m pierwiastki równania
1
1
mx
m +1
+
< 2m + 1 .
+
= x + 1 spełniają nierówność
x1 x 2
m −1
x
Odp. Dla −1,5 < m < −1 lub 0 < m < 1 .
49
3. Rozwiązania zadań
Zadanie 1. Rozłożyć na czynniki wyrażenie a 5 − a 3 + a 2 − 1 :
a 5 − a 3 + a 2 − 1 = a 3 a 2 − a 3 + a 2 − 1 = a 3 (a 2 − 1) + (a 2 − 1) =
= (a 2 − 1)(a 3 + 1) = (a − 1)(a + 1)(a + 1)(a 2 − a + 1) = (a − 1)(a + 1) 2 (a 2 − a + 1)
Zadanie 2. Rozłożyć na czynniki wyrażenie bc(b + c) + ca (c − a ) − ab(a + b) :
bc(b + c) + ca(c − a ) − ab( a + b) = b 2c + bc 2 + ac 2 − a 2c − ab(a + b) =
= b 2c − a 2c + bc 2 + ac 2 − ab( a + b) = c(b 2 − a 2 ) + c 2 (b + a ) − ab( a + b) =
[
]
= c(b − a )(b + a ) + c 2 (b + a ) − ab( a + b) = (a + b) c(b − a ) + c 2 − ab =
= ( a + b)(cb − ac + c 2 − ab) = (a + b)(b(c − a ) + c(c − a )) =
= ( a + b)(c − a)(b + c)
Zadanie 3. Uprościć wyrażenie
x 2 + 1x
x + 1x − 1
:
x3 + 1
x +
x3 + 1
x
x3 + 1
x
=
=
⋅
=
=
x + 1x − 1 x 2 + 1 − x
x
x2 − x + 1 x2 − x + 1
x
2
=
1
x
( x + 1)( x 2 − x + 1)
x2 − x + 1
= x +1
2
2
 ab
 a − b a + b  a + b
Zadanie 4. Uprościć wyrażenie 
+
+ 1 2
:

 a + b2
 a + b a − b  2ab

 a − b a + b  a 2 + b 2  ab
+
+1 2 2 =


 a +b
 a + b a − b  2ab

=
=
( a − b) 2 + (a + b) 2 a 2 + b 2 + 2ab
ab
⋅
⋅ 2 2 =
2ab
a2 − b2
a +b
ab(a 2 − 2ab + b 2 + a 2 + 2ab + b 2 )(a + b) 2
2
2
2
2
2ab( a + b )( a − b )
=
2(a 2 + b 2 )(a + b)
2
2
2(a + b )(a − b)
=
a+b
a −b
50
 1
1 1
1 
2

 + :
+ 2  +
2
3

( x + y)  x
y  ( x + y )  x y 
1
2
 1
1 1
1
1 
2

 + =
+ 2  +
2 2
( x + y)  x
y  ( x + y ) 3  x y 
 y 2 + x 2 
1
2  y + x 

 =
=
 2 2  +
2 
(x + y )  x y  x + y  xy 
=
=
1
2
xy (x + y )
 x2 + y2

 x 2 + y 2 + 2 xy 
1

=
+ 2 =

2

xy
 xy ( x + y ) 
 xy

(x + y )2
x 2 y 2 (x + y )2
=
1
x y
2 2


1+ a
1− a
1
1


+
−  dla 0 < a < 1 :
 a2 −1 a 
 1+ a − 1− a

2
1 − a − 1 + a 



 1
1+ a
1− a
1


+
−1 −  =
 a2
 1+ a − 1− a

2
a 
1 − a − 1 + a 


 1 − a 2 1 
1+ a
1− a

−
=
=
+
 1+ a − 1− a
a
a2
(1 − a )(1 + a) − (1 − a ) 



 1
1+ a
1− a 1− a
 ⋅  1 − a 2 − 1 =
=
+
 1+ a − 1− a
 a

a
a
a
1
−
1
+
−
1
−


(

1+ a
1− a
=
+
 1+ a − 1− a
a
1
+
− 1− a

)
1
  1 − a 2 − 1 =
a


1+ a + 1− a 1 
1+ a + 1− a 1+ a − 1− a 1 
⋅  1 − a 2 − 1 =
⋅
⋅  1 − a 2 − 1 =



a
1+ a − 1− a
1+ a − 1− a 1+ a − 1− a a 
(1 + a) − (1 − a ) 1 
2a
1
=
⋅  1 − a 2 − 1 =
⋅  1 − a 2 − 1 =
2
 1 + a − 2 1 − a2 + 1 − a a 

a
1+ a − 1− a
=
(
)
2a 1 − a 2 − 1
1

 = −1
2

=
⋅  1 − a − 1 =
 − 2a 1 − a 2 − 1
2 − 2 1 − a2 a 




2a
51
 4 a 3 − 4 b3
 a

Zadanie 7. Uprościć wyrażenie 
− 4 a − 4 b  4 + 1 :


 b

a− b


 4 3 4 3 
 4 a3 − 4 b3

   a − b 

4
4 4 a

− a− b
+1 = 
−
 
 a− b
 b
a− b

 



 4 3 4 3  4
4
 a − b − a + b


=

a− b


(
(
4

 4 a + 4 b 
=
a + b 
  4 b 


4
)

a − b  4
4

 a + b  =

4

b 


)(
)
 4 3 4 3  4 3 4 2 4 2
4 3 
  a − b  −  a − ab + a b − b    4
4



   a + b 
=
=

  4 b 
a− b




4
2


4
b  4 ab − a  4
 4 ab 2 − 4 a 2 b   4 a + 4 b 
4

 a+ b

=
=
⋅
=
4

a − b   4 b 
a− b
b

4
=
a
( b − a )(
4
4
4
a +4b
) == a ( b − a ) = − a (
4
4
a− b
a− b
a − 2 a +1
a − 2 a +1
4
a − 2 a +1
:
4
4
a +1
a −1
a −1
=
(
4
)(
a −1
Wyrażenie
4
)
4
a − 2 a +1
4
:4
2
+1 =
+1 =
a +1
( a − 1)
(
)
4
a −1
a −1
2
( a)
4
2
− 12
⋅
a− b
a +1
a −1
4
a −1
4
a +1
+1 =
a− b
+1:
+1 =
a −1
a −1
+1
 a − 1 dla a > 1
, stąd
a −1 = 
− a + 1 dla 0 < a < 1
 a −1
+1 = 1+1 = 2
dla a > 1


+1 =  a −1
a −1
 − a − 1 + 1 = −1 + 1 = 0 dla 0 < a < 1
 a − 1
a −1
(
)
)= −
4
a
52
1
Zadanie 9. Usunąć niewymierność z mianownika
.
2+ 2 +3 4
Przy rozwiązywaniu tego zadania będziemy musieli skorzystać z następujących
związków:
a 3 − b3
a 3 − b3 = (a − b)(a 2 + ab + b 2 ) ⇒ a 2 + ab + b 2 =
a−b
oraz
3
a 3 + b3
,
a+b
a 3 + b3 = (a + b)(a 2 − ab + b 2 ) ⇒ a 2 − ab + b 2 =
przy czym wykorzystanie tych wzorów będzie poprzedzone pewnymi przygotowaniami.
1
3
2+ 2 + 4
=
1
=
3
2
( 2)
+ 2⋅ 2+
1
3
( 2) − ( 2)
+ 3 2 − 2 ⋅3 2
(
)(
2 −3 2
=
=
− 2 ⋅3 2 + 3 2
1
(
3
2 2 −2+
2 − 2 ⋅3 2
)(
2 −3 2
)=
2 −3 2
2 −3 2
2 2 − 2 + 3 2 1− 2
2
( 2)
3
=
3
3
2 −3 2
=
3
2 −3 2
2 −3 2
=
) 2(
)
2 −1 − 3 2
(
)(
2 −1
2 −3 2
=
⋅
2 −3 2
2 +1
)=
=
( 2 − 1)[2 − 2 ( 2 − 2 )] ( 2 − 1)[2 − 2 ( 2 − 2 )] 2 + 1
( 2 − 2 )( 2 + 1) = ( 2 − 2 )( 2 + 1) = ( 2 − 2 )( 2 + 1) =
=
[2 − 2 ( 2 − 2 )] 2 − 2 2 + 4 ( 2 ) − 2 2 + ( 2 )
( 2 − 2 )( 2 + 1) = ( 2 − 2 )( 2 + 1)( 2 + 2 ) = (2 − 4 )( 2 + 1) =
=
2 2+2
2( 2 + 1)
( 2) + ( 2)
3
3
3
3
3
3
3
3
3
3
3
3
2
3
3
3
3
2
3
3
3
3
2 +3 2
2−3 4
= 1 − 12 3 4 .
2
Inne (szybsze) rozwiązanie tego samego zadania:
=
1
2+3 4 +3 2
=
=
2−3 4
= 1−
2(2 − 1)
3
1
3
2
13
2
(
3
4.
)
4 + 3 2 +1
=
3
23 4
(
3
4
(
3
)
2 −1
)(
2 −1
3
)
4 + 3 2 +1
=
2−3 4
2  3 2

3
( )
3
−1 

=
53
Zadanie 10. Usunąć niewymierność z mianownika
1
dla a ≥ b > 0 :
2
a+ a −b
2
1
a + a2 − b2
=
a + a2 − b2
=
a + a2 − b2 ⋅ a + a2 − b2
a + a2 − b2
a + a2 − b2
a + a2 − b2
=
 a + a2 − b2 




a − a2 − b2
⋅
 a + a2 − b2  a − a2 − b2




 a − a2 − b2  a + a2 − b2



=
=
2
a − (a 2 − b 2 )
(a
=
2
2
a − a2 − b2   a + a2 − b2 

 


 

=
2
b
− (a 2 − b 2 )  a − a 2 − b 2 


=
2
b
b 2  a − a 2 − b 2 


=
2
b
)
b a − a2 − b2
b2
=
a − a2 − b2
.
b
Inne (szybsze) rozwiązanie tego samego zadania:
1
a + a2 − b2
=
=
a − a2 − b2
=
(a +
=
a + a 2 − b2 ⋅ a − a 2 − b2
a − a 2 − b2
)(
a2 − b2 a − a2 − b2
a − a2 − b2
a 2 − (a 2 − b 2 )
=
)
=
a − a2 − b2
b2
2
=
 a − a 2 − b 2  a + a 2 − b 2  a − a 2 − b 2 








=
2
b
=
=
a + a2 − b2
=
=
a − a 2 − b2
b
=
54
Zadanie 11. Usunąć niewymierność z mianownika:
1
=
10 − 15 + 14 − 21
1
5
(
)
2 ⋅5 − 3⋅5 + 2 ⋅ 7 − 3⋅ 7
1
=
2− 3
2− 3 5+ 7
=
=
(
) (
)(
)
( 2 + 3 )( 5 − 7 )
( 2 + 3 )( 5 − 7 ) =
=
(2 − 3)(5 − 7)
3 )( 5 + 7 )( 2 + 3 )( 5 − 7 )
3 )( 5 − 7 )
2− 3 + 7
=
(
(
=
1
=
2−
2+
2
Zadanie 12. Rozwiązać równanie
1
2
(3 − 2 y )
1
2
−
3
9 − 4y
2
=
2
(3 − 2 y )
−
3
9 − 4y
(
=
4
(3 + 2 y )2
=
4
⋅ (3 − 2 y )2 (3 + 2 y )2
) (
9 + 12 y + 4 y 2 − 3 9 − 4 y 2 = 4 9 − 12 y + 4 y 2
2
9 + 12 y + 4 y − 27 + 12 y = 36 − 48 y + 16 y
)
2
12 y + 16 y 2 + 48 y − 16 y 2 = 36 − 9 + 27
60 y = 54
9
y=
= 0,9.
10
Zadanie 13. Rozwiązać równanie ( x + 2)( x − 3) = ( x − 5)( x − 6) :
( x + 2)( x − 3) = ( x − 5)( x − 6)
x 2 − 3 x + 2 x − 6 = x 2 − 6 x − 5 x + 30
− x + 11x = 30 + 6
10 x = 36
x = 3,6.
:
(3 + 2 y )2
(3 − 2 y ) (3 − 2 y )(3 + 2 y ) (3 + 2 y )2
(3 + 2 y )2 − 3(3 + 2 y )(3 − 2 y ) = 4(3 − 2 y )2
2
2
4
3
−
1
55
3− x
1
+
= 2:
x−2 2− x
3− x
1
+
=2
x−2 2− x
x−3
1
+
= 2 ⋅ (2 − x ) dla x ≠ 2
2− x 2− x
x − 3 + 1 = 2( 2 − x )
x + 2 x = 4 + 2 ⇔ 3x = 6 ⇔ x = 2 .
Dla x = 2 jednak wyrażenie po lewej stronie znaku równości nie ma sensu, ponieważ
wymaga niewykonalnego działania, jakim jest dzielenie przez zero. Wobec tego równanie
nie ma żadnych rozwiązań, czyli jest sprzeczne.
3
3
2
x −1
−
2x
5x
2x
= 2
−
:
x + 1 x −1 x −1
2x
5x
2x
= 2
−
⋅ ( x − 1)( x + 1)
x
+
1
x
−1
x −1
x −1
3 − 2 x( x − 1) = 5 x − 2 x( x + 1)
2
−
3 − 2x 2 + 2x = 5x − 2x 2 − 2x
2 x − 5 x + 2 x = −3
− x = −3
x = 3.
Zadanie 16. Masa wodoru zawartego w wodzie stanowi 12,5% masy zawartego w niej
tlenu. Ile kg wodoru i ile kg tlenu znajduje się w 8,1 kg wody?
Oznaczmy masę tlenu w wodzie symbolem x. Z treści zadania wynika, że masa wodoru
w wodzie jest równa 12,5% x . Tym samym łączna masa tlenu i wodoru w wodzie jest
równa x + 0,125 x = 1,125 x . Ponieważ 1,125 x = 8,1 , więc
x=
8,1
1,125
=
81 9 81 8 72
: = ⋅ =
= 7, 2 .
10 8 10 9 10
W 8,1 kg wody mamy więc 7,2 kg tlenu i 0,9 kg wodoru.
56
Zadanie 17. Ile gramów stopu 30% i ile gramów stopu 70% należy zmieszać, aby otrzymać
500 gramów stopu 60%?
Oznaczmy ilość stopu 30% symbolem x, tym samym musimy wziąć 500 − x gramów
stopu 70%. Można już zapisać równanie określające stop 60%:
x ⋅ 30% + (500 − x) ⋅ 70% = 500 ⋅ 60% .
Rozwiązanie tego równania daje ilość gramów obu stopów niezbędną do otrzymania
stopu 60%:
0,3x + 0,7(500 − x) = 0,6 ⋅ 500
0,3x + 0,7(500 − x) = 300
0,3x + 350 − 0,7 x = 300
− 0,4 x = −50
x=
− 50
= 125.
− 0,4
Aby otrzymać 500 gramów 60% stopu, trzeba zmieszać 125 gramów stopu 30% i 375
gramów stopu 70%.
Zadanie 18. Rozwiązać nierówność 4 x − 3 < x + 6 :
4x − 3 < x + 6
4x − x < 6 + 3
3x < 9 : 3
x < 3.
Zadanie 19. Rozwiązać nierówność
4x + 1 x + 4
>
⋅ 10
2
5
5(4 x + 1) > 2( x + 4)
20 x + 5 > 2 x + 8
18 x > 3 : 18
x>
1
.
6
4x + 1 x + 4
>
:
2
5
57
Zadanie 20. Rozwiązać nierówność ( x + 5)(4 − x) > 0 .
Iloczyn wyrażeń ( x + 5)(4 − x ) jest większy od 0 wtedy i tylko wtedy, gdy oba
wyrażenia są tych samych znaków. Otrzymujemy stąd dwa układy nierówności:
x + 5 < 0
x + 5 > 0
lub 

4 − x < 0
4 − x > 0
Rozwiązując te układy otrzymujemy:
 x + 5 < 0  x < −5
 x < −5
⇒
⇒
- układ sprzeczny,

−
x
<
−
4
⋅
(
−
1
)
x>4
4 − x < 0 
 x + 5 > 0  x > −5
 x > −5
⇒
⇒
, czyli −5 < x < 4 .

−
x
>
−
4
⋅
(
−
1
)
4
−
x
>
0
x<4


Ostatecznie rozwiązaniem naszej nierówności są x : −5 < x < 4 .
Zadanie 21. Rozwiązać nierówność (3 x − 1) 2 + (4 x − 1) 2 < (5 x − 1) 2 :
(3 x − 1) 2 + (4 x − 1) 2 < (5 x − 1) 2
9 x 2 − 6 x + 1 + 16 x 2 − 8 x + 1 < 25 x 2 − 10 x + 1
− 14 x + 10 x < 1 − 2
− 4 x < −1
x > 0,25.
3x − 15 < 0
3x − 15
<0⇔
x−2
 x−2 > 0
3x − 15
< 0:
x−2
∨
3x − 15 > 0

 x−2 < 0
3x − 15 < 0  x − 5 < 0  x < 5
⇒
⇒
⇒2<x<5

 x−2 > 0
x − 2 > 0 x > 2
3 x − 15 > 0  x − 5 > 0  x > 5
⇒
⇒
- układ sprzeczny.

 x−2 < 0
x − 2 < 0 x < 2
Ostatecznie rozwiązaniem nierówności
3x − 15
< 0 są x : 2 < x < 5 .
x−2
58
2x +1
>1:
x+2
2x +1
>1
x+2
2x +1
−1 > 0
x+2
2 x + 1 − ( x + 2)
>0
x+2
2x +1− x − 2
>0
x+2
 x −1 > 0
 x −1 < 0
x −1
>0⇔
∨ 
x
+
2
>
0
x+2

x + 2 < 0
 x −1 > 0
 x >1
⇔
⇔ x >1

+
>
x
2
0

 x > −2
 x −1 < 0
 x <1
⇔
⇔ x < −2 .

x + 2 < 0
 x < −2
Ostatecznie rozwiązaniem układu nierówności są x < −2 lub x > 1 .
 x − 5y = 1
Zadanie 24. Rozwiązać układ równań 
:
x + 2 y = 2
dodajemy stronami
1
 x − 5 y = 1 ⋅ (−1)
− x + 5 y = −1
⇔
7y =1 ⇔ y = .

⇒
x
+
2
y
=
2
x
+
2
y
=
2
7


Np. z drugiego równania wyznaczamy x:
x + 2⋅
1
7
= 2 ⇔ 7 x + 2 = 14 ⇔ 7 x = 12 ⇔ x =
12
7
.
Ostatecznie rozwiązaniem tego układu równań jest x = 127 i y =
 2x − y = 3 + x
Zadanie 25. Rozwiązać układ równań 
:
 x − 0,5 y = 3 + 0,5 x
x − y = 3
2 x − y = 3 + x
x − y = 3
⇔
⇔

 x − 0,5 y = 3 + 0,5 x
x − y = 6
0,5 x − 0,5 y = 3 ⋅ 2
Otrzymany układ równań nie posiada rozwiązań, jest sprzeczny.
1
7
.
59
Zadanie 26. Po zmieszaniu dwóch roztworów kwasu solnego 75% i 54% otrzymano 42
litry roztworu 66%. Jakie ilości roztworów o stężeniu 75% i 54% zmieszano?
Oznaczając przez x ilość kwasu 75%, a przez y ilość kwasu 54% możemy utworzyć
następujący układ równań:
 x + y = 42

0,75 x + 0,54 y = 0,66 ⋅ 42
 x + y = 42
 x + y = 42
⇔

0,75 x + 0,54 y = 0,66 ⋅ 42
0,75 x + 0,54 y = 27,72
Z pierwszego równania mamy x = 42 − y , a po podstawieniu do drugiego równania
otrzymujemy:
0,75(42 − y ) + 0,54 y = 27,72
31,5 − 0,75 y + 0,54 y = 27,72
− 0,21 y = −3,78
y = 18.
W takim razie x = 42 − 18 = 24 . Ostatecznie trzeba wziąć odpowiednio 24 i 18 kg
kwasu o stężeniu 75% i 54% w celu otrzymania 42 litrów kwasu o stężeniu 66%.
Zadanie 27. W prostokątnym układzie współrzędnych X0Y na płaszczyźnie wyznaczyć
punkty, których współrzędne spełniają układ nierówności
y < 3
, czyli po przekształceniu

 y − 6 > −2 x
y < 3
y < 3
⇔

 y − 6 > −2 x
 y > −2 x + 6
Po wykreśleniu obu prostych zaznaczamy punkty o współrzędnych spełniających
obie nierówności (obszar zakreskowany, bez półprostych tworzących brzeg tego obszaru).
l1 : y = 3
l2 : y = − 2 x + 6
60
Zadanie 28. W prostokątnym układzie współrzędnych X0Y na płaszczyźnie wyznaczyć
y < 3

 y − 6 > −2 x
x ≤ 5

Zadanie to rozwiązujemy analogicznie do poprzedniego, jedyna różnica wynika z faktu,
że pojawia się jeszcze jedna prosta.
l2 : y = −2 x + 6
l3 : x = 5
l1 : y = 3
Współrzędne punktów należących do prostych narysowanych linią przerywaną nie
spełniają podanego układu nierówności.
Zadanie 29. W prostokątnym układzie współrzędnych X0Y na płaszczyźnie zaznaczyć
 2x + y − 2 ≤ 0
4 x + 2 y + 1 > 0

Przekształcamy ten układ nierówności w podobny sposób jak układ z poprzedniego
przykładu:
 y ≤ −2 x + 2
 2x + y − 2 ≤ 0
 y ≤ −2 x + 2
4 x + 2 y + 1 > 0 ⇔ 2 y > −4 x − 1 : 2 ⇔  y > −2 x − 0,5



61
l 2 : y = −2 x − 0,5
l1 : y = −2 x + 2
Zwróćmy uwagę, że w obu równaniach prostych: y = −2 x + 2 i y = −2 x − 0,5
występuje ten sam współczynnik przy x, czyli współczynnik kierunkowy, równy −2 .
Proste o takim samym współczynniku kierunkowym są do siebie równoległe (gdyby
jeszcze wyrazy wolne były takie same, to proste te byłyby sobie równe, czyli nakładałyby
się na siebie). Wobec tego graficznym rozwiązaniem nierówności jest zbiór wszystkich
punktów płaszczyzny położonych w pasie nieskończonym ograniczonym dwiema prostymi
równoległymi, przy czym punkty prostej y = −2 x + 2 należą do tego zbioru (ze względu na
nieostrą nierówność y ≤ −2 x + 2 ), natomiast punkty prostej y = −2 x − 0,5 nie należą do
tego zbioru (ze względu na ostrą nierówność y > −2 x − 0,5 ). Z tego powodu na rysunku
prosta y = −2 x + 2 zaznaczona jest linią ciągłą, a prosta y = −2 x − 0,5 - linią przerywaną.
Uwaga. Gdybyśmy zamiast układu nierówności
 2x + y − 2 ≤ 0
4 x + 2 y + 1 > 0

rozwiązywali układ równań
 2x + y − 2 = 0
4 x + 2 y + 1 = 0 ,

stwierdzilibyśmy, że układ jest sprzeczny, czyli nie ma rozwiązania. Powyższe wyjaśnienia
tłumaczą przyczynę takiego stanu rzeczy: dwie proste równoległe nie mają żadnego punktu
wspólnego.
 2x + y − 2 > 0
4 x + 2 y + 1 < 0

62
Wyrażenia występujące w nierównościach są takie same jak w poprzednim przykładzie,
inne są teraz jednak znaki obu nierówności. Rozwiązanie:
 y > −2 x + 2
 2x + y − 2 > 0
 y > −2 x + 2
4 x + 2 y + 1 < 0 ⇔ 2 y < −4 x − 1 : 2 ⇔  y < −2 x − 0,5



l 2 : y = −2 x − 0,5
l1 : y = −2 x + 2
Graficznym rozwiązaniem nierówności y > −2 x + 2 jest zbiór wszystkich punktów
płaszczyzny położonych nad prostą y = −2 x + 2 , a rozwiązaniem nierówności
y < −2 x − 0,5 jest zbiór punktów położonych pod prostą y = −2 x − 0,5 . Widać, że oba
zbiory nie mają żadnego punktu wspólnego, co oznacza, że układ nierówności nie ma
rozwiązań (jest sprzeczny).
2 x + y − 2 > 0
x > 3

Rozwiązanie:
2 x + y − 2 > 0
 y > −2 x + 2
⇔
x > 3

x > 3
Aby narysować zbiór rozwiązań nierówności x > 3 , trzeba najpierw narysować prostą
x = 3 . Równanie tej prostej jest postaci x = c (a nie, jak dotychczas, y = ax + b ). Prosta
postaci x = c jest prostopadła do osi x-ów i przechodzi przez punkt c na tej osi. Graficznym
rozwiązaniem nierówności x > c ( x < c ) jest zbiór punktów płaszczyzny położonych na
prawo (na lewo) od prostej x = c .
63
l2 : x = 3
l1 : y = −2 x + 2
1
2
+
=1:
2x −1 2x + 1
1
2
+
= 1 ⋅ (2 x − 1)(2 x + 1)
2x − 1 2x + 1
2 x + 1 + 2(2 x − 1) = (2 x − 1)(2 x + 1)
2x + 1 + 4x − 2 = 4x 2 − 1
4 x 2 − 6 x = 0 ⇔ 4 x( x − 1,5) = 0 ⇔ x = 0 ∨ x = 1,5.
x+8
−2=
x +8
24
−2 =
:
x −8
x−4
24
⋅ ( x − 8)( x − 4)
x −8
x−4
( x + 8)( x − 4) − 2( x − 8)( x − 4) = 24( x − 8)
x 2 − 4 x + 8 x − 32 − 2 x 2 + 24 x − 64 = 24 x − 192
x 2 − 4 x − 96 = 0
∆ = (−4) 2 − 4 ⋅ 1 ⋅ (−96) = 16 + 384 = 400,
Ostatecznie rozwiązaniami równania
x1 =
−(−4) − 20
2 ⋅1
= −8,
x2 =
∆ = 400 = 20 .
x +8
24
−2 =
są pierwiastki:
x −8
x−4
−(−4) + 20
2 ⋅1
Zadanie 34. Znaleźć równanie kwadratowe
odpowiednio równe –9 i 8.
= 12 .
x 2 + px + q = 0 , którego pierwiastki są
64
Korzystając ze wzoru na postać iloczynową mamy:
x 2 + px + q = 0 ⇔ ( x − x1 )( x − x 2 ) = 0 ⇔ ( x + 9)( x − 8) = 0 ⇔
⇔ x 2 − 8 x + 9 x − 72 = 0 ⇔ x 2 + x − 72 = 0.
Zadanie 35. Dla jakiej wartości parametru k równanie (k + 2) x 2 + 6kx + 4k − 1 = 0
ma pierwiastek podwójny?
Wtedy, gdy ∆ = 0 , czyli 36k 2 − 4(k + 2)(4k − 1) = 0 . Mamy
36k 2 − 4(k + 2)(4k − 1) = 0 ⇔ 9k 2 − (k + 2)(4k − 1) = 0 ⇔
⇔ 9k 2 − 4k 2 + k − 8k + 2 = 0 ⇔ 5k 2 − 7k + 2 = 0
∆ = (−7) 2 − 4 ⋅ 5 ⋅ 2 = 49 − 40 = 9,
k1 =
− ( −7 ) − 3
= 0,4,
2⋅5
k2 =
∆ = 9 =3
− ( −7 ) + 3
=1.
2⋅5
Ostatecznie równanie (k + 2) x 2 + 6kx + 4k − 1 = 0 ma pierwiastek podwójny dla k = 0,4
lub k = 1 .
Zadanie 36. Rozwiązać równanie x 4 + 2 x 2 + 1 = 0 .
Podstawiając x 2 = z sprowadzamy równanie dwukwadratowe do kwadratowego:
x4 + 2x2 + 1 = 0 ⇒ z 2 + 2z + 1 = 0
∆ = 2 2 − 4 ⋅ 1 ⋅ 1 = 4 − 4 = 0,
∆ = 0 = 0,
z1 = z 2 =
−2
= −1 .
2
Ponieważ równanie x 2 = −1 jest sprzeczne (nie ma rozwiązania), więc również
równanie x 4 + 2 x 2 + 1 = 0 jest sprzeczne.
Zadanie 37. Rozwiązać równanie 3 − x − 1 = 3x − 2 :
(
3 − x − 1 = 3x − 2 ⇔ 3 − x − 1
2
2
) = ( 3x − 2 )
⇔
⇔ 9 − 6 x − 1 + x − 1 = 3 x − 2 ⇔ 10 − 2 x = 6 x − 1 ⇔ 5 − x = 3 x − 1 ⇔
(
2
)
⇔ (5 − x )2 = 3 x − 1 ⇔ 25 − 10 x + x 2 = 9 x − 9 ⇔ x 2 − 19 x + 34 = 0
65
∆ = (−19) 2 − 4 ⋅ 1 ⋅ 34 = 361 − 136 = 225,
x1 =
− (−19) − 15
= 2,
2
x2 =
∆ = 225 = 15
− (−19) + 15
= 17.
2
Sprawdzenie rozwiązań
Dla x = x1 = 2 mamy:
L = 3 − 2 −1 = 3 − 1 = 3 −1 = 2
P = 3⋅ 2 − 2 = 4 = 2
L = P.
Dla x = x2 = 17
L = 3 − 17 − 1 = 3 − 16 = 3 − 4 = −1
P = 3 ⋅ 17 − 2 = 51 − 2 = 49 = 7
L ≠ P.
Ostatecznie rozwiązaniem równania pierwiastkowego 3 − x − 1 = 3x − 2 jest x = 2 .
2x −1
≥ 0.
x+3
Z uwagi na nierówność słabą powyższa nierówność nie jest równoważna nierówności
(2 x − 1)( x + 3) ≥ 0 . Poprawne rozwiązanie jest następujące:
2x − 1
2x − 1
1
 2x − 1



≥0⇔
=0 ∨
> 0 ⇔  x =
∨ (2 x − 1)( x + 3) > 0 ⇔
x+3
x+3
2
 x+3



1
1
1


⇔ x =
∨ x < −3 ∨ x >  ⇔ x < −3 ∨ x ≥ .
2
2
2

Ostatecznie rozwiązaniem nierówności
1
2x −1
≥ 0 są x < −3 lub x ≥ .
2
x+3
x2 + 4
<0.
x − x−6
2
x2 + 4
< 0 wtedy i tylko wtedy, gdy trójmian kwadratowy w mianox2 − x − 6
wniku będzie mniejszy od zera. Wynika to z faktu, że trójmian kwadratowy w liczniku jest
większy od zera dla dowolnych x-ów. Stąd:
Wyrażenie
66
x2 + 4
< 0 ⇔ x2 − x − 6 < 0
x − x−6
2
∆ = (−1) 2 − 4 ⋅ 1 ⋅ (−6) = 1 + 24 = 25,
x1 =
−(−1) − 5
2 ⋅1
=
1− 5
2
= −2,
x2 =
∆ = 25 = 5
−(−1) + 5
2 ⋅1
=
1+ 5
2
=3
x 2 − x − 6 < 0 ⇔ ( x + 2)( x − 3) < 0 .
Do rozwiązania
y = ( x + 2)( x − 3) .
tej
nierówności
wykorzystamy
szkic
wykresu
funkcji
y = ( x + 2)( x − 3)
+
+
−2
−
3
Ostatecznie rozwiązaniem nierówności ( x + 2)( x − 3) < 0 są x : −2 < x < 3 .
Zadanie 40. Dla jakiej wartości parametru m nierówność mx 2 + x + 5m − 2 > 0 jest
spełniona dla wszystkich x ∈ R ?
Nierówność powyższa będzie spełniona dla
wszystkich x ze zbioru liczb rzeczywistych wtedy
i tylko wtedy, gdy wykres trójmianu kwadratowego
y = mx 2 + x + 5m − 2 będzie położony całkowicie
nad osią x-ów (rysunek obok). Stanie się tak wtedy,
gdy współczynnik stojący przy x w drugiej potędze
będzie większy od zera, a wyróżnik trójmianu będzie
ujemny. Warunki te można zapisać w postaci układu
nierówności:
m > 0
.

∆ = 1 − 4m(5m − 2) < 0
y = mx 2 + x + 5m − 2
dla m > 0 i ∆ < 0
+
+
+
67
Rozwiązując drugi z podanych warunków mamy kolejno:
1 − 4m(5m − 2) < 0 ⇔ 1 − 20m 2 + 8m < 0 ⇔ 20m 2 − 8m − 1 > 0 .
Trójmian po lewej stronie znaku nierówności sprowadzamy do postaci iloczynowej:
∆ = (−8) 2 − 4 ⋅ 20 ⋅ (−1) = 64 + 80 = 144 ,
∆ = 144 = 12, stąd m1 =
−(−8) − 12
4
−(−8) + 12
=−
= −0,1 oraz m2 =
= 0,5 .
2 ⋅ 20
40
40
Ostatecznie 20m 2 − 8m − 1 > 0 ⇔ 20(m + 0,1)(m − 0,5) > 0 ⇔ m < −0,1 ∨ m > 0,5 .
Z powyższego wynika, że wyróżnik trójmianu y = mx 2 + x + 5m − 2 jest ujemny dla
m < −0,1 lub m > 0,5 . Po połączeniu tego warunku z wymogiem, aby wykres trójmianu
położony był nad osią x-ów, mamy jako ostateczne rozwiązanie m > 0,5 .
Tym samym dla m > 0,5 nierówność mx 2 + x + 5m − 2 > 0
wszystkich x ∈ R .
jest spełniona dla
Zadanie 41. Dla jakiej wartości parametru m równanie mx 2 + 3 x − m + 5 = 0 ma dwa
różne pierwiastki?
Aby równanie kwadratowe ax 2 + bx + x = 0 miało dwa różne pierwiastki, musi być
spełniony warunek, że ∆ = b 2 − 4ac > 0 . W zadaniu mamy: a = m, b = 3, c = −m + 5 .
Wobec tego
∆ = 3 2 − 4 ⋅ m ⋅ (5 − m) = 4m 2 − 20m + 9 .
Musimy więc rozwiązać nierówność kwadratową 4m 2 − 20m + 9 > 0 . Zaczynamy od
wyznaczenia pierwiastków równania kwadratowego
kolejno:
∆ = (−20) 2 − 4 ⋅ 4 ⋅ 9 = 400 − 144 = 256,
m1 =
−(−20) − 16 4 1
= = ,
2⋅4
8 2
m2 =
4m 2 − 20m + 9 = 0 , otrzymując
∆ = 256 = 16 ,
−(−20) + 16 36 9
=
= .
2⋅4
8 2
Postępując podobnie jak w przykładzie 44 stwierdzamy, że rozwiązaniami nierówności
4m 2 − 20m + 9 > 0 są m < 12 lub m > 92 .
Nie jest to jednak ostateczna odpowiedź, ponieważ warunek ∆ > 0 ma sens tylko
w przypadku równania kwadratowego, inaczej mówiąc przyjęliśmy milcząco założenie, że
68
a = m ≠ 0 . Jeżeli m = 0, to równanie mx 2 + 3 x − m + 5 = 0 staje się równaniem liniowym
3x + 5 = 0 , które ma tylko jeden pierwiastek x = − 53 .
Ostatecznie więc równanie mx 2 + 3 x − m + 5 = 0 ma dwa różne pierwiastki dla m < 0
lub 0 < m <
1
2
lub m >
9
2
.
Zadanie 42. Dla jakiej wartości parametru m równanie mx 2 + 3 x − m + 5 = 0 ma dwa
różne pierwiastki dodatnie?
Zadanie to jest podobne do poprzedniego, z poprzedniego rozwiązania wynika, że dwa
różne pierwiastki równanie mx 2 + 3 x − m + 5 = 0 będzie miało wtedy, gdy m < 0 lub
0<m<
1
2
lub m >
9
2
.
Warunek powyższy musi być jednak uzupełniony o dodatkowe warunki gwarantujące,
że będą to pierwiastki dodatnie. Do ich sformułowania wykorzystamy wzory na sumę
i iloczyn pierwiastków trójmianu kwadratowego (wzory Viete’a):
x1 + x 2 = −
b
,
a
x1 ⋅ x 2 =
c
.
a
Konieczne są oba warunki, dopiero łączne ich sformułowanie gwarantuje to, że oba
pierwiastki będą dodatnie. Wykorzystanie tylko pierwszego z nich nie gwarantuje takiej
sytuacji, może być bowiem tak, że są różnych znaków, ale ich suma jest dodatnia. Z kolei
tylko drugi z nich nie wyklucza sytuacji, gdy oba są ujemne (ale ich iloczyn jest dodatni).
Stąd konieczność sformułowania i zbadania obu warunków. W zadaniu mamy:
x1 + x 2 = −
x1 ⋅ x 2 =
3
>0,
m
−m + 5
>0.
m
Pierwszy z tych warunków jest spełniony dla m > 0 . Rozwiązujemy drugi z warunków:
−m + 5
> 0 ⇔ −m(m − 5) > 0 ⇔ m(m − 5) < 0 ⇔ 0 < m < 5 .
m
Łącząc wszystkie trzy warunki otrzymujemy ostateczne rozwiązanie: równanie
mx 2 + 3 x − m + 5 = 0 będzie miało dwa różne pierwiastki dodatnie wtedy, gdy 0 < m < 12
lub
9
2
< m < 5.
69
Zadanie 43. Dla jakiej wartości parametru m pierwiastki równania
mx
m +1
+
= x +1
m −1
x
spełniają nierówność
1
1
+
< 2m + 1 .
x1 x 2
Z uwagi na postać równania musimy przyjąć założenie, że m ≠ 1 i x ≠ 0 . Przy tych
założeniach przekształcamy równanie wyjściowe do postaci ax 2 + bx + c = 0 . Mamy
kolejno:
mx
m +1
+
= x + 1 ⋅ x(m − 1)
m −1
x
mx ⋅ x + (m − 1) ⋅ (m + 1) = ( x + 1) ⋅ x ⋅ (m − 1)
mx 2 + m 2 − 1 = x(mx − x + m − 1)
mx 2 + m 2 − 1 = mx 2 − x 2 + mx − x
x 2 + (1 − m) x + m 2 − 1 = 0.
Równanie x 2 + (1 − m) x + m 2 − 1 = 0 będzie mieć dwa pierwiastki (niekoniecznie
różne) wtedy, gdy ∆ = b 2 − 4ac ≥ 0 .
W zadaniu mamy a = 1, b = 1 − m, c = m 2 − 1 , możemy więc warunek na nieujemną
deltę zapisać w postaci:
∆ = (1 − m) 2 − 4 ⋅ 1 ⋅ (m 2 − 1) ≥ 0 .
Porządkując lewą stronę otrzymujemy nierówność:
(1 − m) 2 − 4 ⋅ 1 ⋅ (m 2 − 1) ≥ 0 ⇔ 1 − 2m + m 2 − 4m 2 + 4 ≥ 0 ⇔ −3m 2 − 2m + 5 ≥ 0 .
Nierówność
− 3m 2 − 2m + 5 ≥ 0
rozwiązujemy analogicznie do wcześniejszych
przykładów, czyli znajdujemy miejsca zerowe trójmianu y = −3m 2 − 2m + 5 , szkicujemy
jego wykres i odczytujemy wartości m , dla których nierówność jest spełniona.
Kolejno mamy:
∆ = (−2) 2 − 4 ⋅ (−3) ⋅ 5 = 4 + 60 = 64,
∆ = 64 = 8
− (−2) − 8 − 6
− (−2) + 8 10
5
=
= 1,
m2 =
=
=− .
2 ⋅ (−3)
−6
2 ⋅ (−3)
−6
3
Możemy
już
sporządzić
szkic
wykresu
trójmianu
2
5
y = −3m − 2m + 5 = −3(m − 1)(m + 3 ) .
m1 =
kwadratowego
70
y = −3m 2 − 2m + 5 = −3(m − 1)(m + 53 )
+
−
+
− 53
1
−
Jak łatwo odczytać ze szkicu wykresu, nierówność − 3m 2 − 2m + 5 ≥ 0 spełniona jest
dla − 53 ≤ m ≤ 1 .
Uwzględniając założenie wyjściowe m ≠ 1 mamy, że równanie
mx
m +1
+
= x +1
m −1
x
ma dwa pierwiastki wtedy i tylko wtedy, gdy parametr m spełnia warunek: − 53 ≤ m < 1 .
Z warunku zadania wiemy, że te dwa pierwiastki mają spełniać nierówność
1
1
+
< 2m + 1 .
x1 x 2
Sprowadzając lewą stronę tej nierówności do wspólnego mianownika, a następnie
korzystając ze wzorów Viete’a na sumę i iloczyn pierwiastków trójmianu kwadratowego
mamy:
x + x2
1
1
+
< 2m + 1 ⇔ 1
< 2m + 1 ⇔
x1 x 2
x1 ⋅ x 2
−b
a
c
a
< 2m + 1 ⇔
−b
< 2m + 1 .
c
Po uwzględnieniu, że b = 1 − m, c = m 2 − 1 musimy rozwiązać nierówność:
−(1 − m)
m2 −1
⇔
< 2m + 1 ⇔
m −1
1
1
< 2m + 1 ⇔
< 2m + 1 ⇔
− ( 2m + 1) < 0 ⇔
(m − 1)(m + 1)
m +1
m +1
1 − (2m + 1)(m + 1)
1 − 2m 2 − 3m − 1
− 2m( m + 1,5)
<0⇔
<0⇔
< 0 ⇔ m(m + 1,5)(m + 1) > 0
m +1
m +1
m +1
Rozwiązanie nierówności m(m + 1,5)(m + 1) > 0 wymaga zbadania znaku trzech
wyrażeń: m, m + 1 i m + 1,5 . Można to zrobić budując tzw. tabelę znaków.
71
m
m + 1,5
m +1
m
m(m + 1,5)(m + 1)
−∞
...
-
-1,5
0
....
+
+
-1
0
....
+
+
-
0
0
...
+
+
+
+
Jak widzimy z powyższego zestawienia, nierówność m(m + 1,5)(m + 1) > 0
spełniona dla −1,5 < m < −1 lub m > 0 .
+∞
jest
Łącząc powyższe rozwiązanie z rozwiązaniem warunku wynikającego z faktu istnienia
dwu pierwiastków otrzymujemy ostateczne rozwiązanie naszego problemu.
− 53 − 1,5
−1
0
1
Odpowiedź. Dla −1,5 < m < −1 lub 0 < m < 1 pierwiastki równania
spełniają nierówność
1
1
+
< 2m + 1 .
x1 x 2
mx
m +1
+
= x +1
m −1
x
72
4. Literatura
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
E. Bańkowska i in. Egzamin wstępny na wyższe uczelnie. Zbiór zadań.
Wydawnictwo Podkowa, Gdańsk 1994
B. Gdowski, E. Pluciński. Zbiór zadań z matematyki dla kandydatów na wyższe
uczelnie. Wydawnictwo Naukowo-Techniczne, Warszawa 1982
J. Górczyński. Ćwiczenia z matematyki. Zeszyt 1. Funkcje i ciągi liczbowe.
WSZiM w Sochaczewie, Sochaczew 2000
J. Górczyński. Ćwiczenia z matematyki. Zeszyt 2. Granice ciągów i funkcji.
Pochodna i jej zastosowania. WSZiM w Sochaczewie, Sochaczew 2001
J. Górczyński. Ćwiczenia z matematyki. Zeszyt 3. Całki i ich zastosowania.
WSZiM w Sochaczewie, Sochaczew 2001
J. Górczyński. Ćwiczenia z matematyki. Zeszyt 4. Macierze i rozwiązywanie
równań liniowych. WSZiM w Sochaczewie, Sochaczew 2000
J. Kłopotowski i in. Matematyka dla studiów zaocznych (pod red. I. Nykowskiego). Oficyna Wydawnicza SGH, Warszawa 1995
J. Laszuk. Matematyka. Studium podstawowe. Oficyna Wydawnicza SGH,
Warszawa 1996
J. Laszuk. Matematyka. Rozwiązania zadań. Wskazówki i odpowiedzi. Studium
podstawowe. Oficyna Wydawnicza SGH, Warszawa 1997
R. Leitner, W. Żakowski. Matematyka dla kandydatów na wyższe uczelnie
techniczne. Część I. Wydawnictwo Naukowo-Techniczne, Warszawa 1984
R. Leitner, W. Żakowski. Matematyka dla kandydatów na wyższe uczelnie
techniczne. Część II. Wydawnictwo Naukowo-Techniczne, Warszawa 1984
A. Zieliński. Wykłady z matematyki praktycznej. Fundacja „Rozwój SGGW”,
Warszawa 1997
A. Zieliński. Ćwiczenia z matematyki. Zeszyt 6. Zadania powtórzeniowe z matematyki wraz z rozwiązaniami dla kandydatów na studia ekonomiczne. WSZiM
w Sochaczewie, Sochaczew 2002

1. Liczby rzeczywiste

Transkrypt

Podobne dokumenty

Dwa słowa o zadaniu M 1360

kurs przygotowawczy z matematyki dla kandydatów na studia

L3 - Wydział Matematyki - Politechnika Wrocławska

Zadanie Napisz wzór funkcji wykładniczej , gdzie 0, wiedząc, że do

Cel 10: Zmniejszyć nierówności w krajach i między krajami

Praca domowa 1 - Marek Pietrow

Regionalne Koło Matematyczne

Zadanie Naszkicuj wykres funkcji 3 dla 0 2 5 dla 0 . Na podstawie

PROGRAM INNOWACJI PEDAGOGICZNEJ Z

Rozkład na ułamki proste. Równania i nierówności wymierne.