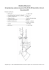Twierdzenie 5. Niech p : ˜X → X Definicja 6. Powiemy, »e p : ˜X → X

Piotr Suwara
Topologia II: 2 marca 2012
1
Twierdzenie 1
(van Kampen). U, V otwarte, ªukowo spójne podzbiory X , U ∩ V ªukowo
spójna, x0 ∈ U ∩ V . Wówczas π1 (X, x0 ) = π1 (U, x0 ) ∗π1 (U ∩V,x0 ) π1 (V, x0 ), gdzie G ∗ H sªowa
w alfabecie {g ∈ G, h ∈ H}, za± G ∗F H = G ∗ H/hi1 (f )i2 (f )−1 : f ∈ F i.
Denicja 2
(nakrycie). Powiemy, »e p : X̃ → X jest nakryciem, je±li dla ka»dego x ∈ X
istnieje Ux 3 x otwarte otoczenie takie, »e p−1 (Ux ) ∼
= Ux × T (homeomorzm), gdzie T −1
∼
przestrze« dyskretna oraz diagram p (Ux ) = Ux × T jest przemienny.
π
p
Ux
Denicja 3.
Przy oznaczeniach jak wy»ej, moc p−1 (x) jest równa T , p−1 (x) nazywamy
wªóknem p nad x. Moc T nazywamy krotno±ci¡ nakrycia w x.
Denicja 4
(podniesienie). Niech f : Y → X , p : X̃ → X nakrycie, f˜ : Y → X̃ . Powiemy,
»e f˜ jest podniesieniem f wzgl¦dem p, je±li p ◦ f˜ = f .
Twierdzenie 5.
Niech p : X̃ → X b¦dzie nakryciem, f : Y → X , Y spójna, f˜1 , f˜2 to
podniesienia f wzgl¦dem p oraz f˜1 (y0 ) = f˜2 (y0 ) dla pewnego y0 ∈ Y . Wtedy f˜1 = f˜2 .
Denicja 6. Powiemy, »e p : X̃ → X ma wªasno±¢ podnoszenia homotopii, je±li dla dowolnej
H : Y × I → X oraz h0 : Y × {0} → X̃ takich, »e p ◦ h0 = H|Y ×{0} , istnieje H̃ : Y × I → X̃
takie, »e pH̃ = H oraz H̃|Y ×{0} = h0 :
Y × {0}
h0
∃H̃
Y ×I
X̃
p
H
X
Stwierdzenie 7.
Je±li nakrycie p : X̃ → X ma wªasno±¢ podnoszenia homotopii, to podniesienie jest jednoznaczne.
Twierdzenie 8.
Wniosek 9.
Nakrycia maj¡ wªasno±¢ jednoznacznego podnoszenia homotopii.
Nakrycie ma wªasno±¢ jednoznacznego podnoszenia dróg.
Wniosek 10.
Gdy p : X̃ → X , x0 , x1 ∈ X s¡ w jednej skªadowej ªukowej spójno±ci, to
p (x0 ), p (x1 ) s¡ równoliczne (zgadza si¦ krotno±¢ nakrycia).
−1
−1