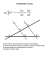Agnieszka Duszeńko

TWIERDZENIE TALESA W PRZESTRZENI
– PRACA BADAWCZA
autor
Agnieszka Duszeńko
Uniwersytet Wrocławski
Wydział Matematyki i Informatyki
2005
Na płaszczyźnie:
Najpopularniejsza, powszechnie znana wersja twierdzenia Talesa brzmi
„Jeśli ramiona kąta przetniemy dwiema (lub więcej) prostymi równoległymi, to odcinki
wyznaczone przez te proste na jednym ramieniu kąta są proporcjonalne do
odpowiednich odcinków na drugim ramieniu tego kąta”
Założenie: AC || BD
OA
Teza:
OB

OC
OD
Dowód twierdzenia wykorzystuje cechy podobieństwa trójkątów:
Trójkąty ∆OAC oraz ∆OBD są podobne, ponieważ mają równe kąty:
 i  ' oraz  i  ' są to kąty odpowiadające i równe (ponieważ proste, przy których się
znajdują są równoległe) a kąt  mają wspólny.
Stąd odpowiednie odcinki w tych trójkątach są proporcjonalne, a zatem zachodzi równość z
twierdzenia Talesa:
OA
OB

OC
OD
.
W przestrzeni:
Przeniesienie twierdzenia Talesa z płaszczyzny na przestrzeń nie jest takie oczywiste. Po
pierwsze nie wiadomo, jaki kąt przestrzenny wziąć za analogon kąta płaskiego, jak
interpretować proste równoległe i co będzie odpowiednikiem proporcjonalnych odcinków.
Podczas wielu prób zinterpretowania tego problemu powstało wiele koncepcji, wiele z nich
odrzuciłam, niektóre były trywialne (gdyż ostatecznie sprowadzały problem do płaszczyzny),
ale powstały również ciekawe pomysły. Niektóre z nich przedstawię poniżej:
I.
Pierwszy pomysł
 kąt – kąt dwuścienny
 proste – płaszczyzny równoległe do krawędzi kąta dwuściennego
 odcinki – nieograniczone pasy
W przypadku tym analogicznie jak to jest w twierdzeniu Talesa długości odcinków możemy
myśleć, że będziemy porównywać pola tych pasów. Praktycznie jednak trudno jest
powiedzieć jak to porównanie miałoby wyglądać, ponieważ pasy mają nieskończoną długość.
Jeśli by jednak przyjąć, że pole takiego pasa jest równe równy   (szer _ pasa) , to przy
porównaniu pól i tak „  -ści” się poskracają i otrzymamy „płaskie” twierdzenie Talesa.
II.
Drugi pomysł
Podobnie jak wyżej:
 kąt – kąt dwuścienny
 proste – płaszczyzny równoległe do krawędzi kąta dwuściennego
z tą różnicą, że bierzemy:
 odcinki – płaskie figury geometryczne: prostokąty, równoległoboki lub trapezy w
zależności od tego w jaki sposób obetniemy nieskończone pasy z poprzedniego
przypadku płaszczyznami nierównoległymi do krawędzi kąta.
W przypadku, gdy te płaszczyzny będą prostopadłe do krawędzi kąta otrzymamy takie
prostokąty, których jedna krawędź będzie równa odległości x pomiędzy tymi płaszczyznami.
Porównując pola tych prostokątów długość ta upraszcza się jednak i znów nasz przypadek się
„spłaszcza”.
Mamy:
ax
c x

( a  b )  x (c  d )  x
a więc
a
c
.

ab cd
Podobnie jest dla równoległoboków.
Dla trapezów natomiast próbując uogólnić dochodziłam do wielkiego wzoru, ale myślę że
również po dokładnych przekształceniach zadanie sprowadzi się do rozpatrzenia płaskiego
twierdzenia Talesa.
III. Trzeci pomysł
 kąt – kąt dwuścienny
 proste – płaszczyzny równoległe między sobą i nierównoległe do krawędzi kąta
dwuściennego
 odcinki – kąty (części półpłaszczyzn będących ścianami kąta dwuściennego zawarte
pomiędzy dwiema półprostymi o wspólnym początku i ramieniu zawartym w krawędzi
kąta dwuściennego)
Zarówno zaznaczone na czarno jak i na zielono kąty zawierają się w jednych płaszczyznach
(odpowiednio czarne w jednej i zielone w jednej) i są przystające, ponieważ są to kąty
odpowiadające. Kąty te są więc przystające. Jakakolwiek próba przeformułowania
twierdzenia Talesa na ten przypadek nie ma zatem większego sensu.
IV. Czwarty pomysł
Kolejno pomyślałam więc o kącie wielościennym.
Nasza kolejna sytuacja:
 kąt – kąt wielościenny
 proste – równoległe płaszczyzny
 odcinki – trójkąty
Jak łatwo z rysunku zauważyć odpowiednie trójkąty są podobne, a więc i ich długości boków
i ich pola są proporcjonalne (odcinki – skala k, pole – skala k2).
Jak również pola powstałych w przekroju figur są w stosunku k2, co łatwo pokazać np. w taki
sposób:
rys.1
rys.2
Dzielimy kąt wielościenny na kąty trójścienne, gdzie łatwo widać przystawanie trójkątów
powstałych w przekroju płaszczyznami równoległymi (rys.2):
 zaznaczone odpowiednie kąty na rys.2 są równe, ponieważ są to kąty odpowiadające a
płaszczyzny, które przecinały kąt są równoległe,
 analizując po kolei kąty i odcinki można sprawdzić, że wszystkie pary odpowiednich
odcinków w trójkątach powstałych w przekroju są proporcjonalne,
 stąd też i trójkąty są podobne, a zatem ich pola proporcjonalne
Ostatecznie więc odpowiednie trójkąty na rys.1 są podobne, więc i całe te przekroje są
figurami podobnymi.
V.
Piąty pomysł
Na koniec powstała jeszcze inna, całkiem różna od poprzednich koncepcja.
W tym celu przeformułowałam „płaskie” twierdzenie Talesa w taki oto sposób:
Rzut równoległy na prostą zachowuje stosunek odcinków równoległych wzajemnie do
odcinków będących ich rzutami.
I taka interpretacja przełożenia na przestrzeń:
Rzut równoległy na płaszczyznę zachowuje stosunek pól powierzchni figur (płaskich)
równoległych wzajemnie do odpowiednich figur będących ich rzutami.
Na podstawie dołączonych dalej rysunków widać, że tak jest. Można również przy programu
C.a.R zasymulować taką sytuację i obserwować że stosunek dynamicznie zmieniających się
wartości pól zadanych figur nie zmienia się. Uzasadnienie tego faktu jest więc zapewne
możliwe, ale z pewnością nie elementarne.