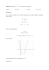Harmonogramy liniowe i diagramy Gantta

Harmonogramy liniowe i diagramy Gantta.
Na sieci czynności możemy bezpośrednio ustalić kolejność wykonywania czynności,
ale trudno bez dodatkowych obliczeń odpowiedzieć na np. pytania: ile i które czynności są
wykonywane w każdym momencie. W celu odpowiedzi na takie pytania i do rozwiązywania
wielu innych ważnych zagadnień wykorzystywane są HL - harmonogramy liniowe.
Zwykle HL budujemy na podstawie sieci czynności o numeracji właściwej. W tym
celu rysujemy poziomą oś czasową o ustalonej skali. Czynności rysujemy równolegle nad nią,
przy czym każda czynność jest przedstawiana w postaci odcinka o długości równej czasowi
trwania tej czynności. Rozpoczynamy rysowanie czynności wychodzących najpierw od
zdarzenia P0, przy czym początek wszystkich tych odcinków odpowiada umownej pionowej
linii zerowej. Odcinki te rysujemy od dołu do góry równolegle do siebie zgodnie ze wzrostem
numeru końca czynności. Dowolne inne czynności postaci (Pi,Pj) wychodzące od zdarzenia Pi
rysujemy zaczynając od umownej linii pionowej, która odpowiada najbardziej na prawo
wysuniętemu końcowi Pi spośród już narysowanych czynności. Wszystkie czynności
wychodzące od Pi rysujemy od dołu do góry równolegle do siebie zgodnie ze wzrostem
wartości Pj – końca czynności. Takie procedury powtarzamy dla wszystkich i=0,1,...,n-1, tym
samym cały HL zostaje narysowany.
Kontynuacja przykładu:
Zbudujemy HL dla SCz z naszego przykładu.
P4
P3
1
P3
P2
P1
P1
P0
P0
4
2
5
3
5
P4
3
P3
P3
P2
P5
P4
P5
6
P5
P0 3 P1
0
2
4
6
8
10
12
14
Wartości na czynnościach będą wykorzystane dalej.
Na tym HL bezpośrednio widać, ile i które czynności są bezpośrednio wykonywane w
danej chwili. Dla HL łatwo obliczyć wszystkie parametry czasowe, o których była mowa
wcześniej. W szczególności widać czas krytyczny, który jest równy rzutowi na oś czasu
najbardziej na prawo wysuniętego końca odcinka sieci czynności. Odpowiednio minimalne
momenty Tj(0) na HL równe są rzutowi najbardziej na prawo wysuniętego końca Pj na oś t. W
taki sposób otrzymujmy:
T1(0) =2,
T2(0) =4,
T3(0) =6,
T4(0) =12,
T5(0) =14- czas krytyczny.
Swobodny zapas czasu czynności (Pi,Pj). tj. wartość sij na HL jest równa odcinkowi
czasu, o który możemy przesunąć w prawo naszą czynność bez przesunięć żadnych innych
czynności. Np. dla czynności (P0,P3) s03=1.
Nieco trudniej określić jest wartości zij zupełnych zapasów czasu czynności. W tym
celu powinniśmy najpierw przesunąć w prawo na tyle ile to możliwe bez zwiększenia czasu
krytycznego wszystkie czynności występujące po danej czynności (Pi,Pj). Po takim
przygotowaniu można ustalić wartość zij jako długość odcinka, o który można przesunąć
czynność (Pi,Pj) w prawo. Przykładowo dla czynności (P0,P2), z02=3. Najpierw przesuwamy
(P2,P5) o 3 jednostki. Dla HL widać także, że czynności należące do drogi krytycznej mają
zij=0. Dowolne przesunięcie w prawo czynności krytycznej powoduje zwiększenie czasu
krytycznego.
Z HL możemy zbudować drogę krytyczną. W tym celu na HL oznaczamy wszystkie
czynności, których koniec odpowiada czasowi krytycznemu. Dalej rzutujemy początki
zaznaczonych czynności na oś czasu i oznaczamy w jakiś sposób te czynności, których końce
należą do tych rzutów.
Najciekawsze zastosowania HL polegają na: niech na SCZ oprócz czasów trwania
czynności dane są dodatkowo informacje o rodzajach i ilości środków koniecznych do
wykonywania każdej czynności (np. ilość pracowników, środki finansowe, ilość narzędzi
wszelkiego rodzaju, itp.). W celu uproszczenia, załóżmy, że analizujemy tylko jeden ze
środków koniecznych do wykonywania czynności, np. ilości pracowników. Te ilości
zapisujemy bezpośrednio na sieci czynności np. w kółkach. Następnie przenosimy te wartości
z kółek na HL zbudowany wyżej. Możemy teraz korzystając z tych informacji obliczyć ilu
wykonawców potrzebnych jest w każdej chwili. Np. moment t=1, 3+2+4=9, dla t=6 mamy
5+3+1=9, itd.
Na podstawie tych informacji możemy zbudować wykres zużycia środka, który analizujemy.
Największe trudności i najtrudniejsze zagadnienia powstają, gdy ilości potrzebnego środka są
ograniczone w każdej chwili.
Przykład: zakład wykonujący przedsięwzięcie ma tylko 9 robotników. Wtedy powstaje
pytanie, jak przekształcić HL aby wykres zużycia środka został umieszczony pod linią R=9.
Takie przekształcenie HL polega na przesunięciu w prawo niektórych czynności. To z kolei
może spowodować wzrost czasu krytycznego. Jeżeli mamy do wyboru, które czynności
przesunąć w prawo na odcinku czasowym, to ma sens przesuwać w prawo te czynności, dla
których zupełny zapas czasu jest jak największy.