n - Wkuwanko.pl

Podstawy Informatyki
Algorytmy i ich poprawność
Błędy
Błędy:
• językowe
• logiczne
Błędy językowe
• Związane ze składnią języka
• Wykrywane automatycznie przez kompilator lub interpreter
• Prosty sposób usuwania
Przykład:
//fragment programu w języku C++
.........
if(a){
................
błąd!!! Komunikat kompilatora: „Else” – brak
}
deklaracji tego identyfikatora.
Else{
Słowo kluczowe „else” powinno być napisane z
................
małej litery
}
Błędy logiczne (1)
Błędy semantyczne
Związane z semantyką języka programowania
– Kompilator w niektórych przypadkach sugeruje (ostrzega), że dana
konstrukcja może nie działać poprawnie
– Stosunkowo prosto można je zdiagnozować i usunąć
Przykład:
//fragment programu w języku C++
.........
if(i=8){
................
}
...............
Błąd semantyczny
Zamiarem programisty było sprawdzenie
czy i jest równe 8 (i==8), a nie
dokonanie podstawienia i=8 (co zawsze
jest prawdziwe)
Błędy logiczne (2)
Przykład
Błędy algorytmiczne
– Błędy logiczne wynikające z niepoprawnego rozwiązania zadania
algorytmicznego (błędny algorytm rozwiązania)
– Są niezależne od języka, w którym zaimplementowano algorytm
– Najtrudniej wykrywalne
................
Struktura „Lista”
struktura Lista{
next
info
Dane info;
Wskaźnik_Lista next; //next jest wskaźnikiem do obiektu typu Lista
};
void main(){
Wskaźnik_Lista head=Λ; //lista pusta
................
head
Λ
utworz_liste(head,plik); //utworz liste z danych w pliku „plik”
//i niech head wskazuje na pierwszy element
//tej listy
while(head){
//przegladanie elementow listy
//operacje na liscie
...................
błąd algorytmiczny
head = head->next;
}
................
}
Testowanie programów
– Testowanie odbywa się poprzez uruchamianie programu dla danych
testowych
–
Debugging – proces wielokrotnego uruchamiania programu dla
wykrycia i usunięcia błędów. Większość środowisk programistycznych
jest wyposażona w narzędzia wspomagające proces debuggowania
Obydwie metody nie dają gwarancji wykrycia i usunięcia wszystkich
błędów.
Niepoprawność algorytmu
– Wykonanie algorytmu rozwiązania zadania dla pewnego zestawu danych
zakończy się prawidłowo, ale wyniki są niepoprawne
np. źle sformułowany warunek, powinna być silna nierówność, a jest słaba
–
Działanie algorytmu dla pewnego zestawu danych zostanie przerwane;
np. dzielenie przez zero, obliczenie pierwiastka kwadratowego z liczby ujemnej
–
Algorytm dla pewnego zestawu danych działa w nieskończoność
(pętle nieskończone);
np. przy przeglądaniu listy wskaźnikowej, wskaźnik nie jest przesuwany do
następnego elementu listy
Poprawność algorytmu
Poprawność algorytmu
Zadanie algorytmiczne:
1. I – zbiór dopuszczalnych danych wejściowych
2. R – zależności między danymi wejściowymi a żądanymi wynikami
Przykład:
• Zbiór I = <N,L>, gdzie N∈ℵ+, L – lista słów.
• Zależność R – wynikiem ma być lista N-elementowa L’, utworzona ze
słów z listy L, uporządkowana leksykograficznie
• Zbiór I i relacja R są specyfikacją zadania uporządkowania listy L,
opisanego algorytmem A.
Algorytm A jest częściowo poprawny względem I i R:
∀X∈I, jeżeli A uruchomiony dla I zatrzyma się
⇒
relacja R między X a otrzymanym wynikiem jest spełniona
Algorytm A zatrzymuje się dla zbioru I, tzn. algorytm A zatrzymuje się ∀X ∈I
Algorytm A jest całkowicie poprawny względem I i R:
∀X ∈I algorytm A zatrzymuje się i daje wynik spełniający relację R
Poprawność algorytmu
Indukcja matematyczna
Niech P(n) będzie pewnym stwierdzeniem o liczbie całkowitej n. Chcemy udowodnić,
że P jest prawdziwe dla n∈ℵ+. Korzystamy z indukcji matematycznej:
1. Przedstaw dowód, że P(1) jest prawdziwe
2. Przedstaw dowód, że „jeśli wszystkie P(1), P(2), .., P(n) są prawdziwe, to P(n+1) jest
też prawdziwe”
Algorytm Euklidesa (rozszerzony)
Dane są dwie dodatnie liczby całkowite m i n. Oblicz ich największy wspólny dzielnik
(nwd) d, oraz dwie liczby całkowite a i b takie, że am + bn = d.
K1. Inicjowanie. a’ ← b ← 1; a ← b’ ← 0; c ← m; d ← n;
K2. Dzielenie. Niech q i r będą odpowiednio ilorazem i resztą z dzielenia c przez d:
c = qd + r i 0 ≤ r < d;
K3. Czy reszta zero? Jeśli r = 0, zakończ algorytm; w tym przypadku am + bn = d;
K4. Ponowienie. Przyjmij c ← d; d ← r; t ← a’; a’ ← a; a ← t – qa; t ← b’; b’ ← b;
b ← t – qb; wróć do K2.
Przykład
Niech m = 2884, n = 364
a’
a
b’
1
0
0
0
1
1
1
-1
-7
b
1
-7
8
c
2884
364
336
(-1)*2884 + 8*364 = -2884 + 2912 = 28
d
364
336
28
q
7
1
12
r
336
28
0
Poprawność algorytmu
Dowód poprawności algorytmu Euklidesa dla dowolnych m i n.
Lemat
Równości
a’m + b’n = c, am + bn = d
są prawdziwe po każdym wykonaniu kroku K2 (na podstawie faktu, że równości są
prawdziwe po pierwszym dojściu do K2 i krok K4 nie zmienia ich prawdziwości).
Stwierdzenie
Pary {m, n} i {n, r} mają ten sam zbiór wspólnych dzielników
Indukcja względem n.
1. Jeśli m jest wielokrotnością n, to algorytm działa poprawnie (pierwsze
wykonanie kroku K3). Tak jest zawsze, gdy n = 1.
2. Jeśli n > 1 i m nie jest wielokrotnością n. Algorytm po pierwszym przebiegu
przechodzi do wykonania przypisania c ← d; d ← r, oraz r <n ⇒ z założenia
indukcyjnego stwierdzamy, że końcowa wartość d jest nwd liczb n i r. Ze
stwierdzenia że, pary {m, n} i {n, r} mają te same wspólne dzielniki ⇒ wspólny
nwd. Stąd d jest nwd liczb m i n. Z lematu ⇒ am + bn = d.
Poprawność algorytmu
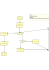
Ogólna metoda dowodzenia poprawności dowolnego algorytmu: opis schematu
blokowego algorytmu asercjami.
Asercje
Opisuje stan rzeczy w chwili, gdy wykonywane jest obliczenie strzałki w schemacie
blokowym algorytmu związanej z tą asercją.
start
A1: m > 0 , n > 0
K1. a’ ← 1;
b’ ← 0;
b ← 1;
c ← m;
a ← 0;
d ← n;
A2: c = m > 0 , d = n > 0,
a = b’ = 0, a’ = b = 1
K2. q ← iloraz(c / d);
r ← reszta(c / d);
K3. r == 0?
tak
nie
K1. c ← d; d ← r;
t ← a’; a’ ← a; a ← t – qa;
t ← b’; b’ ← b; b ← t – qb;
A3: am + bn = d, a’m + b’n = c = qd + r,
0 <= r < d, nwd(c, d) = nwd(m, n)
A4: am + bn = d = nwd(m, n)
stop
A5: am + bn = d, a’m + b’n = c = qd + r,
0 < r < d, nwd(c, d) = nwd(m, n)
A6: am + bn = d, a’m + b’n = c = qd + r,
d > 0, nwd(c, d) = nwd(m, n)
Poprawność algorytmu
Ogólna metoda polega na udowodnieniu, że dla każdego bloku zachodzi warunek:
Jeśli asercja związana z jakąkolwiek strzałką prowadzącą do bloku jest prawdziwa
zanim zostanie wykonana operacja opisywana przez blok, to wszystkie asercje
związane ze strzałkami wychodzącymi z bloku są prawdziwe po wykonaniu tej
operacji.
Z prawdziwości powyższego twierdzenia dla każdego bloku wynika, że wszystkie
asercje są prawdziwe podczas każdego wykonania algorytmu (dowód przez indukcję
względem liczby kroków obliczenia – w sensie liczby strzałek w schemacie blokowym,
po którym przeszło obliczenie).
Metoda dowodzenia poprawności algorytmów przez asercje i indukcję pochodzi od
R.W. Floyda: definicja każdej operacji języka programowania może być sformułowana
jako reguła logiczna mówiąca, że pewne asercje można udowodnić po operacji przy
założeniu, że pewne asercje były prawdziwe przed operacją.
Metoda została rozwinięta przez C.A.R. Hoare’a jako metoda niezmienników.