K NWD abaa K bb K = ⇒ = ⋅ ∧ = ⋅ , gdzie , L NWD a bb abc L bb L

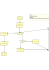
Największy Wspólny Dzielnik NWD – dowód poprawności Algorytmu Euklidesa
Największy wspólny dzielnik liczb naturalnych a, b oznaczamy przez NWD(a,b).
Własności (bardzo łatwe do udowodnienia):
Lemat
1. NWD(a,a)=a
2. NWD(a,b)=NWD(a – b,b) jeśli a > b
3. NWD(a,b)=NWD(a,b – a) jeśli a < b
Dowód (tylko wariantu 2).
Niech a > b oraz niech
K = NWD ( a, b ) ⇒ a = aK ⋅ K ∧ b = bK ⋅ K , gdzie aK , bK > 0 , aK > bK , przy czym K > 0 jest
największą liczbą o tej własności oraz niech
(*)
L = NWD ( a − b, b ) ⇒ a − b = cL ⋅ L ∧ b = bL ⋅ L , gdzie cL , bL > 0 , przy czym L > 0 jest
największą liczbą o tej własności.
(**)
Z (*) wynika, Ŝe a − b = ( aK − bK ) ⋅ K stąd K dzieli a – b (oraz oczywiście K dzieli b).
A zatem na pewno K ≤ L na mocy (**).
Z (**) wynika, Ŝe a = a − b + b = ( cL + bL ) ⋅ L stąd L dzieli a (oraz oczywiście L dzieli b).
A zatem na pewno L ≤ K na mocy (*).
Stąd K = L .
CND.
Algorytm Euklidesa
start
naturalne a, b, nwd, A, B ;
czytaj a ;
czytaj b ;
A=a;
B=b;
dopóty dopóki a ≠ b wykonuj
jeśli a > b to a = a − b ;
w przeciwnym przypadku b = b − a ;
nwd = a ;
wyświetl A ;
wyświetl B ;
wyświetl nwd ;
koniec
Rozpatrzmy funkcję zdaniową P ( a, b ) zdefiniowaną następująco:
P ( a, b ) =  a > 0 ∧ b > 0 ∧ NWD ( a, b ) = NWD ( A, B ) 
gdzie a, b, A, B są identyfikatorami zmiennych zdefiniowanych w Algorytmie Euklidesa
Dowód poprawności algorytmu sprowadza się do stwierdzenia, Ŝe funkcja zadaniowa
P ( a, b ) jest prawdziwa w kaŜdym kroku algorytmu oraz, Ŝe liczba kroków algorytmu
jest liczbą skończoną.
Dowód (por. np. Turski W.M., Propedeutyka Informatyki, PWN).
Bezpośrednio przed rozpoczęciem iteracji funkcja P ( a, b ) jest oczywiście prawdziwa pod
warunkiem, Ŝe wczytamy liczby naturalne a i b.
Iteracja jest wykonywana pod warunkiem, Ŝe a ≠ b , czyli mamy albo przypadek a > b albo
przypadek a < b .
Jeśli a > b , to działanie wykonywane w obrębie iterowanej instrukcji nie zmieni b, natomiast
a pozostanie dodatnie. Ponadto będzie prawdziwa relacja NWD ( a, b ) = NWD ( A, B ) na mocy
Lematu (wariant 2). A zatem wartość logiczna funkcji P ( a, b ) będzie prawdą.
Podobne rozumowanie przeprowadzamy dla przypadku a < b .
Iteracja moŜe zakończyć się tylko w przypadku kiedy a = b , przy czym zawsze będzie
spełniony warunek a > 0 ∧ b > 0 . A zatem funkcja P ( a, b ) takŜe i w tym szczególnym
przypadku będzie miała wartość logiczną prawda (mówimy wtedy, Ŝe funkcja P ( a, b ) jest
niezmiennikiem iteracji). Instrukcje, które następują po instrukcji pętli nie mają juŜ wpływu
na wartość logiczną funkcji P ( a, b ) .
ZauwaŜmy ponadto, Ŝe jeśli a = b , to na mocy Lematu (wariant 1)
NWD (a, b) = NWD (a, a ) = a i skoro funkcja P ( a, b ) jest prawdziwa w kaŜdym kroku
algorytmu (jak to zostało wykazane wyŜej), więc NWD ( A, B ) = a = nwd (po podstawieniu a
do nwd ).
Pozostaje jeszcze do udowodnienia, Ŝe iteracja musi się zakończyć, ale zauwaŜmy, Ŝe wobec
zmniejszania liczby dodatniej o liczbę dodatnią w taki sposób, Ŝe wynik zawsze pozostaje
dodatni, nie jest zatem moŜliwe (wobec załoŜonej skończoności wczytywanych liczb a i b)
aby instrukcje te mogły być powtarzane nieskończoną liczbę razy.
CND.