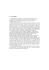Ruch złożony punktu

5.4.1. Ruch unoszenia, względny i bezwzględny
Przy omawianiu ruchu punktu lub bryły zakładaliśmy, że punkt lub bryła
poruszały się względem układu odniesienia x, y, z uważanego za nieruchomy.
Można rozpatrzyć taki
z′
przypadek, że wspomniany
z
układ odniesienia będzie się
y′
poruszał względem innego
układu, uważanego wtedy za
nieruchomy. Wówczas ruch
O′
r′
punktu lub bryły nazywamy
ruchem złożonym.
M
rO′
Ruch punktu lub bryły
L
r
względem układu
Lw
O
nieruchomego nazywamy
y
ruchem bezwzględnym, a ruch
tego samego punktu lub bryły
x′
x
względem układu ruchomego
ruchem względnym.
Rys. 5.24. Ruch złożony punktu
Ruch ruchomego układu odniesienia względem nieruchomego nazywamy ruchem
unoszenia.
W dalszej części rozpatrzymy jedynie ruch złożony punktu. Niech punkt M
porusza się w sposób dowolny, nie związany ani z nieruchomym układem
odniesienia x, y, z, ani z ruchomym x ′, y ′, z ′ (rys. 5.24). Jeżeli ruch tego punktu
będzie obserwowany przez dwóch obserwatorów − jednego związanego z układem
nieruchomym x, y, z, a drugiego związanego z układem ruchomym x ′ , y ′ , z ′ − to
każdy z obserwatorów będzie „widział” ruch punktu M w inny sposób (inny tor,
prędkość, przyśpieszenie).
Tor, jaki zakreśli punkt M w układzie nieruchomym, nazywamy torem
bezwzględnym L, a w układzie ruchomym torem względnym Lw. Każdy z punktów
toru względnego, zatem i punkt znajdujący się w tym samym miejscu co punkt M,
zakreśli pewien tor Lu. Ruch tego punktu względem układu nieruchomego
nazywamy ruchem unoszenia punktu M w rozważanej chwili.
5.4.2. Prędkość i przyśpieszenie w ruchu złożonym punktu
W celu wyprowadzenia wzorów na prędkość i przyśpieszenie punktu M
postąpimy podobnie jak podczas rozpatrywania kinematyki dowolnego punktu
bryły w ruchu ogólnym, ale teraz punkt ten będzie się poruszał względem bryły.
Zatem wektor wodzący r ′ punktu M w układzie ruchomym x ′ , y ′ , z ′ nie będzie
stały, będzie się zmieniał zarówno jego kierunek, jak i moduł:
r ′ = r ′ ≠ const .
(a)
Wektor wodzący punktu M, zgodnie z rys. 5.24, jest sumą dwóch wektorów:
r = rO′ + r ′ .
(5.76)
Podobnie jak w ruchu ogólnym bryły (p. 5.3.2) wektor rO′ jest wektorem
łączącym początki obu układów współrzędnych. Zapiszemy go analitycznie w
nieruchomym układzie współrzędnych x, y, z:
rO′ = x O′ i + y O′ j+ z O′ k .
(5.77)
Wektor r ′ jest wektorem wodzącym punktu M w układzie x ′ , y ′ , z ′ . Można
go wyrazić za pomocą współrzędnych w tym układzie:
r ′ = x ′ i ′+ y ′ j′+ z′ k ′ .
(5.78)
Współrzędne tego wektora na podstawie wzoru (a) będą się zmieniać wraz z
ruchem punktu M względem układu ruchomego x ′ , y ′ , z ′ . Można je zatem zapisać
w postaci funkcji czasu, które będą równaniami ruchu względnego punktu M:
x ′ = x ′ ( t ), y ′ = y ′ ( t ), z ′ = z ′ ( t ) .
(5.79)
Prędkość punktu M jest pochodną wektora wodzącego (5.76) względem czasu:
v=
d rO′ d r ′
+
.
dt
dt
(5.80)
Pochodna wektora rO′ jest znaną z p. 5.3.2 prędkością początku O ′ ruchomego
układu współrzędnych:
dr
dx
dy
dz
(b)
v O ′ = O ′ = O ′ i + O ′ j+ O ′ k .
dt
dt
dt
dt
Pochodna wektora r ′ po zróżniczkowaniu wzoru (5.78) ma postać:
d r ′ dx ′
dy ′
dz ′
d i′
d j′
d k′
=
i ′+
j′+
k ′+ x ′
+ y′
+ z′
.
dt
dt
dt
dt
dt
dt
dt
(c)
Pierwsze trzy wyrazy w powyższym wzorze przedstawiają prędkość względną v w
punktu M:
dx ′
dy ′
dz ′
vw =
i ′+
j′+
k′ .
(5.81)
dt
dt
dt
Po podstawieniu do trzech pozostałych wyrazów wzorów (5.31) na pochodne
wersorów i ′ , j′, k ′ otrzymamy:
d r′
= v w + x ′(ω× i ′) + y ′(ω× j′) + z ′(ω× k ′) =
dt
= v w + ω× (x ′ i ′+ y′ j′+ z ′ k ′).
Wyrażenie występujące w nawiasie, zgodnie ze wzorem (5.80), jest wektorem
wodzącym punktu M. Zatem powyższy wzór upraszcza się do postaci:
d r′
= v w + ω× r ′ .
dt
(d)
Po podstawieniu do wzoru (5.80) oznaczenia (b) oraz wzoru (d) otrzymamy
zależność na prędkość punktu M w ruchu złożonym względem nieruchomego
układu odniesienia (prędkość bezwzględną):
v = v O′ + ω× r ′+ v w .
(5.82)
Po porównaniu ze wzorem (5.32) widzimy, że pierwsze dwa wyrazy w tym wzorze
przedstawiają prędkość punktu bryły znajdującego się w tym samym miejscu co
punkt M, zatem jest to prędkość unoszenia:
v u = v O′ + ω× r ′ .
(5.83)
Po uwzględnieniu tego oznaczenia we wzorze (5.82) zauważymy, że prędkość
bezwzględna v w ruchu złożonym punktu jest sumą prędkości unoszenia v u i
prędkości względnej v w :
v = vu + vw .
(5.84)
Przyśpieszenie bezwzględne a otrzymamy, obliczając pochodną względem czasu
prędkości bezwzględnej w postaci (5.82):
a=
d v d v O′ d ω
d r′ d v w
+
=
+
× r ′+ ω×
.
dt
dt
dt
dt
dt
(e)
d v O′
dt
(f)
Pochodna
a O′ =
jest przyśpieszeniem punktu O ′ , a pochodna
dω
=ε
dt
(g)
przyśpieszeniem kątowym bryły.
Występującą we wzorze (e) pochodną wektora r ′ względem czasu
obliczyliśmy już przy wyprowadzaniu wzoru na prędkość punktu M. Jest ona dana
wzorem (d). W celu obliczenia pochodnej prędkości względnej v w względem
czasu zróżniczkujemy wzór (5.81) oraz wykorzystamy zależności (5.31):
d v w d 2 x′
d 2 y′
d 2 z′
dx ′ d i ′ dy ′ d j′ dz ′ d k ′
′
′
+
+
=
= 2 i + 2 j + 2 k ′+
dt
dt dt
dt dt
dt dt
dt
dt
dt
′
′
dx ′
(ω× i ′) + dy (ω× j′) + dz (ω× k ′) =
= aw +
dt
dt
dt
dy ′
dz ′ ⎞
⎛ dx ′
= a w + ω× ⎜
i ′+
j′+
k ′ ⎟ = a w + ω× v w ,
dt
dt ⎠
⎝ dt
gdzie aw jest przyśpieszeniem względnym punktu M:
d 2 x′
d 2 y′
d 2 z′
a w = 2 i ′+ 2 j′+ 2 k ′ .
dt
dt
dt
(h)
(5.85)
Po uwzględnieniu we wzorze (e) oznaczeń (f) i (g) oraz wzoru (h) otrzymamy
przyśpieszenie a punktu M.
a = a O′ + ε× r ′+ ω× (ω× r ′+ v w ) + a w + ω× v w =
= a O′ + ε× r ′+ ω× (ω× r ′) + a w + 2 ω× v w .
(5.86)
Pierwsze trzy wyrazy w tym wzorze znamy z ruchu ogólnego bryły jako
przyśpieszenie dowolnego punktu bryły (wzór 5.33), a więc jest to przyśpieszenie
unoszenia a u :
a u = a O′ + ε× r ′+ ω× (ω× r ′) .
(5.87)
Z kolei podwojony iloczyn wektorowy prędkości kątowej i prędkości względnej
v w jest przyśpieszeniem znanym jako przyśpieszenie Coriolisa:
a C = 2 ω× v w .
(5.88)
Tak więc przyśpieszenie bezwzględne a punktu M w ruchu złożonym jest
równe sumie trzech przyśpieszeń: unoszenia a u , względnego a w i Coriolisa a C :
a = au + aw + aC .
(5.89)
Przyśpieszenie Coriolisa jest dodatkowym przyśpieszeniem wynikającym z
ruchu obrotowego układu unoszenia. Można udowodnić [9], że jest ono wywołane
zmianą wektora prędkości względnej v w wskutek jego obrotu z prędkością kątową
oraz zmianą wektora prędkości unoszenia v u spowodowaną przemieszczaniem
się punktu M z prędkością względną v w .
Z własności iloczynu wektorowego wynika, że przyśpieszenie Coriolisa będzie
równe zeru w trzech przypadkach:
a) gdy ω = 0, wtedy ruch unoszenia jest ruchem postępowym,
b) gdy wektory prędkości kątowej ω i prędkości względnej v w punktu M są
równoległe,
c) gdy prędkość względna v w punktu M w pewnej chwili jest równa zeru.
W zagadnieniach technicznych najczęściej przyjmujemy, że układ odniesienia
związany z Ziemią jest nieruchomy. Tym samym pomijamy przyśpieszenie
Coriolisa działające na obiekty poruszające się względem Ziemi, np. pojazdy, a
wywołane jej obrotem wokół własnej osi. Takie postępowanie jest
usprawiedliwione, ponieważ przyśpieszenie to jest bardzo małe [11]. Jednak
przyśpieszenie Coriolisa towarzyszy wielu zjawiskom występującym w przyrodzie,
wywołanym obrotem kuli ziemskiej. Do zjawisk tych należą przykładowo kierunki
prądów morskich i wiatrów.
Przykład 5.7. Pozioma rurka obraca się wokół pionowej osi z, przechodzącej
przez jej środek (rys. 5.25a), zgodnie z równaniem ruchu: ϕ = 10 t − 1t 2 , gdzie
czas t jest wyrażony w sekundach, a kąt ϕ w radianach. Wewnątrz rurki porusza się
punkt M zgodnie równaniem: OM = s = 15sin πt / 3 [cm] . Obliczyć prędkość i
przyśpieszenie bezwzględne punktu M dla czasu t 1 = 1 s .
a)
b)
y
z
vu
ω
vM
O
s
O
M
s
vw x
M
y
c)
ϕ
y
ac
ε
O
a nu
aw
s
ω
M
x
a su
Rys. 5.25. Wyznaczenie prędkości i przyśpieszenia punktu M w ruchu złożonym
Rozwiązanie. Punkt M porusza się ruchem złożonym z ruchu unoszenia
wywołanego obrotem rurki i ruchu względnego względem rurki. Prędkość
bezwzględną punktu M obliczymy ze wzoru (5.84):
vM = vu + vw .
(a)
Wartość prędkości unoszenia punktu M wynikająca z ruchu obrotowego rurki
v u = ωs = (10 − 2t )15sin
π
π
t = (150 − 30t )sin t ,
3
3
gdzie ω jest wartością prędkości kątowej rurki:
ω=
[ ]
dϕ
= 10 − 2t s −1 .
dt
Wartość prędkości względnej punktu M
vw =
ds
π
π
π
= 15 ⋅ cos t = 5πcos t .
dt
3
3
3
Wektory prędkości unoszenia i prędkości względnej zaznaczono na rys. 5.25b
przedstawiającym rurkę w rzucie z góry. Dla czasu t 1 = 1 s otrzymujemy:
v u = (150 − 30)sin
v w = 5πcos
π
= 60 3 = 103,9 cm / s,
3
π
= 2,5π = 7,85 cm / s.
3
Ponieważ wektory tych prędkości są prostopadłe, wartość prędkości bezwzględnej
punktu M
v M = v 2u + v 2w = 103,9 2 + 7,85 2 = 104,20 cm / s .
Przyśpieszenie bezwzględne punktu M obliczymy ze wzoru (5.89):
a = a u + a w + a C = a su + a nu + a w + a c .
(b)
Wartości przyśpieszeń w ruchu unoszenia są następujące:
π
π ⎫
t = −30sin t ,⎪
3
3
⎪⎪
π
2
n
2
a u = ω s = 15(10 − 2 t ) sin t ,
⎬
3
⎪
dω
⎪
ε=
= −2s − 2 .
⎪⎭
dt
a su = εs = −2 ⋅ 15cos
(c)
Wartość przyśpieszenia względnego punktu M obliczymy ze wzoru:
aw =
dv w
5
π
= − π 2 sin t .
dt
3
3
(d)
Z kolei przyśpieszenie Coriolisa wyraża wzór (5.88):
a C = 2 ω× v w ,
a jego wartość
a c = 2ωv w sin
π
π
π
= 10(10 − 2 t )πcos t = (100 − 20t )πcos t .
2
3
3
(e)
Wektory składowych przyśpieszeń występujące we wzorze (b) przedstawiono na
rys. 2.25c. Wartości tych przyśpieszeń w chwili t 1 otrzymamy po podstawieniu do
wzorów (c), (d) i (e) t = t 1 = 1 s :
π
= −15 3 = −25,98 cm / s 2 ,
3
π
a nu = 8 2 ⋅ 15sin = 480 3 = 831,38 cm / s 2 ,
3
a su = 30sin
5
5 3 2
π
a w = − π 2 sin = −
π = −14,25 cm / s 2 ,
3
3
6
π
a c = 80πcos = 40π = 125,66 cm / s 2 .
3
Na podstawie rys. 5.25c wartość przyśpieszenia bezwzględnego punktu M
obliczymy ze wzoru:
aM =
(a
w
+ a un
) + (a
2
c
− a su
)
2
= 845,632 + 99,68 2 = 851,48 cm / s 2 .