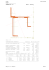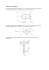Wyznaczyć główne, centralne momenty bezwładności powierzchni

Wyznaczyć główne, centralne momenty bezwładności powierzchni przedstawionej na rysunku.
Oznaczenia:
x, y
xc, yc
–
–
xcg, ycg
A1, A2, A3
C1, C2, C3
C
xc1, xc2, xc3, yc1, yc2, yc3
xc, yc
Sx, Sy
Ix1 … Ix3, Iy1 … Iy3
Ixc1 … Ixc3, Iyc1 … Iyc3
Ix, Iy
Ixc, Iyc
Ixc1yc1 … … Ixc3yc3
Ix1y1 … Ix3y3
Ixy
Ixcyc
Ixcg, Iycg
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
osie początkowego układu współrzędnych,
osie centralnego układu współrzędnych (czyli przechodzące przez
środek ciężkości figury), równoległe do osi układu x, y,
główne, centralne osie bezwładności,
pola powierzchni figur składowych,
środki ciężkości figur składowych,
środek ciężkości całej figury,
współrzędne środków ciężkości pól A1, A2, A3, w układzie x, y,
współrzędne środka ciężkości całej figury w układzie x, y,
momenty statyczne figury w układzie x, y,
osiowe momenty bezwładności pól A1, A2, A3 w układzie x, y,
osiowe, centralne momenty bezwładności pól A1, A2, A3,
osiowe momenty bezwładności całej figury w układzie x, y,
osiowe momenty bezwładności całej figury w układzie xc, yc,
momenty odśrodkowe pól A1, A2, A3 względem ich osi centralnych,
momenty odśrodkowe pól A1, A2, A3 w układzie x, y,
moment odśrodkowy figury w układzie x, y,
moment odśrodkowy figury w układzie xc, yc,
główne, centralne momenty bezwładności figury.
Obliczamy pola powierzchni figur składowych i współrzędne ich środków ciężkości:
A1 =
π ⋅ 2,52
2
A2 = 1,5 cm 2 ,
= 9,817 cm 2 ,
xc1 = 0,
xc 2 = −0,75cm,
yc1 = 1,061cm,
yc 2 = 0,5cm,
A3 = π ⋅ 0,52 = 0,785 cm 2 , xc 3 = 0,
yc 3 = 1,75 cm,
A = A1 − A2 − A3 = 7,532 cm .
2
Momenty statyczne całej powierzchni:
Względem osi x: Sx = A1⋅yc1 - A2⋅yc2 - A3⋅yc3 = 9,817·1,061 – 1,5·0,5 – 0,785 = 8,292 cm3,
względem osi y: Sy = A1⋅xc1 - A2⋅xc2 - A3⋅xc3 = 9,817·0 – 1,5·(-0,75) – 0,875·1,125 = 1,125 cm3,
Współrzędne środka ciężkości powierzchni:
xc =
Sy
=
A
1,125
= 0,149 cm,
7,532
yc =
S x 8,292
=
= 1,1cm,
A 7,532
Momenty bezwładności względem osi układu x, y:
Oś x przechodzi przez krawędzie pól 1 i 2, Moment bezwładności pola 3 obliczamy stosując twierdzenie
Steinera:
Ix =
π ⋅ 2,5 4 1,5 ⋅13
8
−
3
 π ⋅ 0,5 4

−
+ 1,75 2 ⋅ 0,785 = 15,34 − 0,5 − 2,453 = 12,387 cm 4 ,
 4

Oś y przechodzi przez krawędź figury 2 i środki ciężkości figur 1 i 3, zatem:
I
yc 3
67
8
6
78 1⋅1,53 π ⋅ 0,5 4
I y = 15,34 −
−
= 15,34 − 1,125 − 0,049 = 14,166 cm 4
3
4
I y 1 = I x1
Moment odśrodkowy:
I
I x1 y 1
x2 y2
4448 I x}3 y 3
} 64447
I xy = 0 − [0 + (−0,75) ⋅ 0,5 ⋅1,5] − 0 = 0,5625 cm 4
Momenty bezwładności względem osi centralnych xc, yc:
Ixc = Ix – yc2⋅A = 12,387-1,1012·7,532 = 3,2567 cm4,
Iyc = Iy – xc2⋅A = 14,166 – 0,1492·7,532 = 13,9988 cm4,
Ixcyc = Ixy - xc⋅yc⋅A = 0,5625 – 1,101·0,149·7,532 = -0,6731 cm4.
Kąt między układem osi głównych a układem xc, yc :
tg (2φ ) =
2 ⋅ (− 0,6731)
= −0,1253, 2φ = −7,143o , φ = −3,571o.
13,9988 − 3,2567
Główne, centralne momenty bezwładności powierzchni:
I xcg = I xc ⋅ cos 2 φ + I yc ⋅ sin 2 φ − I xcyc ⋅ sin 2φ = 3,2567 ⋅ 0,998 + 13,9988 ⋅ 0,0038 − (− 0,6731) ⋅ (−0,124) = 3,22 cm4 = I min
I ycg = I xc ⋅ sin 2 φ + I yc ⋅ cos2 φ + I xcyc ⋅ sin 2φ = 3,2567 ⋅ 0,0038 + 13,9988 ⋅ 0,998 + (− 0,6731) ⋅ (−0,124) = 14,065 = I max
Moment bezwładności Ixcg < Ixc jest najmniejszy z możliwych dla danej powierzchni, moment Iycg >Iyc jest
największy.