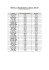Programowanie dynamiczne

D. Miszczyńska, M. Miszczyński, KBO UŁ, Elementy programowania dynamicznego
1
Elementy PROGRAMOWANIA DYNAMICZNEGO (PD)
Rozważamy n-etapowy proces decyzyjny:
t
stan początkowy
decyzja
etap 1
etap 2
...
etap n-1
x1
yn
y n 1
y2
y1
etap n
x n 1
x2
xn
Stan procesu na początek każdego etapu t określa zmienna stanu (zmienna fazowa)
y t ze zbioru Yt zwanego przestrzenią stanu (przestrzenią fazową); y t  Yt .
Decyzję w każdym etapie określa zmienna decyzyjna x t ze zbioru X t  yt  zwanego
zbiorem decyzji dopuszczalnych;
xt  X t  y t  .
Dla każdego etapu t znamy funkcję transformacji stanu (funkcja przejścia):
yt 1   t  yt , xt 
Oznacza to, że stan procesu na początek następnego (t+1) etapu zależy wyłącznie
od stanu procesu na początku etapu aktualnego (t) oraz od decyzji podjętej w
aktualnym (t) etapie.
Wielkość korzyści (strat) dla etapu t jest opisana za pomocą funkcji korzyści
bieżącej:
Ft  yt , xt 
Wielkość korzyści (strat) n-etapowego procesu jest opisana za pomocą funkcji
korzyści procesu:
F   y1, x1, y2 , x2 ,, yn 1, xn 1, yn , xn  
n
 F y , x 
t
t
t
t 1
Funkcja korzyści procesu n-etapowego jest więc funkcją:
 addytywną oraz
 rozłączną między etapami procesu ze względu na zmienne
Ogólne zagadnienie PD można sformułować następująco:
yt
n
oraz
F   y1 , x1 , y 2 , x2 ,, y n1 , xn1 , y n , xn    Ft  yt , xt   max(min)
t 1
przy ograniczeniach
yt 1   t  yt , xt 
y t  Yt
xt  X t  y t 
t  1,2,  , n  1, n
xt .
D. Miszczyńska, M. Miszczyński, KBO UŁ, Elementy programowania dynamicznego
2
Procedura PD
U podstaw procedury PD leży zasada optymalności Bellmana:
„Polityka optymalna ma tę własność, że niezależnie od stanu
początkowego procesu oraz decyzji określających dojście do danego stanu
w wybranym etapie, pozostałe decyzje muszą stanowić politykę
optymalną z danego etapu do etapu końcowego procesu”.
Inaczej mówiąc: nie jest ważne jak dotarłeś do danego etapu, dalej musisz
postępować optymalnie.
Procedura PD jest zawsze postępowaniem 2-fazowym.
1. Faza I („wstecz”) – znajdowanie warunkowego sterowania
optymalnego x  y  w każdym etapie t w kolejności: od etapu n
(ostatniego) do etapu 1 (pierwszego); t  n, n  1,,2,1 .
*
t
t
2. Faza II („do przodu”) – znajdowanie bezwarunkowego
sterowania optymalnego x w każdym etapie t w kolejności:
od etapu 1 (pierwszego) do etapu n (ostatniego); t  1,2,, n  1, n .
*
t
Dla uproszczenia zapisu przyjmujemy, że poszukujemy wartości największej
funkcji korzyści procesu, tj.
n
F   y1 , x1 , y 2 , x2 ,, y n1 , xn1 , y n , xn    Ft  yt , xt   max
t 1
D. Miszczyńska, M. Miszczyński, KBO UŁ, Elementy programowania dynamicznego
3
Faza I („wstecz”)
Etap n (ostatni) poszukujemy warunkowej decyzji optymalnej xn*  yn 
wykorzystując wyłącznie funkcję korzyści bieżącej Fn  y n , xn  etapu n.
xn*  y n  :
Gn  y n   max Fn  y n , x n 
xn  X n  y n 
Etap t ( t  n  1, n  2,,2,1 ) poszukujemy warunkowej decyzji optymalnej
x  y  wykorzystując funkcję korzyści bieżącej F  y , x  etapu t oraz
optymalną łączną korzyść warunkową dla wszystkich pozostałych etapów
od następnego(t+1) do ostatniego (n), tj. wielkość G  y  , którą można
zapisać na mocy równania transformacji stanu y    y , x  jako G   y , x  . W ten
sposób dla etapu t przeszukiwana funkcja będzie zawsze funkcją zmiennej
stanu i zmiennej decyzyjnej wyłącznie aktualnego etapu t.
*
t
t
t
t
t
t 1
t 1
xt*  yt  :
t
t
t
t 1
t 1
t
t
t
Gt  y t   max Ft  y t , xt   Gt 1  t  y t , xt 
xt X t  yt 
Wynikiem fazy I jest ciąg warunkowych sterowań optymalnych
x  y , x  y ,, x  y , x  y oraz warunkowa optymalna wartość funkcji
korzyści procesu G  y .
*
n
n
*
n 1
*
2
n 1
*
1
2
1
1
1
Faza II („do przodu”)
Zakładamy, że stan początkowy procesu y (początek etapu 1) jest znany
lub może być wskazany. Znajomość stanu y pozwala na wyznaczenie
sterowania bezwarunkowego x poprzez wykorzystanie znajomości
funkcji sterowania warunkowego x  y  . To z kolei pozwala na wyznaczenie
stanu początkowego y poprzez wykorzystanie równania transformacji
stanu y   y , x  . Powielając rekurencyjnie opisane postępowanie
docieramy do ostatniego etapu (n).
1
1
*
1
*
1
2
2
1
1
*
1
1
D. Miszczyńska, M. Miszczyński, KBO UŁ, Elementy programowania dynamicznego
Etap
Stan
początkowy
Sterowanie
bezwarunkowe
4
Stan procesu w
następnym etapie
yt
xt*  xt*  yt 
y1
x1*  x1*  y1 
y2
y2
x 2*  x 2*  y 2 
y3
.
.
.
.
.
.
1
2
.
.
.
n-1
y n 1
xn*1  xn*1  yn1 
n
yn
xn*  xn*  yn 
 
  y , x 
  y , x 
yt 1  t yt , xt*
1
1
*
1
2
2
*
2
.
.

y
yn1   n2 yn2 , xn*2
yn   n1
n 1
, xn*1


Na ogół nas nie
interesuje
Optymalną wartość funkcji korzyści procesu F wyznaczamy dzięki
znajomości stanu procesu na początek etapu 1 ( y ) wykorzystując
zależność F  G  y .
max
1
max
1
1
D. Miszczyńska, M. Miszczyński, KBO UŁ, Elementy programowania dynamicznego
Przykład 1
5
(Zagadnienie dyliżansu1)
„W dawnych czasach żył Mr Mark Off, który postanowił poszukać szczęścia w San
Francisco. Jedynym środkiem transportu ze Wschodu, gdzie mieszkał, na Zachód był dyliżans.
Agent z biura podróży przedstawił mu mapę Stanów Zjednoczonych (patrz rys.), na której
były zaznaczone różne możliwe trasy dyliżansów. Każdy kwadrat na mapie reprezentuje
stan. Stany dla wygody ponumerowano. Zauważmy, że cała podróż ze Wschodu na Zachód
składa się z czterech etapów niezależnie od wyboru drogi.
Ponieważ podróżny wiedział, że podróż stanowi poważne niebezpieczeństwo dla jego
zdrowia i życia, postanowił przed wyruszeniem z domu ubezpieczyć się. Cena polisy
ubezpieczeniowej zależała od wyboru drogi; im większe niebezpieczeństwa czyhały na
podróżnych, tym droższa była polisa bez-pieczeniowa. Niech cij oznacza cenę polisy
ubezpieczeniowej na trasie od stanu i do stanu j. Przykładowe wartości cij zaznaczono na
rysunku.
Celem Marka Off był wybór takiej trasy ze Wschodu na Zachód, która minimalizowała
ogólny koszt ubezpieczenia.
etap 4
etap 3
etap2
etap1
„
1
przykład pochodzi z pracy Wagner H.M., Badania operacyjne. Zastosowania w zarządzaniu, PWE, Warszawa,1980, s. 296
D. Miszczyńska, M. Miszczyński, KBO UŁ, Elementy programowania dynamicznego
Przykład 1
6
(Zagadnienie dyliżansu - ROZWIĄZANIE)
Etap 1
Stan początkowy
Decyzja
Etap 2
Etap 3
Etap 4
y1=1
y2{2,3,4}
y3{5,6,7}
x1(y1){2,3,4}
x2(y2=2){5,6}
x3(y3=5){8,9}
x2(y2=3){5,6,7} x3(y3=6){8,9}
x2(y2=4){6,7}
x3(y3=7){8,9}
„ t”
y4{8,9}
x4(y4=8)=10
x4(y4=9)=10
FAZA I („wstecz”)
Etap 4
Etap 3
F4(y4,x4)
G3(y3, x3)=F3(y3, x3) + G4(y4)
G4(y4) x4*(y4)
y4 \ x4
10
8
1
1
9
4
4
x3*(y3)
y3 \ x3
8
9
10
5
7+1=8
5+4=9
8
8
10
6
3+1=4
4+4=8
4
8
7
7+1=8
1+4=5
5
9
Etap 2
Etap 1
G2(y2, x2)=F2(y2, x2) +
+ G3(y3)
G2(y2, x2)=F2(y2, x2) + G3(y3)
G2(y2) x2*(y2)
y2 \ x2
G3(y3)
5
6
2
10+8=18 12+4=16
3
5+8=13
4
×
7
y1 \ x1
×
16
6
7+5=12
12
7
15+4=19 13+5=18
18
7
10+4=14
1
2
18
Etap
Stan
początkowy
Decyzja
Stan
następny
1
y1 = 1
x1* = x1*(y1= 1) = 3
y2 = 3
2
y2 = 3
x2* = x2*(y2= 3) = 7
y3 = 7
3
y3 = 7
x3* = x3*(y3= 7) = 9
y4 = 9
4
y4 = 9
x4* = x4*(y4= 9) = 10
„y5” = 10
17
x1*(y1)
17
3
4
2+16= 5+12= 1+18=
FAZA II („do przodu”)
Fmin = G1(y1=1) = 17
3
G1(y1)
19
D. Miszczyńska, M. Miszczyński, KBO UŁ, Elementy programowania dynamicznego
Przykład 2
7
(zarządzanie zapasami – popyt dany)
Ustal dla pewnego dobra program produkcyjny {xt} dla 4 kolejnych okresów (t)
minimalizujący łączne koszty produkcji i koszty magazynowania w okresach 14.
Popyt (Dt) na produkowane dobro jest stały w każdym okresie t: Dt  3 dla t=1,2,3,4.
max
Możliwości produkcyjne (xt) w każdym etapie t : xt  5 .
Koszty produkcji (C(xt)) ilości xt>0 w okresie t : C xt   15  5 xt .
Koszty magazynowania są naliczane od stanu magazynu na koniec okresu. Oznacza to,
że są one naliczane od stanu początkowego magazynu w okresie następnym (Zt+1).
Koszt przetrzymywanie jednostki dobra w okresie t : hZ t   3  Z t .
„Korzyść” bieżąca etapu t wynosi zatem: F Z t , xt   C xt   hZ t  .
Pojemność magazynu wynosi 4 jednostki (Zmax=4).
Cała produkcja okresu 1-4 musi być sprzedana. Oznacza to, że Z5 (maj)=0.
Równanie transformacji stanu ma postać: yt 1   yt , x t   yt  xt  Dt  yt  xt  3 .
Schemat postępowania
Etap 1
styczeń
Etap 2
luty
Etap 3
marzec
Etap 4
kwiecień
Stan początkowy
y1=Z1=0
y2=Z24
y3=Z34
y4=Z44
Decyzja
x15
x25
x35
x43
t
maj
y5=Z5=0

FAZA I („wstecz”)
Etap 4 (kwiecień)
G4(y4, x4)=F4(y4, x4) = h4(y4) + C(x4)
G4(y4)
x4*(y4)
y4 \ x4
0
1
2
3
4
5
0
×
×
×
0+30
×
×
30
3
1
×
×
3+25
×
×
×
28
2
2
×
6+20
×
×
×
×
26
1
3
9+0
×
×
×
×
×
9
0
4
×
×
×
×
×
×
×
×
D. Miszczyńska, M. Miszczyński, KBO UŁ, Elementy programowania dynamicznego
8
Etap 3 (marzec+kwiecień)
G3(y3, x3)=F3(y3, x3) + G4(y4) = h3(y3) + C(x3) + G4(y4)
G3(y3)
x3*(y3)
y3 \ x3
0
1
2
3
4
5
0



0+30+30
0+35+28
0+40+26
60
3
1


3+25+30
3+30+28
3+35+26
3+40+9
52
5
2

6+20+30
6+25+28
6+30+26
6+35+9

50
4
3
9+0+30
9+20+28
9+25+26
9+30+9


39
0
4
12+0+28
12+20+26
12+25+9



40
0
G2(y2)
x2*(y2)
Etap 2 (luty+marzec+kwiecień)
G2(y2, x2)=F2(y2, x2) + G3(y3) = h2(y2) + C(x2) + G3(y3)
y2 \ x2
0
1
2
3
4
5
0



0+30+60
0+35+52
0+40+50
87
4
1


3+25+60
3+30+52
3+35+50
3+40+39
82
5
2

6+20+60
6+25+52
6+30+50
6+35+39

80
4
3
9+0+60
9+20+52
9+25+50
9+30+39


69
0
4
12+0+52
12+20+50 12+25+39



64
0
G1(y1)
x1*(y1)
117
3 ; 4
Etap 1 (styczeń+luty+marzec+kwiecień)
G1(y1, x1)=F1(y1, x1) + G2(y2) = h1(y1) + C(x2) + G2(y2)
y1 \ x1
0
1
2
3
4
5
0



0+30+87
0+35+82
0+40+80
D. Miszczyńska, M. Miszczyński, KBO UŁ, Elementy programowania dynamicznego
9
FAZA II („do przodu”)
etap
miesiąc
1
2
3
4
styczeń
luty
marzec
kwiecień
zapas
produkcja
początkowy
0
3
0
4
1
5
3
0
popyt
3
3
3
3
lub
zapas
końcowy
0
1
3
0
Kmin = 117
etap
miesiąc
1
2
3
4
styczeń
luty
marzec
kwiecień
zapas
produkcja
początkowy
0
4
1
5
3
0
0
3
popyt
3
3
3
3
zapas
końcowy
1
3
0
0