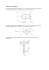Tensor momentu bezwładności

Janusz Typek
TENSOR
MOMENTU BEZWŁADNOŚCI
Szczecin, marzec 1994
Temat pracy: Tensor momentu bezwładności
Cel pracy:
Obliczenie tensora momentu bezwładności dla układu składającego
się z kilku mas punktowych oraz jego wykorzystanie do
wyznaczenia momentu bezwładności dla dowolnej osi.
Wymagania
programowe:
Obliczanie wartości własnych i wektorów własnych macierzy.
Kolejność
czynności:
1. Ustalić współrzędne przestrzenne i masy minimum czterech mas
punktowych (liczby całkowite w zakresie do kilkunastu).
Sporządzić schematyczny rysunek układu tych punktów.
2. Wyznaczyć współrzędne środka masy układu i
przetransformować do układu środka masy współrzędne
rozpatrywanych mas punktowych. Obliczyć kąty, jakie tworzą
wektory wodzące tych mas z osiami układu środka mas.
3. Obliczyć składowe tensora momentu bezwładnosci (rów.(17)).
4. Obliczyć wartości własne i wektory własne tego tensora (rów.(18)
i (19)).
5. Sporządzić rysunek przedstawiający połoŜenie osi głównych
tensora na tle mas punktowych.
6. Obliczyć długość osi elipsoidy (rów. (26)) będącej
geometrycznym przedstawieniem tensora. Naszkicować tą elipsoidę.
7. Obliczyć wartość momentu bezwładności względem dowolnej
prostej przechodzącej przez środek masy (rów. (23)).
2
Tensor momentu bezwładności Tij
r
Niech L będzie wektorem momentu pędu punktu materialnego:
r r r r
r
L = r × p = r × mv
r
gdzie r jest wektorem wodzącym punktu
r
r
r r
r = i x + j y + kz
r
zaś p jest jego pędem:
r
r
p = mv
r
W równaniu (3) m oznacza masę punktu, a v jego prędkość liniową.
JeŜeli zamiast punktu materianego mamy do czynienia z bryłą sztywną, to
r
r r
r r
L = ∑ mi ⋅ r i × v i = ρ ∫ r × v d V
i
(1)
(2)
(3).
(4)
V
gdzie ρ jest gęstością jednorodnej bryły.
r
ZałóŜmy, Ŝe bryła wykonuje ruch obrotowy wokół pewnej osi z prędkością kątową ϖ .
r r
Wiadomo, Ŝe wektory L i ϖ związane są ze sobą następującym równaniem:
r
r
(5)
L = Iˆ ⋅ ω
r r
)
Nie zawsze wektory L i ϖ leŜą na jednej prostej, zatem wielkość I nie moŜe być ani
skalarem, ani teŜ wektorem. Jest ona tensorem drugiego rzędu (bo łączy dwa wektory) i nazwana
została tensorem momentu bezwładności .
Tensor momentu bezwładności jest tensorem symetrycznym, który moŜna przedstawić w
postaci macierzy 3 na 3:
 Ixx Ixy Ixz 

) 
Ι =  Iyx Iyy Iyz 


 Izx Izy Izz 
(6)
Równanie (5) zapisane w postaci macierzowej ma postać:
 Lx   Ixx Ixy Ixz   ωx 
  
  
 Ly  =  Iyx Iyy Iyz  ⋅  ωy 
  
  
 Lz   Izx Izy Izz   ωz 
(7)
3
Niech bryła sztywna będzie złoŜona z n punktów materialnych, kaŜdy o masie mi,
umieszczonych w przestrzeni na końcach wektorów wodzących ri:
r = r ⋅ + rj ⋅ y + r ⋅
r i i xi
k zi
i
(8)
r
PoniewaŜ wektor prędkości liniowej v punktu wykonującego ruch obrotowy moŜna
przedstawić w postaci
r r r
v = ω× r
(9)
zatem równanie (4) zapiszemy następująco:
r
r r
r
L = ∑ mi ⋅ (r i × (ω × r i ))
(10)
Stosując do powyŜszego równania toŜsamość wektorową
r r r r r r rr r
a × (b × c ) = b(a ⋅ c ) − c(a ⋅ b )
(11)
i
otrzymamy:
(
)]
r
r 2 rr r
L = ∑i mi ω ⋅ri − r ω ⋅ r i i
(12)
r r
ω ⋅ r i = ωx ⋅ x + ωy ⋅ y + ωz ⋅ z
(13)
[
PoniewaŜ
dlatego równanie (12) przyjmie postać:
r
r
r
r
 i ω x ri2 + j ω y ri2 + kω z ri2 − i x (ω x x + ω y y + ω z z ) −
r
r
r
i L x + jL y + k L z = ∑ m i r
r

i
 j y(ω x x + ω y y + ω z z ) − kz(ω x x + ω y y + ω z z ) 
(14)
4
Porównując wyraŜenia występujące przy odpowiednich wersorach po obu stronach równania
(14) otrzymamy:
2
2
2
Lx = ∑i mi [ωx ri − x i (ωx xi + ωy yi + ωz zi )] = ∑i mi [ωx (ri − x i ) − ωy x i yi − ωz x i zi ]
2
2
Ly = ∑i mi [ωy ri − y (ωx x + ωy y + ωz z )] = ∑i mi [− ωx xi yi + ωy (ri − yi ) − ωz yi zi ]
2
(15)
2
2
2
Lz = ∑i mi [ωz ri − z (ωx x + ωy y + ωz z )] = ∑i mi [− zi x i ωx − ωy zi yi + ωz (ri − zi )]
Rozpisując równanie (7) dostaniemy:
Lx = Ixx ωx + Ixy ωy + Ixz ωz
Ly = Iyx ωx + Iyy ωy + Iyz ωz
Lz = Izx ωx + Izy ωy + Izz ωz
(16)
Porównanie stronami równań (15)
i (16) pozwala otrzymać ostateczne wyraŜenie na
składowe tensora momentu bezwładności:
2
2
2
Ixx = ∑i mi (ri − x i ) = ∑i mi (yi + zi )
2
2
2
Iyy = ∑i mi (x i + zi )
2
Izz = ∑i mi (x i + yi )
2
(17)
Ixy = ∑i (− mi x i yi ) = −∑i mi x i yi
Ixz = −∑i mi x i zi
Iyz = −∑i mi yi zi
PowyŜsze równania moŜna zapisać w zwięzłej postaci stosując tzw. symbol Kroneckera δkl:
1K gdy K k = l
δkl = 
0K gdy K k ≠ l
Wtedy wszystkie równania (17) zapiszą się tak:
(
)
I kl = ∑ m i r 2kl δ kl − x k x l
i
i
W powyŜszym równaniu x1=x; x2=y; x3=z.
5
Wartości własne i wektory własne tensora
Równanie na wartości własne λ tensora Tij ma postać:
T11 − λ
T21
T31
T12
T22 − λ
T32
T13
T 23 = 0
T33 − λ
(18)
Rozwiązując to równanie trzeciego stopnia otrzymujemy trzy (w ogólności róŜne) wartości
własne λ1, λ2, λ3. W przypadku tensora momentu bezwładności są to główne momenty
bezwładności względem trzech wzajemnie prostopadłych osi zwanych osiami głównymi. Osie
główne czyli wektory własne tensora wi obliczymy z równania:
 T11 − λi
T12
T13   w i1 

  
T22 − λi
T23  ⋅  w i 2  = 0
 T 21

  
T32
T33 − λi   w i 3 
 T31
(19)
dla i=1,2,3.
Geometryczna interpretacja tensora
3
γ
β
2
α
1
r
Niech wektor q tworzy z osiami układu Ox1x2x3 kąty α, β i γ. Jego składowe są zatem
r
q(q ⋅ cos(α), q ⋅ cos(β), q ⋅ cos( γ )) .MoŜna je symbolicznie zapisać jako q⋅ck, gdzie ck jest
r
odpowiednim cosinusem kierunkowym. ZałóŜmy ponadto, Ŝe wektor p powstaje skutkiem
r
działania tensora Tik na wektor q . Wtedy
pi = ∑ Tik ⋅ q ⋅ ck ≡ Tik ⋅ q ⋅ ck = q Tik ⋅ ck
k
(20)
6
gdzie zastosowano umowę sumacyjną Einsteina: jeŜeli w wyraŜeniu dany wskaźnik występuje
dwa razy (tutaj k), to naleŜy wykonać po nim sumowanie.
Przyjmijmy następującą definicję:
JeŜeli wielkość fizyczna jest określona funkcją pi=Tikqk, to tensor [Tik] ma w
r
r
obranym kierunku q wartość równą składowej p równoległej do q podzielonej przez
bezwzględną wartość q:
[T] =
r
q
p
q
(21)
r
Składowa p jest równa iloczynowi skalarnemu wektora p oraz wektora jednostkowego w
r
kierunku wektora q a ma on składowe (c1, c2, c3). Dlatego
p = ci ⋅ pi = q ⋅ ci ⋅ Tik ⋅ ck
Zgodnie z definicją (21) otrzymamy:
[T]c c c
1
2
3
=
p
q
= ci ⋅ Tik ⋅ ck
(22)
Z powyŜszego wzoru wynika, Ŝe tensor T ma w kierunku osi x1(czyli dla c1=1, c2=c3=0
wartość T11, w kierunku osi x3 wartość T33 itp.). Równanie (22) w pełnej postaci wygląda
następująco:
[T ]c c c
1
2
3
= T11 c12 + T22 c22 + T33 c32 + 2 T12 c1 c2 + 2 T23 c2 c3 + 2 T31 c3 c1
(23)
Tensor w układzie osi głównych ma zatem jedynie 3 składowe: T11,T22,T33.
Rozpatrzmy następnie równanie powierzchni drugiego stopnia:
T11 x1 + T 22 x 2 + T33 x 3 + 2 T12 x1 x 2 + 2 T 23 x 2 x 3 + 2 T31 x 3 x1 = 1
2
2
2
(24)
7
Niech punkt P leŜy na tej powierzchni, w odległości r=OP od początku okładu odniesienia i
niech cosinusy kierunkowe wektora jednostkowego prostej OP wynoszą odpowiednio ci. Zatem
xi=r⋅ci. Podstawiając te wartości do równania (24) dostaniemy:
r [T11 c1 + T22 c2 + T33 c3 + 2 T12 c1 c2 + 2 T23 c2 c3 + 2 T31 c3 c1 ] = 1
2
2
2
2
(25)
Uwzględniając (23), wzór (25) moŜna zapisać tak:
2
r [T ]c1c2c3 = 1 czyli
[T ]c c c
1
2
3
= 12
r
(26)
To ostatnie równanie moŜna zapisać w bardziej zwięzłej postaci
x i Tik x k = 1
(27)
Nazywamy je kwadryką tensora Tik.
JeŜeli własność fizyczna ma stale wartość dodatnią, jak to ma miejsce np. dla momentu
bezwładności, to kwadrykę tensora Tik stanowi elipsoida. Promień wodzący r wyprowadzony ze
środka kwadryki do dowolnego punktu na powierzchni jest równy odwrotności pierwiastka
kwadratowego własności reprezentowanej przez kwadrykę i mierzonej w kierunku promienia
wodzącego r:
1
r =
[T]rr
(28)
PRZYKŁAD
1. Współrzędne punktów (układ OXYZ) oraz ich masy:
Zakładam, Ŝe badanym układem będzie zbiór czterech mas punktowych o następujących
współrzędnych przestrzennych podanych w układzie OXYZ (patrz rysunek 1) oraz o masach mi:
Punkt
Xi
Yi
Zi
mi
P1
4
7
-1
8
P2
-3
2
4
4
P3
-7
-1
8
3
P4
1
-7
-2
7
8
2. Wyznaczenie współrzędnych (xs,ys,zs) środka masy układu:
∑ mi ⋅ X i
xs =
∑ mi ⋅ Y i
i
ys=
∑ mi
i
∑ mi
i
∑ mi ⋅ Z i
zs =
i
i
∑ mi
i
Dla układu punktów P1...P4 obliczone współrzędne środka masy wynoszą:
xs=0.272727 ys=0.545454 zs=0.818181
3. Obliczenie współrzędnych punktów w układzie środka masy (układ Oxyz)
x=X-xs
y=Y-ys
z=Z-zs
xi
yi
zi
P1
3.727272
6.454545
-1.818181
P2
-3.272727
1.454545
3.181818
P3
-7.272727
-1.545454
7.181818
P4
0.727272
-7.545454
-2.818181
Punkt
Kąty (w stopniach), jakie tworzą wektory wodzące tych punktów z osiami układu
współrzędnych Oxyz wynoszą:
9
Punkt
Ox
Oy
Oz
P1
60,9
32,7
103,7
P2
133,1
72,3
48,4
P3
134,7
98,6
46,0
P4
84,8
158,9
110,4
Obliczone one zostały z równania:
r ⋅r
⋅
+ y ⋅
+ ⋅
ri nk
= x i n kx 2 i n2 ky z2 i n kz
2
2
2
x i + yi + zi
x i + yi + zi
r
r
gdzie r i jest wektorem wodzącym wybranego punktu, a n wersorem (wektorem jednostkowym)
cos ( α ik ) =
odpowiedniej osi układu współrzędnych. Np. wersor osi Oy to wektor (0, 1, 0).
4. Obliczenie składowych tensora momentu bezwładności Iij:
Obliczenia wykonujemy w oparciu o wzory (17). Otrzymano następujące wyniki:
Ixx=1024.727
Iyy=593.6363
Izz=1063.818
Ixy=-168.7273
Ixz=266.9091
Iyz=-40.18182
PoniewaŜ tensor zawiera elementy pozadiagonalne, przyjęty układ odniesienia Oxyz nie jest
układem osi głównych tensora momentu bezwładności.
5. Obliczenie wartości własnych i wektorów własnych tensora momentu bezwładności.
Wartości własne obliczymy rozwiązując następujące równanie trzeciego stopnia względem I
(równanie (18)):
1024.727 − I
−168 .7273
266 .9091
−168 .7273
266 .9091
593.6363 − I −40 .18182 = 0
−40 .18182 1063.818 − I
Otrzymuje się następujące wartości liczbowe dla głównych momentów bezwładności:
I1=1340.41
I2=812.23
I3=529.544
r (osie główne), odpowiadające poszczególnym wartościom własnym
Trzy wektory własne w
i
obliczymy z następujących trzech równań (dla i=1,2,3) :
10
1024,727 − Ii −168.7273
266.9091   xi 

  
 −168.7273 593.6363 − Ii − 40.18182  ⋅  yi  = 0
 266.9091
− 40.18182 1063.818 − Ii   zi 

Otrzymano poniŜsze wartości liczbowe na składowe wektorów własnych:
 − 0.683918 


w1 =  0.191535 
 − 0.687807 


 0.512682 


w 2 =  − 0.287311
 − 0.58979 


 0.45832 


w 3 =  1.11561 
 − 0.145061


Punkty P1...P4 tworzą następujące kąty (w stopniach) z osiami układu osi głównych Ow1w2w3:
Obliczone zostały one z równania
r⋅r
r i wk
=
cos (δik ) =
2
2
2
2
2
2
x i + yi + zi ⋅ w kx + w ky + w kz
Punkt
Ow1
Ow2
Ow3
P1
90.5
79.8
10.2
P2
86.0
174.8
93.3
P3
91.5
150.9
119.1
P4
90.0
51.4
141.4
x i ⋅ w kx + yi ⋅ w ky + zi ⋅ w kz
2
2
2
2
2
x + yi + zi ⋅ w kx + w ky + w kz
2
i
11
6. Kwadryka tensora momentu bezwładności:
Osie elipsoidy, będącej geometrycznym przedstawieniem tensora momentu bezwładności
mają następujące długości (równanie (28)):
e1 =
1
= 0 ,027314 e2 =
I1
1
= 0 ,035088 e3 =
I2
1
= 0 ,043456
I3
7. Obliczenie momentu bezwładności względem dowolnie wybranej osi.
Rozpatrzmy dowolną prostą, której wektor jednostkowy w układzie środka masy Oxyz ma
następujące cosinusy kierunkowe:(0,45; 0,30; -0,84113). (Suma kwadratów musi być równa
jeden). Ta prosta tworzy następujące kąty z osiami głównymi (w stopniach):
α=70.6
β=39,7
γ=56,9
Moment bezwładności względem tej osi wynosi (równanie (23)):
I = (0,45) ⋅ 1340,41 + (0,30) ⋅ 812,23 + (− 0,84113) ⋅ 529,544 = 719,186
2
2
2
12