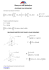Rachunek całkowy funkcji wielu zmiennych Całki podwójne i potrójne

Rachunek całkowy funkcji wielu zmiennych
Całki podwójne i potrójne
wykład z MATEMATYKI
Automatyka i Robotyka
studia stacjonarne
sem. II, rok ak. 2009/2010
Katedra Matematyki
Wydział Informatyki
Politechnika Białostocka
1
Całki podwójne
1.1
Całki podwójne po prostokącie
Definicja 1.1 (podział prostokąta).
Podziałem prostokąta P nazywamy zbiór ∆n złożony z prostokątów P1 , P2 , . . . , Pn , które całkowicie
wypełniają prostokąt P oraz mają parami rozłączne wnętrza (tzn. (intPi ) ∩ (intPj ) = ∅, dla i 6= j).
y
d
P2 P3
Pk
∆yk
P1
c
∆xk
a
b
x
Oznaczenia w definicji całki po prostokącie
∆xk , ∆yk - wymiary prostokąta Pk , gdzie 1 ¬ k ¬ n;
dk =
p
(∆xk )2 + (∆yk )2 - długość przekątnej prostokąta Pk , gdzie 1 ¬ k ¬ n;
δ(∆n ) = max dk - średnica podziału ∆n ;
1¬k¬n
A = {A1 (x∗1 , y1∗ ), A2 (x∗2 , y2∗ ), . . . , An (x∗n , yn∗ )} , gdzie Ak (x∗k , yk∗ ) ∈ Pk dla 1 ¬ k ¬ n, A - zbiór
punktów pośrednich podziału ∆n .
Definicja 1.2 (Suma całkowa funkcji po prostokącie).
Niech funkcja f będzie ograniczona na prostokącie P oraz niech ∆n będzie podziałem tego prostokąta, a
A zbiorem punktów pośrednich.
1
Automatyka i Robotyka
sem II, 2009/2010
Katedra Matematyki
MATEMATYKA - wykład
Sumą całkową funkcji f odpowiadającą podziałowi ∆n oraz punktom pośrednim A nazywamy
liczbę
n
X
f (x∗k , yk∗ ) · (∆xk ) · (∆yk ) .
k=1
Uwaga 1. Suma całkowa jest przybliżeniem objętości bryły ograniczonej wykresem funkcji z = f (x, y) > 0
leżącym nad prostokątem P oraz płaszczyzną XOY przez objętości prostopadłościanów o podstawach Pk i
wysokościach f (x∗k , yk∗ ), dla 1 6 k 6 n.
Definicja 1.3. Niech funkcja f będzie ograniczona na prostokącie P .
Całkę podwójną funkcji f po prostokącie P definiujemy wzorem
x
def
f (x, y)dxdy =
P
lim
δ(∆n )→0
n
X
f (x∗k , yk∗ ) · (∆xk ) · (∆yk ) ,
k=1
o ile granica po prawej stronie znaku równości jest właściwa i nie zależy od sposobu podziału ∆n prostokąta
P ani od sposobu wyboru punktów pośrednich A.
Mówimy wtedy, że funkcja f jest całkowalna na prostokącie P .
Uwaga 2. Całkę podwójną z funkcji f po prostokącie P oznaczamy też symbolem:
x
f (x, y)dP .
P
Całka podwójna po prostokącie jest uogólnieniem całki z funkcji jednej zmiennej po przedziale.
Twierdzenie 1.4 (o całkowalności funkcji ciągłych).
Funkcja ciągła na prostokącie jest na nim całkowalna.
Twierdzenie 1.5 (o liniowości całki).
Niech funkcje f i g będą całkowalne na prostokącie P oraz niech α, β ∈ R. Wtedy
x
x
x
[αf (x, y) + βg(x, y)] dxdy = α f (x, y)dxdy + β
g(x, y)dxdy .
P
P
P
Twierdzenie 1.6 (o addytywności całki względem obszaru całkowania).
Jeżeli funkcja f jest całkowalna na prostokącie P , to dla dowolnego podziału tego prostokąta na prostokąty
P1 i P2 o rozłącznych wnętrzach zachodzi równość
x
x
x
f (x, y)dxdy =
f (x, y)dxdy +
f (x, y)dxdy .
P
P1
P2
Twierdzenie 1.7 (o zamianie całki podwójnej na całkę iterowaną).
Jeżeli funkcja f jest całkowalna na prostokącie P = ha, bi × hc, di, to
x
P
f (x, y)dxdy =
Zb Zd
a
f (x, y)dy dx =
c
2
Zd Zb
c
a
f (x, y)dx dy .
Automatyka i Robotyka
sem II, 2009/2010
Katedra Matematyki
MATEMATYKA - wykład
Uwaga 3. Całkę iterowaną
Zb Zd
f (x, y)dy dx
Zb
Zd
a
c
możemy zapisywać umownie
dx
a
f (x, y)dy .
c
Podobną umowę możemy przyjąć dla drugiej całki iterowanej, tzn.
Zd Zb
c
π π
Przykład 1.8. Niech P = − ,
4 4
x
Obliczyć
sin(x + y)dxdy .
f (x, y)dx dy =
a
Zd
c
dy
Zb
f (x, y)dx .
a
π
× 0,
.
4
P
Twierdzenie 1.9 (całka podwójna z funkcji o rozdzielonych zmiennych).
Jeżeli funkcja f jest funkcją postaci f (x, y) = g(x) · h(y), gdzie g i h są ciągłe odpowiednio na przedziałach
ha, bi i hc, di, to
x
P

g(x) · h(y)dxdy = 
Zb
a
 
g(x)dx · 
Zd
c

h(y)dy  .
Przykład 1.10. Niech P = h0, 1i × h−1, 1i.
x
Obliczyć
ex+y dxdy .
P
1.2
Całki podwójne po obszarach normalnych
Niech f będzie funkcją określoną i ograniczoną w obszarze ograniczonym D ⊂ R2 oraz niech P będzie
dowolnym prostokątem zawierającym obszar P .
Ponadto niech f ∗ oznacza rozszerzenie funkcji f na P określone wzorem:
def
f ∗ (x, y) =

f (x, y),
0,
3
dla (x, y) ∈ D,
dla (x, y) ∈ P \ D.
Automatyka i Robotyka
sem II, 2009/2010
Katedra Matematyki
MATEMATYKA - wykład
Definicja 1.11. Całkę podwójną funkcji f po obszarze D definiujemy wzorem:
x
def
f (x, y)dxdy =
D
x
f ∗ (x, y)dxdy ,
P
o ile całka po prawej stronie znaku równości istnieje.
Mówimy wtedy, że funkcja f jest całkowana w obszarze D .
s
Uwaga 4. Całka f ∗ (x, y)dxdy nie zależy od wyboru prostokąta P .
P
Definicja 1.12 (Obszary normalne względem osi układu).
Obszar domknięty D nazywamy obszarem normalnym względem osi OX, jeżeli można go zapisać w postaci:
D = {(x, y) : a 6 x 6 b ∧ g(x) 6 y 6 h(x)} ,
gdzie funkcje g i h są ciągłe na ha, bi, przy czym g(x) < h(x) dla x ∈ (a, b).
Obszar domknięty D nazywamy obszarem normalnym względem osi OY , jeżeli można go zapisać w postaci:
D = {(x, y) : c 6 y 6 d ∧ p(y) 6 x 6 q(y)} ,
gdzie funkcje p i q są ciągłe na hc, di, przy czym p(y) < q(y) dla y ∈ (c, d).
Przykład 1.13.
Obszar D ograniczony krzywymi y = 0, x = 2 i y = x
2
jest obszarem normalnym zarówno względem
osi OX jak również względem osi OY .
Obszar D ograniczony krzywymi y = −1, y = 1, x = 2 − p1 − y
normalnym względem osi OY .
4
2
ix=
p
1 − y 2 − 1 jest obszarem
Automatyka i Robotyka
sem II, 2009/2010
Katedra Matematyki
MATEMATYKA - wykład
Twierdzenie 1.14 (Całki iterowane po obszarach normalnych).
Jeżeli funkcja f jest ciągła na obszarze domkniętym
D = {(x, y) : a 6 x 6 b ∧ g(x) 6 y 6 h(x)}
normalnym względem osi OX, to
x
f (x, y)dxdy =
D
Zb
a
h(x)
Z
f (x, y)dy dx .
g(x)
Jeżeli funkcja f jest ciągła na obszarze domkniętym
D = {(x, y) : c 6 y 6 d ∧ p(y) 6 x 6 q(y)}
normalnym względem osi OY , to
x
D
f (x, y)dxdy =
Zd
c
q(y)
Z
f (x, y)dx dy .
p(y)
Przykład 1.15. Niech D = {(x, y) : y > x ∧ y 6 3x − x2 }.
x
Obliczyć
x2 − xy dxdy .
D
Definicja 1.16 (obszar regularny na płaszczyźnie).
Sumę skończonej liczby obszarów normalnych względem osi układu o parami rozłącznych wnętrzach nazywamy obszarem regularnym na płaszczyźnie.
Twierdzenie 1.17 (całka po obszarze regularnym).
Niech obszar regularny D = D1 ∪ D2 ∪ . . . ∪ Dn i intDi ∩ intDj = ∅, dla i 6= j oraz niech funkcja f będzie
całkowalna na D. Wtedy
x
x
x
x
f (x, y)dxdy =
f (x, y)dxdy +
f (x, y)dxdy + . . . +
f (x, y)dxdy.
D
D1
D2
Przykład 1.18. Niech D = {(x, y) : xy 6 1 ∧ |x − y| 6 1}.
x
Obliczyć
xydxdy .
D
5
Dn
Automatyka i Robotyka
sem II, 2009/2010
MATEMATYKA - wykład
Katedra Matematyki
Definicja 1.19 (wartość średnia funkcji f w obszarze D).
Wartością średnią funkcji f na obszarze D nazywamy liczbę
def
fśr =
1 x
f (x, y)dxdy ,
|D|
D
gdzie |D| oznacza pole obszaru D.
Uwaga 5. Wartość średnia funkcji f w obszarze D jest równa wysokości walca o podstawie D, który ma
tę samą objętość co bryła V .
Przykład 1.20. Wysokość nad poziomem
morza pewnego terenu jest opisana wzorem w(x, y) = 20 +
π π
. Oblicz średnie wzniesienie tego terenu.
sin x cos 2y, gdzie (x, y) ∈ h0, πi × − ,
2 2
Twierdzenie 1.21. Jeżeli funkcja f jest ciągła na obszarze normalnym D, to w tym obszarze istnieje
punkt (x0 , y0 ), taki że
fśr = f (x0 , y0 ).
6
Automatyka i Robotyka
sem II, 2009/2010
1.3
MATEMATYKA - wykład
Katedra Matematyki
Zamiana zmiennych w całkach podwójnych
Definicja 1.22 (przekształcenia obszarów na płaszczyźnie).
Niech ∆ ⊂ R2 i D ⊂ R2 będą obszarami odpowiednio na płaszczyznach U OV i XOY .
Przekształceniem obszaru ∆ w obszar D nazywamy funkcję F : ∆ → D określoną wzorem
(x, y) = F(u, v) = (ϕ(u, v), ψ(u, v)) ,
gdzie (u, v) ∈ ∆.
def
F(∆) = {(x, y) : x = ϕ(u, v) ∧ y = ψ(u, v) ∧ (u, v) ∈ ∆} - obraz zbioru ∆.
Jeżeli funkcje ϕ, ψ są ciągłe na obszarze ∆, to przekształcenie F nazywamy ciągłym.
Jeżeli różnym punktom obszaru ∆ odpowiadają różne punkty jego obrazu D, to przekształcenie F nazywamy różnowartościowym.
∂ϕ (u, v)
∂u
JF (u, v) = ∂ψ (u, v)
∂u
∂ϕ
∂v (u, v)
∂ψ
∂v (u, v)
- jakobian przekształcenia F.
Twierdzenie 1.23. Obraz obszaru przy przekształceniu ciągłym i różnowartościowym jest również obszarem.
Przykład 1.24. Niech F (u, v) = (u + v, u − v) i ∆ = {(u, v) : 0 6 u 6 1 ∧ 2 6 v 6 4}.
Twierdzenie 1.25 (o zamianie zmiennych w całkach podwójnych). Niech
przekształcenie F odwzorowuje różnowartościowo wnętrze obszaru regularnego ∆ na wnętrze obszaru
regularnego D,
funkcje ϕ, ψ mają ciągłe pochodne cząstkowe rzędu pierwszego na pewnym zbiorze otwartym zawierającym obszar ∆,
funkcja f będzie ciągła na obszarze D,
J (u, v) 6= 0, dla (u, v) ∈ int∆.
F
Wtedy
x
D
f (x, y)dxdy =
x
f (ϕ(u, v), ψ(u, v)) · |JF (u, v)| dudv .
∆
Przykład 1.26. Niech D będzie obszarem ograniczonym krzywymi 2x + y = 2, 2x + y = 3, x − y = −1
i x − y = 1.
x
Obliczyć
(x + y)dxdy .
D
7
Automatyka i Robotyka
sem II, 2009/2010
1.4
MATEMATYKA - wykład
Katedra Matematyki
Współrzędne biegunowe w całkach podwójnych
Położenie punktu A(x, y) na płaszczyźnie można opisać parą liczb (ϕ, ̺), gdzie:
ϕ – oznacza miara kąta między dodatnią częścią osi OX a promieniem wodzącym punktu A, 0 ¬
ϕ < 2π lub −π < ϕ 6 π,
̺ – oznacza odległość punktu A od początku układu współrzędnych, 0 6 ̺ < ∞.
Parę liczb (ϕ, ̺) nazywamy współrzędnymi biegunowymi punktu płaszczyzny .
Zależność między współrzędnymi biegunowymi i kartezjańskimi

x = ̺ cos ϕ
B:
y = ̺ sin ϕ
Przekształcenie B, które każdemu punktowi (ϕ, ̺) przyporządkowuje punkt (x, y) określony powyższymi
wzorami, nazywamy przekształceniem biegunowym.
Jakobian przekształcenia biegunowego JB = ̺.
Twierdzenie 1.27 (współrzędne biegunowe w całce podwójnej). Niech
obszar ∆ we współrzędnych biegunowych będzie obszarem regularnym
funkcja f będzie ciągła na obszarze D, który jest obrazem obszaru ∆ przy przekształceniu biegunowym, tzn. D = B(∆).
Wtedy
x
D
f (x, y)dxdy =
x
f (̺ cos ϕ, ̺ sin ϕ) · ̺ d̺dϕ .
∆
Przykład 1.28. Niech D będzie obszarem ograniczonym krzywą x2 + y 2 = 1.
x
Obliczyć
ln(1 + x2 + y 2 )dxdy .
D
Przykład 1.29. Niech D będzie obszarem ograniczonym krzywą x2 + y 2 = 2.
x
2
2
Obliczyć
e−(x +y ) dxdy .
D
8
Automatyka i Robotyka
sem II, 2009/2010
1.5
Katedra Matematyki
MATEMATYKA - wykład
Zastosowania całek podwójnych w geometrii
Pole obszaru
Pole obszaru regularnego D ⊂ R2 wyraża się wzorem:
|D| =
x
dxdy .
D
Objętość bryły
Objętość bryły V położonej nad obszarem regularnym D ⊂ R2 i ograniczonej z dołu i z góry odpowiednio
wykresami funkcji ciągłych z = d(x, y) i z = g(x, y) wyraża się wzorem:
|V | =
x
[g(x, y) − d(x, y)] dxdy .
D
Pole płata
Pole płata Σ, który jest wykresem funkcji z = f (x, y), gdzie (x, y) ∈ D wyraża się wzorem:
|Σ| =
x
D
s
1+
∂f
∂x
2
+
∂f
∂y
2
dxdy .
Przykład 1.30.
Oblicz pole obszaru ograniczonego krzywymi x = y 2 i x = 1.
Oblicz objętość bryły ograniczonej wskazanymi powierzchniami x + z
2
Oblicz pole części powierzchni z = px + y
2
2
2
= 4, y 2 + z 2 = 4 i x, y, z > 0.
odciętych płaszczyznami z = 1 i z = 2.
9
Automatyka i Robotyka
sem II, 2009/2010
1.6
MATEMATYKA - wykład
Katedra Matematyki
Zastosowania całek podwójnych w mechanice
Masa obszaru
Masa obszaru D ⊂ R2 o gęstości powierzchniowej masy ρ wyraża się wzorem:
M=
x
ρ(x, y)dxdy .
D
Momenty statyczne
Momenty statyczne względem osi OX i OY obszaru D ⊂ R2 o gęstości powierzchniowej masy ρ wyrażają
się wzorami:
x
M Sx =
yρ(x, y)dxdy ,
D
M Sy =
x
xρ(x, y)dxdy .
D
Współrzędne środka masy
Współrzędne środka masy obszaru D ⊂ R2 o gęstości powierzchniowej masy ρ wyrażają się wzorami:
xC =
M Sy
,
M
yC =
M Sx
.
M
Momenty bezwładności
Momenty bezwładności względem osi OX, OY obszaru D ⊂ R2 o gęstości powierzchniowej masy ρ
wyrażają się wzorami:
x
Ix =
y 2 ̺(x, y)dxdy ,
D
Iy =
x
x2 ̺(x, y)dxdy .
D
Moment bezwładności względem punktu O(0, 0) obszaru D ⊂ R2 o gęstości powierzchniowej masy ρ
wyraża się wzorem:
x
IO =
(x2 + y 2 )̺(x, y)dxdy .
D
10
Automatyka i Robotyka
sem II, 2009/2010
2
MATEMATYKA - wykład
Katedra Matematyki
Całki potrójne
2.1
Całki potrójne po prostopadłościanie
Rozważmy prostopadłościan P określony w przestrzeni układu OXY Z nierównościami:
P : a¬ x ¬b∧c¬ y ¬ d∧p ¬ z ¬ q
oraz funkcję trzech zmiennych f (x, y, z) określoną i ograniczoną w tym prostopadłościanie.
Definicja 2.1. Podziałem prostopadłościanu P nazywamy zbiór ∆n złożony z prostopadłościanów
P1 , P2 , . . . , Pn , które całkowicie wypełniają P oraz mają parami rozłączne wnętrza (tzn. (intPi )∩(intPj ) =
∅, dla i 6= j).
Oznaczenia stosowane w definicji całki po prostopadłościanie:
• ∆xk , ∆yk , ∆zk - wymiary prostopadłościanu Pk , gdzie 1 ¬ k ¬ n;
• dk =
p
(∆xk )2 + (∆yk )2 + (∆zk )2 - długość przekątnej prostopadłościanu Pk , gdzie 1 ¬ k ¬ n;
• δn = max dk - średnica podziału ∆n ;
1¬k¬n
• A = {A1 (x∗1 , y1∗ , z1∗ ), A2 (x∗2 , y2∗ , z2∗ ), . . . , An (x∗n , yn∗ , zn∗ )}, gdzie Ak (x∗k , yk∗ , zk∗ ) ∈ Pk dla 1 ¬ k ¬ n, A zbiór punktów pośrednich podziału ∆n .
Definicja 2.2 (suma całkowa funkcji po prostopadłościanie).
Niech funkcja f będzie ograniczona na prostopadłościanie P oraz niech ∆n będzie podziałem tego prostopadłościanu, a A zbiorem punktów pośrednich.
Sumą całkową funkcji f odpowiadającą podziałowi ∆n oraz punktom pośrednim A nazywamy
liczbę
n
X
f (x∗k , yk∗ , zk∗ ) · (∆xk ) · (∆yk ) · (∆zk ) .
k=1
Definicja 2.3 (całkowa potrójna po prostopadłościanie).
Niech funkcja f będzie ograniczona na prostopadłościanie P .
Całkę potrójną funkcji f po prostopadłościanie P definiujemy wzorem
y
P
def
f (x, y, z)dxdydz = lim
δn →0
n
X
f (x∗k , yk∗ , zk∗ ) · (∆xk ) · (∆yk ) · (∆zk ) ,
k=1
o ile granica po prawej stronie znaku równości jest właściwa i nie zależy od sposobu podziału ∆n prostopadłościanu P ani od sposobu wyboru punktów pośrednich A.
Mówimy wtedy, że funkcja f jest całkowalna na prostopadłościanie P .
11
Automatyka i Robotyka
sem II, 2009/2010
Katedra Matematyki
MATEMATYKA - wykład
Uwaga 6. Całkę potrójną z funkcji f po prostopadłościanie P oznaczamy też symbolem:
y
f (x, y, z)dV .
P
Twierdzenie 2.4. Funkcja ciągła na prostopadłościanie jest na nim całkowalna.
Twierdzenie 2.5 (o liniowości całki).
Niech funkcje f i g będą całkowalne na prostopadłościanie P oraz niech α, β ∈ R. Wtedy
y
(αf (x, y, z) + βg(x, y, z)) dxdydz = α
y
P
f (x, y, z)dxdydz + β
P
y
g(x, y, z)dxdydz .
P
Twierdzenie 2.6 (o addytywności względem obszaru całkowania).
Jeżeli funkcja f jest całkowalna na prostopadłościanie P , to dla dowolnego podziału tego prostopadłościanu
na prostopadłościany P1 i P2 o rozłącznych wnętrzach zachodzi równość
y
y
f (x, y, z)dxdydz =
P
f (x, y, z)dxdydz +
P1
y
f (x, y, z)dxdydz .
P2
Twierdzenie 2.7 (o zamianie całki potrójnej na całkę iterowaną).
Jeżeli funkcja f jest całkowalna na prostopadłościanie P = ha, bi × hc, di × hp, qi, to
y
ha,bi×hc,di×hp,qi
 
 
Zb Zd Zq

 f (x, y, z)dz  dy dx .
f (x, y, z)dxdydz =


a
c
p
Uwaga 7. Powyższe twierdzenie będzie prawdziwe także wtedy, gdy po prawej stronie równości napiszemy
dowolną całkę iterowaną (jest sześć rodzajów całek iterowanych). Całkę iterowaną
 
 
Zb Zd Zq

 f (x, y, z)dz  dy dx


a
możemy zapisywać umownie
c
Zb
a
p
dx
Zd
c
dy
Zq
f (x, y, z)dz.
p
Podobną umowę możemy przyjąć dla pozostałych całek iterowanych.
Przykład 2.8. Niech P = h−1, 1i × h0, 1i × h2, 4i.
y
Oblicz
(2x − y + 3z)dxdydz .
P
12
Automatyka i Robotyka
sem II, 2009/2010
2.2
MATEMATYKA - wykład
Katedra Matematyki
Całki potrójne po obszarach normalnych
Definicja 2.9 (całka potrójna po obszarze).
Niech f będzie funkcją ograniczoną na obszarze ograniczonym V ⊂ R3 oraz niech P będzie dowolnym prostopadłościanem zawierającym obszar V . Ponadto niech f ∗ oznacza rozszerzenie funkcji f na P określone
wzorem:

def
f ∗ (x, y, z) =
dla (x, y, z) ∈ V ,
f (x, y, z),
dla (x, y, z) ∈ P \ V .
0,
Całkę potrójną funkcji f po obszarze V definiujemy wzorem:
y
def
f (x, y, z)dxdydz =
y
V
f ∗ (x, y, z)dxdydz ,
P
o ile całka po prawej stronie znaku równości istnieje.
Mówimy wtedy, że funkcja f jest całkowana w obszarze V
t ∗
Uwaga 8. Całka
f (x, y, z)dxdydz nie zależy od wyboru prostopadłościanu P .
P
Definicja 2.10 (Obszary normalne względem płaszczyzn układu współrzędnych).
1 Obszar domknięty V nazywamy obszarem normalnym względem płaszczyzny XOY , jeżeli można go zapisać w postaci:
V = {(x, y, z) : (x, y) ∈ Dxy ∧ g(x, y) ¬ z ¬ h(x, y)} ,
gdzie Dxy jest obszarem normalnym na płaszczyźnie XOY , a funkcje g i h są ciągłe na Dxy , przy
czym g(x, y) < h(x, y) dla punktów (x, y) należących do wnętrza obszaru Dxy (∗) .
2 Obszar domknięty V nazywamy obszarem normalnym względem płaszczyzny XOZ, jeżeli można go zapisać w postaci:
V = {(x, y, z) : (x, z) ∈ Dxz ∧ p(x, z) ¬ y ¬ q(x, z)} ,
gdzie Dxz jest obszarem normalnym na płaszczyźnie XOZ, a funkcje p i q są ciągłe na Dxz , przy
czym p(x, z) < q(x, z) dla punktów (x, z) należących do wnętrza obszaru Dxz (∗) .
3 Obszar domknięty V nazywamy obszarem normalnym względem płaszczyzny Y OZ, jeżeli można go zapisać w postaci:
V = {(x, y, z) : (y, z) ∈ Dyz ∧ r(y, z) ¬ x ¬ s(y, z)} ,
gdzie Dyz jest obszarem normalnym na płaszczyźnie Y OZ, a funkcje r i s są ciągłe na Dyz , przy
czym r(y, z) < s(y, z) dla punktów (y, z) należących do wnętrza obszaru Dyz (∗) .
(∗)
Dxy - rzut obszaru V na płaszczyznę XOY .
Dxz - rzut obszaru V na płaszczyznę XOZ.
(∗)
Dyz - rzut obszaru V na płaszczyznę Y OZ.
(∗)
13
Automatyka i Robotyka
sem II, 2009/2010
Katedra Matematyki
MATEMATYKA - wykład
Twierdzenie 2.11. Jeżeli funkcja f jest ciągła na obszarze domkniętym
V = {(x, y, z) : (x, y) ∈ Dxy ∧ g(x, y) ¬ z ¬ h(x, y)}
normalnym względem płaszczyzny XOY , gdzie funkcje g i h są ciągłe na Dxy , to
y
f (x, y, z)dxdydz =
V
x
Dxy




h(x,y)
Z
f (x, y, z)dz  dxdy .
g(x,y)

Uwaga 9. Prawdziwe są analogiczne wzory z całkami iterowanymi po obszarach normalnych względem
pozostałych płaszczyzn układu. Jeżeli obszar V normalny względem płaszczyzny XOY można zapisać w
postaci:
V :
to zachodzi równość
y
V



a¬x¬b
.
g̃(x) ¬ y ¬ h̃(x)


g(x, y) ¬ z ¬ h(x, y),
f (x, y, z)dxdydz =

 

h̃(x) h(x,y)

Zb 
Z
Z



f (x, y, z)dz  dy dx





a
g̃(x)
g(x,y)
||
Zb
dx
a
h̃(x)
Z
g̃(x)
dy
h(x,y)
Z
f (x, y, z)dz.
g(x,y)
Przykład 2.12. Niech V będzie obszarem ograniczonym powierzchniami z = y 2 − x2 , z = 0, x = 0,
y = 1 i y = x.
y
Oblicz
(x2 + y 2 )dxdydz .
V
Przykład 2.13. Niech V będzie obszarem ograniczonym powierzchniami z = y, z = 0 i y = 1 − x2 .
y
Oblicz
ydxdydz .
V
14
Automatyka i Robotyka
sem II, 2009/2010
Katedra Matematyki
MATEMATYKA - wykład
Definicja 2.14. Sumę skończonej liczby obszarów normalnych względem płaszczyzn układu o parami
rozłącznych wnętrzach nazywamy obszarem regularnym w przestrzeni.
Twierdzenie 2.15. Niech obszar regularny V = V1 ∪ V2 ∪ . . . ∪ Vn oraz intVi ∩ intVj = ∅, dla i 6= j oraz
niech funkcja f będzie całkowalna na V . Wtedy
y
V
f (x, y, z)dxdydz =
y
f (x, y, z)dxdydz +
V1
y
f (x, y, z)dxdydz + . . . +
V2
y
f (x, y, z)dxdydz .
Vn
Uwaga 10. Całki po obszarach regularnych mają te same własności co całki po prostopadłościanach, tzn.
liniowość, addytywność względem obszaru całkowania.
Definicja 2.16. Wartością średnią funkcji f na obszarze V nazywamy liczbę
fśr :=
1 y
f (x, y, z)dxdydz ,
|V |
V
gdzie |V | oznacza objętość obszaru V .
Twierdzenie 2.17. Jeżeli funkcja f jest ciągła na obszarze normalnym V , to w tym obszarze istnieje
punkt (x0 , y0 , z0 ), taki że
fśr = f (x0 , y0 , z0 ).
Przykład 2.18. Niech V = {(x, y, z) : 0 6 x 6 1 ∧ 0 6 y 6 x ∧ 0 6 z 6 x + y}.
Oblicz wartość średnią funkcji f (x, y, z) = x + y + z .
Przykład 2.19. W punkcie (x, y, z) prostopadłościanu V = {(x, y, z) : 0 6 x 6 1∧0 6 y 6 2∧0 6 z 6 3}.
temperatura określona jest wzorem
T (x, y, z) = y sin πx + z .
Oblicz średnią temperaturę w tym prostopadłościanie.
15
Automatyka i Robotyka
sem II, 2009/2010
2.3
MATEMATYKA - wykład
Katedra Matematyki
Zamiana zmiennych w całkach potrójnych
Niech Ω i V będą obszarami odpowiednio w przestrzeniach U OV W i XOY Z.
Przekształceniem obszaru Ω w obszar V nazywamy funkcję F : Ω → V określoną wzorem
(x, y, z) = F(u, v, w) = (ϕ(u, v, w), ψ(u, v, w), χ(u, v, w)) ,
gdzie (u, v, w) ∈ Ω.
def
F(Ω) = {(x, y, z) : x = ϕ(u, v, w) ∧ y = ψ(u, v, w) ∧ z = χ(u, v, w) ∧ (u, v, w) ∈ Ω} - obraz zbioru Ω.
Jeżeli funkcje ϕ, ψ, χ są ciągłe na obszarze Ω, to przekształcenie F nazywamy ciągłym.
Jeżeli różnym punktom obszaru Ω odpowiadają różne punkty jego obrazu, to przekształcenie F nazywamy
różnowartościowym.
∂ϕ
(u, v, w)
∂u
JF (u, v, w) = ∂ψ
(u, v, w)
∂u
∂χ
(u, v, w)
∂u
∂ϕ
∂v (u, v, w)
∂ψ
∂v (u, v, w)
∂χ
∂v (u, v, w)
∂ϕ
∂w (u, v, w) ∂ψ
(u,
v,
w)
∂w
∂χ
∂w (u, v, w)
- jakobian przekształcenia F
Stwierdzenie 2.20. Obraz obszaru przy przekształceniu ciągłym i różnowartościowym jest również obszarem.
Twierdzenie 2.21 (o zamianie zmiennych w całce potrójnej).
Niech
przekształcenie F odwzorowuje różnowartościowo wnętrze obszaru regularnego Ω na wnętrze obszaru
regularnego V ,
funkcje ϕ, ψ, χ mają ciągłe pochodne cząstkowe rzędu pierwszego na pewnym zbiorze otwartym zawierającym obszar Ω,
funkcja f będzie ciągła na obszarze V ,
J (u, v, w) 6= 0, dla (u, v, w) ∈ intΩ.
F
Wtedy
y
f (x, y, z)dxdydz =
V
y
f (ϕ(u, v, w), ψ(u, v, w), χ(u, v, w)) · |JF (u, v, w)| dudvdz .
Ω
Współrzędne walcowe w całkach potrójnych
Położenie punktu A(x, y, z) w przestrzeni można opisać trójką liczb (ϕ, ̺, h), gdzie:
ϕ – oznacza miara kąta między rzutem promienia wodzącego punktu A na płaszczyznę XOY , a
dodatnią częścią osi OX, 0 ¬ ϕ < 2π lub −π < ϕ ¬ π,
̺ – oznacza odległość rzutu punktu A na płaszczyznę XOY od początku układu współrzędnych,
0 ¬ ̺ < ∞,
h – oznacza odległość (dodatnia dla z > 0 i ujemną dla z < 0) punktu P od płaszczyzny XOY ,
−∞ < h < ∞.
16
Automatyka i Robotyka
sem II, 2009/2010
MATEMATYKA - wykład
Katedra Matematyki
Trójkę liczb (ϕ, ̺, h) nazywamy współrzędnymi walcowymi punktu przestrzeni .
Zależność między współrzędnymi walcowymi i kartezjańskimi:
W:



x = ̺ cos ϕ


y = ̺ sin ϕ



z = h
Przekształcenie W, które każdemu punktowi (ϕ, ̺, h) przyporządkowuje punkt (x, y, z) określony powyższymi wzorami, nazywamy przekształceniem walcowym.
Jakobian przekształcenia walcowego JW = ̺.
Twierdzenie 2.22. Niech
obszar Ω we współrzędnych walcowych będzie obszarem normalnym
funkcja f będzie ciągła na obszarze V , który jest obrazem obszaru Ω przy przekształceniu walcowym,
tzn. V = W(Ω).
Wtedy
y
V
f (x, y, z)dxdydz =
y
f (̺ cos ϕ, ̺ sin ϕ, h) · ̺ dhd̺dϕ .
Ω
Przykład 2.23. Niech V będzie obszarem ograniczonym paraboloidą z = 9 − x2 − y 2 i płaszczyzną z = 0.
y
Oblicz
x2 dxdydz .
V
p
Przykład 2.24. Niech V będzie obszarem ograniczonym powierzchnią stożka z = 2 x2 + y 2 i płaszczyzną z = 8.
y
Oblicz
(x2 + y 2 )dxdydz .
V
17
Automatyka i Robotyka
sem II, 2009/2010
Katedra Matematyki
MATEMATYKA - wykład
Współrzędne sferyczne w całkach potrójnych
Położenie punktu A(x, y, z) w przestrzeni można opisać trójką liczb (ϕ, ψ, ̺), gdzie:
• ϕ – oznacza miara kąta między rzutem promienia wodzącego punktu A na płaszczyznę XOY , a
dodatnią częścią osi OX, 0 ¬ ϕ < 2π lub −π < ϕ ¬ π,
• ψ – oznacza miara kąta między promieniem wodzącym punktu A, płaszczyzną XOY , − π2 ¬ ψ ¬ π2 ,
• ̺ – oznacza odległość punktu A od początku układu współrzędnych, 0 ¬ ̺ < ∞.
Trójkę liczb (ϕ, ψ, ̺) nazywamy współrzędnymi sferycznymi punktu przestrzeni .
Zależność między współrzędnymi sferycznymi i kartezjańskimi:
S:



x = ̺ cos ϕ cos ψ


y = ̺ sin ϕ cos ψ



z = ̺ sin ψ
Przekształcenie S, które każdemu punktowi (ϕ, ψ, ̺) przyporządkowuje punkt (x, y, z) określony powyższymi wzorami, nazywamy przekształceniem sferycznym.
Jakobian przekształcenia sferycznego JW = ̺2 cos ψ.
Twierdzenie 2.25. Niech
obszar Ω we współrzędnych biegunowych będzie obszarem normalnym
funkcja f będzie ciągła na obszarze V , który jest obrazem obszaru Ω przy przekształceniu sferycznym,
tzn. V = S(Ω).
Wtedy
y
V
f (x, y, z)dxdydz =
y
f (̺ cos ϕ cos ψ, ̺ sin ϕ cos ψ, ̺ sin ψ) · ̺2 · cos ψ d̺dψdϕ .
Ω
Przykład 2.26. Niech V będzie obszarem ograniczonym półsferą z =
Oblicz
y q
z 2 x2 + y 2 + z 2 dxdydz .
V
18
p
4 − x2 − y 2 i płaszczyzną z = 0.
Automatyka i Robotyka
sem II, 2009/2010
Katedra Matematyki
MATEMATYKA - wykład
p
Przykład 2.27. Niech V będzie obszarem ograniczonym powierzchnią z = 2 1 − x2 − y 2 i płaszczyzną
1
z = . Oblicz
2
y
dxdydz
.
x2 + y 2 + z 2
V
19
Automatyka i Robotyka
sem II, 2009/2010
Katedra Matematyki
MATEMATYKA - wykład
Zastosowania całek potrójnych w geometrii i mechanice
Objętość obszaru
Objętość obszaru V ⊂ R3 wyraża się wzorem:
y
|V | =
dxdydz .
V
Masa obszaru
Masa obszaru V ⊂ R3 o gęstości objętościowej masy ̺ wyraża się wzorem:
M=
y
̺(x, y, z)dxdydz .
V
Momenty statyczne
Momenty statyczne względem płaszczyzn układu współrzędnych obszaru V ⊂ R3 o gęstości objętościowej
masy ̺ wyrażają się wzorami:
y
M Sxy =
z̺(x, y, z)dxdydz ,
V
M Sxz =
y
y̺(x, y, z)dxdydz ,
V
M Syz =
y
x̺(x, y, z)dxdydz .
V
Współrzędne środka masy
Współrzędne środka masy obszaru V ⊂ R3 o gęstości objętościowej masy ̺ wyrażają się wzorami:
xC =
M Syz
,
M
yC =
M Sxz
,
M
zC =
M Sxy
.
M
Momenty bezwładności
Momenty bezwładności względem osi OX, OY , OZ obszaru V ⊂ R3 o gęstości objętościowej masy ̺
wyrażają się wzorami:
y
Ix =
(y 2 + z 2 )̺(x, y, z)dxdydz ,
V
Iy =
y
(x2 + z 2 )̺(x, y, z)dxdydz ,
V
Iz =
y
(x2 + y 2 )̺(x, y, z)dxdydz .
V
Moment bezwładności względem punktu O(0, 0, 0) obszaru V ⊂ R3 o gęstości objętościowej masy ̺ wyraża
się wzorem:
y
IO =
(x2 + y 2 + z 2 )̺(x, y, z)dxdydz .
V
20