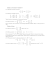Pochodne i całki, macierze i wyznaczniki

Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Pochodne i całki, macierze i wyznaczniki
Stanisław Jaworski
Katedra Ekonometrii i Statystyki
Zakład Statystyki
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Definicja
Własności
Przykłady
Niech f (x) oznacza funkcję ograniczoną na przedziale domkniętym
< a, b >.
Niech P1 , P2 , . . . , Pm , . . . będą różnym podziałami przedziału
< a, b >. Podział Pm jest osiągnięty przy pomocy nm − 1 liczb
x1 , x2 , . . . , xnm −1 , przy czym
a = x0 < x1 < x2 < . . . < xnm −1 < xnm = b.
Przedziały < xi−1 , xi >, gdzie i = 1, 2, . . . , nm , nazywamy
przedziałami cząstkowymi podziału Pm . Długości ich xi − xi−1
będziemy oznaczali przez ∆xi
Niech δm = max ∆xi oraz
i
Sm =
nm
X
f (ci )∆xi ,
i=1
przy podziale Pm oraz dowolnie wybranych punktów
ci ∈< xi−1 , xi >, i = 1, 2, . . . , nm .
Ciąg podziałów nazywamy normalnym ciągiem podziałów, jeżeli
lim δm = 0
m→∞
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Definicja
Własności
Przykłady
Definicja
Jeżeli ciąg {Sm } dla m → ∞ jest zbieżny i do tej samej granicy przy
każdym normalnym ciągu podziałów, niezależnie od wyboru punktów ci ,
to funkcję f (x) nazywamy funkcją całkowalną w przedziale < a, b >.
Granicę ciągu {Sm } nazywamy całką oznaczoną funkcji f (x) w granicach
od a do b i oznaczamy symbolem
Z
b
f (x) dx
a
Jeżeli przy jakimś ciągu normalnym podziałów ciąg {Sm } ma granicę
niezależną od wyboru punktów ci , to funkcja f (x) jest całkowalna.
Funkcja ciągła w przedziale domkniętym jest całkowalna
Funkcja ogranicznona w przedziale domkniętym oraz ciągła w nim z
wyjątkiem co najwyżej skończonej liczby liczby punktów jest
całkowalna.
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
1
Jeżeli a ≤ b ≤ b ≤ c, to
Zc
Zb
f (x) dx =
a
2
Definicja
Własności
Przykłady
Zc
f (x) dx +
c
b
Stały czynnik można wyłączyć przed znak całki
Zb
Zb
kf (x) dx = k
a
3
f (x) dx
f (x) dx
a
Całka sumy równa się sumie całek
Zb
Zb
(f (x) + g (x)) dx =
a
f (x) dx +
a
Stanisław Jaworski
Zb
g (x) dx
a
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
1
Jeżeli a ≤ b ≤ b ≤ c, to
Zc
Zb
f (x) dx =
a
2
Definicja
Własności
Przykłady
Zc
f (x) dx +
c
b
Stały czynnik można wyłączyć przed znak całki
Zb
Zb
kf (x) dx = k
a
3
f (x) dx
f (x) dx
a
Całka sumy równa się sumie całek
Zb
Zb
(f (x) + g (x)) dx =
a
f (x) dx +
a
Stanisław Jaworski
Zb
g (x) dx
a
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
1
Jeżeli a ≤ b ≤ b ≤ c, to
Zc
Zb
f (x) dx =
a
2
Definicja
Własności
Przykłady
Zc
f (x) dx +
c
b
Stały czynnik można wyłączyć przed znak całki
Zb
Zb
kf (x) dx = k
a
3
f (x) dx
f (x) dx
a
Całka sumy równa się sumie całek
Zb
Zb
(f (x) + g (x)) dx =
a
f (x) dx +
a
Stanisław Jaworski
Zb
g (x) dx
a
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
1
Definicja
Własności
Przykłady
Jeżeli funkcja f (x) jest ciągła w przedziale < a, b >, to zachodzi
Zb
f (x) dx = f (c)(b − a),
a
2
dla pewnego c z przedziału < a, b >
Jeżeli funkcja f (t) jest ciągła w przedziale < a, b >, to funkcja
Z x
h(x) =
f (t) dt
a
3
jest ciągła i różniczkowalna względem zmiennej x w przedziale
< a, b > i w każdym punkcie tego przedziału zachodzi związek
h0 (x) = f (x).
ZWIĄZEK MIĘDZY CAŁKĄ OZNACZONĄ A NIEOZNACZONĄ.
Jeżeli prz F (x) oznaczymy funkcję pierwotną funkcji f (x), ciągłej w
przedziale < a, b >, tzn. jeżeli F (x)0 = f (x), to ma miejsce wzór
Z b
f (x) dx = F (b) − F (a)
a
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
1
Definicja
Własności
Przykłady
Jeżeli funkcja f (x) jest ciągła w przedziale < a, b >, to zachodzi
Zb
f (x) dx = f (c)(b − a),
a
2
dla pewnego c z przedziału < a, b >
Jeżeli funkcja f (t) jest ciągła w przedziale < a, b >, to funkcja
Z x
h(x) =
f (t) dt
a
3
jest ciągła i różniczkowalna względem zmiennej x w przedziale
< a, b > i w każdym punkcie tego przedziału zachodzi związek
h0 (x) = f (x).
ZWIĄZEK MIĘDZY CAŁKĄ OZNACZONĄ A NIEOZNACZONĄ.
Jeżeli prz F (x) oznaczymy funkcję pierwotną funkcji f (x), ciągłej w
przedziale < a, b >, tzn. jeżeli F (x)0 = f (x), to ma miejsce wzór
Z b
f (x) dx = F (b) − F (a)
a
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
1
Definicja
Własności
Przykłady
Jeżeli funkcja f (x) jest ciągła w przedziale < a, b >, to zachodzi
Zb
f (x) dx = f (c)(b − a),
a
2
dla pewnego c z przedziału < a, b >
Jeżeli funkcja f (t) jest ciągła w przedziale < a, b >, to funkcja
Z x
h(x) =
f (t) dt
a
3
jest ciągła i różniczkowalna względem zmiennej x w przedziale
< a, b > i w każdym punkcie tego przedziału zachodzi związek
h0 (x) = f (x).
ZWIĄZEK MIĘDZY CAŁKĄ OZNACZONĄ A NIEOZNACZONĄ.
Jeżeli prz F (x) oznaczymy funkcję pierwotną funkcji f (x), ciągłej w
przedziale < a, b >, tzn. jeżeli F (x)0 = f (x), to ma miejsce wzór
Z b
f (x) dx = F (b) − F (a)
a
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
1
Definicja
Własności
Przykłady
Jeżeli u i v są funkcjami zmiennej x mającymi ciągłą pochodną, to
Z
b
u dv =
[uv ]ba
b
Z
−
vdu.
a
a
Jest to wzór na całkowanie przez części dla całek oznczonych.
2
Jeżeli g 0 (x) jest funkcją ciągłą, g (x) funkcją rosnącą w przedziale
< a, b >, a f (u) funkcją ciągłą w przedziale < g (a), g (b) >, to
zachodzi następujący wzór:
Z
b
f (g (x))g 0 (x) dx =
a
Z
g (b)
f (u) du
g (a)
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
1
Definicja
Własności
Przykłady
Jeżeli u i v są funkcjami zmiennej x mającymi ciągłą pochodną, to
Z
b
u dv =
[uv ]ba
b
Z
−
vdu.
a
a
Jest to wzór na całkowanie przez części dla całek oznczonych.
2
Jeżeli g 0 (x) jest funkcją ciągłą, g (x) funkcją rosnącą w przedziale
< a, b >, a f (u) funkcją ciągłą w przedziale < g (a), g (b) >, to
zachodzi następujący wzór:
Z
b
f (g (x))g 0 (x) dx =
a
Z
g (b)
f (u) du
g (a)
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Definicja
Własności
Przykłady
Przykłady
1
2π
R
0
x sin x dx = −
R
1
2π
0
1
2π
1
[sin x]0 = 1
R
Ponieważ x sin(x 2 ) dx =
Z
π/2
x sin(x 2 ) dx =
0
Ponieważ
Z
R
π
xd(cos x) = [−x cos x]02 +
− cos(x 2 )
2
− cos(x 2 )
2
1
2π
0
cosx dx =
+ C , mamy
π/2
=
0
R
− cos((π/2)2 )
− cos(02 )
−
2
2
e x x dx = e x (−1 + x) + C , mamy
3
e x x dx = [e x (−1 + x)]32 = e 3 (−1 + 3) − e 2 (−1 + 2)
2
R5
R5
R5
5
ln(x) dx = 2 x 0 ln(x) dx = [xln(x)]2 − 2 x ·
= 5 ln(5) − 2 ln(2) − (5 − 2)
2
Stanisław Jaworski
1
x
dx =
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Definicja
Własności
Przykłady
Przykłady
1
2π
R
0
x sin x dx = −
R
1
2π
0
1
2π
1
[sin x]0 = 1
R
Ponieważ x sin(x 2 ) dx =
Z
π/2
x sin(x 2 ) dx =
0
Ponieważ
Z
R
π
xd(cos x) = [−x cos x]02 +
− cos(x 2 )
2
− cos(x 2 )
2
1
2π
0
cosx dx =
+ C , mamy
π/2
=
0
R
− cos((π/2)2 )
− cos(02 )
−
2
2
e x x dx = e x (−1 + x) + C , mamy
3
e x x dx = [e x (−1 + x)]32 = e 3 (−1 + 3) − e 2 (−1 + 2)
2
R5
R5
R5
5
ln(x) dx = 2 x 0 ln(x) dx = [xln(x)]2 − 2 x ·
= 5 ln(5) − 2 ln(2) − (5 − 2)
2
Stanisław Jaworski
1
x
dx =
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Definicja
Własności
Przykłady
Przykłady
1
2π
R
0
x sin x dx = −
R
1
2π
0
1
2π
1
[sin x]0 = 1
R
Ponieważ x sin(x 2 ) dx =
Z
π/2
x sin(x 2 ) dx =
0
Ponieważ
Z
R
π
xd(cos x) = [−x cos x]02 +
− cos(x 2 )
2
− cos(x 2 )
2
1
2π
0
cosx dx =
+ C , mamy
π/2
=
0
R
− cos((π/2)2 )
− cos(02 )
−
2
2
e x x dx = e x (−1 + x) + C , mamy
3
e x x dx = [e x (−1 + x)]32 = e 3 (−1 + 3) − e 2 (−1 + 2)
2
R5
R5
R5
5
ln(x) dx = 2 x 0 ln(x) dx = [xln(x)]2 − 2 x ·
= 5 ln(5) − 2 ln(2) − (5 − 2)
2
Stanisław Jaworski
1
x
dx =
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Definicja
Własności
Przykłady
Przykłady
1
2π
R
0
x sin x dx = −
R
1
2π
0
1
2π
1
[sin x]0 = 1
R
Ponieważ x sin(x 2 ) dx =
Z
π/2
x sin(x 2 ) dx =
0
Ponieważ
Z
R
π
xd(cos x) = [−x cos x]02 +
− cos(x 2 )
2
− cos(x 2 )
2
1
2π
0
cosx dx =
+ C , mamy
π/2
=
0
R
− cos((π/2)2 )
− cos(02 )
−
2
2
e x x dx = e x (−1 + x) + C , mamy
3
e x x dx = [e x (−1 + x)]32 = e 3 (−1 + 3) − e 2 (−1 + 2)
2
R5
R5
R5
5
ln(x) dx = 2 x 0 ln(x) dx = [xln(x)]2 − 2 x ·
= 5 ln(5) − 2 ln(2) − (5 − 2)
2
Stanisław Jaworski
1
x
dx =
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Całki funkcji nieograniczonych
Całki oznaczone w przedziale nieskończonym
Definicja
Jeżeli funkcja f (x) jest ograniczona i całkowalna w każdym przedziale
a ≤ x ≤ c − h, h > 0, oraz w każdym przedziale c + k ≤ x ≤ b, k > 0, i
jeżeli istnieją granice
Z
lim+
h→0
c−h
Z
f (x) dx
oraz
a
lim+
k→0
b
f (x) dx,
c+k
to sumę tych granic nazywamy całką niewłaściwą funkcji f (x) w
przedziale < a, b > i oznaczamy symbolem
Z
b
f (x) dx
a
W podanej definicji chodzi o funkcje, które w każdym otoczeniu
(c − δ, c + δ), δ > 0, są niogranczone. W punkcie c funkcja może
nawet nie być okreśłona. Jeżeli przynajmniej jedna z granic nie
istnieje, to mówimy, że całka jest rozbieżna.
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Całki funkcji nieograniczonych
Całki oznaczone w przedziale nieskończonym
Jeżeli punktem nieograniczoności jest jeden z końców przedziału
< a, b >, to przez całkę niewłaściwą rozumiemy odpowiednio
Z
lim+
h→0
b
Z
f (x) dx
a+h
Przykład:
R3
R 3 dx
√ dx = lim
0
x
+ ε
ε→0
albo
dx
√
x
lim+
k→0
b−k
f (x) dx,
a
√
√ dx = lim+ 2 3 − 2 ε
ε→0
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Całki funkcji nieograniczonych
Całki oznaczone w przedziale nieskończonym
Definicja
Jeżeli funkcja f (x) jest ograniczona i całkowalna w każdym przedziale
skończonym a ≤ x ≤ v (a − ustalone, v − dowolne) oraz istnieje granica
Z v
lim
f (x) dx,
v →∞
a
to granicę tę nazywamy całką niewłaściwą funkcji f (x) w przedziale
a ≤ x < ∞ i oznaczamy symbolem
Z ∞
f (x) dx.
a
Analogicznie określa się znaczenie symbolu
Rb
lim u f (x) dx.
Rb
−∞
f (x) dx jako granicę
u→−∞
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Całki funkcji nieograniczonych
Całki oznaczone w przedziale nieskończonym
Przykład.
Chcemy obliczyć całkę
Ponieważ
mamy
R∞
1
2
x
R
2
x
+
+
1 2
x2
1 2
x2
R∞
1
2
x
+
1 2
x2
dx = − x4 −
2
x2
dx.
−
1
3x 3 ,
dx = limv →∞ − v4 −
Stanisław Jaworski
2
v2
−
1
3v 3
− (−4 − 2 − 1/3)
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Twierdzenie Taylora
Założenie: f ∈ C n+1 (< a, b >), a < x < b.
Teza:
f (x) = f (a) +
x − a (1)
(x − a)2 (2)
f (a) +
f (a) + . . . +
1!
2!
Z x
(x − a)n (n)
(x − t)n (n+1)
+
f (a) +
f
(t) dt
n!
n!
a
Ostatni wyraz często nazywa się n−tą resztą i oznacza przez
Rn (x, a).
n+1
W
(n+1)
Lagrange pokazał, że
Rn (x, a) = (x−a)
(a + θ(x − a))
(n+1)! f
0≤θ≤1
Szereg potęgowy f (x) = f (a) +
∞
P
n=1
f (n) (a)
n! (x
− a)n nazywamy
szeregiem Taylora.
Dla a = 0 szerec Taylora nazywa się szeregiem Maclaurina.
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Twierdzenie
Funkcja jest rozwijalna w szereg Taylora w przedziale (a − δ, a + δ),
δ > 0, jeżeli w tym przedziale:
1. funkcja ma pochodne każdego rzędu
2. lim Rn (x, a) = 0 dla x z przedziału (a − δ, a + δ)
n→∞
Warunek 2. jest w szczególności spełniony, jeżeli istnieje M > 0 takie, że
^
|f (n) (x)| < M
x∈(a−δ,a+δ)
Przykłady.
2
3
n
e x = 1 + x + x2! + x3! + . . . + xn! + . . .
3
4
3
x 4k+1
sin x = x − x3! + x4! + 55! − . . . + (4k+1)!
−
Stanisław Jaworski
x 4k+3
(4k+3)!
+ ...
Pochodne i całki, macierze i wyznaczniki
Podstawowe definicje
Działania na macierzach - podstawy
Wyznacznik macierzy
Układ równań liniowych
Formy kwadratowe i ich określoność
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
MACIERZE
Macierz wymiaru m × n
Macierz A wymiaru m × n jest prostokątną tablicą elementów
aij , i = 1, . . . m, j = 1, . . . , n:


a11 a12 . . . a1n
 a21 a22 . . . a2n 


A= .
..
.. 
..
 ..
.
.
. 
am1
am2
...
amn
Elementami macierzy mogą być liczby rzeczywiste, zespolone i „inne
jeszcze obiekty”. Będziemy oznaczać w skrócie A = (aij )
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Podstawowe definicje
Działania na macierzach - podstawy
Wyznacznik macierzy
Układ równań liniowych
Formy kwadratowe i ich określoność
Macierz zerowa to macierz, której wszystkie elementy są równe zero
Transpozycją macierzy A = (aij ) o wymiarach m × n jest macierz
AT = (aji ) o wymiarach n × m
O macierzy A wymiaru m × n powiemy, że jest kawdratowa, jeżeli m = n
Macierz A jest symetryczna, gdy jest kwadratowa oraz zachodzi
warunek AT = A
Macierz A = (aij ) jest diagonalna, jeżeli jest kwadratowa oraz aij = 0
dla i 6= j
Macierz identycznościowa I : macierz diagonalna, która ma same
jedynki na przekątnej
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Podstawowe definicje
Działania na macierzach - podstawy
Wyznacznik macierzy
Układ równań liniowych
Formy kwadratowe i ich określoność
Sumą macierzy A = (aij ) oraz B = (bij ) o jednakowych wymiarach jest
macierz A + B = (aij + bij )
Różnicą macierzy A = (aij ) oraz B = (bij ) o jednakowych wymiarach
jest macierz A − B = (aij − bij )
Mnożenie macierzy A = (aij ) przez liczbę α:
αA = (α · aij )
Przemienność, łączność oraz rozdzielność mnożenia macierzy przez
liczbę (α, β ∈ R):
αA = Aα, α(βA) = (αβ)A, (α ± β)A = αA ± βB, α(A ± B) = αA ± αB
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Podstawowe definicje
Działania na macierzach - podstawy
Wyznacznik macierzy
Układ równań liniowych
Formy kwadratowe i ich określoność
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Mnożenie macierzy A = (aij ) wymiaru m × n przez wektor
v = [v1 , . . . , vn ]T :


 
a11 a12 . . . a1n
v1
a11 v1 + a12 v2 + . . . + a1n vn
 a21 a22 . . . a2n   v2   a21 v1 + a22 v2 + . . . + a2n vn


 
A= .
  ..  = 
..
..
..
 ..
 .  
.
.
.
am1
am2
...
amn
Stanisław Jaworski
vn
am1 v1 + am2 v2 + . . . + amn vn
Pochodne i całki, macierze i wyznaczniki





Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Podstawowe definicje
Działania na macierzach - podstawy
Wyznacznik macierzy
Układ równań liniowych
Formy kwadratowe i ich określoność
Mnożenie macierzy A = (aij ) wymiaru m × n przez macierz
B = (b1 , b2 , . . . , bk ) wymiaru n × k:
AB = (Ab1 , Ab2 , . . . , Abk )
Transpozycja a mnożenie macierzy: (AB)T = B T AT
Rząd macierzy
Dla każdej macierzy A maksymalna liczba r liniowo niezależnych kolumn
jest równa maksymalnej liczbie liniowo niezależnych wierszy. Liczbę r
nazywamy rzędem macierzy, symbolicznie oznczanym przez R(A)
Macierz nieosobliwa: Macierz kwadratowa A wymiaru n × n, dla której
R(A)=n.
Macierz odwrotna A−1 do macierzy kwadratowej A:
A−1 A = I = AA−1
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Podstawowe definicje
Działania na macierzach - podstawy
Wyznacznik macierzy
Układ równań liniowych
Formy kwadratowe i ich określoność
Wyznacznik macierzy A wymiaru n × n (kwadratowej)
Wyznacznik to funkcja (oznaczona przez det)
det : { zbiór macierzy kwadratowych} → R
o własnościach:
det(I ) = 1
det(A) = 0 jeżeli A ma dwa sąsiednie wiersze równe
det jest funkcją liniową względem dowolnego wiersza
Uwaga: istnieje tylko jedna taka funkcja
Uwaga: Na nstępnych slajdach A(ij) oznacza macierz powstałą z
macierzy A poprzez usunięcie z niej i-tego wiersza oraz j−tej kolumny.
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Podstawowe definicje
Działania na macierzach - podstawy
Wyznacznik macierzy
Układ równań liniowych
Formy kwadratowe i ich określoność
Własności wyznaczników:
Twierdzenie Laplace’a dla kolumn:
det(A) =
n
X
aij (−1)i+j det(A(i, j))
i=1
dla i = 1, . . . , n
det(A) = 0 ⇔ R(A) < n
det(A) = −det(B), jeżeli B powstaje z A przez zamianę miejscami
dwóch wierszy macierzy A
det(A) = det(B), jeżeli B powstaje z A przez dodanie/odjęcie od
danego wiersza innego wiersza przemnożonego przez dowolną liczbę
Twierdzenie Cauchy’ego: det(AB) = det(A)det(B)
Jeżeli R(A) = n (macierz A jest pełnego rzędu), to
det(A−1 ) = (det(A))−1
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Podstawowe definicje
Działania na macierzach - podstawy
Wyznacznik macierzy
Układ równań liniowych
Formy kwadratowe i ich określoność
Własności wyznaczników:
Twierdzenie Laplace’a dla wierszy:
det(A) =
n
X
aij (−1)i+j det(A(i, j))
j=1
dla i = 1, . . . , n
det(A) = −det(B), jeżeli B powstaje z A przez zamianę miejscami
dwóch kolumn macierzy A
det(A) = det(B), jeżeli B powstaje z A przez dodanie/odjęcie od
danej kolumny innej kolumny przemnożonej przez dowolną liczbę
det(A) jest funkcją liniową dowolnej kolumny
det(AT ) = det(A)
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Podstawowe definicje
Działania na macierzach - podstawy
Wyznacznik macierzy
Układ równań liniowych
Formy kwadratowe i ich określoność
Niech A = (aij ) macierz wymiaru n × n, c = [c1 , . . . , cn ]T oraz
x = [x1 , . . . , xn ]T . Macierz A oraz wektor c traktujemy jako znane, a
wektor x jako nieznany (wektor niewiadomych). Interesuje nas
rozwiązanie układu równań Ax = c, tzn.


 a11 x1 + a12 x2 + . . . + a1n xn = c1

 a21 x1 + a22 x2 + . . . + a2n xn = c2
..

.



an1 x1 + an2 x2 + . . . + ann xn = cn
Twierdzenie. Jeżeli det(A) 6= 0, to powyższy układ równań liniowych
ma dokładnie jedno rozwiązanie. Rozwiązanie to można uzyskać za
pomocą wzorów Cramera:
xi =
det(a1 , a2 , . . . , ai−1 , c, ai+1 , . . . an )
,
det(A)
i = 1, 2, . . . , n,
gdzie ai oznacza i−tą kolumnę macierzy A
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Podstawowe definicje
Działania na macierzach - podstawy
Wyznacznik macierzy
Układ równań liniowych
Formy kwadratowe i ich określoność
Niech A = (aij ) macierz wymiaru m × n, c = [c1 , . . . , cm ]T oraz
x = [x1 , . . . , xn ]T . Interesuje nas rozwiązanie układu równań Ax = c, tzn.

a11 x1 + a12 x2 + . . . + a1n xn = c1



 a21 x1 + a22 x2 + . . . + a2n xn = c2
..

.



am1 x1 + am2 x2 + . . . + amn xn = cm
Niech



A=

a11
a21
..
.
a12
a22
..
.
...
...
..
.
a1n
a2n
..
.
am1
am2
...
amn








B=

a11
a21
..
.
a12
a22
..
.
...
...
..
.
a1n
a2n
..
.
c1
c2
..
.
am1
am2
...
amn
cm





Twierdzenie Kroneckera-Capellego. Powyższy układ równań liniowych
ma rozwiązanie wtedy i tylko wtedy, gdy R(A) = R(B) = r , przy tym
1) jeżeli r = n, to układ ma jedno rozwiązanie,
2) jeżeli r < n, to układ ma nieskończenie wiele rozwiązań i są one
zależne od n − r parametrów.
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Podstawowe definicje
Działania na macierzach - podstawy
Wyznacznik macierzy
Układ równań liniowych
Formy kwadratowe i ich określoność
Niech A = (a1 , . . . , an ) będzie macierzą wymiaru n × n. Wektory
a1 , . . . , an są jej kolumnami. Oznaczmy przez dAij wyznacznik z macierzy
(a1 , . . . , ai−1 , ei , ai+1 , . . . , an ), która powstała z A poprzez zamianę
kolumny aj na wektor ei = [0, . . . , 0, 1, 0, . . . , 0]T (który na i−tym
miejscu ma jedynkę, a poza tym same zera).
Macierz stowarzyszona AdjA do macierzy A:

dA11 dA12 . . . dA1n
 dA21 dA22 . . . dA2n

AdjA =  .
..
..
..
 ..
.
.
.
dAn1 dAn2 . . . dAnn





Twierdzenie: Macierz odwrotną do macierzy A można wyznaczyć
według wzoru:
1
)
A−1 = AdjA · (
det(A)
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Podstawowe definicje
Działania na macierzach - podstawy
Wyznacznik macierzy
Układ równań liniowych
Formy kwadratowe i ich określoność
Forma kwadratowa
Niech x = [x1 , . . . , xn ]T będzie wektorem n wymiarowym oraz niech
A = (aij ) będzie macierzą symetryczną
Pn Pn stopnia n (wymiaru n × n).
Odwzorowanie x → x T Ax = i=1 j=1 aij xi xj nazywamy formą
kwadratową
Macierz symetryczna A jest
dodatnio określona: x T Ax > 0 dla każdego x 6= 0 (piszemy A > 0)
ujemnie określona: x T Ax < 0 dla każdego x 6= 0 (piszemy A < 0)
niedodatnio określona: x T Ax ≤ 0 dla każdego x 6= 0 (piszemy A ≤ 0)
nieujemnie określona: x T Ax ≥ 0 dla każdego x 6= 0 (piszemy A ≥ 0)
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki
Całka oznaczona
Całka niewłaściwa
Wzór Taylora
Macierze
Podstawowe definicje
Działania na macierzach - podstawy
Wyznacznik macierzy
Układ równań liniowych
Formy kwadratowe i ich określoność
Kryterium Sylvestera
Macierz symetryczna A = (aij ) stopnia n jest dodatnio określona wtedy i
tylko wtedy, gdy wszystkie jej wiodące minory główne są dodatnie:
a11 > 0



det 

a11
a21
..
.
a12
a22
..
.
...
...
..
.
ak1
ak2
...

a1k
a2k 

 > 0, dla k = 2, . . . , n

akk
Uwaga: Jeżeli chcemy sprawdzić, czy macierz jest ujemnie określona,
należy sprawdzić, czy macierz „−A”jest określona dodatnio
Stanisław Jaworski
Pochodne i całki, macierze i wyznaczniki