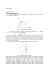Moc i wolne, a punkt

Tłumienność torów radiowych
Propagacja w wolnej przestrzeni
Plik nr 3
Tłumienność rośnie wraz ze wzrostem częstotliwości
Założenia przy obliczaniu
tłumienności
• Kierunki maksymalnego promieniowania i
maksymalnej czułości pokrywają się
• Istnieje dopasowanie falowe (brak odbić)
• Polaryzacja anten jest zgodna
• Przestrzeń międzyantenowa jest
jednorodna i oddalona od ziemi (np..
Suche powietrze); brak jest w niej
jakichkolwiek obiektów
Jeżeli antena nadawcza jest izotropowa i promieniuje moc
P (fala kulista), to powierzchniowa gęstość mocy
w odległości r wynosi:
P
S=
2
4πr
A uśredniony wektor Poyntinga dla fali lokalnie płaskiej
w punkcie odbioru:
S=
r2
E
2Z 0
=
r2
E
240π
Po porównaniu obu wzorów:
60 P
Emaks =
r
30 P
Esk =
r
Amplituda
Wartość
skuteczna
Jeżeli antena ma zysk energetyczny GT a do jej
zacisków doprowadzono moc PT, to:
Emaks
60 PT GT
=
r
Fale rozchodzące się w ośrodkach rzeczywistych
ulegają tłumieniu – współczynnik osłabienia A:
GT GR λ
2
PR = PT
A
2
(4πr )
2
W postaci logarytmicznej:
PR=PT + 20 log (λ/4πr) + GT + GR + A
[dB]
Tłumienność wolnej przestrzeni
 4πr 
A = 20 lg

 λ 
Np. dla odległości (r) 1 km
Dla λ=1m (f=300 MHz) A wynosi około 80 dB
Dla λ=10m (30 MHz) – A=60 dB
Przy podwojeniu odległości ∆A = 20 lg 2 = 6 dB
Porównanie tłumienności kabli i
wolnej przestrzeni
• Typowa tłumienność kabla A=10dB/km
przy 30 MHz
odległość
kabel
przestrzeń
1 km
10 dB
60 dB
2 km
20 dB
66 dB
4 km
40 dB
72 dB
8 km
80 dB
78 dB
16 km
160 dB 84 dB
Zasada Huygensa
• Każdy punkt ośrodka, do którego dotarło czoło
fali, można traktować jako źródło nowej fali
kulistej.
• Fale te (cząstkowe) interferują ze sobą i
wypadkową falą jest powierzchnia styczna do
wszystkich powierzchni fal cząstkowych
• Zjawisko wynikające bezpośrednio z zasady
Huygensa – DYFRAKCJA (uginanie się fali na
przeszkodach)
Amplituda fali po ugięciu
• Jeżeli na drodze fali znajdzie się przeszkoda
z pojedynczym otworem, amplituda fali
będzie największa w tym kierunku, w jakim
się przed przeszkodą rozchodziła.
• W zależności od kąta α (między kierunkiem
rozchodzenia się fali i przeszkodą),
amplituda wynosi: A(α)=1/2A0(1+cosα)
Strefy Fresnela
W punkcie O znajduje się antena nadawcza, w punkcie A –
odbiorcza. S0 jest przeszkodą. Dzielimy ją na współśrodkowe
okręgi, tak, aby fazy pól pochodzących od elementów
powierzchni leżących w granicach jednego pierścienia nie
różniły się więcej niż o 1800
Strefy Fresnela
• Pierścienie te – nazywane są strefami
Fresnela a ich promienie spełniają równanie:
nλ
ρ n + rn − ρ 0 − r0 =
2
W sąsiednich strefach składowe pola mają
przeciwne fazy; zakładając, że im krótsza fala,
tym mniejsza jest różnica w bezwzględnej
wartości E w poszczególnych strefach, przyjmuje
się założenie: każda składowa jest w przybliżeniu
równa średniej arytmetycznej składowych
pierścieni sąsiednich
E(A)= E1-E2+E3-E4+ …
E(A)=E1/2 + (E1/2 – E2 + E3/2) + (E3/2 –E4 + E5/2)+…
Dla n →∞ wyrażenia w nawiasach dążą do 0
Z wystarczającym przybliżeniem przyjmuje się, że:
Pole w punkcie obserwacji jest w przybliżeniu równe
sumie pól źródeł elementarnych rozmieszczonych na
połowie pierwszej strefy Fresnela
E(A) ≅ E1/2
Przybliżenie jest tym dokładniejsze, im silniejsza
jest nierówność:
ρ0 + r0 >> λ
Na propagację fal mają wpływ przeszkody
znajdujące się w obszarze pierwszej strefy
Fresnela
Dla łączy o podwyższonej niezawodności działania
cały obszar 1 strefy powinien być wolny od
przeszkód. Dla łączy o niższych wymaganiach
wystarczy zapewnić wolny obszar w strefie o
promieniu 0,6R
Przestrzenne strefy Fresnela
• Elipsoidy obrotowe, których ogniska stanowią
punkty umieszczenia anten