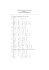Układy równań liniowych - Polsko

ALGEBRA LINIOWA. ĆWICZENIA
Układy Równań Liniowych
ALEXANDER DENISJUK
Najnowsza wersja tego dokumentu dostępna jest pod adresem
http://users.pjwstk.edu.pl/~denisjuk/
Ćwiczenie 1. Rozwiąż układ równań metodą eliminacji Gaussa i znajdź jedno rozwiązanie szczególne:
(1)
(2)
(3)
(4)


5x1 + 3x2 + 5x3 + 12x4 = 10,
2x1 + 2x2 + 3x3 + 5x4 = 4,


x + 7x2 + 9x3 + 4x4 = 2;
 1

−9x1 + 10x2 + 3x3 + 7x4 = 7,
−4x1 + 7x2 + x3 + 3x4 = 5,


7x1 + 5x2 − 4x3 − 6x4 = 3;

2x1 + 5x2 − 8x3 = 8,



4x + 3x − 9x = 9,
1
2
3
2x1 + 3x2 − 5x3 = 7,



x + 8x2 − 7x3 = 12;
 1

−9x1 + 6x2 + 7x3 + 10x4 = 3,
−6x1 + 4x2 + 2x3 + 3x4 = 2,


−3x1 + 2x2 − 11x3 − 15x4 = 1;
(5)
(6)
(7)
(8)


12x1 + 9x2 + 3x3 + 10x4 = 13,
4x1 + 3x2 + x3 + 2x4 = 3,


8x + 6x2 + 2x3 + 5x4 = 7;
 1

−6x1 + 9x2 + 3x3 + 2x4 = 4,
−2x1 + 3x2 + 5x3 + 4x4 = 2,


−4x1 + 6x2 + 4x3 + 3x4 = 3;


8x1 + 6x2 + 5x3 + 2x4 = 21,





3x
 1 + 3x2 + 2x3 + x4 = 10,
4x1 + 2x2 + 3x3 + x4 = 8,



3x

1 + 3x2 + x3 + x4 = 15,


7x + 4x + 5x + 2x = 18;
1
2
3
4


6x1 + 4x2 + 5x3 + 2x4 + 3x5 = 1,

3x + 2x − 2x + x = 1,
1
2
3
4
9x1 + 6x2 + x3 + 3x4 + 2x5 = 2,



3x1 + 2x2 + 4x3 + x4 + 2x5 = 3.
Ćwiczenie 2. Zbadaj układ i znajdź rozwiązanie ogólne w zależności od parametru λ:
(1)
(2)
(3)
(4)
(5)

−6x1 + 8x2 − 5x3 − x4 = 9,




−2x1 + 4x2 + 7x3 + 3x4 = 1,

−3x
1 + 5x2 + 4x3 + 2x4 = 3,



−3x1 + 7x2 + 17x3 + 7x4 = λ;


λx1 + x2 + x3 = 1,
x1 + λx2 + x3 = 1,


x + x2 + λx3 = 1;
 1

(1 + λ)x1 + x2 + x3 = 1,
x1 + (1 + λ)x2 + x3 = λ,


x1 + x2 + (1 + λ)x3 = λ2 ;


8x1 + 6x2 + 3x3 + 2x4 = 5,

−12x − 3x − 3x + 3x = −6,
1
2
3
4
4x1 + 5x2 + 2x3 + 3x4 = 3,



λx1 + 4x2 + x3 + 4x4 = 2;

2x1 + 5x2 + x3 + 3x4 = 2,



4x + 6x + 3x + 5x = 4,
1
2
3
4

4x
+
14x
+
x
+
7x
1
2
3
4 = 4,



2x1 − 3x2 + 3x3 + λx4 = 7;
(6)
(7)
(8)
(9)
1

2x1 − 1x2 + 3x3 + 4x4 = 5,




4x1 − 2x2 + 5x3 + 6x4 = 7,

6x1 − 3x2 + 7x3 + 8x4 = 9,



λx1 − 4x2 + 9x3 + 10x4 = 11;


2x1 + 3x2 + x3 + 2x4 = 3,

4x + 6x + 3x + 4x = 5,
1
2
3
4
6x1 + 9x2 + 5x3 + 6x4 = 7,



8x1 + 12x2 + 7x3 + λx4 = 9;

λx1 + x2 + x3 + x4 = 1,



x + λx + x + x = 1,
1
2
3
4

x
+
x
+
λx
+
x
1
2
3
4 = 1,



x + x2 + x3 + λx4 = 1;
 1
(1 + λ)x1 + x2 + x3 = λ2 + 3λ,

x1 + (1 + λ)x2 + x3 = λ3 + 3λ2 ,


x1 + x2 + (1 + λ)x3 = λ4 + 3λ3 ;
2
ALEXANDER DENISJUK
Ćwiczenie
 3. Znajdź rozwiązanie ogólne i bazę rozwiązań układu:

x1 + x2 − 2x3 + 2x4 = 0,




2x + 5x + 6x − 4x = 0,
x1 + x2 = 0,
1
2
3
4
(1)
(4) x1 + x2 + x3


4x1 + 5x2 − 2x3 + 3x4 = 0,



x2 + x3 = 0;


8x1 + 8x2 + 24x3 − 19x4 = 9;

x1 + x2 = 0,



x1 − x3 = 0,

x + x + x


1
2
3

x2 − x4 = 0,
(5)




x
+
x
+
x
2
3
4

−x + x − x = 0,


1
3
5
(2)
x + x5 = 0;
 4

−x2 + x4 − x6 = 0,




x1 + x2 = 0,




−x3 + x5 = 0,






x1 + x2 + x3
−x + x6 = 0;
 4
(6) x2 + x3 + x4


x1 − x3 + x5 = 0,




x4 + x5 + x6






x
−
x
+
x
=
0,
2
4
6

x + x = 0;
5
6
(3) x1 − x2 + x5 − x6 = 0,



x2 − x3 + x6 = 0,



x − x + x = 0;
1
4
5
= 0,
= 0,
= 0,
= 0,
= 0,
= 0,
Ćwiczenie 4.
(1) Znajdź wielomian f (x) drugiego stopnia, taki że f (1) = 8, f (−1) = 2, f (2) = 14.
(2) Znajdź wielomian f (x) drugiego stopnia, taki że f (1) = −8, f (−1) = 2, f (2) = 14.
(3) Znajdź wielomian f (x) trzeciego stopnia, taki że f (−2) = 1, f (−1) = 3, f (1) = 13, f (2) = 33.
(4) Znajdź wielomian f (x) stopnia 5, taki że f (−3) = −77, f (−2) = −13, f (−1) = 1, f (1) = −1,
f (2) = −17.
E-mail address: [email protected]
Polsko-Japońska Wyższa Szkoła Technik Komputerowych, Zamiejscowy Ośrodek Dydaktyczny w Gdańsku, ul. Brzegi 55, 80-045 Gdańsk