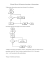Zastosowanie algorytmu EM do estymacji parametrów rozk∏adu na

Zeszyty
Naukowe nr
740
2007
Akademii Ekonomicznej w Krakowie
Roman Huptas
Katedra Statystyki
Zastosowanie algorytmu EM
do estymacji parametrów
rozk∏adu na podstawie danych
pogrupowanych
1. Wprowadzenie
W niniejszym artykule podjęty zostanie problem maksymalizacji wiarygodnościowej funkcji oceny, gdy w zbiorze danych występują zmienne, których wartości
z jakichś powodów nie zostały zaobserwowane. Algorytmem, który może posłużyć do rozwiązywania problemów brakujących danych w badanych strukturach
danych w kontekście wiarygodności, jest tzw. algorytm EM.
Algorytm EM jest skuteczną metodą iteracyjnego obliczania estymatorów największej wiarygodności (ENW)1, stosowaną w rozwiązywaniu wielu problemów
określanych jako problemy z niekompletnymi danymi, gdzie algorytmy takie jak
metoda Newtona-Raphsona mogą okazać się zbyt skomplikowane. W każdej iteracji algorytmu EM są wykonywane dwa kroki, nazywane krokiem E (expectation
step) i krokiem M (maximization step). Stąd jego nazwa – algorytm EM. Po raz
pierwszy nazwy tej użyli A.P. Dempster, N.M. Laird i D.B. Rubin w pracy [Dempster, Laird, Rubin 1977]. Na problemy z niekompletnymi danymi składają się nie
tylko sytuacje, gdy mamy do czynienia z ewidentnie niekompletnymi danymi,
takie jak: struktury z brakującymi danymi, modele z obciętymi rozkładami,
pogrupowane czy też ocenzurowane obserwacje, ale także problemy, gdzie niekompletność nie jest taka oczywista i naturalna. Do tych drugich zaliczymy model
efektów losowych, mieszanki rozkładów, estymację komponentów wariancyjnych,
1
Zob. [Magiera 2002, s. 146].
132
Roman Huptas
iteracyjną ważoną metodę najmniejszych kwadratów, analizę czynnikową czy też
modele logarytmiczno-liniowe.
Ze względu na zastosowanie algorytmu EM w rozwiązywaniu problemów
z brakującymi danymi jest on związany z pewną metodą estymacji ad hoc.
W metodzie tej parametry są estymowane po nadaniu brakującym danym pewnych wartości początkowych. Następnie te brakujące dane są „uwiarygadniane”
za pomocą wyestymowanych parametrów, a potem parametry są estymowane na
nowo, itd. aż do uzyskania zbieżności.
Główną ideą algorytmu EM jest powiązanie danego problemu z niekompletnymi danymi z odpowiednim problemem z danymi kompletnymi, dla którego
estymacja metodą największej wiarygodności jest pod względem obliczeniowym
dużo prostsza. Metodologia algorytmu EM opiera się na przeformułowaniu problemu z niekompletnymi danymi w terminach problemu z kompletnymi danymi,
który jest prostszy do rozwiązania, ustaleniu związku pomiędzy funkcjami wiarygodności tych dwóch problemów i wykorzystaniu prostszej pod względem obliczeniowym estymacji metodą największej wiarygodności do rozwiązania problemu
z danymi kompletnymi w kroku M algorytmu iteracyjnego.
Krok E algorytmu EM polega na „stworzeniu” danych dla problemu z danymi
kompletnymi przy użyciu zaobserwowanych danych niekompletnych, tak aby możliwe było wykonanie prostszego kroku M dla kompletnych danych. Mówiąc bardziej precyzyjnie, w kroku E tworzona jest funkcja wiarygodności dla problemu
z danymi kompletnymi. Opiera się ona częściowo na nieobserwowanych danych,
zatem jest ona zastępowana przez jej warunkową wartość oczekiwaną względem
obserwowanych danych. Krok E jest wykonywany przy użyciu bieżących wartości
dla nieznanych parametrów. W kroku M szukamy maksimum utworzonej w kroku
E funkcji wiarygodności. Rozpoczynając od odpowiedniej wartości początkowej
parametru, powtarzamy kroki E i M aż do uzyskania zbieżności.
Często w praktyce uzyskanie estymatorów największej wiarygodności może
nastręczać poważne trudności. Trudności te mogą wynikać np. z wielomodalności funkcji wiarygodności oraz niemożliwości uzyskania jawnych analitycznych
rozwiązań równań wiarygodności. W takich przypadkach można zastosować
iteracyjne metody znajdowania estymatorów największej wiarygodności. Pomocna
może okazać się tutaj metoda Newtona-Raphsona albo jej warianty.
Stosowanie metody Newtona-Raphsona może się wiązać z poważnymi trudnościami obliczeniowymi. Przypuśćmy, że liczba nieznanych parametrów w modelu
wynosi d. Metoda Newtona-Raphsona wymaga w każdej iteracji obliczenia macierzy informacji o wymiarach d × d oraz rozwiązania układu d równań liniowych.
Liczba wszystkich operacji arytmetycznych z tym związanych będzie bardzo duża
i będzie gwałtownie wzrastać, jeśli liczba d nieznanych parametrów będzie rosła.
Ponadto metoda Newtona-Raphsona, dla pewnych problemów, wymaga niereali-
Zastosowanie algorytmu EM do estymacji…
133
stycznie dokładnej wartości początkowej dla parametru, by ciąg rozwiązań iteracyjnych zbiegał do właściwego rozwiązania równań wiarygodności.
W rezultacie, gdy niefortunnie zostanie wybrany punkt startowy, algorytm
może „ugrzęznąć” w maksimum lokalnym. Dotyczy to zwłaszcza modeli statystycznych z wieloma parametrami. W przypadku innych metod typu Newtona
sytuacja wygląda podobnie. Alternatywą dla metod typu Newtona może być algorytm EM.
2. Opis algorytmu EM
Pojęcie danych niekompletnych zawiera w sobie typowe znaczenie brakujących
danych, tzn. takich, które są możliwe do uzyskania, ale również odnosi się do
sytuacji, w których dane kompletne byłyby możliwe do uzyskania tylko w ramach
hipotetycznego eksperymentu, którego realizacja nie jest praktycznie możliwa
(por. [McLachlan, Krishnan 1997, s. 21]).
Niech Y będzie wektorem losowym, modelującym obserwacje niekompletne,
o funkcji gęstości względem miary Lebesgueʼa g(y; Ψ), gdzie:
Ψ = (Ψ1, …, Ψd)T
jest wektorem nieznanych parametrów z przestrzeni parametrów Ω. Funkcja wiarygodności dla Ψ przy zadanym wektorze obserwacji y ma postać:
L (Ψ) = g(y; Ψ) .
~
Estymator największej wiarygodności jest definiowany jako rozwiązanie Ψ równania wiarygodności (por. [Magiera 2002, s. 167]):
∂
L(Ψ) = 0
∂Ψ
albo równoważnie:
∂
ln L (Ψ) = 0 ,
∂Ψ
(1)
w którym osiągane jest globalne maksimum L (Ψ).
Niech x będzie wektorem danych kompletnych. Wektor danych obserwowanych
y jest wówczas traktowany jako wektor danych niekompletnych i jako funkcja
danych kompletnych. Zatem y = y(x) (por. [Dempster, Laird, Rubin 1977, s. 1],
[McLachlan, Krishnan 1997, s. 22]).
Niech X będzie wektorem losowym, modelującym dane kompletne i mającym
funkcję gęstości względem miary Lebesgueʼa gc (x; Ψ). Wtedy logarytm funkcji
wiarygodności nieobserwowanych danych kompletnych ma postać:
Roman Huptas
134
ln Lc(Ψ) = ln gc (x; Ψ) .
Mamy, formalnie, dwie przestrzenie prób X i Y oraz odwzorowanie wielo-jednoznaczne z przestrzeni X w przestrzeń Y. Zamiast obserwować wektor danych
kompletnych x w przestrzeni X, obserwujemy wektor danych niekompletnych
y = y(x) w przestrzeni Y. Związek między funkcjami gęstości danych kompletnych
i danych niekompletnych ma postać:
g( y 0 ; Ψ) =
∫ χ( y ) gc (x; Ψ) dµ (x) ,
0
gdzie X(y0) = {x ∈ X : y(x) = y0}, μ(x) jest odpowiednio skonstruowaną miarą na
X(y0 ), a y0 jest ustalone.
Należy nadmienić, że w pracach [Dempster, Laird, Rubin 1977], [McLachlan,
Krishnan 1997] i [Wu 1983] kwestia odpowiednio skonstruowanej miary nie jest
poruszana. W pracach tych związek między gęstościami g i gc ma postać:
g( y 0 ; Ψ) =
∫ χ( y ) gc (x; Ψ) dx ,
0
co nie zawsze jest formalnie poprawne.
Algorytm EM rozwiązuje równanie wiarygodności (1) dla niekompletnych
danych pośrednio, wykorzystując logarytm funkcji wiarygodności kompletnych
danych ln L c (Ψ). Oczywiście, funkcja ln L c (Ψ) jest nieobserwowalna. Jest ona
zatem zastępowana przez jej warunkową wartość oczekiwaną względem wektora
Y, przy użyciu bieżącej wartości parametru Ψ.
Niech
Q (Ψ, Φ) = EΦ{ln Lc (Ψ) | Y = y} ,
gdzie operator E wartości oczekiwanej ma indeks dolny Φ w celu zaznaczenia,
że ta warunkowa wartość oczekiwana jest obliczana z użyciem wartości Φ dla
parametru Ψ.
Niech Ψ (0) będzie pewną wartością początkową parametru Ψ. Wtedy w pierwszej iteracji krok E wymaga obliczenia wyrażenia:
Q (Ψ, Ψ(0)) = EΨ (0){ln Lc (Ψ) | Y = y} .
W kroku M maksymalizujemy Q(Ψ, Ψ(0)) względem Ψ po całej przestrzeni parametrów Ω. Wybieramy zatem Ψ(1), takie że:
Q (Ψ(1), Ψ(0)) ≥ Q (Ψ, Ψ(0))
dla wszystkich Ψ ∈ Ω. W drugiej iteracji ponownie wykonywane są kroki E i M,
ale tym razem wartość parametru Ψ(0) jest zastąpiona przez Ψ(1) (wartość parametru Ψ uzyskana w pierwszej iteracji).
Zastosowanie algorytmu EM do estymacji…
135
Kroki E i M w (k + 1)-szej iteracji są zdefiniowane następująco (zob. [McLachlan, Krishnan 1997, s. 22])2:
Krok E. Obliczenie Q(Ψ, Ψ(k)), gdzie:
Q(Ψ, Ψ(k)) = EΨ (k){ln Lc (Ψ) | Y = y} ,
a Ψ(k) oznacza wartość parametru Ψ uzyskaną w k-tej iteracji algorytmu EM.
Krok M. Maksymalizacja Q(Ψ, Ψ (k)) względem Ψ. Wybieramy zatem
Ψ(k + 1) ∈ Ω, takie że:
Q(Ψ(k + 1), Ψ(k)) ≥ Q(Ψ, Ψ(k))
dla wszystkich Ψ ∈ Ω.
Dla zadanego ε > 0 kroki E i M są powtarzane do momentu, gdy po raz
pierwszy:
ln L(Ψ(k + 1)) – ln L(Ψ(k)) < ε ,
lub gdy zostanie spełnione inne kryterium zatrzymania, np. liczba iteracji osiągnie
zadaną z góry wartość maksymalną.
3. Estymacja parametrów rozkładu na podstawie danych
pogrupowanych i obci´tych
Do powstania problemu z niekompletnymi danymi, a następnie do zastosowania algorytmu EM, jako metody obliczania estymatorów największej wiarygodności, może prowadzić zagadnienie pogrupowanych i obciętych danych (zob.
[McLachlan, Krishnan 1997, s. 74], [Dempster, Laird, Rubin 1977, s. 13]). Poniżej
przedstawiony problem to sytuacja ewidentnie niekompletnych danych, choć
należy zaznaczyć, że określenie funkcji wiarygodności danych kompletnych nie
jest takie proste i oczywiste.
Niech W będzie zmienną losową z przestrzeni W o funkcji gęstości f(w; Ψ),
gdzie Ψ jest wektorem nieznanych parametrów. Niech przestrzeń W będzie
podzielona na v rozłącznych klas Wj (j = 1, …, v). Realizacje zmiennej losowej
W są niezależne, ale nie są rejestrowane. Jedynie liczby nj tych obserwacji, które
należą do klasy Wj dla j = 1, …, r, gdzie r ≤ v, są rejestrowane.
Niech wektor:
y = (n1, …, nr)T
będzie wektorem danych niekompletnych (zaobserwowanych) i oznaczmy:
2
Por. [Dempster, Laird, Rubin 1977, s. 6], [Wu 1983, s. 96].
Roman Huptas
136
r
n := ∑ n j .
(2)
j =1
W tym przypadku n traktujemy jako ustalone, co można zinterpretować w ten
sposób, że eksperyment, którego wynikiem jest W, jest przeprowadzony tyle razy,
aż liczba zaobserwowanych danych osiągnie n. Gdy nie obserwujemy nowych
danych, to nie wiemy, czy eksperyment nie został przeprowadzony, czy też jego
wynik trafił do jednej z nieobserwowanych klas. W efekcie liczba powtórzeń
eksperymentu jest nieznana i losowa. Równoważnie, można traktować wszystkie
występujące poniżej rozkłady jako warunkowe względem n.
Przy ustalonym n wektor y pochodzi z rozkładu wielomianowego o wielkości
próby n z r kategoriami, a prawdopodobieństwa wystąpienia kategorii wynoszą
pj (Ψ) / p(Ψ), j = 1, …, r, gdzie:
p j (Ψ ) =
∫W
f (w; Ψ ) dw ,
j
r
p(Ψ) = ∑ p j (Ψ) .
(3)
(4)
j =1
Funkcja wiarygodności dla niekompletnych danych ma postać:
L(Ψ ) =
r
1n j
 p (Ψ ) 
∏  pj(Ψ )  .
j =1
r
n!
∏nj !
(5)
j =1
Wprowadźmy wektor „brakujących” danych dla potrzeb algorytmu EM.
Niech
z = (nr + 1, …, nv)T
oraz
wj = (wj1, …, wjn )T,
j
j = 1, …, v,
gdzie z jest wektorem nieobserwowanych częstości w przypadku obciętych danych
(tzn. gdy r < v), a wj jest wektorem nj nieobserwowanych realizacji zmiennej losowej W, które należą do klasy Wj dla j = 1, …, v.
Niech teraz wektor danych kompletnych ma postać:
x = (yT, zT, w1T, …, wTv )T .
(6)
Zastosowanie algorytmu EM do estymacji…
137
Wektor losowy Y danych niekompletnych będzie miał rozkład wielomianowy,
a tym samym funkcję wiarygodności określoną wzorem (5), jeśli wektor losowy
X danych kompletnych będzie miał rozkład, dla którego funkcja wiarygodności
będzie miała postać (z dokładnością do mnożnika niezależnego od Ψ):
v
nj
Lc (Ψ) = ∏ ∏ f (w jk ; Ψ) ,
(7)
j =1 k =1
gdzie obserwacje wjk ( j = 1, …, v ; k = 1, …, nj ) są realizacjami zmiennej losowej W
dla próby o rozmiarze n + m, zaś:
m=
v
∑ nj
(8)
j = r +1
i jest losowe. Logarytm funkcji wiarygodności powinien więc mieć postać
(z dokładnością do składnika niezależnego od Ψ):
v
nj
ln Lc (Ψ) = ∑ ∑ ln f (w jk ; Ψ) .
(9)
j =1 k =1
Skonstruujmy rozkład brakujących danych tak, aby otrzymać (7) i (9). Funkcję
wiarygodności Lc (Ψ) przedstawmy jako iloczyn:
v
nj
Lc (Ψ) = L (Ψ) d (z | y; Ψ) ∏ ∏ h j (w jk ; Ψ) ,
(10)
j =1 k =1
gdzie d(z | y; Ψ) jest gęstością warunkową wektora losowego Z przy zadanym
Y = y, a hj (w; Ψ), j = 1, …, v, jest gęstością warunkową zmiennej losowej W przy
zadanych Y = y i Z = z, taką że:
h j (w; Ψ) =
f (w; Ψ)
,
p j (Ψ)
1, …,, v ,,
jj == 1,
(11)
tzn. obserwacje wjk (k = 1, …, nj) w celi Wj (j = 1, …, v) są próbą losową rozmiaru
nj z gęstości hj (w; Ψ). Pozostaje określić gęstość d(z | y; Ψ), tak aby Lc (Ψ) miała
postać równoważną (7).
Uwzględniając (5) i (11), logarytm funkcji wiarygodności postaci (10) wynosi:
v
nj
ln Lc ( Ψ ) = ln L ( Ψ ) + ln d (z | y; Ψ ) + ∑∑ ln h j (w jk ; Ψ ) =
j =1 k =1
r
= ∑ n j ln
j =1
p j (Ψ )
p( Ψ )
+ ln
r
n!
∏nj !
v
nj
+ ln d (z | y; Ψ ) + ∑∑ ln
j =1 k =1
f (w jk ; Ψ )
p j (Ψ )
=
j =1
v
nj
r
v
nj
= ∑∑ ln f (w jk ; Ψ ) +∑ n j ln p j ( Ψ ) − ∑∑ ln p j ( Ψ ) − n ln p( Ψ ) +
j =1 k =1
j =1
j =1 k =1
v
nj
ln Lc ( Ψ ) = ln L ( Ψ ) + ln d (z | y; Ψ ) + ∑∑ ln h j (w jk ; Ψ ) =Roman Huptas
138
j =1 k =1
r
= ∑ n j ln
j =1
p j (Ψ )
p( Ψ )
+ ln
r
n!
∏nj !
v
nj
+ ln d (z | y; Ψ ) + ∑∑ ln
j =1 k =1
f (w jk ; Ψ )
p j (Ψ )
=
j =1
nj
v
r
nj
v
= ∑∑ ln f (w jk ; Ψ ) +∑ n j ln p j ( Ψ ) − ∑∑ ln p j ( Ψ ) − n ln p( Ψ ) +
j =1 k =1
j =1
j =1 k =1
+ ln d (z | y; Ψ ) + ln
n!
r
∏nj !
.
j =1
Przekształcając dalej, otrzymujemy:
v
nj
ln Lc ( Ψ ) = ∑ ∑ ln f (w jk ; Ψ ) − ln( p( Ψ ))n −
j =1 k =1
v
∑ ln( p j (Ψ ))n + ln d (z | y; Ψ ) + ln
j
j = r +1
r
n!
∏nj !
=
j =1
v
v n


n
= ∑ ∑ ln f (w jk ; Ψ ) − ln ( p( Ψ ))n ∏ ( p j ( Ψ ))  + ln d (z | y; Ψ ) + ln


j =1 k =1
j = r +1
j
j
r
n!
∏nj !
.
(12)
j =1
Zatem (12) będzie, z dokładnością do składnika niezależnego od Ψ, równe (9),
jeśli d(z | y; Ψ) będzie określona następująco:
d (z | y; Ψ) = C ( p(Ψ))n
v
∏ ( p j (Ψ))n
j
.
(13)
j = r +1
Można pokazać (por. [McLachlan, Krishnan 1997, s. 77]), że (13) zadaje funkcję
gęstości, gdy C =
( m + n − 1)!
(n − 1)!
v
∏ nj !
.
j = r +1
Krok E dla (k+1)-szej iteracji
–
Obliczamy Q(Ψ, Ψ(k) ) = E Ψ(k) {lnL c (Ψ) | Y = y}. Niech Nj będzie zmienną
losową oznaczającą liczbę obserwacji w klasie Wj. Ze względu na konstrukcję
wektorów wj ( j = 1, …, v), z i y, otrzymujemy (por. [McLachlan, Krishnan 1997,
s. 77]):
Zastosowanie algorytmu EM do estymacji…
v
Q( Ψ , Ψ ( k ) ) = ∑ n(jk ) Q j ( Ψ , Ψ ( k ) ) + ln
j =1
139
( m + n − 1)! n
v
∏
j =1
gdzie:
i
n (jk ) !
,
(14)
Qj (Ψ, Ψ(k)) = EΨ(k){ln f (W; Ψ) | W ∈ Wj }

nj
dla
n(jk ) = EΨ ( k ) { N j | Y = y} = 
(k )
(k )
n p j ( Ψ ) p( Ψ ) dlaa
j = 1, …, r
j = r + 1, …, v .
człon (14) nie zależy od Ψ i może być opuszczony przy maksymalizacji
– Drugi
(k)
Q(Ψ, Ψ ). Zatem ostatecznie możemy przyjąć:
v
Q(Ψ, Ψ( k ) ) = ∑ n(jk ) Q j (Ψ, Ψ( k ) ) .
(15)
j =1
Krok M dla (k + 1)-szej iteracji
Maksymalizujemy Q(Ψ, Ψ(k) ) względem Ψ. Wartość parametru Ψ(k + 1) będzie
pierwiastkiem równania ∂Q(Ψ, Ψ(k) ) /∂ Ψ = 0, gdzie:
v
∂
∂
Q(Ψ, Ψ( k ) ) = ∑ n(jk )
Q j (Ψ, Ψ( k ) )
∂Ψ
∂Ψ
j =1
i
{
}
∂
∂
Q j (Ψ , Ψ ( k ) ) = E ( k )
ln f (W ; Ψ ) | W ∈ Wj .
Ψ
∂Ψ
∂Ψ
4. Eksperyment symulacyjny
Zastosowanie algorytmu EM do estymacji parametrów rozkładu dla danych
pogrupowanych, opisane szczegółowo w trzecim punkcie artykułu, skłoniło
do przeprowadzenia eksperymentu symulacyjnego z wykorzystaniem testu χ2
zgodności rozkładu próby losowej z rozkładem teoretycznym, w którym statystyka testowa, zwana statystyką χ2 Pearsona, ma asymptotyczny rozkład χ2 (zob.
[Magiera 2002, s. 244]). W naszym eksperymencie test był przeprowadzany
w przypadku, gdy rozkład teoretyczny postulowany w hipotezie zerowej był
ciągły i zależny od nieznanych parametrów. Gdy rozkład teoretyczny zależy od
nieznanych parametrów, wówczas częstości teoretyczne zależą oczywiście od tych
Roman Huptas
140
parametrów. Aby wyliczyć częstości, należy parametry oszacować. W praktyce
w celu wyestymowania parametrów dla testu stosuje się dwie metody:
1) jako oszacowania nieznanych parametrów przyjmuje się rozwiązania układu
równań wiarygodności, powstałego przy wykorzystaniu funkcji wiarygodności dla
obserwacji zgrupowanych (ENW są oparte na częstościach empirycznych);
2) jako estymatory parametrów przyjmuje się rozwiązania układu równań
wiarygodności dla niezgrupowanych danych (ENW są oparte na oryginalnych
obserwacjach, a obliczenia są zwykle dużo prostsze).
Niech pi będą częstościami teoretycznymi v klas w przypadku, gdy rozkład
teoretyczny jest w pełni określony. Wówczas statystyka χ2 Pearsona ma postać:
v
( N i − npi )2
,
npi
i =1
χ2 = ∑
gdzie Ni jest zmienną losową, której wartość ni dla próby prostej (x1, …, xn) równa
jest liczbie tych obserwacji spośród x1, …, xn, które należą do i-tej klasy przy
określonym podziale zbioru liczb rzeczywistych na v rozłącznych klas. Rozkładem
granicznym przy n → ∞ statystyki χ2 jest rozkład χ2 z v – 1 stopniami swobody.
Niech teraz p~ i będą ENW częstości teoretycznych pi, opartymi na częstościach
empirycznych ni (odpowiada to metodzie 1). Wtedy, przy odpowiednich warunkach regularności, statystyka:
v
~
( N − np )2
~
χ2 = ∑ i ~ i
npi
i =1
ma przy n → ∞ rozkład graniczny χ2 z v – 1 – k stopniami swobody, gdzie k jest
liczbą estymowanych parametrów.
Niech pˆ i będą ENW częstości teoretycznych pi, uzyskanymi dla niezgrupowanych danych, czyli opartymi na oryginalnych obserwacjach (odpowiada to metodzie 2). Wtedy statystyka testowa ma postać:
v
( N i − npˆ i )2
.
npˆ i
i =1
χˆ 2 = ∑
ˆ 2 leży między rozkłaOkazuje się, że rozkład graniczny przy n → ∞ statystyki χ
~2
2
2
ˆ ma więc pewien rozkład, któdami granicznymi statystyk χ i χ . Statystyka χ
rego kwantyle zawierają się między odpowiednimi kwantylami rozkładów χ 2v – k – 1
i χ 2v – 1 . W sposób bardziej precyzyjny mówi o tym następujące twierdzenie.
Twierdzenie 1 [Chernoff, Lehmann 1954]. Asymptotyczny rozkład statystyki
χˆ 2 jest taki jak rozkład:
Zastosowanie algorytmu EM do estymacji…
v − k −1
∑
i =1
yi2 +
141
v −1
∑ λi yi2 ,
i =v− k
gdzie yi są niezależne i pochodzą z rozkładu normalnego N(0, 1), a λi są z przedziału (0, 1) i mogą zależeć od estymowanych parametrów.
Należy nadmienić, że wraz ze wzrostem liczby v klas wartości kwantyli rozkładów χ 2v – k – 1 i χ 2v – 1 (przy tym samym poziomie istotności α) coraz mniej się
różnią. Jeżeli więc liczba klas jest duża i estymujemy małą liczbę parametrów
metodą największej wiarygodności bez grupowania obserwacji, to przy określaniu
obszaru krytycznego można korzystać z wartości kwantyli rozkładu χ2 z v – 1 – k
stopniami swobody. W przeciwnym wypadku używanie statystyki χˆ 2 z rozkładem
granicznym χ2 z v – 1 – k stopniami swobody (co jest dość powszechną praktyką)
powoduje, że rzeczywisty rozmiar testu może być istotnie większy niż zakładany
poziom istotności.
Celem eksperymentu symulacyjnego było porównanie, przy założonych poziomach istotności, empirycznych rozmiarów testów χ2 Pearsona uzyskanych w przypadkach, gdy nieznane parametry estymowane były na podstawie zgrupowanych
danych przy użyciu algorytmu EM oraz na podstawie danych oryginalnych, niezgrupowanych. Rozkład teoretyczny postulowany w hipotezie zerowej był ciągły.
Mieliśmy do czynienia z gęstością rozkładu normalnego z nieznanymi wartością
oczekiwaną μ i wariancją σ2, tzn.
f (w; Ψ) =
 ( w − µ )2 
1
exp −
,
2σ 2 
2 πσ

(16)
gdzie wektor Ψ nieznanych parametrów miał postać Ψ = (μ, σ 2)T.
Dla n-elementowych prób losowych z rozkładu N(0, 1) wyznaczane były liczności ni obserwacji, które znalazły się w kolejnych v podprzedziałach podziału
przedziału (–∞, ∞) postaci (–∞, a1], (a1, a2], …, (av – 2, av – 1], (av – 1, ∞). Estymatory były oparte na tych samych n-elementowych próbach. Po wyznaczeniu esty~2
ˆ2 i χ
. Obliczenia były powtarzane
matorów obliczane były statystyki testowe χ
N = 10 000 razy, za każdym razem dla różnego zestawu danych. Empiryczne
rozmiary testów αemp wyznaczane były dla obszaru krytycznego postaci:
K = {t: t > χ 2v− 3 (1 − α)} ,
gdzie χ 2v – 3(1 – α) jest kwantylem rzędu 1 – α rozkładu χ2 z v – 3 stopniami swobody, a α jest poziomem istotności. Do wygenerowania próby z rozkładu N(0, 1)
użyto generatorów ran1 oraz gamdev, zaczerpniętych z pracy [Press, Teukolsky,
Vetterling, Flannery 1995].
Roman Huptas
142
Wzory na estymatory parametrów μ i σ2 w przypadku algorytmu EM wyprowadzamy opierając się na opisie kroku M z punktu trzeciego uwzględniając, że
mamy do czynienia jedynie z danymi zgrupowanymi (tzn. r = v). Dla (16) funkcja
Q(Ψ, Ψ(k)) przyjmuje postać:
v
1
1
Q( Ψ , Ψ ( k ) ) = − n (ln 2 π + ln σ 2 ) − 2 ∑ n j EΨ ( k ) {(W − µ)2 | W ∈ Wj } ..
2
2σ j =1
Ostatecznie mamy Ψ(k + 1) = (μ(k + 1), (σ2)(k + 1))T, gdzie:
v
∑ n j E Ψ { W | W ∈ Wj }
(k )
µ
( k +1)
=
j =1
v
∑nj
j =1
i
v
∑ n j EΨ {(W − µ( k+1) )2 | W ∈ Wj }
(k )
2 ( k +1)
(σ )
=
j =1
v
∑nj
.
j =1
Warunkowe wartości oczekiwane zostały w programie obliczone w sposób numeryczny przy wykorzystaniu funkcji qromo, zaczerpniętej z pracy [Press, Teukolsky,
Vetterling, Flannery 1995], w celu obliczenia odpowiednich całek. Z kolei estymatory w przypadku danych oryginalnych obliczamy następująco:
~
µ=
n
1
∑ Xi
n i =1
~
σ2 =
n
1
2
( Xi − µ~ ) ,
∑
n i =1
a więc jako odpowiednie momenty z próby.
W tabelach wyników podane zostały założone poziomy istotności i empiryczne
rozmiary testów. Rozmiary empiryczne wyliczono jako:
α emp =
Nk
,
N
gdzie Nk to liczba tych wartości statystyk testowych, które wpadły do obszaru
krytycznego, a N oznacza liczbę powtórzeń symulacji. Za błąd symulacji przyjęto
górne oszacowanie Var ( N k N ) . Dla Nk ~ B(N, α0 ) mamy:
Zastosowanie algorytmu EM do estymacji…
N 
Var  k  =
N 
143
1
α 0 (1 − α 0 )
≤
Var ( N k ) =
2
N
N
1 3
⋅
4 4 ,
N
gdzie α0 jest rzeczywistym rozmiarem testu.
W tabelach 1–4 przedstawiono wyniki uzyskane dla N = 10 000 (błąd symulacji wynosi 0,004), liczności próby n ∈ {100; 500} i liczby klas v ∈ {4; 8}. Granice
klas zostały wyznaczone następująco:
– w przypadku v = 4 mamy (– ∞; –1], (–1; 0], (0; 1], (1; ∞),
– w pozostałych przypadkach mamy dwie skrajne klasy postaci (– ∞; –1,5]
i (1,5; ∞), a przedział (–1,5; 1,5] został podzielony na v – 2 równe podprzedziały.
Eksperyment pokazał, że przy estymacji nieznanych parametrów z wykorzystaniem funkcji wiarygodności po zgrupowaniu danych empiryczne rozmiary testów
są równe, w granicach błędu symulacji, założonym poziomom istotności niezależnie od liczby klas i liczności próbki. W przypadku estymacji parametrów na podstawie oryginalnych obserwacji empiryczne rozmiary testów odbiegają znacznie
od założonych poziomów istotności, gdy liczba klas jest mała. Zwiększając liczbę
klas obserwujemy, że empiryczne rozmiary testów coraz mniej się różnią między
sobą. Liczność próbki z kolei ma niewielki wpływ na rozmiary testów. Widzimy
więc, że sposób estymacji parametrów istotnie wpływa na wyniki testów.
Tabela 1. Empiryczne rozmiary testów dla v = 4, n = 100 i N = 10 000
Poziom istotności α
Empiryczny rozmiar testu αemp
algorytm EM
momenty z próby
0,010
0,010
0,015
0,050
0,052
0,085
0,100
0,104
0,172
Źródło: obliczenia własne.
Tabela 2. Empiryczne rozmiary testów dla v = 8, n = 100 i N = 10 000
Poziom istotności α
Empiryczny rozmiar testu αemp
algorytm EM
momenty z próby
0,010
0,009
0,011
0,050
0,050
0,055
0,100
0,103
0,113
Źródło: obliczenia własne.
Roman Huptas
144
Tabela 3. Empiryczne rozmiary testów dla v = 4, n = 500 i N = 10 000
Poziom istotności α
Empiryczny rozmiar testu αemp
algorytm EM
momenty z próby
0,010
0,010
0,015
0,050
0,054
0,084
0,100
0,104
0,173
Źródło: obliczenia własne.
Tabela 4. Empiryczne rozmiary testów dla v = 8, n = 500 i N = 10 000
Poziom istotności α
Empiryczny rozmiar testu αemp
algorytm EM
momenty z próby
0,010
0,011
0,011
0,050
0,053
0,059
0,100
0,105
0,118
Źródło: obliczenia własne.
5. Podsumowanie
W artykule został opisany algorytm EM oraz przykład jego zastosowania.
Algorytm EM jest postrzegany jako ogólna iteracyjna metoda optymalizacyjna
do maksymalizowania wiarygodnościowej funkcji oceny przy zadanym modelu
probabilistycznym z brakującymi danymi. Metoda ta jest wrażliwa na warunki
początkowe, stąd wybór różnych warunków początkowych może prowadzić do
uzyskania różnych maksimów lokalnych. W związku z powyższym, w praktyce,
w celu zmniejszenia prawdopodobieństwa zakończenia procesu optymalizacyjnego
na stosunkowo „nieefektywnym” maksimum lokalnym z punktu widzenia funkcji
wiarygodności, wskazane jest uruchomienie algorytmu EM z różnymi warunkami
początkowymi, a następnie wybranie rozwiązania, dla którego otrzymujemy największą wartość funkcji wiarygodności. Niemniej standardowy algorytm EM jest
powszechnie stosowany ze względu na dużą uniwersalność struktury i łatwość,
z jaką algorytm ten może być określony dla wielu różnych problemów.
Literatura
Chernoff H., Lehmann E.L. [1954], The Use of Maximum Likelihood Estimates in χ2
Tests for Goodness of Fit, „Annals of Mathematical Statistics”, vol. 25.
Zastosowanie algorytmu EM do estymacji…
145
Dempster A.P., Laird N.M, Rubin D.B. [1977], Maximum Likelihood from Incomplete Data
via the EM Algorithm (with Discussion), „Journal of the Royal Statistical Society B”,
vol. 39.
Magiera R. [2002], Modele i metody statystyki matematycznej, wyd. 1, GiS, Wrocław.
McLachlan G.J., Krishnan T. [1997], The EM Algorithm and Extensions, John Wiley and
Sons, New York.
Press W.H., Teukolsky S.A., Vetterling W.T., Flannery B.P. [1995], Numerical Recipes
in C. The Art of Scientific Computing, Cambridge University Press, New York.
Wu C.F.J. [1983], On the Convergence Properties of the EM Algorithm, „Annals of Statistics”, vol. 11.
The Application of the EM Algorithm to Estimation of Parameters
of Distribution in Case Data are Grouped
In this article, the Expectation-Maximization (EM) algorithm and its application are
presented. The EM algorithm is a powerful iterative technique for finding maximum
likelihood estimates, which is useful in a wide variety of situations best described as
“incomplete data problems”, where algorithms such as the Newton-Raphson method may
turn out to be more complicated. The popularity of the EM algorithm arises from its
simplicity in implementation, stability in convergence, and applicability in practice. In the
article, the E-step and M-step of the EM algorithm are illustrated with an application. The
application is related to estimating parameters of distribution in case data are grouped and
possibly truncated. The author presents the results of a simulation experiment in which
the sizes of the Pearson chi-square goodness of fit test are obtained in two cases: when
the unknown parameters are estimated from grouped data by means of the EM algorithm
(correct procedure) and when original, ungrouped data are used (a wrong but frequently
used procedure).