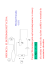Spectral theory for subordinate Brownian motions in half-line

Spectral theory for subordinate Brownian motions in half-line

Spectral theory for subordinate
Brownian motions in half-line
Mateusz Kwa±nicki
Institute of Mathematics and Computer Science
Wrocªaw University of Technology
[email protected]
http://www.im.pwr.wroc.pl/~kwasnicki/
joint project with T. Kulczycki, J. Maªecki and A. Stós
( )
Ÿ1
Introduction
I Xt
symmetric Lévy process;
I
Ψ(ξ) Lévy-Khintchin exponent;
I
τx = inf {t : Xt > x } rst passage time through
x
> 0.
Fluctuation theory (Pecherski-Rogozin formula) gives:
Z ∞Z ∞
1 − Ψλ (ξ)
−ξ x −λt
e
P(τx ∈ dt )dx =
,
ξ
where
0
0
Z ∞
1
ξ
λ
log
dζ .
Ψλ (ξ) = exp
π 0 ξ2 + ζ 2
λ + Ψ(ζ)
In general, inverting the double Laplace transform is dicult.
Ÿ2
Sloshing problem (1/2)
Small, irrotational oscillations of an ideal uid are described by the
sloshing problem:
∆uλ = 0
∂ uλ
∂n
∂ uλ
∂n
inside the container,
=0
at the walls of the container,
= λuλ
on the free surface.
λ spectral parameter related to frequency of the wave.
Dates back to Euler, 1761.
Ÿ2
Sloshing problem (2/2)
Two-dimensional sloshing in innite container with semi-innite dock:
∆uλ (x , y ) = 0,
∂ uλ
∂ y ( x , 0)
∂ uλ
∂ y ( x , 0)
y
< 0;
= 0,
x
< 0;
(Neumann)
= λuλ (x , 0)
x
> 0.
(Steklov )
Solved by Friedrichs and Lewy in 1947 using complex variable methods
and Laplace transform.
Ÿ3
Cauchy process in half-line (1/4)
T. Kulczycki, MK, J. Maªecki, A. Stós
Spectral Properties of the Cauchy Process on Half-line and Interval.
Proc. London Math. Soc. (2010) 101(2) 589622, arXiv:0906.3113.
A slightly modied problem:
∆uλ (x , y ) = 0,
y
< 0;
uλ (x , 0)
x
< 0;
(Dirichlet !)
x
> 0,
(Steklov )
= 0,
∂ uλ
∂ y ( x , 0)
= λuλ (x , 0)
can be solved in a similar manner.
q
d 2 Fλ (x ) = λFλ (x ) for
Fλ (x ) = uλ (x , 0) satises
− dx
2
x
> 0.
Ÿ3
Cauchy process in half-line (2/4)
q
d 2 is the generator of the Cauchy process:
−A = − − dx
2
t
1
Px (Xt ∈ dy ) =
.
2
π t + (y − x )2
Lévy-Khinchin exponent: Ψ(ξ) = |ξ|.
Consider
X
t killed upon leaving half-line D = (0, ∞):
τD = inf {t ≥ 0 : Xt ∈
/ D },
D
t = Xt
D
Xt = ∂
X
when
t
< τD ,
when
t
≥ τD .
−AD , the generator of XtD , agrees pointwise with −A on
Hence,
Fλ (x )
= uλ (x , 0) is the eigenfunction of AD .
D.
Ÿ3
Cauchy process in half-line (3/4)
Theorem (TK+MK+JM+AS, 2010)
The eigenfunctions of AD are given by:
= sin(λx + π8 ) − Gλ (x ),
√ Z ∞
2
ξ
×
Gλ (x ) =
2π 0 1 + ξ 2
Z ∞
1
ξ
1
−λξ x
× exp
log
dζ e
d ξ.
π 0 ξ2 + ζ 2
1+ζ
Fλ (x )
Fλ
yield a generalized eigenfunction expansion of AD .
Formula for transition density of XtD :
Z
2 ∞ −t λ
D
pt (x , y ) =
e
Fλ (x )Fλ (y )d λ.
π 0
Ÿ3
Cauchy process in half-line (4/4)
Theorem (TK+MK+JM+AS, 2010)
Transition density of XtD is given by:
t
1
1
D
−
pt (x , y ) =
π t 2 + (x − y )2 xy
where
Z t q ( s )q ( t −s )
x
y
s + t −s ds ,
0
x
y
Z
ξ
1 ξ
1 ∞
1
q (ξ) =
exp −
log
2
2
2
π1+ξ
π 0 ξ +w
1+w
Theorem (Darling, 1956)
Survival probability is given by
Px (τD ∈ dt ) =
1 t t
f
x
dt .
Remark: Px (τD ∈ dt ) = P0 (τx ∈ dt ).
dw
.
Ÿ4
Cauchy process in interval
In this slide only,
D
= (−1, 1). Then the spectrum of AD is discrete.
Theorem (TK+MK+JM+AS, 2010)
We have λn = n2π − π8 + O ( n1 ). More precisely,
π 1
≤ .
2
8
n
In particular, all eigenvalues are simple.
λn −
nπ
−
Ÿ3
Cauchy process in half-line (3/4)
Theorem (TK+MK+JM+AS, 2010)
The eigenfunctions of AD are given by:
= sin(λx + π8 ) − Gλ (x ),
√ Z ∞
2
ξ
×
Gλ (x ) =
2π 0 1 + ξ 2
Z ∞
1
ξ
1
−λξ x
× exp
log
dζ e
d ξ.
π 0 ξ2 + ζ 2
1+ζ
Fλ (x )
Fλ
yield a generalized eigenfunction expansion of AD .
Formula for transition density of XtD :
Z
2 ∞ −t λ
D
pt (x , y ) =
e
Fλ (x )Fλ (y )d λ.
π 0
Ÿ5
Subordinate Brownian motion in half-line (1/5)
MK, Spectral analysis of subordinate
Submitted 2010, arXiv:1006.0524.
Brownian motions in half-line.
Setting
(A) Xt = B (ηt ) is a subordinate Brownian motion in R;
I Var B = 2t for simplicity;
t
I η is a subordinator;
t
I E(e −ξη ) = e −t ψ(ξ) , where ψ is a Bernstein function;
2
I E(e i ξ X ) = e −t ψ(ξ ) , so that Ψ(ξ) = ψ(ξ 2 );
2
I −A = −ψ(− d ) is the generator of X .
t
dx 2
(B) ψ is a complete Bernstein function.
(C) Technical assumption.
t
t
Conjecture
(C) is superuous.
Ÿ5
Subordinate Brownian motion in half-line (2/5)
Examples
I
Symmetric α-stable process,
Ψ(ξ) = |ξ|α ; 0 < α ≤ 2;
I
Sum of Brownian motion and symmetric α-stable process,
Ψ(ξ) = ξ 2 + |ξ|α , when 0.883... < α < 2;
I
Relativistic
p process,
Ψ(ξ) = ξ 2 + m2 − m.
(Conjectured to include all complete Bernstein subordinators.)
−AD generator of XtD , i.e.
X
t killed upon exiting D = (0, ∞).
Ÿ5
Subordinate Brownian motion in half-line (3/5)
Theorem (MK, 2010): The eigenfunctions of AD are given by:
Z ∞
F (x ) = sin(λx + ϑ ) −
γ (ξ)e −x ξ d ξ,
λ
λ
0
λ
λ
ψ 0 (λ2 )(λ2 − ζ 2 )
d ζ,
log
2
2
ψ(λ2 ) − ψ(ζ 2 )
0 ζ −λ
1
λψ 0 (λ2 )
γλ (ξ) =
Im
×
π
ψ(λ2 ) − ψ + (−ξ 2 )
Z
1 ∞
ξ
ψ 0 (λ2 )(λ2 − ζ 2 )
× exp −
log
d ζ d ξ.
π 0 ξ2 + ζ 2
ψ(λ2 ) − ψ(ζ 2 )
Eigenvalue: ψ(λ2 ).
ϑλ =
1
π
Z
∞
Here ψ + (−ξ) = lim ψ(−ξ + i ε).
ε&0
(This result does not require (C).)
Ÿ5
Subordinate Brownian motion in half-line (4/5)
Wiener-Hopf method (an analytic tool):
I
For λ + A: uctuation theory for Lévy processes,
λ
= Ψλ (−i ξ)Ψ∗λ (−i ξ);
λ + Ψ(ξ)
I
For Ψ(λ) − A: the foregoing spectral theory,
Ψ(λ) − Ψ(ξ)
= Ψ̃λ (−i ξ)Ψ̃∗λ (−i ξ).
λ2 − ξ 2
Problem
Can one obtain the formula for
Fλ
in a probabilistic way?
Ÿ5
Subordinate Brownian motion in half-line (5/5)
Theorem (MK, 2010)
Transition density of XtD is given by
2
R+
t (x , y ) = π
p
∞
Z
Fλ (x )Fλ (y )d λ.
0
Survival probability equals
2
Px (τD > t ) =
π
Z
0
∞
e
−t
ψ(λ2 )
s
Fλ (x )
ψ 0 (λ2 )
dλ
ψ(λ2 )
Ÿ6
Summary (1/3)
First passage time τx through a barrier x > 0 has distribution
s
ψ 0 (λ2 )
d λ,
ψ(λ2 )
0
Z
q
2 ∞ −t ψ(λ2 )
P(τx ∈ dt ) =
e
Fλ (x )
ψ 0 (λ2 )ψ(λ2 ) d λ,
π 0
where
Z ∞
Fλ (x ) = sin(λx + ϑλ ) −
γλ (ξ)e −x ξ d ξ,
0
Z
1 ∞
λ
ψ 0 (λ2 )(λ2 − ζ 2 )
ϑλ =
log
d ζ,
π 0 ζ 2 − λ2
ψ(λ2 ) − ψ(ζ 2 )
1
λψ 0 (λ2 )
γλ (ξ) =
Im
×
π
ψ(λ2 ) − ψ + (−ξ 2 )
Z
1 ∞
ξ
ψ 0 (λ2 )(λ2 − ζ 2 )
× exp −
log
d ζ d ξ.
π 0 ξ2 + ζ 2
ψ(λ2 ) − ψ(ζ 2 )
2
P(τx > t ) =
π
Z
∞
e
−t ψ(λ2 )
Fλ (x )
Ÿ6
Summary (2/3)
1.0
1.0
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
0
2
1.0
4
a = 0.5
6
8
10
0.8
0.6
0.6
0.4
0.4
0.2
0.2
2
4
a = 1.5
2
4
a=1
6
8
10
0
2
4
a=2
6
8
10
1.0
0.8
0
0
6
8
10
P(τa > t ) for the relativistic process (ψ(ξ 2 ) =
p
ξ 2 + 1 − 1)
Ÿ6
Summary (3/3)
For symmetric α-stable process:
√ Z ∞ − t λα
2α
e
Fλ (x )
P(τx > t ) =
d λ,
π
λ
√ Z0 ∞
2α
α
P(τx ∈ dt ) =
λα−1 e −t λ Fλ (x )d λ,
π
0
where
Z ∞
Fλ (x ) = sin(λx + ϑ) −
γ(s )e −λxs ds ,
0
(2 − α)π
,
ϑ=
√8
α
2α sin απ
s
2
γ(s ) =
×
2π
1 + s 2α − 2s α cos απ
2
Z ∞
1
1 − s αw α
1
× exp
log
π 0 1 + w2
1 − s 2w 2
dw
.
Ÿ7
π/2
conjecture
The technical assumption (C) can be proved by showing that
Z ∞
2
s (x + y )
×
2
2
2
2
0 (x + s )(y + s )
Z ∞
1
π
x
y
ψ 0 (s 2 )(t 2 − s 2 )
× exp
dt ds =
.
+ 2
log
2
2
2
2
2
π 0
x +t
y +t
ψ(t ) − ψ(s )
2
Conjecture
This identity holds for any increasing, dierentiable ψ and x , y > 0,
as long as the integral makes sense.
(Strongly supported by numerical experiments.)
Ÿ8
PDEs
Kren correspondence:
b
←→ ψ .
Solution of the spectral problem:
∆uλ (x , y ) + b (y ) ∂∂uyλ (x , y ) = 0,
y
< 0;
uλ (x , 0)
x
< 0;
(Dirichlet)
x
> 0,
(Steklov)
= 0,
∂ uλ
∂ y ( x , 0)
2
= ψ(λ )uλ (x , 0),
satises u (x , 0) = Fλ (x ).
This is because
∂
∂ y u (x , 0)
d )u (x , 0).
= ψ(− dx
2
2
Very few explicit examples known, e.g.
= 1−α
←→ ψ(ξ 2 ) = |ξ|α ;
x
p
b (y ) = −2m
←→ ψ(ξ 2 ) = ξ 2 + m2 − m.
I b (y )
I