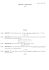1, a dla n 1 (a) f(n +1)=(f(n)) - Informacje dla uzytkowników serwera

1. Rekurencja
Z. 1. Oblicz f (4), jeśli f (0) = 1, f (1) = −1, a dla n ­ 1
(a) f (n + 1) = (f (n))2 + f (n − 1),
(b) f (n + 1) = 2f (n) ,
(c) f (n + 1) = 3f (n), gdy n jest parzyste i f (n + 1) = −3f (n), gdy n jest nieparzyste.
Z. 2. Podać rekurencyjną definicję ciągu (bn ), w której bn jest wyrażone przy pomocy bn−1 . Proszę
pamiętać o warunkach początkowych.
(a) bn = 10n dla n ­ 0, (b) bn = 5 dla n ­ 1, (c) bn = −3n dla n ­ 0.
Z. 3. Zgadnąć i udowodnić indukcyjnie wzór jawny na an , jeżeli
(a) a1 = 3, a2 = −1, an = 2an−1 − an−2 , dla n ­ 3.
(b) a0 = −2, an+1 = − 2a1n , dla n ­ 0.
Ponadto w punkcie (a) wyznaczyć wzór jawny, korzystając z odpowiedniego twierdzenia.
Z. 4. Udowodnić indukcyjnie, że am ­ 2m dla wszystkich wyrazów ciągu (an ), zdefiniowanego rekurencyjnie:
a0 = 2, a1 = 3, an = an−1 + 2an−2 , dla n ­ 2.
Następnie wyznaczyć wzór jawny, korzystając z odpowiedniego twierdzenia.
Z. 5. Ciąg (an ) jest zdefiniowany rekurencyjnie w następujący sposób: a0 = 1, a1 = 3 oraz an =
an−1 + an−2 .
(a) Oblicz a6 .
(b) Korzystając z odpowiedniego twierdzenia, podaj wzór jawny na an .
Z. 6. Ciąg (an ) jest zdefiniowany rekurencuyjnie w następujący sposób: a0 = 1, a1 = 3, a2 = 5 oraz
an = 3an−2 + 2an−3 . Udowodnić, że an > 2n dla n ­ 1.
Z.
 7. Znajdź postać jawną ciągu zadanego równaniem rekurencyjnym:
a0 = 1,



 a = 2,
1

a2


 an = n−1 dla n ­ 2.
an−2
Z. 8. Rozwiąż równanie rekurencyjne:
(
T (2) = 0,
√ T (n) = 2T n + 1 dla n ­ 1,
k
przy czym n jest postaci 22 , gdzie k jest liczbą naturalną.
Z. 9. Niech S0 = {0} oraz Si+1 = Si ∪ {|Si |}. Czym jest suma
∞
[
Si ?
i=0
Z. 10. Niech F (n) oznacza sumę kwadratów pierwszych n liczb naturalnych. Podaj rekurencyjną
definicję F (n).
Z. 11. Dany jest ciąg geometryczny o pierwszym wyrazie a i ilorazie q. Podać rekurencyjną definicję
sumy n pierwszych wyrazów tego ciągu.
Z. 12. Podać rekurencyjną definicję sumy n-tej liczby harmonicznej.
Z. 13. W pewnym mieście jeden człowiek zachorował na grypę. Załóżmy, że każda chora osoba zaraża codziennie 4 zdrowe osoby. Ile będzie chorych n dniach? Podaj rozwiązanie w postaci jawnej
i rekurencyjnej.
Z. 14. Dziecko ma n takich samych klocków. Wrzuca je do pudełka po jednym lub po dwa. Niech ln
oznacza liczbę sposobów, na które może to zrobić (rozpatrujemy odpowiednie ciągi jedynek i dwójek).
Podać rekurencyjną definicję ciagu (ln ).
Z. 15. Podać zależność rekurencyjną na liczbę ciągów długości n utworzonych z liter a i b, w których
żadne dwie litery a nie stoją obok siebie. Następnie podać wzór jawny.
Z. 16. Oprocentowanie lokat w banku wynosi 5% w skali roku. Bank proponuje dwa sposoby gromadzenia kapitału:
1) Na początku wpłacamy 1000zł, odsetki doliczane są do kapitału na końcu każdego roku.
1
2
2) Na koniec każdego roku wpłacamy po 100zł, odsetki też są doliczane do kapitału na końcu każdego
roku (oczywiście na końcu roku bank nie doliczy odsetek od 100zł, które właśnie wpłaciliśmy).
Ile zgromadzimy pieniędzy na każdej lokacie po n latach ? Proszę podać rozwiązanie rekurencyjne dla
każdej osobno.
Na której lokacie zgromadzimy więcej przez 30 lat ?
Z. 17. Przy modyfikacji problemu przenoszenia wież Hanoi i dopuszczeniu czterech iglic zamiast trzech,
liczba Rn ruchów potrzebnych do przeniesienia n krążków wyraża się zależnością:
(1) Hn = 2Hn−1 + 1
(2) Hn = 2Hn−2 + 3
(3) Hn = 2Hn−1 + 3
(4) Hn = 2Hn−2 + 1
Z. 18. Podwójna wieża Hanoi składa się z 2n krążków, po dwa krążki w każdym z n rozmiarów.
Zasady przenoszenia takie jak na wykładzie: mamy trzy pręty, nie można położyć większego krążka na
mniejszy. Ile ruchów trzeba co najmniej wykonać, by przenieść wieżę z jednego pręta na drugi ?
Z. 19. (∗) Każdy chory człowiek zaraża dziennie 2 nowe osoby, po czym po 3 dniach zdrowieje. W
chwili „zero” jest jeden chory człowiek. Niech C(n) oznacza liczbę chorych ludzi po n dniach. Podać
rekurencyjną definicję ciągu C(n).
Z. 20. (∗) Mamy gruby krążek sera i wykonujemy n (n ­ 0) cięć (różnym cięciom odpowiadaja różne
płaszczyzny w przestrzeni) Chcemy otrzymać w ten sposób jak najwięcej kawałków sera.
a) Czy opłaca nam się kroić równolegle ?
b) Na ile maksymalnie kawałków rozpadnie się ser przy 4 cięciach ?
c) Wyznacz Pn – maksymalną liczbę kawałków sera, powstających po n cięciach.