Teoria grafów

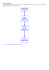
Teoria grafów - zadania
Autor: Szymon Stolarczyk
Spis treści
•
•
•
•
•
Drzewo binarne
Zadanie 1
Zadanie 2
Most
Zadanie 3
Drzewo binarne
W kolejnych zadaniach będziemy używać
terminu „drzewo binarne”. Za drzewo binarne
n-tego stopnia uznajemy graf posiadający jeden
„korzeń”, który ma dwóch „synów”, z których
każdy ma dwóch kolejnych „synów” i tak dalej,
aż do n-tego pokolenia (uznajemy „korzeń” za
pokolenie zerowe). Na następnym slajdie
przedstawione jest drzewo binarne 4-tego
stopnia
Drzewo binarne 4-tego stopnia
Zadanie 1
Należy wyznaczyć wzór na obliczanie ilości
wierzchołków w drzewie binarnym n-tego
stopnia.
Rozwiązanie
Drzewo binarne zerowego stopnia składa się z
jednego wierzchołka. Można zauważyć, że drzewo
n-tego stopnia ma o
więcej wierzchołków niż
drzewo n-1 stopnia. Można więc zapisać ilość
wierzchołków drzewa n-tego stopnia jako:
Korzystając z wzoru na sumę szeregu
geometrycznego możemy przedstawić ten wzór
jako:
W takim razie końcowy wzór to
Zadanie 2
Należy wyznaczyć wzór na obliczanie sum
głębokości wszystkich wierzchołków drzewa
binarnego n-tego stopnia. Za głębokość
wierzchołka uznajemy jego odległość od
korzenia.
Rozwiązanie
Można łatwo zauważyć, że suma głębokości
wierzchołków na poziomie k wynosi
. Jest
tak, gdyż głębokość każdego wierzchołka to k, a
jest ich . W takim razie suma głębokości
wszystkich wierzchołków graf wynosić będzie
Można zauważyć, że
gdzie m jest dowolną liczbą naturalną.
Rozwiązanie c. d.
W takim razie poszukiwany wzór można
przedstawić jako:
Wynika z tego, że wzór na sumę głębokości
wierzchołków
drzewa
binarnego
n-tego
stopnia to
Most
W teorii grafów mostem nazywamy taką
krawędź grafu spójnego, po której usunięciu
przestaje być on spójny.
Zadanie 3
Należy udowodnić, że jeśli w grafie każdy
wierzchołek ma parzysty stopień, to graf ten nie
zawiera mostu.
Rozwiązanie
Załóżmy, że istnieje graf zawierający most, którego
wszystkie wierzchołki mają parzyste stopnie. Po
usunięciu mostu graf ten zostaje podzielony na
dwie części. Zauważmy, że suma stopni w każdej z
części jest nieparzysta, gdyż zawierają one teraz po
jednym nieparzystym wierzchołku. Jest to jednak
niemożliwe, gdyż każda krawędź kończy się w
dwóch wierzchołkach, więc suma każdej spójnej
części musi być parzysta. Udowodniliśmy zatem, że
jeśli w grafie każdy wierzchołek ma parzysty
stopień, to graf ten nie zawiera mostu.