Preskrypt do v.2014Z ćwiczenie nr 5 z 10 (Analiza i przetwarzanie

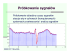
Laboratorium Cyfrowego Przetwarzania Sygnałów
Preskrypt do v.2014Z
ćwiczenie nr 5 z 10 (Analiza i przetwarzanie
sygnałów stochastycznych)
na prawach rękopisu
Lista Autorów
Zakład Teorii Obwodów i Sygnałów
Instytut Systemów Elektronicznych
Wydział Elektroniki i Technik Informacyjnych
Politechnika Warszawska
Uwagi redakcyjne prosimy zgłaszać do: [email protected] tel. 5441
Warszawa, 23 listopada 2014, 1:11
Spis treści
5
Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów)
5.1 Podstawy teoretyczne (sygnały losowe) . . . . . . . . . . . . . . . . . . . . .
5.2 Podstawy teoretyczne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2.1 Sygnały stochastyczne – wstęp . . . . . . . . . . . . . . . . . . . . .
5.2.2 Dyskretne sygnały stochastyczne . . . . . . . . . . . . . . . . . . . .
5.2.3 Klasyczne metody estymacji funkcji autokorelacji i widma mocy . . .
5.2.4 Przetwarzanie stacjonarnych sygnałów stochastycznych przez filtry cyfrowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2.5 Zadania do pracy własnej studenta . . . . . . . . . . . . . . . . . . .
5.3 Dostępny sprzęt i oprogramowanie . . . . . . . . . . . . . . . . . . . . . . .
5.3.1 Skrypty MATLABa® . . . . . . . . . . . . . . . . . . . . . . . . .
5.3.2 Aparatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.4 Eksperymenty do wykonania w laboratorium – sygnały losowe, ich analiza i
przetwarzanie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.4.1 Podstawy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.4.2 Periodogram . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.4.3 Zadania praktyczne – miniprojekty . . . . . . . . . . . . . . . . . . .
2
3
3
3
4
6
9
16
20
21
21
22
22
22
25
26
Ćwiczenie 5
Analiza i przetwarzanie sygnałów
stochastycznych (periodogram, filtracja
szumów)
Opiekun ćwiczenia: ŁM
5.1. Podstawy teoretyczne (sygnały losowe)
5.2. Podstawy teoretyczne
Część teoretyczna na razie jest lekko podrasowaną i nieco okrojoną kopią ze starego
skryptu. Są w niej niespójności i braki – więc może lepiej póki co czytać stary skrypt,
bez rozdziałów o modelowaniu i o filtrze dopasowanym.
Sygnały zespolone
Aktualnie jest to temat dodatkowy, ale warto go szybko przeczytać
Dogłębne rozpatrywanie sygnałów zespolonych wykracza poza ramy tego ćwiczenia1 .
Przyszły inżynier zapewne jednak z takimi sygnałami się zetknie, dlatego bardzo skrótowo
o nich wspomnimy, i we wzorach definicyjnych będziemy uwzględniać mozliwość, że sygnał
jest zespolony. Dla sygnału rzeczywistego Czytelnik raczy po prostu pominąć operator sprzężenia ∗ (bo tym jedynie będą się wyróżniać zapisy dla sygnałów zespolonych).
Sygnały zespolone będą w praktyce występować głównie tam, gdzie badany sygnał jest
przeniesioną do pasma podstawowego kopią sygnału o częstotliwościach radiowych. W ćwiczeniach student taki sygnał otrzyma z cyfrowego odbiornika radiowego USB.
Ciągły sygnał zespolony to matematycznie funkcja czasu mogąca przyjmowac wartości
zespolone. Dyskretny sygnał zespolony to – analogicznie – ciąg próbek mogących przyjmować
wartości zespolone.
W praktyce sygnał zespolony musi być reprezentowany przez dwa rzeczywiste sygnały
ciągłe lub dyskretne, reprezentujące część rzeczywistą i urojoną.
x(n) = xRe (n) + jxIm (n)
1
Głównie z braku czasu :-).
3
(5.1)
4 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 2014-11-23 1:11
Rys. 5.1: Cyfrowy demodulator IQ (kwadraturowy) z jednym przetwornikiem A/C – fragment
schematu układu RTL2832U firmy Realtek, zastosowanego w odbiornikach cyfrowych USB
dostepnych w laboratorium
To dla inżyniera oznacza pewne kłopoty:
– potrzebujemy dwóch możliwie identycznych przetworników C/A, (albo specjalnego układu
w którym próbkuje się jeden sygnał rzeczywisty na częstotliwości pośredniej, a potem, już
cyfrowo, tworzy sygnał zespolony w paśmie podstawowym),
– przetwarzamy dwa razy więcej próbek,
– każde dodawanie zespolone to dwa dodawania rzeczywiste,
– każde mnożenie liczb zespolonych to cztery mnożenia rzeczywiste, plus dodawanie i odejmowanie,
– jak można zgadnąć, współczynniki (np. filtrów) też często będą zespolone.
Najczęściej spotykanym źródłem sygnału zespolonego jest demodulator kwadraturowy w
cyfrowym odbiorniku radiowym – przykład takiego układu pokazano na rys. 5.1. Symbol “I”
oznacza “In-phase” czyli część rzeczywistą sygnału zespolonego, “Q” oznacza “Quadrature”
– czyli część urojoną2 .
5.2.1. Sygnały stochastyczne – wstęp
Co to jest sygnał stochastyczny (losowy)?
Zazwyczaj pojęcia losowości używamy do opisu zjawisk, o których nie mamy pojęcia –
np. z powodu ich olbrzymiej złożoności, albo zależności od przyczyn, których nie możemy
poznać. Na przykład wynik rzutu kostką zależy deterministycznie od mnóstwa czynników
(ruchy powietrza, sposób rzutu …), na które nie mamy wpływu (ani możliwości wystarczająco
dokładnego zmierzenia).
Wynik konkretnego pojedynczego rzutu jest liczbą która może przyjmować sześć wartości,
natomiast teoretyczny twór opisujący wszystkie możliwe rzuty (nieskończenie wiele możliwych rzutów) nazywamy zmienną losową (i wtedy wynik jednego rzutu jest realizacją tej
zmiennej). Intuicyjnie można sobie wyobrazić zmienną losową jako zespół (zbiór) wszystkich
nieskończenie wielu realizacji.
Sygnał losowy (proces stochastyczny) można rozpatrywać analogicznie:
2
Uwaga na możliwość pomyłki – “I” to Re, a “Q” to Im !!!
2014-11-23 1:11 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 5
– realizacją jest tu pojedyncza funkcja czasu ciągłego lub dyskretnego – czyli po prostu sygnał, który jest wynikiem obserwacji (pomiaru, rejestracji); realizacje oznaczamy więc zazwyczaj jako sygnały x(t) czy y[n];
– sygnał losowy jest zespołem (zbiorem) wszystkich takich realizacji – czyli pewnym tworem
teoretycznym, reprezentującym całość zjawiska, z którego takie realizacje maja pochodzić;
sygnały losowe dla odróżnienia od ich realizacji oznaczamy odpowiednimi literami greckimi:
– ξ(t) (ksi – jako odpowiednik “iks”)
– η[n] (eta/ita jako odpowiednik “igrek”)
– ζ[n] (zeta jako odpowiednik “zet”)
– pojedyncza próbka x(t) lub x(n) (wybrana z sygnału x(t) lub x[n] przy ustalonej chwili
czasu t lub n) jest realizacją zmiennej losowej ξ(t) lub ξ(n); w przypadku sygnałów dyskretnych (i dyskretnych sygnałów losowych) warto konsekwentnie stosować konwencję, że
nawiasów kwadratowych [ ] używamy, gdy mówimy o całym sygnale (funkcji), a okrągłych
( ) – gdy mówimy o jednej próbce (wartości funkcji w punkcie).
Studentom zazwyczaj sprawia nieco kłopotu rozróżnienie pomiędzy procesem (sygnałem
losowym) ξ[n], jego realizacją x[n], próbką procesu ξ(n) i realizacją próbki x(n) – ilustrację
tego rozróżnienia pokazano na rys. 5.2. Dla pozbycia się tego kłopotu, usilnie zalecamy Czytelnikowi, aby czytając dalszy tekst usiłował zrozumieć dlaczego w danym miejscu używamy
takiego a nie innego symbolu spośród wymienionych czterech możliwości.
Rys. 5.2: Ilustracja pojęcia: proces stochastyczny – tu na przykładzie procesu (sygnału) z czasem ciągłym
Jeżeli wartości sygnału są liczbami zespolonymi, proces też jest zespolony
ξ[n] = ξRe [n] + jξIm [n]
(5.2)
Jak opisać matematycznie proces stochastyczny?
Zasadniczym opisem zmiennej losowej jest funkcja gęstości prawdopodobieństwa (FGP,
po angielsku – Probability Density Function PDF); funkcja ta (w uproszczeniu) opisuje prawdopodobieństwo przyjęcia przez zmienną konkretnej wartości.
Korzystanie z FGP daje pełną informację o zmiennej losowej, ale jest uciążliwe – dlatego
chętnie stosuje się bardziej syntetyczne opisy w postaci miar liczbowych (tzw. momentów):
– wartości średniej (moment pierwszego rzędu), której interpretacja jest oczywista;
6 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 2014-11-23 1:11
– wariancji (moment centralny drugiego rzędu), która jest miarą rozrzutu wartości zmiennej
losowej wokół jej wartości średniej.
Dla przypomnienia: termin “moment k-tego rzędu” oznacza wartość oczekiwaną
k−tej potęgi zmiennej losowej; jeśli ma przymiotnik “centralny” to oznacza, że przed
obliczeniem go należy odjąć wartość średnią.
Należy pamiętać, że momentami operuje się łatwo, ale nic one nie mówią np. o kształcie
rozkładu prawdopodobieństwa.
Gdy rozpatrujemy sygnał losowy (proces stochastyczny) z czasem dyskretnym sytuacja się
komplikuje.
– Po pierwsze, dla każdego n mamy oddzielną zmienną losową ξ(n); nawet jeśli rozpatrujemy
sygnał o skończonym czasie trwania, zmiennych tych jest wiele, i każda ma swoją FGP oraz
momenty; to oznacza, że każdy moment sygnału losowego jest też sygnałem (na szczęście
już deterministycznym) z tym samym czasem.
– Po drugie, zazwyczaj ważne są nie tylko informacje o tym co dzieje się w danej chwili
czasowej (a więc FGP i momenty każdej próbki z osobna), ale również o zależnościach
między wartościami w kolejnych chwilach czasowych.
Pełnym opisem procesu stochastycznego z czasem dyskretnym jest więc łączna gęstość prawdopodobieństwa – funkcja o tylu wymiarach, ile próbek zawiera nasz sygnał.
Ze względu na uciążliwość analizowania wielowymiarowej łącznej FGP, często uciekamy
się do opisu uproszczonego, w którym badamy wartość oczekiwaną iloczynu próbek z różnych
chwil czasowych: ξ(n) i ξ(m). Jeśli zapiszemy tę wartość jako funkcję czasu (a dokładnie
dwóch zmiennych czasowych: n1 i n2 ), otrzymamy funkcję autokorelacji (ang. autocorrelation
function, ACF).
Na szczęście w wielu zastosowaniach możemy przyjąć, że sygnał losowy jest stacjonarny,
tj. jego właściwości (np. momenty) nie zmieniają się ze zmianą n. Wtedy możemy znaleźć
jedną wartość każdego momentu dla całego procesu, a funkcja autokorelacji zależy od jednego
argumentu – różnicy czasów m = n1 − n2 .
W ogólnym przypadku wyznaczenie tych miar – momentów i funkcji autokorelacji –
wymaga analizowania modelu matematycznego sygnału losowego. Jeśli mówimy o wartości oczekiwanej E( · ), oznacza to uśrednienie statystyczne – a więc po zbiorze wszystkich
możliwych realizacji.
W praktyce często musimy oszacować wartości pewnych parametrów z wyników pomiarowych – np. z zarejestrowanej jednej lub kilku realizacji procesu. Mówimy wtedy, że chcemy
wyestymować te wartości. Metodę uzyskiwania takiej oszacowanej wartości nazywamy estymatorem (np. estymatorem wariancji), a wynik uzyskany dla konkretnego eksperymentu –
estymatą.
5.2.2. Dyskretne sygnały stochastyczne
Pojęcia podstawowe
Będziemy zakładać, że ξ[n] jest w ogólnym przypadku sygnałem zespolonym (5.2).
Jeśli ξ[n] jest sygnałem losowym, to jego momenty rzędu pierwszego i drugiego określają
następujące zależności.
– Wartością średnią (oczekiwaną) sygnału ξ[n] nazywamy deterministyczny ciąg czasowy
2014-11-23 1:11 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 7
µξ [n], którego elementami
µξ (n) = E[ξ(n)] = E[ξR (n)] + jE[ξI (n)] = µξR (n) + jµξI (n)
(5.3)
są wartości średnie kolejnych zmiennych losowych ξ(n).
– Wartością średniokwadratową (mocą średnią) sygnału ξ[n] dla ustalonej wartości n nazywamy wielkość
Pξ (n) = E[ξ(n)ξ ∗ (n)] = E[|ξ(n)|2 ]
(5.4)
gdzie gwiazdka oznacza wielkość sprzężoną3 .
– Wariancją (mocą składowej zmiennej) sygnału ξ[n] dla ustalonej wartości n nazywamy
wielkość
σξ2 (n) = E{[ξ(n) − µξ (n)][ξ ∗ (n) − µ∗ξ (n)]} = E[|ξ(n)|2 − |µξ (n)|2 ]
(5.5)
– Funkcją autokorelacji (ciągiem autokorelacyjnym) sygnału ξ[n] nazywamy wielkość
Rξξ (n1 , n2 ) = E[ξ ∗ (n1 )ξ(n2 )]
(5.6)
– Funkcją autokowariancji (ciągiem autokowariancyjnym) sygnału ξ[n] nazywamy wielkość
Cξξ (n1 , n2 ) = E{[ξ ∗ (n1 ) − µ∗ξ (n1 )][ξ(n2 ) − µξ (n2 )]}
(5.7)
Warto zapamiętać, że wariancja i autokowariancja zdefiniowane są z usunięciem wartości
oczekiwanej, natomiast autokorelacja – bez4 .
Sygnały stacjonarne
Zakładamy, że właściwości statystyczne sygnału ξ[n] nie zmieniają się w czasie, tzn zmienne losowe ξ[n] są dla każdego n opisane tymi samymi FGP (jedno i dwuwymiarowymi). Analizujemy zatem stacjonarne (w szerszym sensie) szeregi czasowe ξ[n], dla których
µξ (n) = µξ = const
Rξξ (n1 , n2 ) = Rξξ (m), m = n2 − n1
(5.8)
Wartość średnia procesu stacjonarnego jest zatem stałą funkcją czasu, a funkcja autokorelacji nie zależy od wyboru chwil czasu n1 i n2 , a jedynie od „odległości” m = n2 − n1
między zmiennymi losowymi ξ(n1 + m) i ξ(n1 ), których powiązania statystyczne (korelację)
analizujemy.
Hipoteza ergodyczna
Wyznaczenie odpowiednich średnich statystycznych (wartości oczekiwanych) jest kłopotliwe, ponieważ rzadko kiedy dysponujemy zbiorami realizacji zmiennych losowych ξ[n]. Najczęściej obserwujemy jedną realizację x[n] sygnału stochastycznego ξ[n] i na tej podstawie
chcemy wnioskować o właściwościach statystycznych procesu ξ[n]. Jesteśmy zatem „skazani”
3
Jak już mówiliśmy, dla sygnałów rzeczywistych operator sprzężenia nie ma znaczenia – można go pominąć,
ale wzór warto zapamiętać w postaci dla sygnałów zespolonych.
4
W wielu tekstach jednak zakłada się z góry, że sygnał ma zerową wartość oczekiwaną, i wtedy autokorelacja
i autokowariancja są tożsame.
8 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 2014-11-23 1:11
na korzystanie z twierdzenia ergodycznego nie sprawdzając jego założeń, a więc zakładamy że
prawdziwa jest hipoteza ergodyczna. Operacje uśredniania w zbiorze realizacji zastępujemy
operacją uśredniania w czasie pojedynczej (dowolnej) realizacji x[n] sygnału stochastycznego
ξ[n].
Stacjonarny sygnał ξ[n] nazywamy ergodycznym (ze względu na wartość średnią i funkcję
autokorelacji) jeśli średnia czasowa
N
X
1
x(n)
N →∞ 2N + 1
n=−N
⟨x[n]⟩ = lim
(5.9)
pewnej (dowolnej) realizacji x[n] procesu ξ[n] i czasowa funkcja korelacji
N
X
1
x∗ (n)x(n + m)
N →∞ 2N + 1
n=−N
ψxx (m) = lim
(5.10)
są równe (z prawdopodobieństwem 1) odpowiednim średnim statystycznym (5.8), tzn
⟨x[n]⟩ = µξ = const


ψxx (m) = Rξξ (m), m = n2 − n1 
(5.11)
Z zależności (5.10) otrzymujemy dla m = 0 średnią moc realizacji x[n]. Moc ta, zgodnie
z (5.11), jest równa średniej mocy sygnału stochastycznego ξ[n].
Gęstość widmowa mocy (widmo mocy)
Będziemy analizować stacjonarne dyskretne sygnały stochastyczne ξ[n] o zerowej wartości
średniej5 µξ = 0. W związku z tym będziemy używali wyłącznie pojęcia autokorelacji, nie
zajmując się autokowariancją.
Jeśliby analizowany sygnał nie spełniał tego założenia (tj. µξ ̸= 0), to można badać
sygnał ξ1 [n] = ξ[n] − µξ , który już ma zerową wartość średnią.
Ponieważ załozylismy stacjonarność sygnału, we wzorze (5.6) mozemy zamiast dwóch
zmiennych czasowych n1 i n2 uzyć ich różnicy:
Rξξ (m) = E {ξ ∗ (n)ξ(n + m)}
(5.12)
Gęstością widmową mocy (widmem mocy) stacjonarnego sygnału dyskretnego ξ[n] nazywamy funkcję Sξξ (θ) do której jest zbieżny szereg Fouriera
Sξξ (θ) =
∞
X
Rξξ (m)e−jmθ
(5.13)
m=−∞
Jeśli proces stochastyczny ξ[n] ma ograniczoną wariancję σξ2 , to szereg (5.13) jest zbieżny (w
sensie średniokwadratowym).
Można więc skrótowo powiedzieć, że widmowa gęstość mocy sygnału jest to transformata
Fouriera jego funkcji autokorelacji (gdyby µξ ̸= 0, trzebaby tu napisać “autokowariancji”).
5
O, właśnie – patrz przypis numer 4.
2014-11-23 1:11 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 9
Widmo mocy Sξξ (θ) stacjonarnego sygnału stochastycznego ξ[n] jest funkcją okresową (o
okresie 2π). Jeśli ξ[n] jest sygnałem rzeczywistym, to S(θ) jest nieujemną (dlaczego?) parzystą funkcją okresową. Jeśli znamy widmo mocy Sξξ (θ) pewnego sygnału ξ[n], to rozwijając
Sξξ (θ) w szereg Fouriera otrzymamy współczynniki rozwinięcia
Rξξ (m) =
1 Zπ
Sξξ (θ)ejmθ dθ
2π −π
(5.14)
określające kolejne próbki funkcji autokorelacji sygnału ξ[n] dla m = 0, ±1, . . ..
Zauważmy, że funkcja autokorelacji Rξξ (m) ((5.12)) dla m = 0 jest wariancją σξ2 dyskretnego procesu stochastycznego (średnią mocą sygnału). Z wzoru (5.14) widać, że dla m = 0
średnią moc sygnału ξ[n] można również wyznaczać w dziedzinie częstotliwości, całkując
funkcję Sξξ (θ) za okres 2π. Funkcja Sξξ (θ) rzeczywiście określa gęstość widmową mocy, tzn
moc sygnału ξ[n] przypadającą na jednostkę unormowanej częstotliwości fn .
5.2.3. Klasyczne metody estymacji funkcji autokorelacji i widma mocy
W wielu zastosowaniach praktycznych właściwości procesu stochastycznego ξ[n] często musimy oceniać na podstawie znajomości tylko jednej jego realizacji, obserwowanej w skończonym przedziale czasu. Powstaje więc problem estymacji wielkości µξ , σξ2 , Rξξ (m), Sξξ (θ) na
podstawie znajomości fragmentu jednej realizacji x[n], n = 0, 1, . . . , N − 1, procesu stochastycznego ξ[n]. Aby było to możliwe, trzeba założyć, że analizowany proces ξ[n] jest stacjonarny i ergodyczny.
Jeśli dla pewnej realizacji x[n], −∞ < n < ∞, procesu stochastycznego jest znana tylko
skończona liczba próbek x(0), x(1), . . . , x(N − 1), tzn. jest znany sygnał
x0 [n] = x[n]g[n], −∞ < n < ∞
(5.15)
gdzie g[n] jest oknem prostokątnym, to w tzw klasycznych metodach estymacji często stosuje
się następujące estymatory
– estymator wartości średniej – por. (5.9)
µ̂ξ =
−1
1 NX
x(n)
N n=0
(5.16)
– estymator wariancji sygnału o nieznanej wartości średniej (wartości średniej nie znamy,
więc wykorzystujemy jej estymatę µ̂ξ )
σ̂ξ2 =
−1
1 NX
[x∗ (n) − µ̂∗ξ ][x(n) − µ̂ξ ]
N n=0
(5.17)
– estymator funkcji autokorelacji sygnału stochastycznego o zerowej wartości średniej – por. (5.10)
R̂ξξ (m) =













X
1 N −|m|−1
x∗ (n)x(n + m) dla 0 ¬ m ¬ N − 1
N n=0
−1
1 NX
x∗ (n)x(n + m)
dla − (N − 1) ¬ m < 0
N n=|m|
(5.18)
10 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 2014-11-23 1:11
– estymator widma mocy – por. (5.13)
Ŝξξ (θ) =
N
−1
X
R̂ξξ (m)e−jmθ
(5.19)
m=−(N −1)
Zauważmy, że dla różnych realizacji x[n] procesu stochastycznego ξ[n] otrzymamy różne
wartości estymat (5.16) i (5.17) oraz różne przebiegi funkcji (5.18) i (5.19).
Chcielibyśmy, aby te wyniki możliwie dobrze przybliżały prawdziwe wartości poszukiwanych parametrów procesu ξ[n], ale niestety wielkości µ̂ξ i σ̂ξ2 same też są zmiennymi losowymi,
a R̂ξξ (m) i Ŝξξ (θ) – procesami stochastycznymi.
5.2.3.1. Dokładność estymacji
Przypuśćmy, że pewien parametr α procesu stochastycznego oceniamy za pomocą estymatora α̂. Chcielibyśmy ocenić, jak bardzo “prawdziwy” jest wynik takiej oceny dokonanej z
pojedynczej realizacji procesu.
Skoro taka estymata jest zmienną (lub funkcją) losową, można badać jej wartość oczekiwaną i wariancję. To, jak bardzo wartość oczekiwana estymaty różni się od wartości faktycznej
parametru, nazywamy obciążeniem estymatora. Jak bardzo rozrzucone są estymaty dokonane z różnych realizacji określamy za pomocą wariancji (lub wartości średniokwadratowej)
estymatora.
Obciążenie estymatora α̂ definiujemy jako różnicę
B = α − E[α̂]
(5.20)
między wartością parametru α i wartością oczekiwaną estymatora.
Miarą skupienia estymatora α̂ wokół wartości przeciętnej E[α̂] jest wariancja estymatora
var[α̂] = σα̂2 = E {[α̂∗ − E(α̂)∗ ][α − E(α̂)]}
(5.21)
Estymator o małym obciążeniu może mieć dużą wariancję (i na odwrót). Jeśli chcemy jedną liczbą określić jakość estymatora, oceniamy ją za pomocą jego błędu średniokwadratowego
h
i
E |α̂ − α|2 = B 2 + σα̂2
(5.22)
„Dobry” estymator powinien mieć zerowe (lub bliskie zeru) obciążenie i małą wariancję.
Są to niestety często sprzeczne wymagania. Często dodatkowo wymaga się, aby estymator α̂
był zgodny, tzn. aby ze wzrostem liczby obserwacji N zarówno jego obciążenie jak i wariancja
dążyły do zera. Poszukiwanie „dobrych” estymatorów i ocena ich parametrów jest trudnym
problemem; rozwiązania analityczne są znane tylko dla stosunkowo prostych przypadków (np.
dla gaussowskich procesów stochastycznych).
5.2.3.2. Obciążenie i wariancja klasycznych estymatorów
Jeśli ξ[n] jest gaussowskim stacjonarnym procesem stochastycznym, to można wykazać, że
estymator (5.16) wartości średniej jest nieobciążony, a jego wariancja jest równa σξ2 /N , gdzie
σξ2 jest wariancją procesu ξ[n]. Z kolei estymator wariancji (5.17) procesu stochastycznego
2014-11-23 1:11 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 11
ξ[n] jest obciążony ponieważ B = σξ2 /N , a jego wariancja var[σ̂ξ2 ] jest proporcjonalna do
1/N – jest to więc estymator zgodny.
Przedstawione pojęcia zastosujemy do oceny jakości estymacji funkcji autokorelacji Rξξ [m]
i widma mocy Sξξ (θ) gaussowskich sygnałów ξ[n] o zerowej wartości średniej.
Obciążenie estymatora (5.18) funkcji autokorelacji Rξξ (m) jest opisane zależnością
B=
|m|
Rξξ (m)
N
(5.23)
a jego wariancję dla N ≫ m w przybliżeniu określa wzór
var[R̂ξξ (m)] ∼
=
∞ h
i
1 X
2
Rξξ
(r) + Rξξ (r + m)Rξξ (r − m)
N r=−∞
(5.24)
Estymator (5.18) jest więc:
– zgodny, bo dobierając odpowiedni duże N możemy dowolnie zmniejszyć obciążenie i wariancję,
– obciążony, bo obciążenie nie jest równe zeru – szczególnie w pobliżu końców przedziału
−N . . . N jest ono bardzo duże.
Podsumowując, ten estymator można stosować z powodzeniem dla wartości m w rozsądnej
odległości od zera.
Do estymacji widma mocy Sξξ (θ) sygnału stochastycznego ξ[n] bardzo często stosuje się
estymator (5.19) – czyli transformatę Fouriera estymaty funkcji autokorelacji. Wartość średnią
tego estymatora określa wzór
E[Ŝξξ (θ)] =
N
−1
X
N − |m|
Rξξ (m)e−jmθ
N
m=−(N −1)
(5.25)
a wariancja estymatora Ŝξξ (θ) jest opisana zależnością


"
sin N θ
2
var [Ŝξξ (θ)] = Sξξ
(θ) 1 +

N sin θ
#2 

(5.26)

Wnikliwy Czytelnik zauważy w obu tych wzorach wpływ faktu, że funkcja autokorelacji jest
estymowana z fragmentu sygnału, uciętego oknem prostokątnym:
– N −|m|
to okno Bartletta (trójkątne) – czyli splot dwóch okien prostokątnych
N
– znajomy składnik w wariancji – kwadrat widma okna prostokątnego.
Estymator Ŝξξ (θ) ma jednak poważne wady:
– jego wariancja jest proporcjonalna do kwadratu estymowanego widma mocy (czyli, w
uproszczeniu, można się spodziewać błędów porównywalnych z wartością samego widma!)
– jest obciążony,
– nie jest zgodny – zwiększanie długości realizacji niewiele pomoże.
Okazuje się jedna, że po pewnych modyfikacjach jest on całkiem użyteczny; spróbujemy
pokazać, jak poradzić sobie z w/w problemami.
12 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 2014-11-23 1:11
Obciążenie estymatora
Wartość średnia (5.25) estymatora Ŝξξ (θ) jest widmem iloczynu funkcji Rξξ [m]g[n], gdzie
g[n] =

 N −|m|
N

0
dla
|m| < N
dla pozostałych
m
(5.27)
jest oknem Bartletta (trójkątnym). Wynika stąd wniosek: wartość średnia estymatora widma
mocy E[Ŝξξ (θ)] jest splotem nieznanego widma mocy Sξξ (θ) z widmem okna Bartletta
G e
jθ
"
1 sin(N θ/2)
=
N
sin θ/2
#2
(5.28)
a więc
1 Zπ
Sξξ (η)G ej(θ−η) dη
(5.29)
2π −π
Oznacza to dość znajomą (i niezbyt straszną) sytuację – widmo jest nieco uśrednione (na
szerokość głównego listka widma okna) i mogą być zauważalne listki boczne.
h
i
E Ŝξξ (θ) =
Wariancja estymatora
Wariancja rozważanego estymatora jest ogromna. Jak można zmniejszyć wariancję wielkości losowych? Zazwyczaj odpowiedzią jest uśrednianie kilku “pomiarów”. Takie podejście
pokażemy za chwilę – warto tylko zauważyć, że suma we wzorze (5.19) nie powoduje uśredniania; dlatego zwiększanie N nie zmniejsza zauważalnie wariancji.
Periodogram
Zauważmy, że estymator funkcji autokorelacji (określony wzorem (5.18)) jest po prostu
splotem sygnału x∗ (n) z sygnałem x(−n) przemnożonym przez stały czynnik. Tak więc
R̂ξξ [m] =

 1 x∗ [m] ∗ x[−m],

N
|m| ¬ N − 1
0,
|m| > N − 1
(5.30)
gdzie symbol ∗ oznacza splot.
Estymator (5.19) widma mocy jest transformatą Fouriera funkcji (5.18) lub, co jest równoważne, transformatą Fouriera splotu (5.30). Estymator Ŝξξ (θ) widma mocy jest zatem (z
dokładnością do mnożnika 1/N ) iloczynem transformaty Fouriera
∗
jθ
X (e ) =
N
−1
X
x∗ (n)e−jnθ
(5.31)
n=0
„wycinka” realizacji x∗ [n], n = 0, 1, . . . , N − 1, procesu stochastycznego ξ ∗ [n] i transformaty
Fouriera X1 (ejθ ) sygnału x1 [n] = x[−n], różnego od zera dla n = 0, −1, . . . , −(N − 1). Tak
więc
X1 (ejθ ) =
0
X
n=−(N −1)
x1 (n)e−jnθ =
N
−1
X
n=0
x1 (−n)ejnθ =
N
−1
X
[x∗ (n)e−jnθ ]∗
n=0
(5.32)
2014-11-23 1:11 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 13
Wielkość (5.32) jest sprzężona z (5.31), tzn. X1 (ejθ ) = X(ejθ ), a więc ostatecznie otrzymujemy bardzo ważną zależność
1
(5.33)
Ŝξξ (θ) = |X(ejθ )|2
N
zwaną periodogramem.
Estymacja widma mocy sygnału stochastycznego ξ[n] sprowadza się do wyznaczenia (za
pomocą DTF realizowanej szybkimi algorytmami FFT) kwadratu widma amplitudowego |X(ejθ )|
„wycinka” realizacji x[n], n = 0, 1, . . . , N − 1, tego procesu. Estymując widmo mocy za pomocą periodogramu pomija się etap estymacji funkcji autokorelacji – por. (5.18) i (5.19).
Do szybkiej estymacji funkcji autokorelacji (5.18) również korzysta się z periodogramu.
Wyznaczając ODTF kwadratu modułu widma (dokładnie |X(ejθ )|2 /N ) dla dyskretnych wartości unormowanej pulsacji θ otrzymamy estymator R̂ξξ (m).
Uwaga. Stosując DTF i ODTF do obliczania splotu, tzn. estymatora funkcji korelacji (autokowariancji), należy zachować dużą ostrożność przy ustalaniu wymiaru transformaty. Próbkowanie widm X ∗ (ejθ ) i X1 (ejθ ) sygnałów x∗ (n) i x1 (n) powoduje bowiem okresowe przedłużenie sygnałów, i w konsekwencji obliczymy splot funkcji okresowych (splot cykliczny).
Aby uzyskać splot liniowy (dla sygnałów o skończonym czasie trwania) tą metodą, musimy
odpowiednio uzupełnić sygnały zerami, aby splot cykliczny był równy liniowemu.
Uśrednianie periodogramów – procedura Bartletta
Z poprzednich rozważań wynika, że technika estymacji widma mocy i funkcji korelacji
procesu stochastycznego ξ[n] jest bardzo prosta – wystarczy wyznaczyć widmo amplitudowe
|X0 (ejθ )| analizowanego fragmentu x0 [n] jednej z realizacji x[n] (tzn. sygnału deterministycznego), obliczyć kwadrat tego widma i podzielić przez N . Funkcję korelacji procesu ξ[n] również estymuje się za pomocą periodogramu – wystarczy wyznaczyć transformatę odwrotną
periodogramu.
Jak więc wykorzystać tę efektywną metodę, i uporać się z problemem olbrzymiej wariancji
estymatora widma mocy?
W celu zmniejszenia wariancji estymatora (5.18) powszechnie stosuje się uśrednianie pewnej liczby niezależnych periodogramów (procedura Bartletta). W procedurze tej ciąg danych
x[n] o długości N (n = 0, 1, . . . , N − 1) dzieli się na K segmentów zawierających M próbek
(N = KM ) i dla każdego i-tego segmentu wyznacza się periodogram Ŝi (θ). Jeśli wartości
funkcji autokorelacji Rξξ [m] sygnału ξ[n] są małe dla m > M , to można uznać, że poszczególne periodogramy Ŝi (θ) są nieskorelowane, a więc ich uśrednienie powinno zmniejszyć wariancję wyniku.
Estymator ŜBξξ (θ) jest więc tworzony jako średnia arytmetyczna poszczególnych periodogramów, tzn
K
1 X
Ŝi (θ)
(5.34)
ŜBξξ (θ) =
K i=1
Zróbmy rachunek zysków i strat:
– uśredniając wyniki z K segmentów zmniejszyliśmy wariancję K razy,
– ponieważ segment jest K razy krótszy od całego dysponowanego fragmentu realizacji,
zwiększyło się obciążenie estymatora: mniej danych uśredniamy obliczając pojedynczy periodogram, i używamy krótszego okna (a więc ma ono szerszy listek główny widma).
14 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 2014-11-23 1:11
Jeśli mamy ustaloną długość danych N , konieczny jest – jak widać – kompromis między wyborem liczby segmentów K i ich długością M .
Uśrednianie zmodyfikowanych periodogramów – procedura Welcha
Pamiętamy z poprzednich rozważań, że rozpatrywany estymator jest obciążony poprzez
splot wyniku z widmem okna Bartletta. W konkretnym zastosowaniu możemy natknąć się
na problem zbyt wysokich listków bocznych tego okna. Wtedy przychodzi nam z pomocą
procedura Welcha – uśrednianie zmodyfikowanych6 periodogramów.
Okno oczywiście stosujemy do segmentów danych w dziedzinie czasu i obliczamy zmodyfikowane periodogramy cząstkowe
i
(θ)
ŜW
1
=
MF
2
M −1
X
i
−jnθ ,i
x
(n)g(n)e
= 1, 2, . . . , K
(5.35)
n=0
każdego z K segmentów o długości M (dla liczby danych N = M K), a następnie wyznacza
się estymator uśredniony
K
1 X
i
ŜW ξξ (θ) =
ŜW
(θ)
(5.36)
K i=1
Należy podkreślić, że w zależności (5.35) występuje czynnik normujący (energetyczny)
−1
1 MX
F =
g 2 (n)
M n=0
(5.37)
który jest niezbędny dla zapewnienia asymptotycznej nieobciążalności (gdy K → ∞) estymatora (5.36) – okno na swych skrajach zmniejsza wartości próbek, więc nie uwzględniamy
całej energii z badanego fragmentu danych.
Jeśli segmenty danych nie zachodzą na siebie (rys. 5.3) to wariancja estymatora (5.35)
jest taka sama jak estymatora (5.34). Występuje więc pożądany efekt wygładzenia estymatora
widma mocy, jednak kosztem zmniejszenia rozróżnialności widmowej.
Aby uwzględnić “zmarnowane” próbki ze skrajnych części okna, można zastosować zachodzące na siebie segmenty danych (rys. 5.3) co powoduje dodatkowe zmniejszenie wariancji
estymatora (mamy więcej segmentów. Segmenty co prawda są nieco skorelowane – ale najważniejsze próbki (ze środka okna) jednego segmentu wchodzą do drugiego z dużo mniejszą
wagą). Oznacza to, że wariancja zmniejsza się, ale niekoniecznie aż K-krotnie.
Wyznaczanie estymatora funkcji autokorelacji
Estymator (5.18) funkcji autokorelacji procesu stochastycznego ξ[n] o zerowej wartości
średniej wyznacza się za pomocą DTF, obliczając widmo (5.31) fragmentu realizacji x[n],
n = 0, 1, . . . , N − 1, tego procesu, a następnie wyznacza
się odwrotną dyskretną transfor
2
jθk matę Fouriera kwadratu widma amplitudowego X(e ) unormowanego względem N –
por. (5.33). Z zależności (5.23) i (5.24) wynika, że obciążenie i wariancję tego estymatora można zmniejszyć przez zwiększenie liczby próbek N analizowanego fragmentu realizacji
x[n] procesu ξ[n]. Powstaje więc problem techniczny związany z zastosowaniem DTF i ODTF
6
W przetwarzaniu sygnałów słowo “zmodyfikowany” często oznacza “ucięty oknem innym niż prostokątne”.
2014-11-23 1:11 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 15
Rys. 5.3: Ilustracja podziału bloku danych na segmenty nie zachodzące na siebie (a) i zachodzące na siebie (b).
do obliczania splotu x∗ [n] ∗ x[−n] dla dużych wartości N – por. (5.30). Ustalenie wymaganej liczby N próbek sygnału x[n] zależy od narzuconej dokładności estymacji interesujących
eksperymentatora próbek funkcji Rξξ (m), m = 0, 1, . . . , M − 1.
Jeśli stosujemy DTF i ODTF do estymacji M pierwszych próbek funkcji autokorelacji
procesu ξ[n], to sygnał x[n] zawierający N próbek wystarczy uzupełnić M − 1 zerami (zniekształcenia „interferencyjne” wynikające z obliczania splotu cyklicznego wystąpią dopiero dla
m ­ M ). Obliczamy L = N + M − 1 punktową dyskretną transformatę Fouriera X[k] ciągu
L-punktowego, a następnie wyznaczamy L-punktową ODTF z wielkości |X(k)|2 otrzymując
(po podzieleniu przez N ) próbki funkcji R̂ξξ [m] dla m = 0, 1, . . . , M − 1. Dla zapewnienia
wystarczająco dokładnej estymacji należy spełnić warunek N ≫ M .
Jeśli N jest duże (rzędu kilku lub kilkunastu tysięcy), to obliczanie L = N +M −1 – punktowej DTF i ODTF staje się trudne obliczeniowo lub wręcz niemożliwe. W takim przypadku
procedura obliczeniowa jest następująca. Ponieważ x[n] = 0 dla n < 0 i n ­ N , to górny
wskaźnik w sumie (5.18) można zastąpić przez N − 1 i estymator R̂ξξ [m] zapisać w postaci
sumy K estymatorów (m = 0, 1, . . . , M − 1):
1
R̂ξξ (m) =
N
"M −1
X
∗
x (n)x(n + m) +
n=0
+ ... +
2M
−1
X
n=M
KM
X−1
x∗ (n)x(n + m) + . . . +

(5.38)
∗
x (n)x(n + m)
n=(K−1)M
gdzie N = KM . Do wyznaczenia „splotów cząstkowych” x∗ [n] ∗ x[−n] występujących
w (5.38) można skorzystać z L1 = 2M − 1 punktowej DTF i ODTF. Wykonując K obliczeń tego typu, po ich zsumowaniu otrzymamy R̂ξξ [m] dla m = 0, 1, . . . , M − 1.
16 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 2014-11-23 1:11
−→realizacje
realizacje−→
proces
ξ[n]
x1 [n] −→
−→ y1 [n]
x2 [n] −→ H(z) −→ y2 [n]
...
−→
−→
proces
η[n]
...
Rys. 5.4: Przetwarzanie sygnału stochastycznego przez filtr cyfrowy
5.2.4. Przetwarzanie stacjonarnych sygnałów stochastycznych przez filtry cyfrowe
Metody opisu układów dyskretnych w dziedzinie czasu i częstotliwości były już częściowo
omawiane w poprzednich dwóch ćwiczeniach. Jednym z istotnych zadań tego ćwiczenia jest
analiza i obserwacja sygnałów stochastycznych przetwarzanych przez filtry cyfrowe.
Przetwarzanie sygnałów stochastycznych
Załóżmy, że stacjonarny i ergodyczny sygnał stochastyczny ξ[n] o wartości średniej µξ
i wariancji σξ2 jest przetwarzany przez filtr cyfrowy o transmitancji H(z). W wyniku przetwarzania poszczególnych realizacji x1 [n], x2 [n], . . ., procesu ξ[n] otrzymamy na wyjściu filtru
sygnały y1 [n], y2 [n], . . ., będące realizacjami pewnego procesu stochastycznego η[n].
Mówimy wówczas, stosując skrót myślowy, że sygnał stochastyczny ξ[n] został przetworzony przez układ o transmitancji H(z) w inny sygnał stochastyczny η[n]. W praktyce inżynierskiej może nas interesować wartość średnia µη i wariancja ση2 procesu η[n], najczęściej
jednak chcemy znać funkcję autokorelacji Rηη [m] (lub autokowariancji Cηη [m]) i widmo mocy Sηη (θ) sygnału stochastycznego η[n].
Niekiedy interesuje nas również wzajemne widmo mocy Sξη (θ) między sygnałem wejściowym ξ[n] i wyjściowym η[n] lub funkcja kowariancji wzajemnej Cξη [m].
Można wykazać, że parametry i funkcje opisujące sygnały stochastyczne na wejściu i wyjściu układu opisanego rzeczywistą odpowiedzią impulsową h[n] (transmitancją H(z)) są powiązane następującymi zależnościami:
– wartość średnia procesu η[n] na wyjściu układu
µη = µξ
∞
X
h(n) = µξ H(ejθ )|θ=0
(5.39)
n=−∞
gdzie µξ jest wartością średnią stacjonarnego procesu ξ[n] na wejściu,
– funkcja autokorelacji procesu η[n]
Rηη (m) =
∞
X
Rξξ (m − i)v(i)
(5.40)
h(k)h(k + i)
(5.41)
i=−∞
gdzie
v(i) =
∞
X
k=−∞
a Rξξ [m] jest funkcją autokorelacji stacjonarnego procesu wejściowego ξ[n],
2014-11-23 1:11 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 17
– funkcja korelacji wzajemnej między sygnałem wejściowym ξ[n] i wyjściowym η[n]
∞
X
Rξη (m) =
h(k)Rξξ (m − k)
(5.42)
k=−∞
Zauważmy, że wielkość v(i) określona przez (5.41) jest splotem odpowiedzi impulsowej
h[n] ze swoim zwierciadlanym odbiciem h[−n], a wzór (5.40) jest splotem wielkości Rξξ [i]
i v[i]. Natychmiast (dlaczego?) wynika stąd ważna zależność między widmami mocy procesów ξ[n] i η[n]
Sηη (θ) = Sξξ (θ)V (ejθ )
(5.43)
a ponieważ
V (ejθ ) = H(ejθ )H(e−jθ ) = |H(ejθ )|2
(5.44)
Sηη (θ) = Sξξ (θ)|H(ejθ )|2
(5.45)
więc
Widmo mocy Sηη (θ) sygnału wyjściowego η[n] jest iloczynem widma mocy Sξξ (θ) sygnału
wejściowego ξ[n] i kwadratu charakterystyki amplitudowej |H(ejθ )| układu.
Podobnie otrzymamy ze splotu (5.42) wzajemne widmo mocy sygnałów ξ[n] i η[n]:
Sξη (θ) = Sξξ (θ)H(ejθ )
(5.46)
Wzór (5.46) jest podstawą do estymacji charakterystyki amplitudowo-fazowej nieznanego układu na podstawie estymowanego widma mocy sygnału wejściowego i estymowanego wzajemnego widma mocy między sygnałem wejściowym i wyjściowym badanego układu.
Przykład 5.1. Przypuśćmy, że przyczynowy filtr cyfrowy o transmitancji
H(z) =
b0
1 + a1 z −1 + a2 z −2
(5.47)
gdzie b0 , a1 , a2 są rzeczywistymi parametrami, został pobudzony w chwili n = 0 szumem
białym ξ[n] = w[n] o zerowej wartości średniej i wariancji σw2 .
Zmienne losowe w(n1 ) i w(n2 ) procesu w[n] są dla n1 ̸= n2 nieskorelowane, a funkcja
autokorelacji tego procesu jest (jak dobrze wiemy) opisana zależnością


Rww [m] = σw2 δ[m] = 
σw2
dla m = 0
0
dla m ̸= 0
(5.48)
Widmo mocy szumu białego jest więc stałe, mamy bowiem – por. (5.19)
Sww (θ) =
∞
X
Rww (m)e−jmθ = σw2
(5.49)
n−−∞
filtr jest pobudzony stacjonarnym sygnałem stochastycznym w[n] w chwili n = 0, powstaje
więc pytanie czy sygnał wyjściowy η[n] jest stacjonarny dla n ­ 0. Intuicja podpowiada, że
odpowiedź na to pytanie jest negatywna – w chwili włączenia pobudzenia w układzie powstają stany przejściowe, które dla filtru stabilnego zanikają do zera gdy n → ∞. Można więc
przypuszczać, że sygnał η[n] na wyjściu układu będzie stacjonarny dopiero po odpowiednio
18 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 2014-11-23 1:11
długim czasie od momentu włączenia pobudzenia. Sprawdźmy nasze przypuszczenie obliczając wariancję sygnału wyjściowego. Sygnał wyjściowy η[n] opisuje splot
η[n] =
n
X
h(k)ξ(n − k)
(5.50)
k=0
gdzie h[k] jest odpowiedzią impulsową przyczynowego filtru cyfrowego o transmitancji (5.47)
– przypominamy, że warunek przyczynowości h[n] = 0 dla n < 0 oznacza w dziedzinie
częstotliwości holomorficzność transmitancji H(z) w obszarze |z| ­ R. Wariancję ση2 sygnału
wyjściowego opisuje zależność – por. (5.5)
ση2 (n) = E[η(n)η(n)]
(5.51)
z której po wstawieniu (5.50) otrzymujemy
n X
n
X
ση2 (n) = E[
=
h(k)ξ(n − k)h(i)ξ(n − i)] =
i=0 k=0
n X
n
X
h(k)h(i)E[ξ(n − k)ξ(n − i)]
(5.52)
i=0 k=0
Ponieważ pobudzeniem układu jest szum biały ξ[n] = w[n] o funkcji autokorelacji (5.48) więc
wyrażenie

 σ2
dla k = i
w
(5.53)
E[ξ(n − k)ξ(n − i)] =
0
dla k ̸= i
i nie zależy od czasu n-proces wejściowy jest z założenia stacjonarny. Wstawiając (5.54)
do (5.53) otrzymamy ostatecznie
ση2 (n) = σw2
n
X
h2 (i)
(5.54)
i=0
Potwierdza się nasze wcześniejsze przypuszczenie, że sygnał wyjściowy η[n] jest niestacjonarny – jego wariancja ση2 (n) jest funkcją czasu (wariancja zmiennych losowych η[n1 ] i η(n2 )
jest różna dla n1 ̸= n2 ). Dla dostatecznie dużych n, gdy można przyjąć zaniknięcie do zera
stanu przejściowego otrzymujemy dobrze znany wzór (filtr przyczynowy)
ση2 = σξ2
∞
X
h2 (i)
(5.55)
i=0
wynikający zresztą z (5.40) dla m = 0. Korzystając z równości Parsevala
∞
X
i=0
h2 (i) =
1 Zπ
|H(ejθ )|2 dθ
2π −π
(5.56)
nieskończoną sumę występującą w (5.56) można również wyznaczyć poprzez całkowanie charakterystyki energetycznej filtru (kwadratu charakterystyki amplitudowej A(θ) = |H(ejθ )|).
Pamiętajmy: analiza korelacyjna i widmowa sygnałów stochastycznych otrzymanych na
wyjściu filtru zakłada stacjonarność procesu stochastycznego η[n]. Oznacza to wyeliminowanie stanów przejściowych – nie uwzględnienie w analizie pierwszych kilkudziesięciu (kilkuset) próbek sygnału wyjściowego. Liczba odrzuconych próbek zależy od szybkości zanikania
odpowiedzi impulsowej układu.
2014-11-23 1:11 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 19
Jeśli przyjąć, że stabilny filtr cyfrowy został pobudzony w momencie „nieskończenie odległym” od chwili rozpoczęcia obserwacji sygnału wyjściowego, to można przyjąć, że η[n]
jest sygnałem stacjonarnym, którego widmo mocy, zgodnie z (5.45), opisuje zależność
2
Sηη (θ) = σww
|H(ejθ )|2
(5.57)
Widmo mocy Sηη (θ) sygnału wyjściowego jest kształtowane przez przebieg charakterystyki
amplitudowej filtru; przebieg ten zależy z kolei od położenia biegunów transmitancji (5.47).
W procesie przejścia szumu białego przez filtr otrzymaliśmy na wyjściu tzw. szum kolorowy tzn skorelowany sygnał η[n], którego funkcję autokorelacji Rηη [m] otrzymamy obliczając
odwrotną transformatę Fouriera widma mocy Sηη (θ) – rozwijając okresową funkcję Sηη (θ)
w szereg Fouriera. Fakt, że z białego (nieskorelowanego) szumu otrzymano sygnał skorelowany nie powinien dziwić, narzucono bowiem (w wyniku przetwarzania sygnału przez filtr)
związki funkcyjne między poszczególnymi próbkami, opisane równaniem różnicowym
y(n) = b0 x(n) − a1 y(n − 1) − a2 y(n − 2)
wynikającym z (5.47).
(5.58)
20 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 2014-11-23 1:11
5.2.5. Zadania do pracy własnej studenta
Podobne zadania mogą znaleźć się na wejściówce. Nie dotyczy to zadań oznaczonych tu jako
”trudne”.
1) Rozważ dyskretny szum ξ[n] biały, gaussowski, o wartości średniej µ = 0 i wariancji
2
σ = 1. Jakie jest jego odchylenie standardowe? Jakie jest jego widmo gęstości mocy? Naszkicuj jego funkcję autokorelacji.
Szum wzmocniono trzykrotnie (pomnożono każdą próbkę przez 3). Jak zmieniła się:
– wartość średnia?
– odchylenie standardowe?
– wariancja?
2) Dyskretny szum ξ[n] biały, gaussowski, o wartości średniej µ = 0 i wariancji σ 2 = 1
przechodzi przez układ (filtr) opisany równaniem różnicowym y(n) = x(n) + x(n − 1).
Wyznacz właściwości sygnału na wyjściu filtru:
–
–
–
–
wartość średnią,
wariancję,
widmo gęstości mocy,
funkcję autokorelacji.
Wskazówka: Przy obliczeniu wariancji najprościej zauważyć, że kolejne próbki w(n) są niezależnymi zmiennymi losowymi, i przypomnieć sobie skutki sumowania takich zmiennych
Jak zmienią się odpowiedzi, gdy y(n) = x(n) − x(n − 1)?
3) Podobny jak w poprzednim zadaniu sygnał przechodzi przez kaskadę7 dwóch filtrów
(weź do analizy np. te z poprzedniego zadania). Znowu wyznacz właściwości sygnału. Uważaj
– sygnał na wejściu drugiego filtru już nie jest szumem białym!
4) Obliczanie splotu we wzorze na estymatę funkcji autokorelacji jest kosztowne obliczeniowo. Jak wykorzystać do tego DTF i ODTF (a właściwie FFT i IFFT)?
5) Czym rózni się widmo sygnału (deterministycznego) x[n] i x[−n] (załóż, że x[n] jest
sygnałem rzeczywistym)?
6) Kiedy można z jednej realizacji sygnału wnioskować o jego właściwościach statystycznych? Czy i jak można sprawdzić ten warunek?
7) Widmowa gęstość mocy pewnego sygnału ma kształt prostokątny od −θg do +θg . Naszkicuj funkcję autokorelacji sygnału.
8) Przez układ liniowy i stacjonarny o nieznanej odpowiedzi impulsowej przepuszczono
szum biały ξ[n] ottrzymując sygnał wyjściowy η[n].
a) Co można powiedzieć o odpowiedzi impulsowej i transmitancji układu, analizując tylko
sygnał wyjściowy?
b) Co można powiedzieć o odpowiedzi impulsowej i transmitancji układu, analizując korelację wzajemną sygnału wejściowego i wyjściowego?
9) Szumem białym ξ[n] = w[n] o zerowej wartości średniej i wariancji σw2 pobudzono
filtr cyfrowy o transmitancji
1
, 0<a<1
(5.59)
H(z) =
1 − az −1
7
Czyli połączenie “szeregowe” – wyjście pierwszego podłączone jest do wejścia drugiego filtru.
2014-11-23 1:11 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 21
Rys. 5.5: Poglądowe przedstawienie macierzy z wieloma realizacjami sygnałów
a) Wyznaczyć i naszkicować widmo mocy sygnału wyjściowego η[n].
b) Wyznaczyć funkcję autokowariancji sygnału wyjściowego.
c) Wyznaczyć wzajemne widmo mocy sygnału ξ[n] i η[n].
10) Wyznaczyć czasową funkcję autokorelacji sygnału x1 [n] = 1[n]−1[n−5] oraz sygnału
x2 [n] = 1[n − 10] − 1[n − 15]. Skorzystać z graficznej interpretacji splotu. Czy opóźnienie
sygnału wpływa na przebieg funkcji autokorelacji.
11) Filtr o transmitancji H(z) został pobudzony w chwili n = 0 stacjonarnym sygnałem
stochastycznym. Czy sygnał η[n] na wyjściu filtru jest stacjonarny dla n ­ 0.
5.3. Dostępny sprzęt i oprogramowanie
5.3.1. Skrypty MATLABa®
Wszystkie funkcje c5_**** zwracają macierz, której wiersze są realizacjami sygnałów losowych - patrz rys. 5.5.
Wyjątkiem jest funkcja do rejestracji sygnałów rzeczywistych GETDATA – zwraca ona
realizacje jako kolumny macierzy wynikowej.
Standardowe funkcje MATLABa®
Sygnały (pseudo)losowe w Matlabie generuje się korzystając z dwóch podstawowych funkcji:
» rr=rand(m,n);%sygnał o rozkładzie równomiernym na odcinku (0,1)
» rr=randn(m,n);%sygnał o rozkładzie normalnym (Gaussa)
W obu przypadkach wynikem jest macierz o rozmiarze m na n, wypełniona niezależnymi
próbkami danych losowych.
Wszystkie funkcje Matlaba, które zdefiniowane są dla argumentów wektorowych (filter,
std, mean i.t.d.), będą w przypadku argumentu macierzowego działać oddzielnie na każdej
22 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 2014-11-23 1:11
kolumnie macierzy. Można więc od razu wykonać obliczenia np. dla wielu realizacji sygnału
losowego, jeśli kolejne realizacje ustawimy w kolumnach8 .
Również polecenie plot(x,Y) wyświetli kolumny macierzy Y jako kolejne linie na jednym wykresie (o ile liczba wierszy macierzy Y jest równa długości wektora x – inaczej zgłosi
błąd).
5.3.2. Aparatura
Tu powinien znaleźć się opis generatora szumów analogowych; co prawda wykorzystujemy
tylko jedno gniazdo i tylko jedną funkcję …
5.4. Eksperymenty do wykonania w laboratorium – sygnały
losowe, ich analiza i przetwarzanie
5.4.1. Podstawy
5.4.1.1. Funkcja gęstości prawdopodobieństwa a momenty procesów losowych
Zanotuj
Wybierz z tabeli 5.1 i zanotuj parametry szumu wg. numeru stanowiska.
Tabela 5.1
Nr stan.
1
2
3
4
5
6
7
8
9
10
11
12
13
µ
+1
0.32
0.8
1
4
40
3.2
4.8
-1
-0.5
0
-5
1.41
σ2
0.16
0.32
0.08
2
4
10
32
0.8
64
10
96
49
2
Wygeneruj M = 10000 realizacji szumów o długości N = 100 próbek każda dla trzech
różnych rodzajów szumu – użyj funkcji c5_noise, której parametry wejściowe są objaśnione w poniższym przykładowym kodzie.
M=10000 %liczba realizacji
N=100
%długość realizacji
mu=.... %wartość średnia
sigma2=....% wariancja
%ostatni parametr wybiera rodzaj rozkładu p-stwa
A1 = c5_noise(M, N, mu, sigma2, 'gauss');
A2 = c5_noise(M, N, mu, sigma2, 'jednost');
A3 = c5_noise(M, N, mu, sigma2, 'dwupkt');
Odpowiedz
Dla każdego przypadku na pierwszym wykresie funkcja wyświetli przebieg czasowy
wybranej realizacji na tle kilku innych. Na kolejnym zobaczymy histogram obliczony ze
wszystkich M realizacji dla jednej z chwil czasowych oraz teoretyczną funkcję gęstości
(masy) prawdopodobieństwa.
Przeanalizuj wykresy. Odpowiedz na pytania:
– Czym różnią się powyższe sygnały stochastyczne?
8
Wynik funkcji C5_***** musimy więc przetransponować – do tego służy operator .'.
2014-11-23 1:11 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 23
– Czy znajomość momentów daje pełną wiedzę o sygnale stochastycznym?
– Jakie pojęcie opisujące sygnał stochastyczny może być przybliżone histogramem obliczonym po realizacjach? Pod jakim warunkiem?
5.4.1.2. Stacjonarność procesów losowych
Za pomocą funkcji c5_station wygeneruj M = 1000 realizacji szumu o długości N =
100 próbek każda dla różnych rodzajów szumu. Funkcja c5_station generuje przykłady
sygnałów losowych o róznych właściwościach czasowych.
A1 = c5_station(M, N, 'stat');
A2 = c5_station(M, N, 'varmean');
A3 = c5_station(M, N, 'varvar');
Dla każdego przypadku funkcja na górnym wykresie wyświetli przebieg czasowy wybranej realizacji a na dolnym nałożone na siebie wszystkie realizacje (punktami).
Odpowiedz na pytanie: (dla każdego przypadku) Czy dany sygnał jest, Twoim zdaniem9 ,
stacjonarny/niestacjonarny? Co o tym świadczy? Czy mając daną tylko jedną realizację
łatwo to określić?
Odpowiedz
5.4.1.3. Ergodyczność procesów losowych
Za pomocą funkcji c5_noise wygeneruj M = 2000 realizacji szumu gaussowskiego o
długości N = 2000 próbek każda. Użyj tych samych parametrów szumu, co w zadaniu
5.4.1.1 (tj. wg tabeli).
Korzystając z funkcji mean() oraz var() i odpowiedniego indeksowania macierzy z szumami oblicz średnią i wariancję
– dla chwili n = 0 po wszystkich realizacjach
– dla pierwszej realizacji po czasie
Wskazówka: Aby poprawnie zaindeksować macierz, przyjrzyj się rysunkowi rys. 5.5;
przypomnij sobie, że w Matlabie pierwszy (licząc od 1) wiersz macierzy A to A(1,:), a
pierwsza kolumna to A(:,1).
Odpowiedz na pytania:
– Jaki wniosek można wysnuć co do ergodyczności tego konkretnego sygnału?
– Czy mając tylko jedną realizację (jak to ma najczęściej miejsce w praktyce) a nie wiele
(jak w tym ćwiczeniu) łatwo uzasadnić założenie o ergodyczności?
5.4.1.4. Estymacja funkcji autokorelacji i widma gęstości mocy
W podpunkcie tym i kolejnych założymy, że badane sygnały są stacjonarne i ergodyczne. Dlatego estymaty autokorelacji i widma gęstości mocy będą obliczane po czasie a nie po realizacjach. Większa liczba realizacji posłuży do tego aby zbadać jak estymaty zmieniają się pomiędzy realizacjami na bazie których zostały obliczone.
9
W zagadnieniach dotyczących sygnałów losowych zawsze musimy być ostrożni z formułowaniem ostrej
opinii: nigdy nie mówimy “czarne”/”białe” – tylko “wygląda jak czarne”, “nie widzę cech, które wskazywałyby
że jest białe” – bo naszą opinię formułujemy na podstawie skończonej liczby realizacji. Tak samo nieostro (ale z
innych przyczyn) odbywa się to w reklamie: “Prawdopodobnie najlepsze piwo na świecie.”.
Odpowiedz
24 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 2014-11-23 1:11
Rys. 5.6: Rejestracja sygnału z generatora szumów
Badać będziemy sygnał z generatora szumów dostepnego jako wkładka w kasecie laboratoryjnej. Szum na wyjściu generatora jest odpowiednio wzmocnionym szumem diody półprzewodnikowej i w zakresie analizowanym w laboratorium wykazuje cechy gaussowskiego
szumu białego.
Zanotuj
Odpowiedz
Odpowiedz
Zestaw układ pomiarowy jak na rys. 5.6. Ustaw potencjometr mocy szumu w połowie zakresu.
Zarejestruj M = 100 realizacji szumu, o długości N = 1000 próbek każda, przy czestotliwości próbkowania 48 kHz.
» A=GETDATA(N,M,1/48000);% W macierzy A realizacje są kolumnami!
Oblicz moc każdej realizacji i wykreśl ją w funkcji numeru realizacji.
Wskazówka: Funkcja var(A) domyślnie obliczy wariancję każdej kolumny macierzy.
Oblicz i zanotuj uśrednioną po realizacjach wartość mocy, przeliczoną na decybele.
Następnie za pomocą funkcji c5_xcorr oblicz i wyświetl autokorelację dla wszystkich realizacji. Funkcja c5_xcorr oblicza autokorelację (zgodnie ze wzorem (5.18)), i wyswietla
wynik dla pierwszej realizacji na tle pozostałych wyników.
» R=c5_xcorr(A.');% po transpozycji realizacje są już wierszami
Odpowiedz na pytania:
– Czym różnią się otrzymane estymaty autokorelacji od przebiegu teoretycznego?
– Przy pomocy jakiego pojęcia matematycznego można opisać wielkość rozrzutów wartości estymowanej autokorelacji z róznych realizacji?
– Przy pomocy jakiego pojęcia matematycznego można opisać rozbieżność wartości estymowanej autokorelacji od wartości prawdziwej autokorelacji?
– Jak się ma wartość autokorelacji dla przesunięcia m = 0 do zmierzonej wariancji (mocy)
sygnału?
Za pomocą funkcji c5_xcorr2spec przekształć estymatę autokorelacji w estymatę widma mocy (zgodnie ze wzorem (5.19)).
» S=c5_xcorr2spec(R);
Odpowiedz na pytania:
– Czym różnią się otrzymane estymaty widma gęstości mocy od przebiegu teoretycznego?
– Jak na podstawie otrzymanego widma, korzystając z Tw. Parsevala ((5.56)), można wy-
2014-11-23 1:11 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 25
znaczyć moc (wariancję) sygnału?
5.4.1.5. Ekstra Estymacja funkcji autokorelacji i widma gęstości mocy (II)
Powtórz eksperymenty z poprzedniego zadania z sygnałem symulowanym (c5_noise) i porównaj wyniki.
5.4.2. Periodogram
5.4.2.1. Wpływ długości periodogramu na estymatę widma mocy
Dla M = 100 realizacji i N = 100, 1000, 10000 za pomocą funkcji c5_noise_sin
wygeneruj realizacje sygnałów będących sumą szumu gaussowskiego o zerowej średniej i
dwóch sinusoid o bliskich i możliwe niecałkowitoliczbowych pulsacjach np 1.037*[0.103
0.106] a następnie funkcją c5_per oblicz i wyświetl periodogramy tych sygnałów.
Zanotuj wybrane częstotliwości.
Parametry funkcji c5_noise_sin są identyczne z parametrami funkcji c5_noise;
dodatkowy, szósty parametr to wektor określający pulsacje dodanych sinusoid.
Funkcja c5_per(A) oblicza pojedyńczy periodogram (bez podziału na segmenty) z
każdego wiersza macierzy A i wyświetla wszystkie obliczone periodogramy w skali logarytmicznej (opcjonalny drugi argument: 'lin' włącza skalę liniową, 'noplot' wyłącza
rysowanie całkowicie).
Zanotuj
M = 100;
N = 100;
A = c5_noise_sin(M, N, 0, 1, 'gauss', 1.037*[0.103, 0.106]);
S_per = c5_per( A );
Na podstawie wykresów dla każdego przypadku (N = 100, 1000, 10000) zanotuj czy Zanotuj
udało się rozróżnić składowe sinusoidalne.
Powtórz eksperyment z wyłączonym wyświetlaniem ('noplot' w wywołaniu funkcji c5_per),
dla M = 10000 realizacji.
» M=10000;
» S_per = c5_per( A, 'noplot' );
Dla każdego N za pomocą funkcji var() i odpowiedniego indeksowania macierzy S oszacuj wariancję estymaty widma S dla próbki odpowiadającej częstotliwości −fs /2.
Wskazówka: Wariancję estymaty oblicza się biorąc odpowiednią próbkę estymaty z
każdej dostępnej realizacji – uśredniając po realizacjach kwadrat odchylenia tych próbek
od średniej wartości tych próbek. Obliczenia (usunięcie średniej, uśrednienie kwadratów)
wykona na Twoje polecenie funkcja var(), a Ty tylko zadbaj, żeby robiła to wzdłuż właściwego wymiaru macierzy.
Odpowiedz
Odpowiedz na pytanie: Czy wariancja tej estymaty zależy od długości badanych realizacji N ?
5.4.2.2. Metody modyfikacji periodogramu
W części teoretycznej omówiono kilka metod poprawiających jakość periodogramu. W bieżącym podpunkcie zostanie zbadane jak dużą poprawę one przynoszą i jakim kosztem się to
dzieje.
26 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 2014-11-23 1:11
Wykorzystywana będzie funkcja c5_averp(A, L, M, win, disp) której parametry wejściowe mają następujące znaczenie
A
– macierz realizacji sygnału losowego;
L
– długość jednego segmentu;
M
– liczba próbek wspólnych dla nakładających się segmentów (0 – bez nakładania)
win – typ okna (nazwa funkcji Matlaba wywoływanej do utworzenia okna, np. 'rectwin'
albo 'hamming')
disp – sposób wyświetlania ('db', 'noplot', 'lin')
Najpierw, jak w poprzednim podpunkcie, wygeneruj M = 100 realizacji szumu z dodanymi
sinusoidami o długości N = 1000 za pomocą funkcji c5_noise_sin.
Następnie oszacuj eksperymentalnie rozróżnialność częstotliwościową periodogramów (np.
na podstawie szerokości prążka od składowej sinusoidalnej) dla następujących wariantów
estymatora widma mocy:
– bez uśredniania (L=size(A,2)), bez nakładania segmentów, okno prostokątne
– uśrednianie z segmentów o długości 100, bez nakładania segmentów, okno prostokątne
– uśrednianie z segmentów o długości 100, nakładanie co pół segmentu, okno prostokątne
– bez uśredniania, bez nakładania segmentów, okno Hamminga
– uśrednianie z segmentów o długości 100, bez nakładania segmentów, okno Hamminga
– uśrednianie z segmentów o długości 100, nakładanie co pół segmentu, okno Hamminga
Przykładowe wywołanie funkcji wyświetlającej periodogram dla ostatniego przypadku to:
c5_averp( A, 100, 50, 'hamming', 'db');
Zanotuj
Zanotuj oszacowaną z wykresu rozróznialność dla każdego z powyższych przypadków
(tj. dla każdego wariantu estymatora widma mocy). Zostaw miejsce na dopisanie wariancji,
które zbadasz w następnym eksperymencie.
Wygeneruj taki sam sygnał jak poprzednio, tyle, że w M = 10000 realizacjach. Dla każdego z badanych wariantów estymatora widma mocy użyj funkcji c5_averp z parametrem
'noplot'
S=c5_averp( A, 100, 50, 'hamming', 'noplot');
Zanotuj
Odpowiedz
aby otrzymać macierz periodogramów. Dla każdego przypadku za pomocą funkcji var i
odpowiedniego indeksowania macierzy S oszacuj wariancję estymaty widma S (po realizacjach) dla próbki odpowiadającej częstotliwości −fs /2.
Zanotuj oszacowane wariancje.
Odpowiedz na pytanie: Jak poznane metody modyfikacji periodogramów wpływają na
wariancję oraz rozróżnialność częstotliwościową?
5.4.3. Zadania praktyczne – miniprojekty
5.4.3.1. Testowanie filtru szumem
Skonstruuj filtr SOI o losowych współczynnikach; dla zachowania pozorów, że wiemy co
robimy, dopilnuj, żeby był to filtr o stałym opóźnieniu grupowym
» B=2*rand(1,6)-1;%losowanie 6 liczb pomiędzy -1 a +1
» B=[B B(end:-1:1)]%symetria da nam liniową fazę
» plot(filter(B,1,[1 zeros(1,30)]));
2014-11-23 1:11 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 27
» title('Odpowiedz impulsowa filtru')
Odpowiedz na pytanie: Czy powyższe czynności dały filtr o stałym opóźnieniu grupowym? Odpowiedz
Uzasadnij. (Nie sprawdzaj eksperymentalnie, tylko przypomnij sobie teorię).
Zaprojektuj i wykonaj prosty eksperyment, którego wynikiem będzie charakterystyka amlitudowa filtru. Postępuj według schematu jak poniżej, wykorzystując pojecie periodogramu i funkcje używane w cwiczeniu. Zanotuj swoje decyzje projektowe (np. wybraną dłu- Zanotuj
gość realizacji szumu, parametry obliczania periodogramu) i naszkicuj
periodogramy, które
✿✿✿✿✿✿✿✿✿
obliczyłeś(–aś) oraz znalezioną charakterystykę.
Naszkicuj
Schemat postępowania:
Chwilowo c5_noise nie lubi rysować wykresu dla jednej realizacji
– Wygeneruj szum (ciąg pseudolosowy)
razi, to użyj szóstego argumentu 'noplot'.
– Sprawdź jego widmową gestość mocy
– Przefiltruj testowanym filtrem
– Odrzuć część próbek z początku („stan nieustalony”) – skróć sygnał
– Oblicz widmową gęstość mocy
– Oblicz charakterystykę amplitudową badanego filtru
– Na koniec użyj
» freqz(B,1);
i porównaj wynik z Twoim wynikiem (np. nanieś na ten sam wykres).
5.4.3.2. Extra Testowanie filtru szumem kolorowym
Powtórz powyższe zadanie, używając bardziej realistycznych warunków, tj. zniekształcając
widmo mocy szumu (korelując go wewnętrznie) przed użyciem go do testowania. Jeśli Twoja
fantazja nie podpowiada Ci ciekawszego sposobu, zniekształć szum np. filtrem SOI o współczynnikach [-1 1].
5.4.3.3. Widmo hałasu w laboratorium
Zarejestruj kilkanaście-kilkadziesiąt sekund hałasu panującego w laboratorium (lub, do wyboru, szum konkretnej aparatury albo sygnał z radia ustawionego przypadkowo).
Oblicz periodogram, dobierając jego parametry dla otrzymania wyraźnego wykresu. Naszkicuj
Naszkicuj
✿✿✿✿✿✿✿✿✿
periodogram, próbując objaśnić widoczne na nim piki widma mocy.
Przedyskutuj z kolegą lub z prowadzącym skąd mogą pochodzić widoczne na periodogramie częstotliwości.
5.4.3.4. Extra Funkcja autokorelacji sygnału OFDM albo DAB
Zadanie wymaga dostępności odbiornika cyfrowego USB i zainstalowanych odpowiednich
sterowników10 .
Odbiornik cyfrowy USB z układem Realtek RTL2832U umozliwia zarejestrowanie sygnału radiowego w postaci 8-bitowych próbek zespolonych sygnału przeniesionego do pasma
podstawowego.
10
Potrzebne są sterowniki sdr-rtl, którymi trzeba zastąpić oryginalne sterowniki Windows'owe. Pod systemem Linux trzeba usunąć sterownik domyślny rmmod dvb_usb_rtl28xxu.
28 Analiza i przetwarzanie sygnałów stochastycznych (periodogram, filtracja szumów) 2014-11-23 1:11
Zainstaluj odbiornik cyfrowy w porcie USB, dołącz antenę. Uruchom program SDR#11 i
znajdź sygnał telewizji cyfrowej – zanotuj częstotliwości graniczne pasma sygnału. W Warszawie powinieneś znaleźć sygnał multipleksu TVP na częstotliwosci środkowej 522MHz.
Możesz też zainteresować się sygnałem radia cyfrowego (DAB) – w Warszawie powinien się on dać znaleźć na częstotliwości środkowej 183.648 MHz.
Zarejestruj fragment sygnału OFDM telewizji cyfrowej (użyj odbiornika USB). Niestety
będzie to dwumegahertzowy fragment całego pasma zajmującego 7 MHz.
Wyłącz SDR# i zarejestruj próbki sygnału radiowego, wywołując z terminala
rtl_sdr -f522000000 -n20000 <nazwapliku>
(podano przykład rejestracji 20000 próbek na częstotliwości 522 MHz)
Sprawdź, czy plik powstał i ma rozsądną długość.
Wczytaj dane do Matlab'a
» f=fopen(<nazwapliku>);
» xxx=fread(f,[2,Inf],'int8');%przeczytaj dane do macierzy dwa wiersz
» fclose(f);
» xxc=xxx(1,:)+j*xxx(2,;); %uzyskaj sygnał zespolony
Oblicz i wyświetl funkcję autokorelacji sygnału. Naszkicuj ją i spróbuj zrozumieć co w niej
widać.
11
W systemie Linux odpowiednikiem będzie program gqrx.